第三章 投影与视图章末检测题(基础练含解析)
文档属性
| 名称 | 第三章 投影与视图章末检测题(基础练含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 419.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 09:48:05 | ||
图片预览



文档简介
初中数学湘教版九年级下册第三章 投影与视图 章末检测(基础练)
一、单选题
1.下列光线所形成投影是平行投影的是(?? )
A.?太阳光线???????????????????????B.?台灯的光线???????????????????????C.?手电筒的光线???????????????????????D.?路灯的光线
2.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( ???)
A.?小明的影子比小强的影子长????????????????????????????????B.?小明的影子比小强的影子短
C.?小明的影子和小强的影子一样长?????????????????????????D.?两人的影子长度不确定
3.如图是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是(??? )
A.?①②③④???????????????????????????B.?④③①②???????????????????????????C.?④①③②???????????????????????????D.?②①③④
4.矩形木框在阳光照射下,在地面上的影子不可能是( ??)
A.???????????????????B.???????????????????C.???????????????????D.?
5.下列几何体中,属于棱柱的是(??? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
6.三棱锥有(? )个面
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
7.圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是(?? )
A.?53 cm??????????????????????????????????B.?10cm??????????????????????????????????C.?6cm??????????????????????????????????D.?5cm?
8.已知圆锥底面圆的半径为3,母线长为4,则这个圆锥的侧面积是(?? )
A.?4 π????????????????????????????????????B.?9 π????????????????????????????????????C.?12 π????????????????????????????????????D.?16 π ???
9.一个圆锥的底面半径为10,母线长30,则它的侧面展开图(扇形)的圆心角是(??? )
A.?60°?????????????????????????????????????B.?90°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
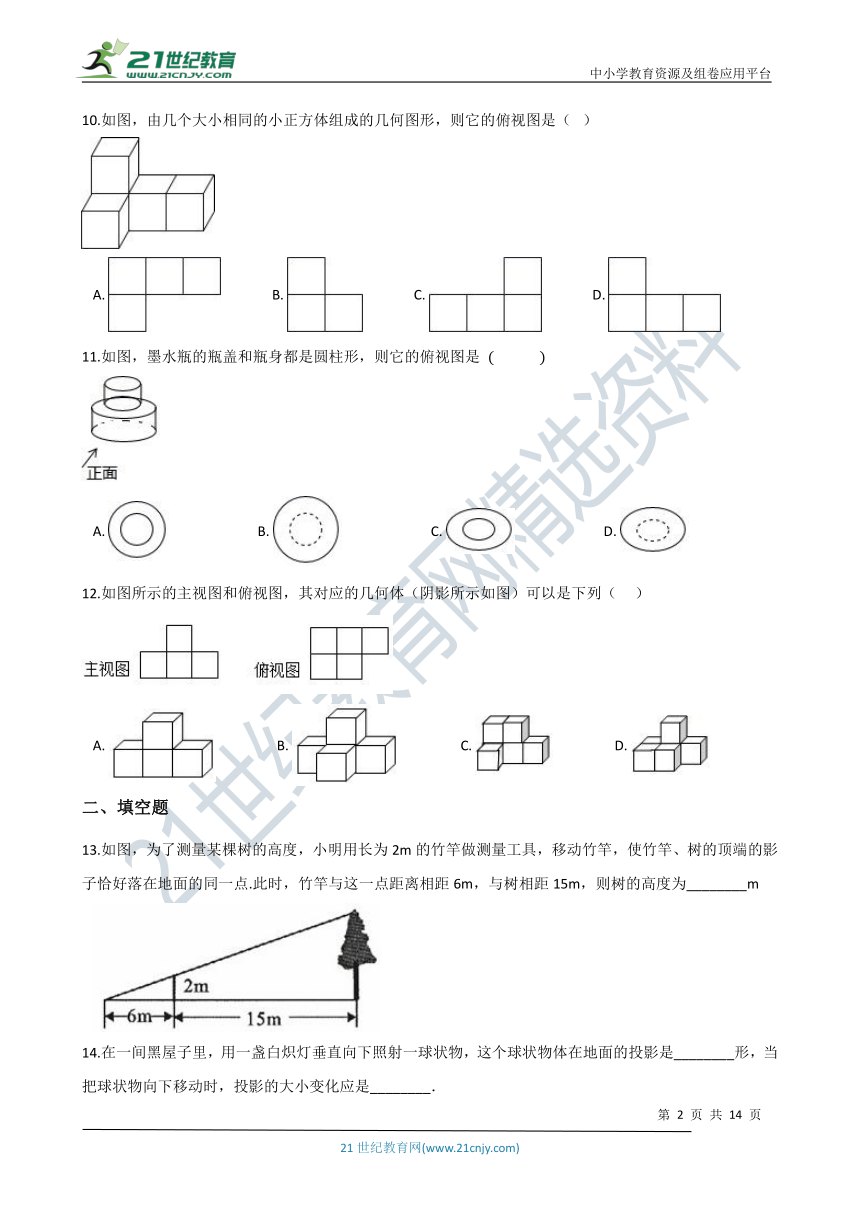
10.如图,由几个大小相同的小正方体组成的几何图形,则它的俯视图是(? )
A.????????????????B.????????????????C.????????????????D.?
11.如图,墨水瓶的瓶盖和瓶身都是圆柱形,则它的俯视图是 ( )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
12.如图所示的主视图和俯视图,其对应的几何体(阴影所示如图)可以是下列(??? )
A.???????????????????B.???????????????????C.???????????????????D.?
二、填空题
13.如图,为了测量某棵树的高度,小明用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度为________m
?
14.在一间黑屋子里,用一盏白炽灯垂直向下照射一球状物,这个球状物体在地面的投影是________形,当把球状物向下移动时,投影的大小变化应是________.
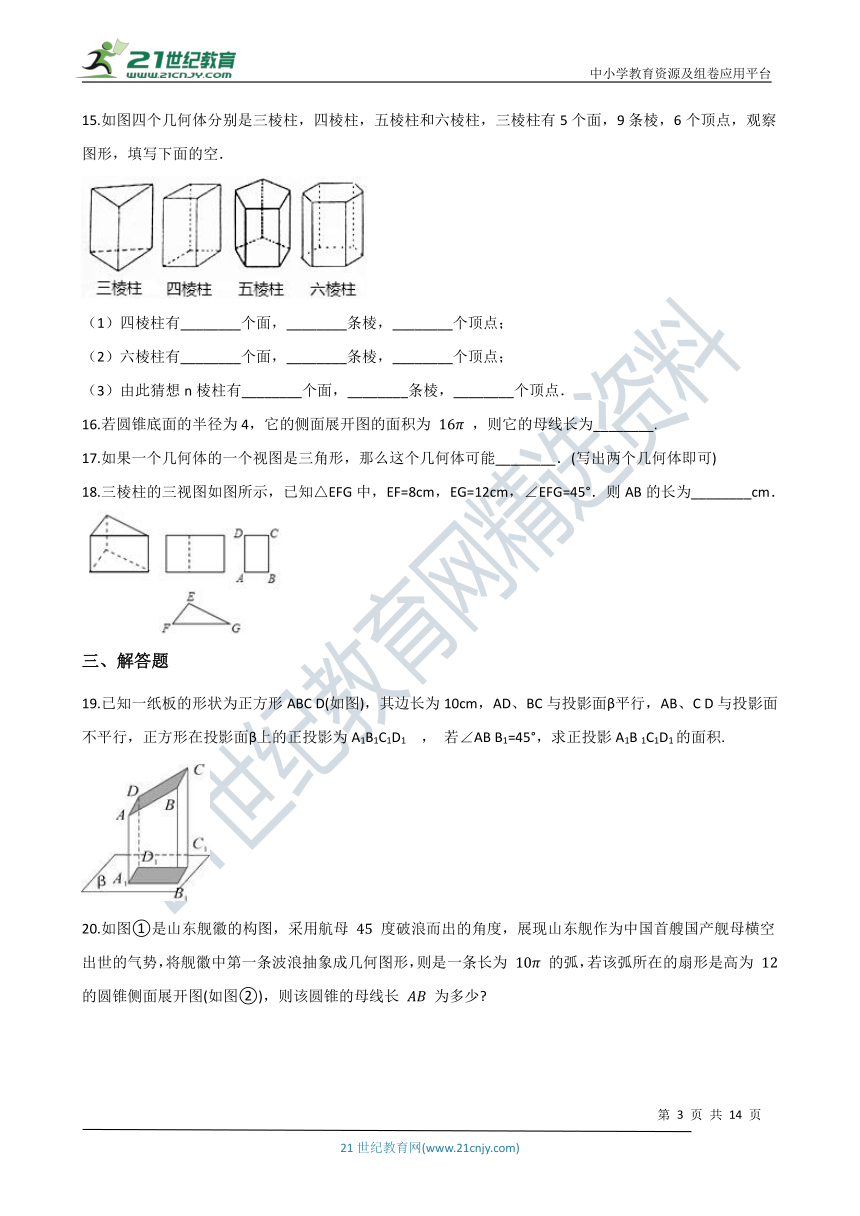
15.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有________个面,________条棱,________个顶点;
(2)六棱柱有________个面,________条棱,________个顶点;
(3)由此猜想n棱柱有________个面,________条棱,________个顶点.
16.若圆锥底面的半径为4,它的侧面展开图的面积为 16π ,则它的母线长为________.
17.如果一个几何体的一个视图是三角形,那么这个几何体可能________.(写出两个几何体即可)
18.三棱柱的三视图如图所示,已知△EFG中,EF=8cm,EG=12cm,∠EFG=45°.则AB的长为________cm.
三、解答题
19.已知一纸板的形状为正方形ABC D(如图),其边长为10cm,AD、BC与投影面β平行,AB、C D与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1 , 若∠AB B1=45°,求正投影A1B 1C1D1的面积.
20.如图①是山东舰徽的构图,采用航母 45 度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 10π 的弧,若该弧所在的扇形是高为 12 的圆锥侧面展开图(如图②),则该圆锥的母线长 AB 为多少?
21.作图题: 如图所示:大王站在墙前,小明站在墙后,小明不能让大王看见,请你画出小明的活动区域.
22.如图,是由一些大小相同的小正方体组合成的简单几何体.
(1)图中有________块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.(注意:三视图画好后请打上阴影)
23.已知一个六棱柱,它的底面边长都是5厘米,侧棱长都是8厘米,请回答下列问题。
(1)这个六棱柱一共有多少个面?一共有多少条棱?这些棱的长度之和是多少?
(2)沿一条侧棱将这个六棱柱侧面全部展开成一个平面图形,这个图形的面积是多少?
24.已知三棱柱、四棱柱和五棱柱的顶点数、棱和面数之间的关系如下表所示。请你完成下列问题:
名称
顶点(个)
棱(条)
面(个)
三棱柱
6
9
5
四棱柱
8
12
6
五棱柱
10
15
7
六棱柱
……
……
……
……
(1)请你把六棱柱的顶点数,棱数和面数填在上表中;
(2)请你根据表中反映的规律,写出十五棱柱的顶点数+棱数-面数=________。
25.如图,甲、乙两个几何体是由一些棱长是1的正方体粘连在一起所构成的,这两个几何体从上面看到的形状图相同是“ ”请回答下列问题:
(1)请分别写出粘连甲、乙两个几何体的正方体的个数.
(2)甲、乙两个几何体从正面、左面、上面三个方向所看到的形状图中哪个不相同?请画出这个不同的形状图.
(3)请分别求出甲、乙两个几何体的表面积.
26.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,并写出D点坐标为;
(2)连接AD、CD,求 圆 D的半径(结果保留根号)及扇形ADC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径(结果保留根号).
答案解析部分
一、单选题
1. A
考点:平行投影
解:四个选项中只有太阳光是平行光线;故太阳光线下形成的投影是平行投影.
故答案选A.
分析:判断投影是平行投影的方法是看光线是否是平行的,如果光线是平行的,所得到的投影就是平行投影.
2. D
考点:中心投影
解:在同一路灯下由于位置不同,影长也不同,所以无法判断谁的影子长.
故答案为:D.
分析:在同一路灯下由于位置不确定,根据中心投影的特点判断得出答案即可.
3. B
考点:平行投影
解:根据平行投影的特点以及北半球影长的规律可知:从早晨到傍晚物体的指向是:西-西北-北-东北-东,影长由长变短,再变长.可知先后顺序是④③①②.
故答案为:B.
分析:根据平行投影的特点以及北半球影长的规律可知:从早晨到傍晚物体的指向是:西-西北-北-东北-东,影长由长变短,再变长,据此判断即可.
4. C
考点:平行投影
解:矩形木框再阳光的照射下形成的投影是平行四边形或一条线段,即相对的边平行或重合
故A不可能,不会是梯形
故答案为:C
分析:在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析即可。
5. C
考点:棱柱及其特点
解:①棱柱;②圆柱;③棱柱;④棱锥;⑤圆锥;⑥棱柱.
故答案为:C.
分析:根据棱柱的特点逐个判断即可。
6. B
考点:棱柱及其特点
解:∵三棱锥有三个侧面和一个底面,
∴三棱锥共有4个面.
故答案为:B.
分析:根据三棱锥的图形可知三棱锥有三个侧面和一个底面共4个面。
7. A
考点:圆锥的计算
解:设圆锥的母线长为R,
根据题意得:2π·5=180πR180 ,
解得R=10,
圆锥的高=102-52=53;
故答案为:A.
分析: 设圆锥的母线长为R,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2π?5=180πR180 , 然后解方程即可母线长,然后利用勾股定理求得圆锥的高即可.
8. C
考点:圆锥的计算
解:圆锥底面的周长=2π×3=6π,
∴侧面积=12×6π×4=12π;
故答案为:C.
分析:先求出圆锥的地面的周长c,再根据公式:侧面积=12×底面周长×母线长即可求解.
9. C
考点:圆锥的计算
解:由题意可知圆锥的底面周长为20π,即圆锥侧面展开图扇形的弧长为20π,圆锥的母线长为30,
即圆锥侧面展开图扇形的半径为30,
由弧长公式l=nπr180° , 将l=20π,r=30代入弧长公式中求得n=120°。
故答案为:C
分析:此题主要考查圆锥的计算,由圆锥的侧面展开图为扇形可知圆锥的底面周长为扇形的弧长,圆锥的母线长为扇形的半径,根据弧长公式即可求得扇形的圆心角度数。
10. A
考点:简单几何体的三视图
解:根据观察知它的俯视图是下面一行靠左一个小正方形,上面一行有3个小正方形.
故答案为:A.
分析:直接从上面观察这个立体图形,即可得到.俯视图.
11. A
考点:简单组合体的三视图
解:墨水瓶的瓶盖和瓶身都是圆柱形,则它的俯视图是: .
故答案为:A.
分析:直接利用俯视图即从物体的上面往下看,进而得出视图.
12. D
考点:由三视图判断几何体
解:A、B、D选项的主视图符合题意;
C选项的主视图和俯视图都不符合题意,
D选项的俯视图符合题意,
综上:对应的几何体为D选项中的几何体.
故答案为:D.
分析:根据几何体的主视图确定A、B、C选项,然后根据俯视图确定D选项即.
二、填空题
13. 7
考点:平行投影
解:设树的高度为 x m,由相似可得 x2=6+156=72 ,解得 x=7 ,所以树的高度为7m
分析:本本题利用平行线分线段成比例即可解答。找到对应边,列出等式解答即可。
14. 圆;变小
考点:中心投影
解:用一盏白炽灯垂直向下照射一球状物,这个球状物体在地面的投影是 圆形,当把球状物向下移动时,投影的大小变化应是 变小.
故答案为:(1)圆;(2)变小
分析:根据中心投影的性质得出:等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短,根据性质即可得出答案。
15. (1)6;12;8
(2)8;18;12
(3)(n+2);3n;2n
考点:棱柱及其特点
解:(1)四棱柱有6个面,12条棱,8个顶点;(2)六棱柱有8个面,18条棱,12个顶点;(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为(1)6,12,8;(2)8,18,12;(3) (n+2),3n,2n.
分析:结合已知三棱柱、四棱柱、五棱柱和六棱柱的特点,可知 n 棱柱一定有 (n+2) 个面, 3n 条棱和 2n 个顶点.
16. 4
考点:圆锥的计算
解:设圆锥的母线长为l,
根据题意得 12 ?2π?4?l=16π,
解得l=4π,
即圆锥的母线长为4.
故答案为:4.
分析:设圆锥的母线长为l,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得到 12 ?2π?4?l=16π,然后解方程即可.
17. 圆锥、三棱柱、三棱锥等
考点:由三视图判断几何体
解:三视图中有一个图是三角形,这个几何体可能是圆锥,三棱柱,三棱锥等.
分析:根据几何体的一个视图是三角形,结合几何体的特征即得结论.
18. 42
考点:简单几何体的三视图
解:如图,过E作ED⊥FG,
∵EF=8cm,∠EFG=45°,
∴FD=EF×cos45°=8×22=42。
故答案为:42。
分析:由视图可知,AB长即为DF长。
三、解答题
19. 解:过A作AE⊥BB1 , 交于点E,
因为∠ABB1=45°,
所以AE=BE=22AB=52cm
因为四边形ABCD是正方形,AD、BC与投影面β平行,
所以A1D1=B1C1=AD=BC=10cm,
所以正投影A1B 1C1D1的面积=10×52=502(cm2)
考点:平行投影
分析:AD、BC与投影面β平行,则A1D1=B1C1=AD=BC,而且四边形ABCD是正方形,可得正投影A1B 1C1D1是正方形,求出A1B1的长即可(根据∠ABB1=45°可求得)。
20. 解: ∵ 圆锥底面周长 = 侧面展开后扇形的弧长 =10π,
∴OB=10π2π=5
在 RtΔAOB 中, AB=AO2+BO2=122+52=13 ,
所以该圆锥的母线长 AB 为 13 .
考点:圆锥的计算
分析:先利用扇形的弧长和圆锥底面的周长列方程求出OB的长,再利用勾股定理求出OB的长。
21. 解:如图,小明的活动区域是A、B、C三个阴影部分区域.
考点:中心投影
分析:根据题意,分别将大王所在的点与墙的两侧作连线,将其延长即可得到活动区域。
22. (1)11
(2)解:如图所示:
?.
考点:简单组合体的三视图
解:(1)根据如图所示即可数出有11块小正方体;
故答案为:11;
分析:(1)根据如图所示即可得出图中小正方体的个数;
(2)读图可得,左视图有2列,每列小正方形数目分别为2,2;俯视图有4列,每行小正方形数目分别为2,2,1,1.
23. (1)解:这个六棱柱一共有2+6=8个面
共有6×3=18条棱;
这些棱的长度之和是8×6+5×6×2=108厘米
(2)解:侧面全部展开成一个平面图形,其面积为8×5×6=240厘米2
考点:棱柱及其特点
分析:(1)六棱柱的面包括6个侧面和2个底面,共8个面;棱长包括侧面公共棱6条和每个底面棱长有6条,共18条棱。
(2)
24. (1)解:三棱柱:顶点个数=2×3,棱的条数=3×3,面的个数=3+2;
四棱柱:顶点个数=2×4,棱的条数=3×4,面的个数=4+2;
五棱柱:顶点个数=2×5,棱的条数=3×5,面的个数=5+2;
六棱柱:顶点个数=2×6=12,棱的条数=3×6=18,面的个数=6+2=8;
……
n棱柱:顶点个数=2n,棱的条数=3n,面的个数=n+2;
(2)解:十五棱柱:顶点个数=2×15=30,棱的条数=3×15=45,面的个数=15+2=17; 30+45﹣17=58.
考点:探索图形规律,棱柱及其特点
分析:(1)根据三棱柱、四棱柱、五棱柱,找出规律,写出n棱柱的公式,将n=6代入,填表即可。
(2)将n=15代入,求解顶点个数、楞数和面数。
25. (1)解:如图所示:甲的正方体有4+4=8个;乙的正方体有4+3=7个;
(2)解:甲、乙两个几何体的主视图相同,俯视图也相同,只有左视图不同;
甲、乙两个几何体的左视图不同,如图所示:
;
(3)解:甲几何体的表面积为:14+14=28;
乙几何体的表面积为:14+1+5+8=28.
考点:几何体的表面积,简单组合体的三视图,作图﹣三视图
分析:(1)分别利用几何的形状得出组成的个数;(2)甲的左视图从左往右3列正方形的个数依次为2,2,2;乙的左视图从左往右3列正方形的个数依次为2,1,2;(3)直接利用几何体的形状进而得出表面积.
26. (1)解:
点D的坐标为(2,0)
(2)解:半径=OA2+OD2=42+22=20=25
∵OD=CE=2,OA=DE=4,∠AOD=∠CEO=90? ,
∴△AOD≌△CDE,
∴∠OAD=∠CDE,
∴∠ADO+∠CDE=∠ADO+∠OAD=90? ,
∴∠ADC=90?.
∴扇形DAC的圆心角度数为90?;
(3)解:设圆锥的底面半径是r,
则2πr=90π×25180
∴r=52
即该圆锥的底面半径为52.
考点:确定圆的条件,圆锥的计算
分析:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,从而作出弦AB,BC的垂直平分线,交点即为圆心D;
(2)根据方格纸的特点由勾股定理即可算出该圆的半径,连接DA,DC,根据SAS得到两个三角形全等△AOD≌△DCE,根据全等三角形的对应角相等得出∠OAD=∠CDE,根据直角三角形的两锐角互余及等量代换平角的定义即可得出∠ADC=90°,即扇形的圆心角是90°;
(3)根据圆锥的底面周长等于弧长,列出方程,求解即可。
一、单选题
1.下列光线所形成投影是平行投影的是(?? )
A.?太阳光线???????????????????????B.?台灯的光线???????????????????????C.?手电筒的光线???????????????????????D.?路灯的光线
2.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( ???)
A.?小明的影子比小强的影子长????????????????????????????????B.?小明的影子比小强的影子短
C.?小明的影子和小强的影子一样长?????????????????????????D.?两人的影子长度不确定
3.如图是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是(??? )
A.?①②③④???????????????????????????B.?④③①②???????????????????????????C.?④①③②???????????????????????????D.?②①③④
4.矩形木框在阳光照射下,在地面上的影子不可能是( ??)
A.???????????????????B.???????????????????C.???????????????????D.?
5.下列几何体中,属于棱柱的是(??? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
6.三棱锥有(? )个面
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
7.圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是(?? )
A.?53 cm??????????????????????????????????B.?10cm??????????????????????????????????C.?6cm??????????????????????????????????D.?5cm?
8.已知圆锥底面圆的半径为3,母线长为4,则这个圆锥的侧面积是(?? )
A.?4 π????????????????????????????????????B.?9 π????????????????????????????????????C.?12 π????????????????????????????????????D.?16 π ???
9.一个圆锥的底面半径为10,母线长30,则它的侧面展开图(扇形)的圆心角是(??? )
A.?60°?????????????????????????????????????B.?90°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
10.如图,由几个大小相同的小正方体组成的几何图形,则它的俯视图是(? )
A.????????????????B.????????????????C.????????????????D.?
11.如图,墨水瓶的瓶盖和瓶身都是圆柱形,则它的俯视图是 ( )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
12.如图所示的主视图和俯视图,其对应的几何体(阴影所示如图)可以是下列(??? )
A.???????????????????B.???????????????????C.???????????????????D.?
二、填空题
13.如图,为了测量某棵树的高度,小明用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度为________m
?
14.在一间黑屋子里,用一盏白炽灯垂直向下照射一球状物,这个球状物体在地面的投影是________形,当把球状物向下移动时,投影的大小变化应是________.
15.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有________个面,________条棱,________个顶点;
(2)六棱柱有________个面,________条棱,________个顶点;
(3)由此猜想n棱柱有________个面,________条棱,________个顶点.
16.若圆锥底面的半径为4,它的侧面展开图的面积为 16π ,则它的母线长为________.
17.如果一个几何体的一个视图是三角形,那么这个几何体可能________.(写出两个几何体即可)
18.三棱柱的三视图如图所示,已知△EFG中,EF=8cm,EG=12cm,∠EFG=45°.则AB的长为________cm.
三、解答题
19.已知一纸板的形状为正方形ABC D(如图),其边长为10cm,AD、BC与投影面β平行,AB、C D与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1 , 若∠AB B1=45°,求正投影A1B 1C1D1的面积.
20.如图①是山东舰徽的构图,采用航母 45 度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 10π 的弧,若该弧所在的扇形是高为 12 的圆锥侧面展开图(如图②),则该圆锥的母线长 AB 为多少?
21.作图题: 如图所示:大王站在墙前,小明站在墙后,小明不能让大王看见,请你画出小明的活动区域.
22.如图,是由一些大小相同的小正方体组合成的简单几何体.
(1)图中有________块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.(注意:三视图画好后请打上阴影)
23.已知一个六棱柱,它的底面边长都是5厘米,侧棱长都是8厘米,请回答下列问题。
(1)这个六棱柱一共有多少个面?一共有多少条棱?这些棱的长度之和是多少?
(2)沿一条侧棱将这个六棱柱侧面全部展开成一个平面图形,这个图形的面积是多少?
24.已知三棱柱、四棱柱和五棱柱的顶点数、棱和面数之间的关系如下表所示。请你完成下列问题:
名称
顶点(个)
棱(条)
面(个)
三棱柱
6
9
5
四棱柱
8
12
6
五棱柱
10
15
7
六棱柱
……
……
……
……
(1)请你把六棱柱的顶点数,棱数和面数填在上表中;
(2)请你根据表中反映的规律,写出十五棱柱的顶点数+棱数-面数=________。
25.如图,甲、乙两个几何体是由一些棱长是1的正方体粘连在一起所构成的,这两个几何体从上面看到的形状图相同是“ ”请回答下列问题:
(1)请分别写出粘连甲、乙两个几何体的正方体的个数.
(2)甲、乙两个几何体从正面、左面、上面三个方向所看到的形状图中哪个不相同?请画出这个不同的形状图.
(3)请分别求出甲、乙两个几何体的表面积.
26.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,并写出D点坐标为;
(2)连接AD、CD,求 圆 D的半径(结果保留根号)及扇形ADC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径(结果保留根号).
答案解析部分
一、单选题
1. A
考点:平行投影
解:四个选项中只有太阳光是平行光线;故太阳光线下形成的投影是平行投影.
故答案选A.
分析:判断投影是平行投影的方法是看光线是否是平行的,如果光线是平行的,所得到的投影就是平行投影.
2. D
考点:中心投影
解:在同一路灯下由于位置不同,影长也不同,所以无法判断谁的影子长.
故答案为:D.
分析:在同一路灯下由于位置不确定,根据中心投影的特点判断得出答案即可.
3. B
考点:平行投影
解:根据平行投影的特点以及北半球影长的规律可知:从早晨到傍晚物体的指向是:西-西北-北-东北-东,影长由长变短,再变长.可知先后顺序是④③①②.
故答案为:B.
分析:根据平行投影的特点以及北半球影长的规律可知:从早晨到傍晚物体的指向是:西-西北-北-东北-东,影长由长变短,再变长,据此判断即可.
4. C
考点:平行投影
解:矩形木框再阳光的照射下形成的投影是平行四边形或一条线段,即相对的边平行或重合
故A不可能,不会是梯形
故答案为:C
分析:在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析即可。
5. C
考点:棱柱及其特点
解:①棱柱;②圆柱;③棱柱;④棱锥;⑤圆锥;⑥棱柱.
故答案为:C.
分析:根据棱柱的特点逐个判断即可。
6. B
考点:棱柱及其特点
解:∵三棱锥有三个侧面和一个底面,
∴三棱锥共有4个面.
故答案为:B.
分析:根据三棱锥的图形可知三棱锥有三个侧面和一个底面共4个面。
7. A
考点:圆锥的计算
解:设圆锥的母线长为R,
根据题意得:2π·5=180πR180 ,
解得R=10,
圆锥的高=102-52=53;
故答案为:A.
分析: 设圆锥的母线长为R,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2π?5=180πR180 , 然后解方程即可母线长,然后利用勾股定理求得圆锥的高即可.
8. C
考点:圆锥的计算
解:圆锥底面的周长=2π×3=6π,
∴侧面积=12×6π×4=12π;
故答案为:C.
分析:先求出圆锥的地面的周长c,再根据公式:侧面积=12×底面周长×母线长即可求解.
9. C
考点:圆锥的计算
解:由题意可知圆锥的底面周长为20π,即圆锥侧面展开图扇形的弧长为20π,圆锥的母线长为30,
即圆锥侧面展开图扇形的半径为30,
由弧长公式l=nπr180° , 将l=20π,r=30代入弧长公式中求得n=120°。
故答案为:C
分析:此题主要考查圆锥的计算,由圆锥的侧面展开图为扇形可知圆锥的底面周长为扇形的弧长,圆锥的母线长为扇形的半径,根据弧长公式即可求得扇形的圆心角度数。
10. A
考点:简单几何体的三视图
解:根据观察知它的俯视图是下面一行靠左一个小正方形,上面一行有3个小正方形.
故答案为:A.
分析:直接从上面观察这个立体图形,即可得到.俯视图.
11. A
考点:简单组合体的三视图
解:墨水瓶的瓶盖和瓶身都是圆柱形,则它的俯视图是: .
故答案为:A.
分析:直接利用俯视图即从物体的上面往下看,进而得出视图.
12. D
考点:由三视图判断几何体
解:A、B、D选项的主视图符合题意;
C选项的主视图和俯视图都不符合题意,
D选项的俯视图符合题意,
综上:对应的几何体为D选项中的几何体.
故答案为:D.
分析:根据几何体的主视图确定A、B、C选项,然后根据俯视图确定D选项即.
二、填空题
13. 7
考点:平行投影
解:设树的高度为 x m,由相似可得 x2=6+156=72 ,解得 x=7 ,所以树的高度为7m
分析:本本题利用平行线分线段成比例即可解答。找到对应边,列出等式解答即可。
14. 圆;变小
考点:中心投影
解:用一盏白炽灯垂直向下照射一球状物,这个球状物体在地面的投影是 圆形,当把球状物向下移动时,投影的大小变化应是 变小.
故答案为:(1)圆;(2)变小
分析:根据中心投影的性质得出:等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短,根据性质即可得出答案。
15. (1)6;12;8
(2)8;18;12
(3)(n+2);3n;2n
考点:棱柱及其特点
解:(1)四棱柱有6个面,12条棱,8个顶点;(2)六棱柱有8个面,18条棱,12个顶点;(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为(1)6,12,8;(2)8,18,12;(3) (n+2),3n,2n.
分析:结合已知三棱柱、四棱柱、五棱柱和六棱柱的特点,可知 n 棱柱一定有 (n+2) 个面, 3n 条棱和 2n 个顶点.
16. 4
考点:圆锥的计算
解:设圆锥的母线长为l,
根据题意得 12 ?2π?4?l=16π,
解得l=4π,
即圆锥的母线长为4.
故答案为:4.
分析:设圆锥的母线长为l,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得到 12 ?2π?4?l=16π,然后解方程即可.
17. 圆锥、三棱柱、三棱锥等
考点:由三视图判断几何体
解:三视图中有一个图是三角形,这个几何体可能是圆锥,三棱柱,三棱锥等.
分析:根据几何体的一个视图是三角形,结合几何体的特征即得结论.
18. 42
考点:简单几何体的三视图
解:如图,过E作ED⊥FG,
∵EF=8cm,∠EFG=45°,
∴FD=EF×cos45°=8×22=42。
故答案为:42。
分析:由视图可知,AB长即为DF长。
三、解答题
19. 解:过A作AE⊥BB1 , 交于点E,
因为∠ABB1=45°,
所以AE=BE=22AB=52cm
因为四边形ABCD是正方形,AD、BC与投影面β平行,
所以A1D1=B1C1=AD=BC=10cm,
所以正投影A1B 1C1D1的面积=10×52=502(cm2)
考点:平行投影
分析:AD、BC与投影面β平行,则A1D1=B1C1=AD=BC,而且四边形ABCD是正方形,可得正投影A1B 1C1D1是正方形,求出A1B1的长即可(根据∠ABB1=45°可求得)。
20. 解: ∵ 圆锥底面周长 = 侧面展开后扇形的弧长 =10π,
∴OB=10π2π=5
在 RtΔAOB 中, AB=AO2+BO2=122+52=13 ,
所以该圆锥的母线长 AB 为 13 .
考点:圆锥的计算
分析:先利用扇形的弧长和圆锥底面的周长列方程求出OB的长,再利用勾股定理求出OB的长。
21. 解:如图,小明的活动区域是A、B、C三个阴影部分区域.
考点:中心投影
分析:根据题意,分别将大王所在的点与墙的两侧作连线,将其延长即可得到活动区域。
22. (1)11
(2)解:如图所示:
?.
考点:简单组合体的三视图
解:(1)根据如图所示即可数出有11块小正方体;
故答案为:11;
分析:(1)根据如图所示即可得出图中小正方体的个数;
(2)读图可得,左视图有2列,每列小正方形数目分别为2,2;俯视图有4列,每行小正方形数目分别为2,2,1,1.
23. (1)解:这个六棱柱一共有2+6=8个面
共有6×3=18条棱;
这些棱的长度之和是8×6+5×6×2=108厘米
(2)解:侧面全部展开成一个平面图形,其面积为8×5×6=240厘米2
考点:棱柱及其特点
分析:(1)六棱柱的面包括6个侧面和2个底面,共8个面;棱长包括侧面公共棱6条和每个底面棱长有6条,共18条棱。
(2)
24. (1)解:三棱柱:顶点个数=2×3,棱的条数=3×3,面的个数=3+2;
四棱柱:顶点个数=2×4,棱的条数=3×4,面的个数=4+2;
五棱柱:顶点个数=2×5,棱的条数=3×5,面的个数=5+2;
六棱柱:顶点个数=2×6=12,棱的条数=3×6=18,面的个数=6+2=8;
……
n棱柱:顶点个数=2n,棱的条数=3n,面的个数=n+2;
(2)解:十五棱柱:顶点个数=2×15=30,棱的条数=3×15=45,面的个数=15+2=17; 30+45﹣17=58.
考点:探索图形规律,棱柱及其特点
分析:(1)根据三棱柱、四棱柱、五棱柱,找出规律,写出n棱柱的公式,将n=6代入,填表即可。
(2)将n=15代入,求解顶点个数、楞数和面数。
25. (1)解:如图所示:甲的正方体有4+4=8个;乙的正方体有4+3=7个;
(2)解:甲、乙两个几何体的主视图相同,俯视图也相同,只有左视图不同;
甲、乙两个几何体的左视图不同,如图所示:
;
(3)解:甲几何体的表面积为:14+14=28;
乙几何体的表面积为:14+1+5+8=28.
考点:几何体的表面积,简单组合体的三视图,作图﹣三视图
分析:(1)分别利用几何的形状得出组成的个数;(2)甲的左视图从左往右3列正方形的个数依次为2,2,2;乙的左视图从左往右3列正方形的个数依次为2,1,2;(3)直接利用几何体的形状进而得出表面积.
26. (1)解:
点D的坐标为(2,0)
(2)解:半径=OA2+OD2=42+22=20=25
∵OD=CE=2,OA=DE=4,∠AOD=∠CEO=90? ,
∴△AOD≌△CDE,
∴∠OAD=∠CDE,
∴∠ADO+∠CDE=∠ADO+∠OAD=90? ,
∴∠ADC=90?.
∴扇形DAC的圆心角度数为90?;
(3)解:设圆锥的底面半径是r,
则2πr=90π×25180
∴r=52
即该圆锥的底面半径为52.
考点:确定圆的条件,圆锥的计算
分析:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,从而作出弦AB,BC的垂直平分线,交点即为圆心D;
(2)根据方格纸的特点由勾股定理即可算出该圆的半径,连接DA,DC,根据SAS得到两个三角形全等△AOD≌△DCE,根据全等三角形的对应角相等得出∠OAD=∠CDE,根据直角三角形的两锐角互余及等量代换平角的定义即可得出∠ADC=90°,即扇形的圆心角是90°;
(3)根据圆锥的底面周长等于弧长,列出方程,求解即可。
