2020-2021学年华东师大版八年级下册数学 第19章矩形、菱形与正方形达标检测卷(word版含答案)
文档属性
| 名称 | 2020-2021学年华东师大版八年级下册数学 第19章矩形、菱形与正方形达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 299.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 05:33:04 | ||
图片预览



文档简介
第19章达标检测卷
一、选择题(每题3分,共30分)
1.下列命题为真命题的是( )
A.四个角相等的四边形是矩形 B.对角线垂直的四边形是菱形
C.对角线相等的四边形是矩形 D.四边相等的四边形是正方形
2.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )
A.20 B.15 C.10 D.5
3.如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的( )
A. B. C. D.
4.如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2),若反比例函数y=(x>0)的图象经过点A,则此反比例函数的表达式为( )
A.y=(x>0) B.y=-(x>0) C.y=-(x>0) D.y=(x>0)
5.如图,在正方形ABCD的内部,作等边三角形BCE,则∠AEB的度数为( )
A.60° B.65° C.70° D.75°
6.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
7.如图,把一张矩形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( )
A.15°或30°
B.30°或45°
C.45°或60°
D.30°或60°
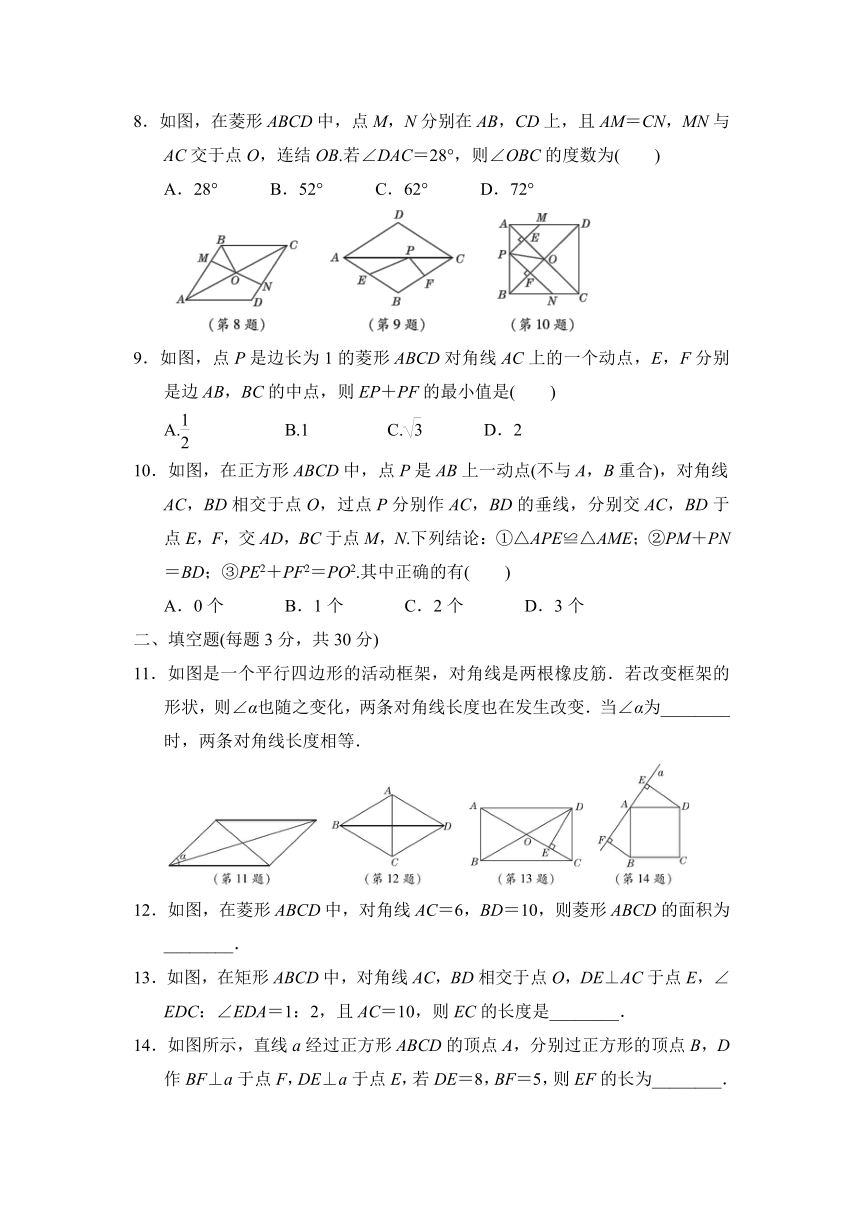
8.如图,在菱形ABCD中,点M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连结OB.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
9.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,E,F分别是边AB,BC的中点,则EP+PF的最小值是( )
A. B.1 C. D.2
10.如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每题3分,共30分)
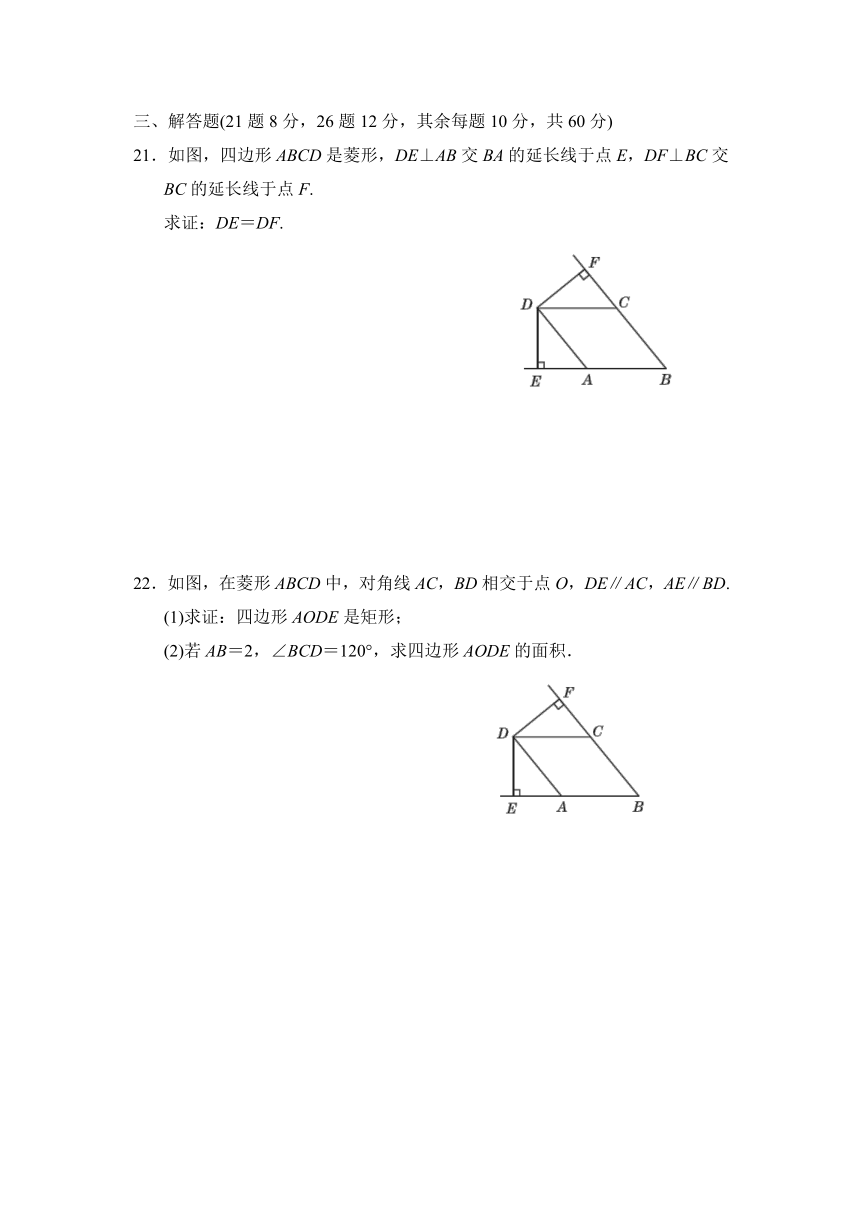
11.如图是一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为________时,两条对角线长度相等.
12.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.
13.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=10,则EC的长度是________.
14.如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B,D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为________.
15.菱形ABCD在直角坐标系中的位置如图所示,其中点A的
坐标为(1,0),点B的坐标为(0,),动点P从点A出发,
沿A→B→C→D→A→B→……的路径,在菱形的边上以
每秒1个单位长度的速度移动,移动到第2 022 s时,点
P的坐标为________.
16.如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连结DF,DF=4.设AB=x,AD=y,则x2+(y-4)2的值为________.
17.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ的周长的最小值为________.
18.如图,在矩形ABCD中,AB=4,BC=6,点E是AD上一点,把△ABE沿BE折叠,使点A落在点F处,点Q是CD上一点,将△BCQ沿BQ折叠,点C恰好落在直线BF上的点P处.若∠BQE=45°,则AE=________.
19.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF的中点,则AM的最小值为____________.
20.在平面直角坐标系中,正方形A1B1C1O、正方形A2B2C2C1、正方形A3B3C3C2、正方形A4B4C4C3、…、正方形AnBnCnCn-1按如图所示的方式放置,其中点A1,A2,A3,A4,…,An均在一次函数y=kx+b的图象上,点C1,C2,C3,C4,…,Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为________.
三、解答题(21题8分,26题12分,其余每题10分,共60分)
21.如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于点E,DF⊥BC交BC的延长线于点F.
求证:DE=DF.
22.如图,在菱形ABCD中,对角线AC,BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
23.如图,正方形ABCD的边长为4,E,F分别为DC,BC的中点.
(1)求证:△ADE≌△ABF;
(2)求△AEF的面积.
24.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连结AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
25.如图,在菱形ABCD中,E,F分别是BC,CD的中点.
(1)求证:△ABE≌△ADF;
(2)过点C作CG∥EA交AF于点H,交AD于点G,若∠BAE=30°,∠BCD=130°,求∠AHC的度数.
26.如图,在正方形ABCD的外侧作直线AP,点B关于直线AP的对称点为E,连结BE,DE,其中DE交直线AP于点F.
(1)依题意补全图①;
(2)若∠PAB=20°,求∠ADF的度数;
(3)如图②,若45°<∠PAB<90°,用等式表示线段AB,EF,FD之间的数量关系,并给出证明.
答案
一、1.A 2.B 3.B
4.D 点拨:∵菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2),
∴点A的坐标为(3,2),∴=2,
解得k=6,∴y=(x>0).故选D.
5.D
6.A 点拨:∵点C′是AB边的中点,AB=6,∴BC′=3,由图形折叠特性知,C′F=CF=BC-BF=9-BF.在Rt△C′BF中,BF2+BC′2=C′F2,
∴BF2+9=(9-BF)2,解得BF=4,故选A.
7.D 点拨:画出所剪的图形示意图如图所示.∵四边形ABCD是菱形,
∴∠ABD=∠ABC,∠BAC=∠BAD,AD∥BC.
∵∠BAD=120°,∴∠ABC=180°-∠BAD=180°-120°=60°.
∴∠ABD=30°,∠BAC=60°.
∴剪口与第二次折痕所成的角的度数应为30°或60°.故选D.
8.C
9.B
10.D 点拨:∵四边形ABCD是正方形,∴∠PAE=∠MAE=45°.
∵PM⊥AC,∴∠PEA=∠MEA=90°.
又∵AE=AE,∴△APE≌△AME,故①正确;由①得PE=ME,
∴PM=2PE.同理得PN=2PF,又易知PF=BF,四边形PEOF是矩形,
∴PN=2BF,PM=2FO,∴PM+PN=2FO+2BF=2BO=BD,故②正确;在Rt△PFO中,∵FO2+PF2=PO2,而PE=FO,∴PE2+PF2=PO2,故③正确.
二、11.90° 点拨:对角线相等的平行四边形是矩形.
12.30
13.2.5
14.13 点拨:∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠BAD=90°.
又∵∠FAB+∠FBA=∠FAB+∠EAD,
∴∠FBA=∠EAD.
∵BF⊥a于点F,DE⊥a于点E,
∴∠AFB=90°,∠DEA=90°.
在△AFB和△DEA中,
∵∠AFB=∠DEA,∠FBA=∠EAD,AB=DA,
∴△AFB≌△DEA(A.A.S.).
∴AF=DE=8,BF=AE=5.
∴EF=AF+AE=DE+BF=8+5=13.
15.
16.16 点拨:∵四边形ABCD是矩形,AB=x,AD=y,∴CD=AB=x,BC=AD=y,∠BCD=90°.又∵BD⊥DE,点F是BE的中点,DF=4,以BD,DE为邻边构造矩形,由矩形对角线的性质可知,BF=DF=EF=4,∴CF=4-BC=4-y.在Rt△DCF中,DC2+CF2=DF2,即x2+(4-y)2=42=16.∴x2+(y-4)2=16.
17.6 点拨:连结DE交AC于点Q′.∵四边形ABCD是正方形,∴点B与点D关于直线AC对称,∴DE的长即为BQ+QE的最小值,Q′是使△BEQ的周长为最小值时的点.由勾股定理得DE===5,∴△BEQ的周长的最小值=DE+BE=5+1=6.
18.2 点拨:由折叠知∠EBQ=∠ABC=45°.∵∠BQE=45°,∴∠BEQ=90°,BE=EQ.易证△BAE≌△EDQ,∴ED=AB=4,∴AE=AD-ED=6-4=2.
19.2.4 点拨:连结AP,在△ABC中,∵AB=6,AC=8,BC=10,∴AB2+AC2=BC2,∴∠BAC=90°.又∵PE⊥AB,PF⊥AC,∴四边形AFPE是矩形,∴EF=AP.∵M是EF的中点,∴AM=AP.根据直线外一点与直线上任意一点所连的线段中,垂线段最短,可知当AP⊥BC时,AP最短,同样AM也最短.当AP⊥BC时,AB·AC=BC·AP,即×6×8=×10×AP,
∴AP=4.8.∴AM的最小值为×4.8=2.4.
20.(2n-1-1,2n-1) 点拨:本题运用从特殊到一般的思想,由题意,得点A1(0,1),A2(1,2),A3(3,4),A4(7,8),…,根据以上总结规律,可得An(2n-1-1,2n-1).
三、21.证明:连结DB.∵四边形ABCD是菱形,∴BD平分∠ABC.
又∵DE⊥AB,DF⊥BC,∴DE=DF.
22.(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形.
在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形.
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°-120°=60°.
∵AB=BC=2,
∴△ABC是等边三角形,
∴OA=×2=1.
在菱形ABCD中,AC⊥BD,
∴∠AOB=90°,
∴由勾股定理得OB=.
∵四边形ABCD是菱形,
∴OD=OB=,
∴四边形AODE的面积=OA·OD=.
23.(1)证明:∵四边形ABCD为正方形,∴AB=AD=DC=CB,∠D=∠B=90°.∵E,F分别为DC,BC的中点,
∴DE=DC,BF=BC.
∴DE=BF.
在△ADE和△ABF中,
∴△ADE≌△ABF(S.A.S.).
(2)解:由题意知△ABF,△ADE,△CEF均为直角三角形,且AB=AD=4,DE=BF=CE=CF=×4=2,
∴S△AEF=S正方形ABCD-S△ADE-S△ABF-S△CEF=
4×4-×4×2-×4×2-×2×2=6.
24.(1)证明:∵四边形ABCD是正方形,∴∠B=∠D=90°,AD=AB.
由折叠可知,AD=AF,∠AFE=∠D=90°,
∴∠AFG=90°,AB=AF.
∴∠B=∠AFG=90°.
又∵AG=AG,
∴Rt△ABG≌Rt△AFG(H.L.).
(2)解:∵△ABG≌△AFG,
∴BG=FG.
设BG=FG=x,则GC=6-x,
∵E为CD的中点,
∴EF=DE=CE=3,
∴EG=x+3,
在Rt△CEG中,由勾股定理,
得32+(6-x)2=(x+3)2,
解得x=2,
∴BG=2.
25.(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D.
又∵E,F分别是BC,CD的中点,
∴BE=DF.在△ABE和△ADF中,
∵AB=AD,∠B=∠D,BE=DF,
∴△ABE≌△ADF(S.A.S.).
(2)解:∵四边形ABCD是菱形,
∠BCD=130°,
∴∠BAD=∠BCD=130°.
由(1)得△ABE≌△ADF,
∴∠DAF=∠BAE=30°.
∴∠EAH=∠BAD-∠BAE-∠DAF=130°-30°-30°=70°.
∵AE∥CG,
∴∠EAH+∠AHC=180°.
∴∠AHC=180°-∠EAH=180°-70°=110°.
26.解:(1)如图①.
(2)如图②,连结AE,
∵点E是点B关于直线AP的对称点,
∴∠PAE=∠PAB=20°,AE=AB.
∵四边形ABCD是正方形,
∴AE=AB=AD,∠BAD=90°.
∴∠AED=∠ADE,∠EAD=∠DAB+∠BAP+∠PAE=130°.
∴∠ADF==25°.
(3)EF2+FD2=2AB2.
证明如下:如图③,连结AE,BF,BD,由轴对称和正方形的性质可得,
EF=BF,AE=AB=AD,易得∠ABF=∠AEF=∠ADF,
∵∠BAD=90°,
∴∠ABF+∠FBD+∠ADB=90°.
∴∠ADF+∠ADB+∠FBD=90°.
∴∠BFD=90°.
在Rt△BFD中,由勾股定理得BF2+FD2=BD2.
在Rt△ABD中,由勾股定理得BD2=AB2+AD2=2AB2,
∴EF2+FD2=2AB2.
一、选择题(每题3分,共30分)
1.下列命题为真命题的是( )
A.四个角相等的四边形是矩形 B.对角线垂直的四边形是菱形
C.对角线相等的四边形是矩形 D.四边相等的四边形是正方形
2.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )
A.20 B.15 C.10 D.5
3.如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的( )
A. B. C. D.
4.如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2),若反比例函数y=(x>0)的图象经过点A,则此反比例函数的表达式为( )
A.y=(x>0) B.y=-(x>0) C.y=-(x>0) D.y=(x>0)
5.如图,在正方形ABCD的内部,作等边三角形BCE,则∠AEB的度数为( )
A.60° B.65° C.70° D.75°
6.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
7.如图,把一张矩形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( )
A.15°或30°
B.30°或45°
C.45°或60°
D.30°或60°
8.如图,在菱形ABCD中,点M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连结OB.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
9.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,E,F分别是边AB,BC的中点,则EP+PF的最小值是( )
A. B.1 C. D.2
10.如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每题3分,共30分)
11.如图是一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为________时,两条对角线长度相等.
12.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.
13.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=10,则EC的长度是________.
14.如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B,D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为________.
15.菱形ABCD在直角坐标系中的位置如图所示,其中点A的
坐标为(1,0),点B的坐标为(0,),动点P从点A出发,
沿A→B→C→D→A→B→……的路径,在菱形的边上以
每秒1个单位长度的速度移动,移动到第2 022 s时,点
P的坐标为________.
16.如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连结DF,DF=4.设AB=x,AD=y,则x2+(y-4)2的值为________.
17.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ的周长的最小值为________.
18.如图,在矩形ABCD中,AB=4,BC=6,点E是AD上一点,把△ABE沿BE折叠,使点A落在点F处,点Q是CD上一点,将△BCQ沿BQ折叠,点C恰好落在直线BF上的点P处.若∠BQE=45°,则AE=________.
19.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF的中点,则AM的最小值为____________.
20.在平面直角坐标系中,正方形A1B1C1O、正方形A2B2C2C1、正方形A3B3C3C2、正方形A4B4C4C3、…、正方形AnBnCnCn-1按如图所示的方式放置,其中点A1,A2,A3,A4,…,An均在一次函数y=kx+b的图象上,点C1,C2,C3,C4,…,Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为________.
三、解答题(21题8分,26题12分,其余每题10分,共60分)
21.如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于点E,DF⊥BC交BC的延长线于点F.
求证:DE=DF.
22.如图,在菱形ABCD中,对角线AC,BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
23.如图,正方形ABCD的边长为4,E,F分别为DC,BC的中点.
(1)求证:△ADE≌△ABF;
(2)求△AEF的面积.
24.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连结AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
25.如图,在菱形ABCD中,E,F分别是BC,CD的中点.
(1)求证:△ABE≌△ADF;
(2)过点C作CG∥EA交AF于点H,交AD于点G,若∠BAE=30°,∠BCD=130°,求∠AHC的度数.
26.如图,在正方形ABCD的外侧作直线AP,点B关于直线AP的对称点为E,连结BE,DE,其中DE交直线AP于点F.
(1)依题意补全图①;
(2)若∠PAB=20°,求∠ADF的度数;
(3)如图②,若45°<∠PAB<90°,用等式表示线段AB,EF,FD之间的数量关系,并给出证明.
答案
一、1.A 2.B 3.B
4.D 点拨:∵菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2),
∴点A的坐标为(3,2),∴=2,
解得k=6,∴y=(x>0).故选D.
5.D
6.A 点拨:∵点C′是AB边的中点,AB=6,∴BC′=3,由图形折叠特性知,C′F=CF=BC-BF=9-BF.在Rt△C′BF中,BF2+BC′2=C′F2,
∴BF2+9=(9-BF)2,解得BF=4,故选A.
7.D 点拨:画出所剪的图形示意图如图所示.∵四边形ABCD是菱形,
∴∠ABD=∠ABC,∠BAC=∠BAD,AD∥BC.
∵∠BAD=120°,∴∠ABC=180°-∠BAD=180°-120°=60°.
∴∠ABD=30°,∠BAC=60°.
∴剪口与第二次折痕所成的角的度数应为30°或60°.故选D.
8.C
9.B
10.D 点拨:∵四边形ABCD是正方形,∴∠PAE=∠MAE=45°.
∵PM⊥AC,∴∠PEA=∠MEA=90°.
又∵AE=AE,∴△APE≌△AME,故①正确;由①得PE=ME,
∴PM=2PE.同理得PN=2PF,又易知PF=BF,四边形PEOF是矩形,
∴PN=2BF,PM=2FO,∴PM+PN=2FO+2BF=2BO=BD,故②正确;在Rt△PFO中,∵FO2+PF2=PO2,而PE=FO,∴PE2+PF2=PO2,故③正确.
二、11.90° 点拨:对角线相等的平行四边形是矩形.
12.30
13.2.5
14.13 点拨:∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠BAD=90°.
又∵∠FAB+∠FBA=∠FAB+∠EAD,
∴∠FBA=∠EAD.
∵BF⊥a于点F,DE⊥a于点E,
∴∠AFB=90°,∠DEA=90°.
在△AFB和△DEA中,
∵∠AFB=∠DEA,∠FBA=∠EAD,AB=DA,
∴△AFB≌△DEA(A.A.S.).
∴AF=DE=8,BF=AE=5.
∴EF=AF+AE=DE+BF=8+5=13.
15.
16.16 点拨:∵四边形ABCD是矩形,AB=x,AD=y,∴CD=AB=x,BC=AD=y,∠BCD=90°.又∵BD⊥DE,点F是BE的中点,DF=4,以BD,DE为邻边构造矩形,由矩形对角线的性质可知,BF=DF=EF=4,∴CF=4-BC=4-y.在Rt△DCF中,DC2+CF2=DF2,即x2+(4-y)2=42=16.∴x2+(y-4)2=16.
17.6 点拨:连结DE交AC于点Q′.∵四边形ABCD是正方形,∴点B与点D关于直线AC对称,∴DE的长即为BQ+QE的最小值,Q′是使△BEQ的周长为最小值时的点.由勾股定理得DE===5,∴△BEQ的周长的最小值=DE+BE=5+1=6.
18.2 点拨:由折叠知∠EBQ=∠ABC=45°.∵∠BQE=45°,∴∠BEQ=90°,BE=EQ.易证△BAE≌△EDQ,∴ED=AB=4,∴AE=AD-ED=6-4=2.
19.2.4 点拨:连结AP,在△ABC中,∵AB=6,AC=8,BC=10,∴AB2+AC2=BC2,∴∠BAC=90°.又∵PE⊥AB,PF⊥AC,∴四边形AFPE是矩形,∴EF=AP.∵M是EF的中点,∴AM=AP.根据直线外一点与直线上任意一点所连的线段中,垂线段最短,可知当AP⊥BC时,AP最短,同样AM也最短.当AP⊥BC时,AB·AC=BC·AP,即×6×8=×10×AP,
∴AP=4.8.∴AM的最小值为×4.8=2.4.
20.(2n-1-1,2n-1) 点拨:本题运用从特殊到一般的思想,由题意,得点A1(0,1),A2(1,2),A3(3,4),A4(7,8),…,根据以上总结规律,可得An(2n-1-1,2n-1).
三、21.证明:连结DB.∵四边形ABCD是菱形,∴BD平分∠ABC.
又∵DE⊥AB,DF⊥BC,∴DE=DF.
22.(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形.
在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形.
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°-120°=60°.
∵AB=BC=2,
∴△ABC是等边三角形,
∴OA=×2=1.
在菱形ABCD中,AC⊥BD,
∴∠AOB=90°,
∴由勾股定理得OB=.
∵四边形ABCD是菱形,
∴OD=OB=,
∴四边形AODE的面积=OA·OD=.
23.(1)证明:∵四边形ABCD为正方形,∴AB=AD=DC=CB,∠D=∠B=90°.∵E,F分别为DC,BC的中点,
∴DE=DC,BF=BC.
∴DE=BF.
在△ADE和△ABF中,
∴△ADE≌△ABF(S.A.S.).
(2)解:由题意知△ABF,△ADE,△CEF均为直角三角形,且AB=AD=4,DE=BF=CE=CF=×4=2,
∴S△AEF=S正方形ABCD-S△ADE-S△ABF-S△CEF=
4×4-×4×2-×4×2-×2×2=6.
24.(1)证明:∵四边形ABCD是正方形,∴∠B=∠D=90°,AD=AB.
由折叠可知,AD=AF,∠AFE=∠D=90°,
∴∠AFG=90°,AB=AF.
∴∠B=∠AFG=90°.
又∵AG=AG,
∴Rt△ABG≌Rt△AFG(H.L.).
(2)解:∵△ABG≌△AFG,
∴BG=FG.
设BG=FG=x,则GC=6-x,
∵E为CD的中点,
∴EF=DE=CE=3,
∴EG=x+3,
在Rt△CEG中,由勾股定理,
得32+(6-x)2=(x+3)2,
解得x=2,
∴BG=2.
25.(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D.
又∵E,F分别是BC,CD的中点,
∴BE=DF.在△ABE和△ADF中,
∵AB=AD,∠B=∠D,BE=DF,
∴△ABE≌△ADF(S.A.S.).
(2)解:∵四边形ABCD是菱形,
∠BCD=130°,
∴∠BAD=∠BCD=130°.
由(1)得△ABE≌△ADF,
∴∠DAF=∠BAE=30°.
∴∠EAH=∠BAD-∠BAE-∠DAF=130°-30°-30°=70°.
∵AE∥CG,
∴∠EAH+∠AHC=180°.
∴∠AHC=180°-∠EAH=180°-70°=110°.
26.解:(1)如图①.
(2)如图②,连结AE,
∵点E是点B关于直线AP的对称点,
∴∠PAE=∠PAB=20°,AE=AB.
∵四边形ABCD是正方形,
∴AE=AB=AD,∠BAD=90°.
∴∠AED=∠ADE,∠EAD=∠DAB+∠BAP+∠PAE=130°.
∴∠ADF==25°.
(3)EF2+FD2=2AB2.
证明如下:如图③,连结AE,BF,BD,由轴对称和正方形的性质可得,
EF=BF,AE=AB=AD,易得∠ABF=∠AEF=∠ADF,
∵∠BAD=90°,
∴∠ABF+∠FBD+∠ADB=90°.
∴∠ADF+∠ADB+∠FBD=90°.
∴∠BFD=90°.
在Rt△BFD中,由勾股定理得BF2+FD2=BD2.
在Rt△ABD中,由勾股定理得BD2=AB2+AD2=2AB2,
∴EF2+FD2=2AB2.
