6.2 向心力 同步练习—2020-2021学年【新教材】人教版(2019)高中物理必修第二册
文档属性
| 名称 | 6.2 向心力 同步练习—2020-2021学年【新教材】人教版(2019)高中物理必修第二册 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-24 00:00:00 | ||
图片预览




文档简介
第六章 第二节 向心力 同步练习
【基 础 训 练】
1.关于向心力的说法正确的是( )
A.物体由于做圆周运动而产生了向心力
B.向心力不改变圆周运动中物体线速度的大小
C.对做匀速圆周运动的物体进行受力分析时,一定不要漏掉向心力
D.做匀速圆周运动的物体其向心力是不变的
2.场地自行车比赛中,运动员在弯道处转弯的情境如图1所示,弯道处的路面是倾斜的,假设运动员转弯时在水平圆轨道上做匀速圆周运动,此过程的自行车(含运动员)除受空气阻力和摩擦力外,还受到( )
图1
A.重力和支持力 B.支持力和向心力
C.重力和向心力 D.重力、支持力和向心力
3.如图2所示,在光滑水平面上,一质量为m的小球在绳的拉力作用下做半径为r的匀速圆周运动,小球运动线速度的大小为v,则绳的拉力F大小为( )
图2
A.m B.m
C.mvr D.mvr2
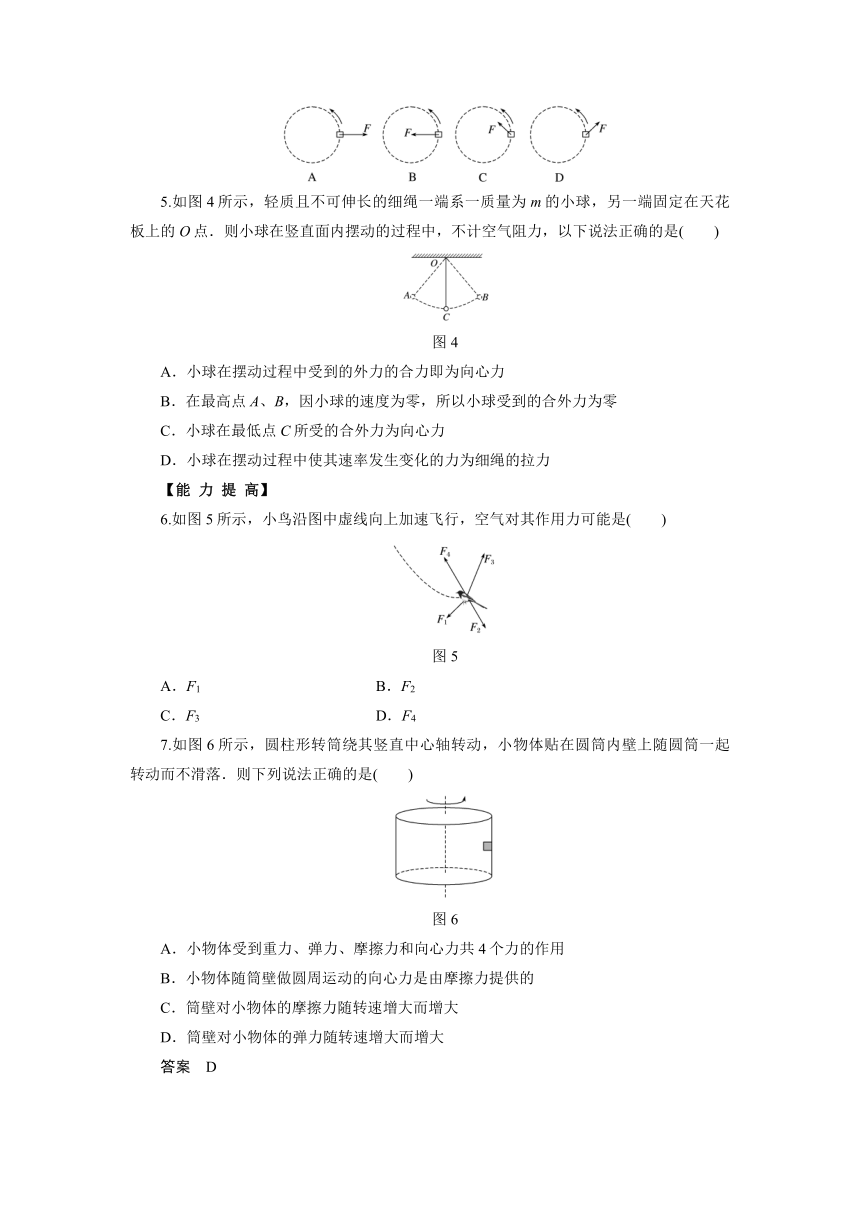
4.如图3,一水平圆盘可绕一通过圆心且垂直于盘面的竖直轴转动,在圆盘上放一块橡皮,橡皮块随圆盘一起转动(俯视为逆时针).某段时间内圆盘转速不断增大,但橡皮块仍相对圆盘静止,在这段时间内,关于橡皮块所受合力F的方向的四种表示(俯视图)中,正确的是( )
图3
5.如图4所示,轻质且不可伸长的细绳一端系一质量为m的小球,另一端固定在天花板上的O点.则小球在竖直面内摆动的过程中,不计空气阻力,以下说法正确的是( )
图4
A.小球在摆动过程中受到的外力的合力即为向心力
B.在最高点A、B,因小球的速度为零,所以小球受到的合外力为零
C.小球在最低点C所受的合外力为向心力
D.小球在摆动过程中使其速率发生变化的力为细绳的拉力
【能 力 提 高】
6.如图5所示,小鸟沿图中虚线向上加速飞行,空气对其作用力可能是( )
图5
A.F1 B.F2
C.F3 D.F4
7.如图6所示,圆柱形转筒绕其竖直中心轴转动,小物体贴在圆筒内壁上随圆筒一起转动而不滑落.则下列说法正确的是( )
图6
A.小物体受到重力、弹力、摩擦力和向心力共4个力的作用
B.小物体随筒壁做圆周运动的向心力是由摩擦力提供的
C.筒壁对小物体的摩擦力随转速增大而增大
D.筒壁对小物体的弹力随转速增大而增大
答案 D
8.(多选)质量为m的小球用长为L的轻质细线悬挂在O点,在O点的正下方处有一光滑小钉子P,把细线沿水平方向拉直,如图7所示,无初速度地释放小球,当细线碰到钉子的瞬间(瞬时速度不变),设细线没有断裂,则下列说法正确的是( )
图7
A.小球的角速度突然增大
B.小球的角速度突然减小
C.小球对细线的拉力突然增大
D.小球对细线的拉力保持不变
9.一质量为m的物体,沿半径为R的半圆形轨道滑行,如图8所示,经过最低点时的速度为v,物体与轨道间的动摩擦因数为μ,重力加速度为g,则它在最低点时受到的摩擦力大小为( )
图8
A.μmg B.
C.μm(g+) D.μm(g-)
10.如图9所示,在水平转动的圆盘上,两个完全一样的木块A、B一起随圆盘做匀速圆周运动,转动的角速度为ω,已知木块A、B到圆盘中心O的距离分别为rA和rB,则两木块的向心力之比为( )
图9
A.rA∶rB B.rB∶rA
C.rA2∶rB2 D.rB2∶rA2
11.甲、乙两人在光滑的冰面上,面对面拉着弹簧测力计做圆周运动,如图10所示。m甲=80 kg,m乙=40 kg,两人相距0.9 m,弹簧测力计的示数为9.2 N,则下列判断正确的是( )
图10
A.两人的线速度相同,约为40 m/s
B.两人的角速度相同,约为6 rad/s
C.两人的运动半径相同,都是0.45 m
D.两人的运动半径不同,甲为0.3 m,乙为0.6 m
12.如图11所示,把一个长为20 cm、劲度系数为360 N/m的弹簧一端固定,作为圆心,弹簧的另一端连接一个质量为0.50 kg的小球。当小球以 r/min 的转速在光滑水平面上做匀速圆周运动时,弹簧的伸长量应为( )
图11
A.5.2 cm B.5.3 cm
C.5.0 cm D.5.4 cm
13.如图12所示,可视为质点的木块A、B叠放在一起,放在水平转台上随转台一起绕固定转轴OO′匀速转动,木块A、B与转轴OO′的距离为1 m,A的质量为5 kg,B的质量为10 kg。已知A与B间的动摩擦因数为0.2,B与转台间的动摩擦因数为0.3,若木块A、B与转台始终保持相对静止,则转台角速度ω的最大值为(最大静摩擦力等于滑动摩擦力,g取10 m/s2)( )
图12
A.1 rad/s B. rad/s
C. rad/s D.3 rad/s
14.(多选)如图13所示,在双人花样滑冰运动中,有时会看到被男运动员拉着的女运动员离开地面在空中做圆锥摆运动的精彩场面,目测质量为m的女运动员做圆锥摆运动时和水平冰面的夹角约为30°,运动员转动的周期T=2 s,重力加速度为g,估算可知该女运动员( )
图13
A.受到的拉力为mg
B.受到的拉力为2mg
C.做圆周运动的半径为
D.做圆周运动的半径为
15.(多选)如图14所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则下列说法正确的是( )
图14
A.球A的线速度必定大于球B的线速度
B.球A的角速度必定小于球B的角速度
C.球A的运动周期必定小于球B的运动周期
D.球A对筒壁的压力必定大于球B对筒壁的压力
16.如图15所示,水平转盘的中心有一个光滑的竖直小圆孔,质量为m的物体A放在转盘上,物体A到圆孔的距离为r,物体A通过轻绳与物体B相连,物体B的质量也为m。若物体A与转盘间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,则转盘转动的角速度ω在什么范围内,才能使物体A随转盘转动而不滑动?
图15
第六章 第二节 向心力 同步练习
【基 础 训 练】
1.关于向心力的说法正确的是( )
A.物体由于做圆周运动而产生了向心力
B.向心力不改变圆周运动中物体线速度的大小
C.对做匀速圆周运动的物体进行受力分析时,一定不要漏掉向心力
D.做匀速圆周运动的物体其向心力是不变的
答案 B
解析 向心力是物体做圆周运动的原因,故A错误;因向心力始终垂直于线速度方向,所以它不改变线速度的大小,只改变线速度的方向,当合外力完全提供向心力时,物体就做匀速圆周运动,该合力大小不变,方向时刻改变,即向心力是变力,故B正确,D错误;向心力是根据力的作用效果命名的,它可能是某种性质的力,也可能是某个力的分力或几个力的合力,受力分析时不能加入向心力,故C错误.
2.场地自行车比赛中,运动员在弯道处转弯的情境如图1所示,弯道处的路面是倾斜的,假设运动员转弯时在水平圆轨道上做匀速圆周运动,此过程的自行车(含运动员)除受空气阻力和摩擦力外,还受到( )
图1
A.重力和支持力 B.支持力和向心力
C.重力和向心力 D.重力、支持力和向心力
解析:选A 自行车转弯时所需的向心力由重力、路面的支持力、空气阻力与摩擦力的合力提供,向心力是效果力,不是物体实际受到的力,所以只有选项A正确。
3.如图2所示,在光滑水平面上,一质量为m的小球在绳的拉力作用下做半径为r的匀速圆周运动,小球运动线速度的大小为v,则绳的拉力F大小为( )
图2
A.m B.m
C.mvr D.mvr2
解析:选B 根据绳的拉力提供小球做匀速圆周运动的向心力,有Fn=m,故B正确。
4.如图3,一水平圆盘可绕一通过圆心且垂直于盘面的竖直轴转动,在圆盘上放一块橡皮,橡皮块随圆盘一起转动(俯视为逆时针).某段时间内圆盘转速不断增大,但橡皮块仍相对圆盘静止,在这段时间内,关于橡皮块所受合力F的方向的四种表示(俯视图)中,正确的是( )
图3
答案 C
解析 橡皮块做加速圆周运动,合力不指向圆心,但一定指向圆周的内侧;由于做加速圆周运动,速度不断增大,故合力与速度的夹角小于90°,故选C.
5.如图4所示,轻质且不可伸长的细绳一端系一质量为m的小球,另一端固定在天花板上的O点.则小球在竖直面内摆动的过程中,不计空气阻力,以下说法正确的是( )
图4
A.小球在摆动过程中受到的外力的合力即为向心力
B.在最高点A、B,因小球的速度为零,所以小球受到的合外力为零
C.小球在最低点C所受的合外力为向心力
D.小球在摆动过程中使其速率发生变化的力为细绳的拉力
答案 C
解析 小球在摆动过程中受到的合外力只有在小球运动到C点时全部充当向心力,故A错误,C正确;小球运动到最高点时,虽然小球的速度为零,但小球受到的合外力不为零,故B错误;小球在摆动过程中使其速率发生变化的力为重力垂直于细绳方向的分力,故D错误.
【能 力 提 高】
6.如图5所示,小鸟沿图中虚线向上加速飞行,空气对其作用力可能是( )
图5
A.F1 B.F2
C.F3 D.F4
答案 D
7.如图6所示,圆柱形转筒绕其竖直中心轴转动,小物体贴在圆筒内壁上随圆筒一起转动而不滑落.则下列说法正确的是( )
图6
A.小物体受到重力、弹力、摩擦力和向心力共4个力的作用
B.小物体随筒壁做圆周运动的向心力是由摩擦力提供的
C.筒壁对小物体的摩擦力随转速增大而增大
D.筒壁对小物体的弹力随转速增大而增大
答案 D
解析 小物体随转筒一起做圆周运动,受重力、弹力和静摩擦力共3个力的作用,故选项A错误.水平方向上,弹力指向圆心,提供向心力,据牛顿第二定律有:FN=mω2r,又ω=2πn,可知转速越大,角速度越大,小物体所受的弹力就越大,故选项B错误,D正确;在竖直方向上,小物体所受的重力和静摩擦力平衡,静摩擦力大小不变,故选项C错误.
8.(多选)质量为m的小球用长为L的轻质细线悬挂在O点,在O点的正下方处有一光滑小钉子P,把细线沿水平方向拉直,如图7所示,无初速度地释放小球,当细线碰到钉子的瞬间(瞬时速度不变),设细线没有断裂,则下列说法正确的是( )
图7
A.小球的角速度突然增大
B.小球的角速度突然减小
C.小球对细线的拉力突然增大
D.小球对细线的拉力保持不变
答案 AC
解析 根据题意,细线碰到钉子的瞬间,小球的瞬时速度v不变,但其做圆周运动的半径从L突变为,由ω=可知小球的角速度突然增大,选项A正确,B错误;根据FT-mg=m可知小球受到的拉力增大,由牛顿第三定律知,小球对细线的拉力增大,选项C正确,D错误.
9.一质量为m的物体,沿半径为R的半圆形轨道滑行,如图8所示,经过最低点时的速度为v,物体与轨道间的动摩擦因数为μ,重力加速度为g,则它在最低点时受到的摩擦力大小为( )
图8
A.μmg B.
C.μm(g+) D.μm(g-)
答案 C
解析 在最低点由向心力公式得:FN-mg=m,得FN=mg+m,又由摩擦力公式有Ff=μFN=μ(mg+m)=μm(g+),C选项正确.
10.如图9所示,在水平转动的圆盘上,两个完全一样的木块A、B一起随圆盘做匀速圆周运动,转动的角速度为ω,已知木块A、B到圆盘中心O的距离分别为rA和rB,则两木块的向心力之比为( )
图9
A.rA∶rB B.rB∶rA
C.rA2∶rB2 D.rB2∶rA2
解析:选A 木块A、B在绕O点转动的过程中,是木块与圆盘间的静摩擦力提供了木块做匀速圆周运动所需的向心力,因两木块旋转的角速度ω等大,质量一样,由向心力公式Fn=mrω2,得FA=mrAω2,FB=mrBω2,解得FA∶FB=rA∶rB,故A正确。
11.甲、乙两人在光滑的冰面上,面对面拉着弹簧测力计做圆周运动,如图10所示。m甲=80 kg,m乙=40 kg,两人相距0.9 m,弹簧测力计的示数为9.2 N,则下列判断正确的是( )
图10
A.两人的线速度相同,约为40 m/s
B.两人的角速度相同,约为6 rad/s
C.两人的运动半径相同,都是0.45 m
D.两人的运动半径不同,甲为0.3 m,乙为0.6 m
解析:选D 两人做圆周运动的角速度相同,向心力相同,设两人的运动半径分别为r甲和r乙,由向心力公式和圆周运动规律,得m甲r甲ω2=m乙r乙ω2,所以==,又因为r甲+r乙=0.9 m,所以r甲=0.3 m,r乙=0.6 m,C错误,D正确。由v=ωr得两人运动的线速度之比==,A错误。由Fn=m甲r甲ω2,得ω== rad/s≈0.6 rad/s,B错误。
12.如图11所示,把一个长为20 cm、劲度系数为360 N/m的弹簧一端固定,作为圆心,弹簧的另一端连接一个质量为0.50 kg的小球。当小球以 r/min 的转速在光滑水平面上做匀速圆周运动时,弹簧的伸长量应为( )
图11
A.5.2 cm B.5.3 cm
C.5.0 cm D.5.4 cm
解析:选C 小球转动的角速度ω=2nπ=rad/s=12 rad/s,由向心力公式,得kx=mω2(x0+x),解得x== m=0.05 m=5.0 cm,选项C正确。
13.如图12所示,可视为质点的木块A、B叠放在一起,放在水平转台上随转台一起绕固定转轴OO′匀速转动,木块A、B与转轴OO′的距离为1 m,A的质量为5 kg,B的质量为10 kg。已知A与B间的动摩擦因数为0.2,B与转台间的动摩擦因数为0.3,若木块A、B与转台始终保持相对静止,则转台角速度ω的最大值为(最大静摩擦力等于滑动摩擦力,g取10 m/s2)( )
图12
A.1 rad/s B. rad/s
C. rad/s D.3 rad/s
解析:选B 对A有μ1mAg≥mAω2r,对A、B整体有(mA+mB)ω2r≤μ2(mA+mB)g,代入数据解得ω≤ rad/s,故B正确。
14.(多选)如图13所示,在双人花样滑冰运动中,有时会看到被男运动员拉着的女运动员离开地面在空中做圆锥摆运动的精彩场面,目测质量为m的女运动员做圆锥摆运动时和水平冰面的夹角约为30°,运动员转动的周期T=2 s,重力加速度为g,估算可知该女运动员( )
图13
A.受到的拉力为mg
B.受到的拉力为2mg
C.做圆周运动的半径为
D.做圆周运动的半径为
解析:选BC 设女运动员受到的拉力为F,分析女运动员受力情况可知,Fsin 30°=mg,Fcos 30°=mr,解得F=2mg,r=,故B、C正确。
15.(多选)如图14所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则下列说法正确的是( )
图14
A.球A的线速度必定大于球B的线速度
B.球A的角速度必定小于球B的角速度
C.球A的运动周期必定小于球B的运动周期
D.球A对筒壁的压力必定大于球B对筒壁的压力
解析:选AB 两球均贴着圆锥筒的内壁在水平面内做匀速圆周运动,它们均受到重力和筒壁对它们的支持力FN的作用,其合力必定在水平面内时刻指向圆心,如图所示,可知,筒壁对球的支持力FN=,故A、B两球对筒壁的压力大小相等,选项D错误。
由球所受合力提供其做匀速圆周运动的向心力,得mgcot θ=m=mω2r=m,小球的线速度v=,角速度ω= ,周期T=2π 。由此可见,小球的线速度随轨道半径的增大而增大,所以A球的线速度必定大于B球的线速度,选项A正确。小球的角速度随半径的增大而减小,周期随半径的增大而增大,所以A球的角速度小于B球的角速度,A球的周期大于B球的周期,选项B正确,选项C错误。
16.如图15所示,水平转盘的中心有一个光滑的竖直小圆孔,质量为m的物体A放在转盘上,物体A到圆孔的距离为r,物体A通过轻绳与物体B相连,物体B的质量也为m。若物体A与转盘间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,则转盘转动的角速度ω在什么范围内,才能使物体A随转盘转动而不滑动?
图15
解析:当A将要沿转盘背离圆心滑动时,A所受的摩擦力为最大静摩擦力,方向指向圆心,此时A做圆周运动所需的向心力为绳的拉力与最大静摩擦力的合力,即
F+Ffmax=mrω12 ①
由于B静止,故有F=mg ②
又Ffmax=μFN=μmg ③
由①②③式可得ω1=
当A将要沿转盘向圆心滑动时,A所受的摩擦力为最大静摩擦力,方向背离圆心,此时A做圆周运动所需的向心力为
F-Ffmax=mrω22 ④
由②③④式可得ω2=
故要使A随转盘一起转动而不滑动,其角速度ω的范围为ω2≤ω≤ω1,即 ≤ω≤ 。
答案: ≤ω≤
【基 础 训 练】
1.关于向心力的说法正确的是( )
A.物体由于做圆周运动而产生了向心力
B.向心力不改变圆周运动中物体线速度的大小
C.对做匀速圆周运动的物体进行受力分析时,一定不要漏掉向心力
D.做匀速圆周运动的物体其向心力是不变的
2.场地自行车比赛中,运动员在弯道处转弯的情境如图1所示,弯道处的路面是倾斜的,假设运动员转弯时在水平圆轨道上做匀速圆周运动,此过程的自行车(含运动员)除受空气阻力和摩擦力外,还受到( )
图1
A.重力和支持力 B.支持力和向心力
C.重力和向心力 D.重力、支持力和向心力
3.如图2所示,在光滑水平面上,一质量为m的小球在绳的拉力作用下做半径为r的匀速圆周运动,小球运动线速度的大小为v,则绳的拉力F大小为( )
图2
A.m B.m
C.mvr D.mvr2
4.如图3,一水平圆盘可绕一通过圆心且垂直于盘面的竖直轴转动,在圆盘上放一块橡皮,橡皮块随圆盘一起转动(俯视为逆时针).某段时间内圆盘转速不断增大,但橡皮块仍相对圆盘静止,在这段时间内,关于橡皮块所受合力F的方向的四种表示(俯视图)中,正确的是( )
图3
5.如图4所示,轻质且不可伸长的细绳一端系一质量为m的小球,另一端固定在天花板上的O点.则小球在竖直面内摆动的过程中,不计空气阻力,以下说法正确的是( )
图4
A.小球在摆动过程中受到的外力的合力即为向心力
B.在最高点A、B,因小球的速度为零,所以小球受到的合外力为零
C.小球在最低点C所受的合外力为向心力
D.小球在摆动过程中使其速率发生变化的力为细绳的拉力
【能 力 提 高】
6.如图5所示,小鸟沿图中虚线向上加速飞行,空气对其作用力可能是( )
图5
A.F1 B.F2
C.F3 D.F4
7.如图6所示,圆柱形转筒绕其竖直中心轴转动,小物体贴在圆筒内壁上随圆筒一起转动而不滑落.则下列说法正确的是( )
图6
A.小物体受到重力、弹力、摩擦力和向心力共4个力的作用
B.小物体随筒壁做圆周运动的向心力是由摩擦力提供的
C.筒壁对小物体的摩擦力随转速增大而增大
D.筒壁对小物体的弹力随转速增大而增大
答案 D
8.(多选)质量为m的小球用长为L的轻质细线悬挂在O点,在O点的正下方处有一光滑小钉子P,把细线沿水平方向拉直,如图7所示,无初速度地释放小球,当细线碰到钉子的瞬间(瞬时速度不变),设细线没有断裂,则下列说法正确的是( )
图7
A.小球的角速度突然增大
B.小球的角速度突然减小
C.小球对细线的拉力突然增大
D.小球对细线的拉力保持不变
9.一质量为m的物体,沿半径为R的半圆形轨道滑行,如图8所示,经过最低点时的速度为v,物体与轨道间的动摩擦因数为μ,重力加速度为g,则它在最低点时受到的摩擦力大小为( )
图8
A.μmg B.
C.μm(g+) D.μm(g-)
10.如图9所示,在水平转动的圆盘上,两个完全一样的木块A、B一起随圆盘做匀速圆周运动,转动的角速度为ω,已知木块A、B到圆盘中心O的距离分别为rA和rB,则两木块的向心力之比为( )
图9
A.rA∶rB B.rB∶rA
C.rA2∶rB2 D.rB2∶rA2
11.甲、乙两人在光滑的冰面上,面对面拉着弹簧测力计做圆周运动,如图10所示。m甲=80 kg,m乙=40 kg,两人相距0.9 m,弹簧测力计的示数为9.2 N,则下列判断正确的是( )
图10
A.两人的线速度相同,约为40 m/s
B.两人的角速度相同,约为6 rad/s
C.两人的运动半径相同,都是0.45 m
D.两人的运动半径不同,甲为0.3 m,乙为0.6 m
12.如图11所示,把一个长为20 cm、劲度系数为360 N/m的弹簧一端固定,作为圆心,弹簧的另一端连接一个质量为0.50 kg的小球。当小球以 r/min 的转速在光滑水平面上做匀速圆周运动时,弹簧的伸长量应为( )
图11
A.5.2 cm B.5.3 cm
C.5.0 cm D.5.4 cm
13.如图12所示,可视为质点的木块A、B叠放在一起,放在水平转台上随转台一起绕固定转轴OO′匀速转动,木块A、B与转轴OO′的距离为1 m,A的质量为5 kg,B的质量为10 kg。已知A与B间的动摩擦因数为0.2,B与转台间的动摩擦因数为0.3,若木块A、B与转台始终保持相对静止,则转台角速度ω的最大值为(最大静摩擦力等于滑动摩擦力,g取10 m/s2)( )
图12
A.1 rad/s B. rad/s
C. rad/s D.3 rad/s
14.(多选)如图13所示,在双人花样滑冰运动中,有时会看到被男运动员拉着的女运动员离开地面在空中做圆锥摆运动的精彩场面,目测质量为m的女运动员做圆锥摆运动时和水平冰面的夹角约为30°,运动员转动的周期T=2 s,重力加速度为g,估算可知该女运动员( )
图13
A.受到的拉力为mg
B.受到的拉力为2mg
C.做圆周运动的半径为
D.做圆周运动的半径为
15.(多选)如图14所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则下列说法正确的是( )
图14
A.球A的线速度必定大于球B的线速度
B.球A的角速度必定小于球B的角速度
C.球A的运动周期必定小于球B的运动周期
D.球A对筒壁的压力必定大于球B对筒壁的压力
16.如图15所示,水平转盘的中心有一个光滑的竖直小圆孔,质量为m的物体A放在转盘上,物体A到圆孔的距离为r,物体A通过轻绳与物体B相连,物体B的质量也为m。若物体A与转盘间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,则转盘转动的角速度ω在什么范围内,才能使物体A随转盘转动而不滑动?
图15
第六章 第二节 向心力 同步练习
【基 础 训 练】
1.关于向心力的说法正确的是( )
A.物体由于做圆周运动而产生了向心力
B.向心力不改变圆周运动中物体线速度的大小
C.对做匀速圆周运动的物体进行受力分析时,一定不要漏掉向心力
D.做匀速圆周运动的物体其向心力是不变的
答案 B
解析 向心力是物体做圆周运动的原因,故A错误;因向心力始终垂直于线速度方向,所以它不改变线速度的大小,只改变线速度的方向,当合外力完全提供向心力时,物体就做匀速圆周运动,该合力大小不变,方向时刻改变,即向心力是变力,故B正确,D错误;向心力是根据力的作用效果命名的,它可能是某种性质的力,也可能是某个力的分力或几个力的合力,受力分析时不能加入向心力,故C错误.
2.场地自行车比赛中,运动员在弯道处转弯的情境如图1所示,弯道处的路面是倾斜的,假设运动员转弯时在水平圆轨道上做匀速圆周运动,此过程的自行车(含运动员)除受空气阻力和摩擦力外,还受到( )
图1
A.重力和支持力 B.支持力和向心力
C.重力和向心力 D.重力、支持力和向心力
解析:选A 自行车转弯时所需的向心力由重力、路面的支持力、空气阻力与摩擦力的合力提供,向心力是效果力,不是物体实际受到的力,所以只有选项A正确。
3.如图2所示,在光滑水平面上,一质量为m的小球在绳的拉力作用下做半径为r的匀速圆周运动,小球运动线速度的大小为v,则绳的拉力F大小为( )
图2
A.m B.m
C.mvr D.mvr2
解析:选B 根据绳的拉力提供小球做匀速圆周运动的向心力,有Fn=m,故B正确。
4.如图3,一水平圆盘可绕一通过圆心且垂直于盘面的竖直轴转动,在圆盘上放一块橡皮,橡皮块随圆盘一起转动(俯视为逆时针).某段时间内圆盘转速不断增大,但橡皮块仍相对圆盘静止,在这段时间内,关于橡皮块所受合力F的方向的四种表示(俯视图)中,正确的是( )
图3
答案 C
解析 橡皮块做加速圆周运动,合力不指向圆心,但一定指向圆周的内侧;由于做加速圆周运动,速度不断增大,故合力与速度的夹角小于90°,故选C.
5.如图4所示,轻质且不可伸长的细绳一端系一质量为m的小球,另一端固定在天花板上的O点.则小球在竖直面内摆动的过程中,不计空气阻力,以下说法正确的是( )
图4
A.小球在摆动过程中受到的外力的合力即为向心力
B.在最高点A、B,因小球的速度为零,所以小球受到的合外力为零
C.小球在最低点C所受的合外力为向心力
D.小球在摆动过程中使其速率发生变化的力为细绳的拉力
答案 C
解析 小球在摆动过程中受到的合外力只有在小球运动到C点时全部充当向心力,故A错误,C正确;小球运动到最高点时,虽然小球的速度为零,但小球受到的合外力不为零,故B错误;小球在摆动过程中使其速率发生变化的力为重力垂直于细绳方向的分力,故D错误.
【能 力 提 高】
6.如图5所示,小鸟沿图中虚线向上加速飞行,空气对其作用力可能是( )
图5
A.F1 B.F2
C.F3 D.F4
答案 D
7.如图6所示,圆柱形转筒绕其竖直中心轴转动,小物体贴在圆筒内壁上随圆筒一起转动而不滑落.则下列说法正确的是( )
图6
A.小物体受到重力、弹力、摩擦力和向心力共4个力的作用
B.小物体随筒壁做圆周运动的向心力是由摩擦力提供的
C.筒壁对小物体的摩擦力随转速增大而增大
D.筒壁对小物体的弹力随转速增大而增大
答案 D
解析 小物体随转筒一起做圆周运动,受重力、弹力和静摩擦力共3个力的作用,故选项A错误.水平方向上,弹力指向圆心,提供向心力,据牛顿第二定律有:FN=mω2r,又ω=2πn,可知转速越大,角速度越大,小物体所受的弹力就越大,故选项B错误,D正确;在竖直方向上,小物体所受的重力和静摩擦力平衡,静摩擦力大小不变,故选项C错误.
8.(多选)质量为m的小球用长为L的轻质细线悬挂在O点,在O点的正下方处有一光滑小钉子P,把细线沿水平方向拉直,如图7所示,无初速度地释放小球,当细线碰到钉子的瞬间(瞬时速度不变),设细线没有断裂,则下列说法正确的是( )
图7
A.小球的角速度突然增大
B.小球的角速度突然减小
C.小球对细线的拉力突然增大
D.小球对细线的拉力保持不变
答案 AC
解析 根据题意,细线碰到钉子的瞬间,小球的瞬时速度v不变,但其做圆周运动的半径从L突变为,由ω=可知小球的角速度突然增大,选项A正确,B错误;根据FT-mg=m可知小球受到的拉力增大,由牛顿第三定律知,小球对细线的拉力增大,选项C正确,D错误.
9.一质量为m的物体,沿半径为R的半圆形轨道滑行,如图8所示,经过最低点时的速度为v,物体与轨道间的动摩擦因数为μ,重力加速度为g,则它在最低点时受到的摩擦力大小为( )
图8
A.μmg B.
C.μm(g+) D.μm(g-)
答案 C
解析 在最低点由向心力公式得:FN-mg=m,得FN=mg+m,又由摩擦力公式有Ff=μFN=μ(mg+m)=μm(g+),C选项正确.
10.如图9所示,在水平转动的圆盘上,两个完全一样的木块A、B一起随圆盘做匀速圆周运动,转动的角速度为ω,已知木块A、B到圆盘中心O的距离分别为rA和rB,则两木块的向心力之比为( )
图9
A.rA∶rB B.rB∶rA
C.rA2∶rB2 D.rB2∶rA2
解析:选A 木块A、B在绕O点转动的过程中,是木块与圆盘间的静摩擦力提供了木块做匀速圆周运动所需的向心力,因两木块旋转的角速度ω等大,质量一样,由向心力公式Fn=mrω2,得FA=mrAω2,FB=mrBω2,解得FA∶FB=rA∶rB,故A正确。
11.甲、乙两人在光滑的冰面上,面对面拉着弹簧测力计做圆周运动,如图10所示。m甲=80 kg,m乙=40 kg,两人相距0.9 m,弹簧测力计的示数为9.2 N,则下列判断正确的是( )
图10
A.两人的线速度相同,约为40 m/s
B.两人的角速度相同,约为6 rad/s
C.两人的运动半径相同,都是0.45 m
D.两人的运动半径不同,甲为0.3 m,乙为0.6 m
解析:选D 两人做圆周运动的角速度相同,向心力相同,设两人的运动半径分别为r甲和r乙,由向心力公式和圆周运动规律,得m甲r甲ω2=m乙r乙ω2,所以==,又因为r甲+r乙=0.9 m,所以r甲=0.3 m,r乙=0.6 m,C错误,D正确。由v=ωr得两人运动的线速度之比==,A错误。由Fn=m甲r甲ω2,得ω== rad/s≈0.6 rad/s,B错误。
12.如图11所示,把一个长为20 cm、劲度系数为360 N/m的弹簧一端固定,作为圆心,弹簧的另一端连接一个质量为0.50 kg的小球。当小球以 r/min 的转速在光滑水平面上做匀速圆周运动时,弹簧的伸长量应为( )
图11
A.5.2 cm B.5.3 cm
C.5.0 cm D.5.4 cm
解析:选C 小球转动的角速度ω=2nπ=rad/s=12 rad/s,由向心力公式,得kx=mω2(x0+x),解得x== m=0.05 m=5.0 cm,选项C正确。
13.如图12所示,可视为质点的木块A、B叠放在一起,放在水平转台上随转台一起绕固定转轴OO′匀速转动,木块A、B与转轴OO′的距离为1 m,A的质量为5 kg,B的质量为10 kg。已知A与B间的动摩擦因数为0.2,B与转台间的动摩擦因数为0.3,若木块A、B与转台始终保持相对静止,则转台角速度ω的最大值为(最大静摩擦力等于滑动摩擦力,g取10 m/s2)( )
图12
A.1 rad/s B. rad/s
C. rad/s D.3 rad/s
解析:选B 对A有μ1mAg≥mAω2r,对A、B整体有(mA+mB)ω2r≤μ2(mA+mB)g,代入数据解得ω≤ rad/s,故B正确。
14.(多选)如图13所示,在双人花样滑冰运动中,有时会看到被男运动员拉着的女运动员离开地面在空中做圆锥摆运动的精彩场面,目测质量为m的女运动员做圆锥摆运动时和水平冰面的夹角约为30°,运动员转动的周期T=2 s,重力加速度为g,估算可知该女运动员( )
图13
A.受到的拉力为mg
B.受到的拉力为2mg
C.做圆周运动的半径为
D.做圆周运动的半径为
解析:选BC 设女运动员受到的拉力为F,分析女运动员受力情况可知,Fsin 30°=mg,Fcos 30°=mr,解得F=2mg,r=,故B、C正确。
15.(多选)如图14所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则下列说法正确的是( )
图14
A.球A的线速度必定大于球B的线速度
B.球A的角速度必定小于球B的角速度
C.球A的运动周期必定小于球B的运动周期
D.球A对筒壁的压力必定大于球B对筒壁的压力
解析:选AB 两球均贴着圆锥筒的内壁在水平面内做匀速圆周运动,它们均受到重力和筒壁对它们的支持力FN的作用,其合力必定在水平面内时刻指向圆心,如图所示,可知,筒壁对球的支持力FN=,故A、B两球对筒壁的压力大小相等,选项D错误。
由球所受合力提供其做匀速圆周运动的向心力,得mgcot θ=m=mω2r=m,小球的线速度v=,角速度ω= ,周期T=2π 。由此可见,小球的线速度随轨道半径的增大而增大,所以A球的线速度必定大于B球的线速度,选项A正确。小球的角速度随半径的增大而减小,周期随半径的增大而增大,所以A球的角速度小于B球的角速度,A球的周期大于B球的周期,选项B正确,选项C错误。
16.如图15所示,水平转盘的中心有一个光滑的竖直小圆孔,质量为m的物体A放在转盘上,物体A到圆孔的距离为r,物体A通过轻绳与物体B相连,物体B的质量也为m。若物体A与转盘间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,则转盘转动的角速度ω在什么范围内,才能使物体A随转盘转动而不滑动?
图15
解析:当A将要沿转盘背离圆心滑动时,A所受的摩擦力为最大静摩擦力,方向指向圆心,此时A做圆周运动所需的向心力为绳的拉力与最大静摩擦力的合力,即
F+Ffmax=mrω12 ①
由于B静止,故有F=mg ②
又Ffmax=μFN=μmg ③
由①②③式可得ω1=
当A将要沿转盘向圆心滑动时,A所受的摩擦力为最大静摩擦力,方向背离圆心,此时A做圆周运动所需的向心力为
F-Ffmax=mrω22 ④
由②③④式可得ω2=
故要使A随转盘一起转动而不滑动,其角速度ω的范围为ω2≤ω≤ω1,即 ≤ω≤ 。
答案: ≤ω≤
