28.2.1点和圆的位置关系
图片预览





文档简介
(共25张PPT)
点和圆的位置关系
右图是一位射击运动员射击10发子弹的成绩,这一现象体现了平面上的点与圆的位置关系。如何判断点与圆的位置关系呢?
想一想
在平面内点与圆都有哪些位置关系?
圆上、圆外、圆内
那么这三种位置关系中,点到圆心的距离与圆的半径有什么关系?
.
.
.
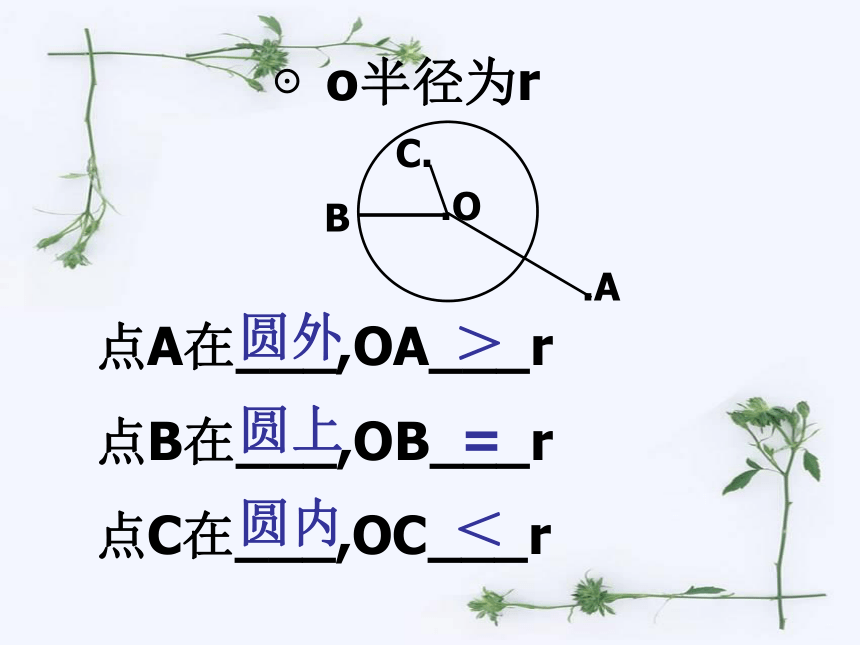
点A在___,OA___r
点B在___,OB___r
点C在___,OC___r
.O
.A
B
C.
⊙o半径为r
圆外
>
圆上
圆内
=
<
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习:已知圆的半径等于5厘米,点到圆心的距离是:
1、8厘米 2、4厘米 3、5厘米。
请你分别说出点与圆的位置关系。
●
●
●
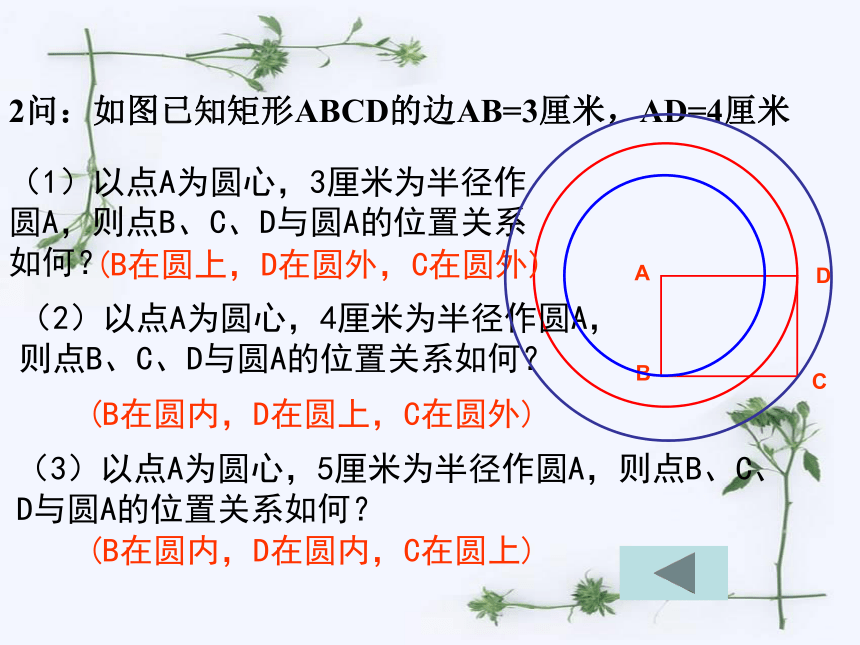
2问:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
☆⊙O的半径r=5cm,圆心O到直线的距离d=OD=3cm。在直线AB上有P、Q、R三点,且有PD=4cm,QD>4cm,RD<4cm。 P、Q、R三点对于⊙O的位置各是怎样的?
做一做
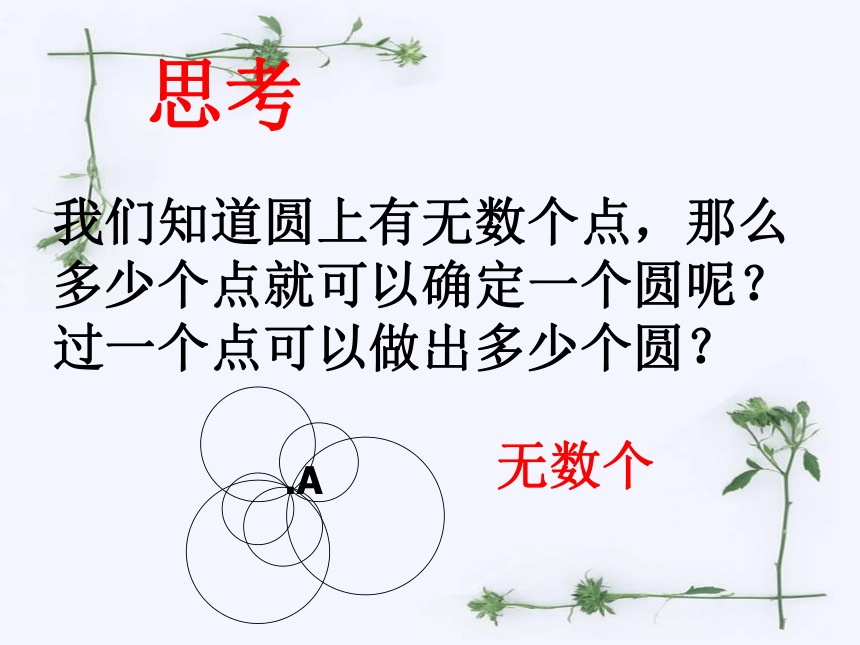
思考
我们知道圆上有无数个点,那么多少个点就可以确定一个圆呢?过一个点可以做出多少个圆?
.A
无数个
到一条线段两个端点距离相等的点在_______________
过两个点能做多少个圆?圆心在哪?
.A
.B
无数个,圆心都在线段AB的垂直平分线上。
这条线段的垂直平分线上
探究(3)1、过同一平面内三个点的情况会怎样呢?
1、不在同一直线上的三点A、B、C。
2、过在同一直线上的三点A、B、C可以作几个圆?
.A
.C
.B
.o
不在同一直线上的三个点确定一个圆,圆心是连结两点的线段垂直平分线的交点。
探究(3)1、过同一平面内三个点的情况会怎样呢?
1、不在同一直线上的三点A、B、C。
2、过在同一直线上的三点A、B、C可以作几个圆?(不能作圆)
一点补充解释
为什么过同在一条直线上的三个点不可以画圆
l
A
B
C
O
a
b
B
A
C
O
阅读,完成以下填空:
如图:⊙O是△ ABC的 圆, △ ABC
是⊙O的 三角形,O是△ ABC的 心,它是 的交点,到
三角形 的距离相等。
外接
内接
外
三角形三边垂直平分线
三个顶点
●
经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆(circumcircle).三角形外接圆的圆心叫做这个三角形的外心(circumcenter).这个三角形叫做这个圆的内接三角形.三角形的外心就是三角形三条边的垂直平分线的交点.
B
A
C
O
●
想一想:
锐角三角形、直角三角 形、钝角三角形的外心各在哪里?
B
●
C
A
B
A
C
·
锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心是三角形斜边的中点。
练习
例1、判断:
1、经过三点一定可以作圆。( )
2、三角形的外心就是这个三角形两边垂直平分线的交点。( )
3、三角形的外心到三边的距离相等。( )
4、经过不在一直线上的四点能作一个圆。( )
×
√
×
×
二、已知Rt△ABC中,∠C=90°,若AC=5cm,BC=12cm,求△ABC的外接圆的半径。
例2、填空:
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )
内部
0﹤r ﹤5
外部
一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
思考
1、过三角形的三个顶点是否都可以作圆?为什么?
2、一个三角形的外接圆有几个?一个圆的内接三角形有几个?为什么?
3、三角形的外心有什么性质?它一定在三角形的内部吗?画图说明。
应用
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
作业
练 习
1. 任意画一个三角形,然后再画这个三角形的外接圆.
2. 随意画出四点,其中任何三点都不在同一条直线上,是否一定可以画一个圆经过这四点?请举例说明.
再 见!
点和圆的位置关系
右图是一位射击运动员射击10发子弹的成绩,这一现象体现了平面上的点与圆的位置关系。如何判断点与圆的位置关系呢?
想一想
在平面内点与圆都有哪些位置关系?
圆上、圆外、圆内
那么这三种位置关系中,点到圆心的距离与圆的半径有什么关系?
.
.
.
点A在___,OA___r
点B在___,OB___r
点C在___,OC___r
.O
.A
B
C.
⊙o半径为r
圆外
>
圆上
圆内
=
<
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习:已知圆的半径等于5厘米,点到圆心的距离是:
1、8厘米 2、4厘米 3、5厘米。
请你分别说出点与圆的位置关系。
●
●
●
2问:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
☆⊙O的半径r=5cm,圆心O到直线的距离d=OD=3cm。在直线AB上有P、Q、R三点,且有PD=4cm,QD>4cm,RD<4cm。 P、Q、R三点对于⊙O的位置各是怎样的?
做一做
思考
我们知道圆上有无数个点,那么多少个点就可以确定一个圆呢?过一个点可以做出多少个圆?
.A
无数个
到一条线段两个端点距离相等的点在_______________
过两个点能做多少个圆?圆心在哪?
.A
.B
无数个,圆心都在线段AB的垂直平分线上。
这条线段的垂直平分线上
探究(3)1、过同一平面内三个点的情况会怎样呢?
1、不在同一直线上的三点A、B、C。
2、过在同一直线上的三点A、B、C可以作几个圆?
.A
.C
.B
.o
不在同一直线上的三个点确定一个圆,圆心是连结两点的线段垂直平分线的交点。
探究(3)1、过同一平面内三个点的情况会怎样呢?
1、不在同一直线上的三点A、B、C。
2、过在同一直线上的三点A、B、C可以作几个圆?(不能作圆)
一点补充解释
为什么过同在一条直线上的三个点不可以画圆
l
A
B
C
O
a
b
B
A
C
O
阅读,完成以下填空:
如图:⊙O是△ ABC的 圆, △ ABC
是⊙O的 三角形,O是△ ABC的 心,它是 的交点,到
三角形 的距离相等。
外接
内接
外
三角形三边垂直平分线
三个顶点
●
经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆(circumcircle).三角形外接圆的圆心叫做这个三角形的外心(circumcenter).这个三角形叫做这个圆的内接三角形.三角形的外心就是三角形三条边的垂直平分线的交点.
B
A
C
O
●
想一想:
锐角三角形、直角三角 形、钝角三角形的外心各在哪里?
B
●
C
A
B
A
C
·
锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心是三角形斜边的中点。
练习
例1、判断:
1、经过三点一定可以作圆。( )
2、三角形的外心就是这个三角形两边垂直平分线的交点。( )
3、三角形的外心到三边的距离相等。( )
4、经过不在一直线上的四点能作一个圆。( )
×
√
×
×
二、已知Rt△ABC中,∠C=90°,若AC=5cm,BC=12cm,求△ABC的外接圆的半径。
例2、填空:
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )
内部
0﹤r ﹤5
外部
一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
思考
1、过三角形的三个顶点是否都可以作圆?为什么?
2、一个三角形的外接圆有几个?一个圆的内接三角形有几个?为什么?
3、三角形的外心有什么性质?它一定在三角形的内部吗?画图说明。
应用
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
作业
练 习
1. 任意画一个三角形,然后再画这个三角形的外接圆.
2. 随意画出四点,其中任何三点都不在同一条直线上,是否一定可以画一个圆经过这四点?请举例说明.
再 见!
