勾股定理的应用 PPT课件 八年级数学 初二课件
文档属性
| 名称 | 勾股定理的应用 PPT课件 八年级数学 初二课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-31 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
勾股定理的应用
武乡二中 张小平
【知识与技能】掌握勾股定理在现实生活中的应用。
【过程与方法】经历把实际问题转化成数学问题,利用勾股定理解决的过程。
【情感、态度与价值观】培养学生良好的学习习惯、合作交流的学习方法、以及学数学、用数学的乐趣。
学习目标
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
知识回味
请同学们完成下面的练习
1、在直角 三角形 ABC中,两条直角边a,b分别等于6和8,则斜边c等于( )。
2、直角三角形一直角边为9cm,斜边为15cm,则这个直角三角形的面积为( )cm2 。
3、一个等腰三角形的腰长为20cm,底边长为24cm,则底边上的高为( )cm,面积为( )cm2 。
10
课前热身
54
16
192
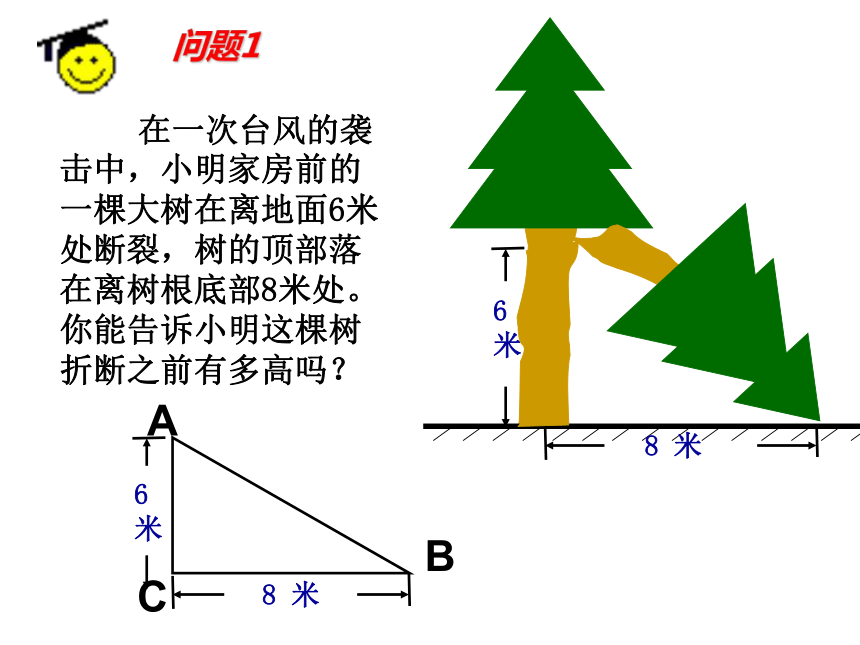
在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
问题1
8 米
6米
A
C
B
6米
8 米
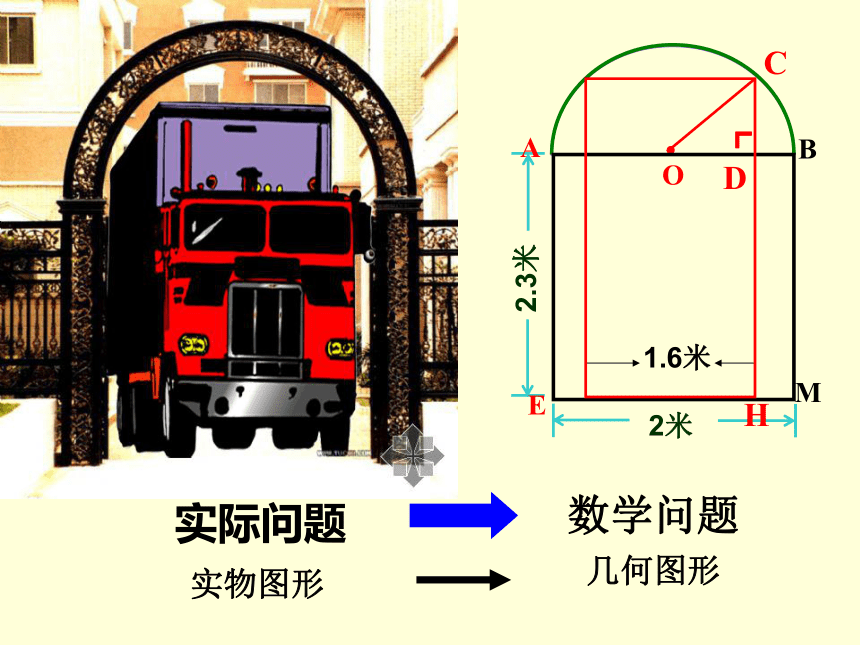
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由
问题二
帮卡车司机排忧解难。
2.3米
2米
1.6米
A
B
M
E
O
┏
C
D
H
实际问题
数学问题
实物图形
几何图形
A
B
M
E
O
C
┏
D
H
2米
2.3米
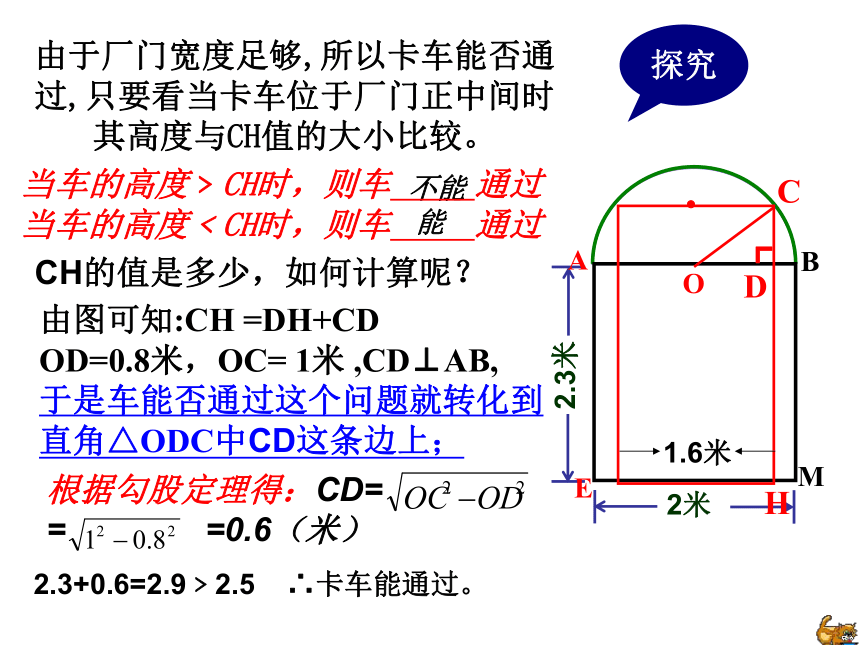
由图可知:CH =DH+CD OD=0.8米,OC= 1米 ,CD⊥AB, 于是车能否通过这个问题就转化到直角△ODC中CD这条边上;
探究
不能
能
由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度与CH值的大小比较。
当车的高度﹥CH时,则车 通过 当车的高度﹤CH时,则车 通过
1.6米
根据勾股定理得:CD= = =0.6(米)
2.3+0.6=2.9﹥2.5 ∴卡车能通过。
CH的值是多少,如何计算呢?
一位工人叔叔要装修家,需要一块长3m、宽2.1m的薄木板,已知他家门框的尺寸如图所示,那么这块薄木板能否从门框内通过 为什么
1m
2m
挑战“试一试”:
实际问题
猜一猜
一个门框的尺寸如图所示,一块长3m、宽2.1m的薄木板能否从门框内通过
1m
2m
(A) 能
(B) 不能
(C) 不确定
√
√
√
门框的尺寸,薄木板的尺寸如图所示,薄木板能否从门框内通过 ( ≈2.236)
思考
1m
2m
A
D
C
B
2.1米
3米
门框的尺寸,薄木板的尺寸如图所示,薄木板能否从门框内通过 ( ≈2.236)
思考
1m
2m
A
D
C
B
2.1米
3米
一个门框的尺寸如图所示,一块长3m、宽2.1m的薄木板能否从门框内通过 为什么
1m
2m
解答
A
D
C
B
解:联结AC,在Rt△ABC中AB=2m, BC=1m ∠B=90°,根据勾股定理:
>2.1m
∴薄木板能从门框内通过。
1. 如图,公园内有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设3步为1米),却踩伤了花草.
超越自我
3m
4m
路
回顾本节课,我们运用勾股定理如何解决实际问题?
你有什么收获?
小结
2.注意:运用勾股定理解决实际问题,关键在于“找”到合适的直角三角形.
小 结
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
1.
作业
1. 必做题: X课本P53练习第1题 P54第3题.
2. 选做题: 《练习册》P82第2 , 3题 .
课后探究:
如图,以直角三角形ABC的三边为边分别向外作正方形,其中一个正方形划分成四个形状和大小都一样的四边形,试将图中5个带色的图形拼入到大正方形中,填满整个大正方形。
B
C
A
再 见
1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
解设AC的长为 X 米,
则AB=(x+1)米
过关斩将
勾股定理的应用
武乡二中 张小平
【知识与技能】掌握勾股定理在现实生活中的应用。
【过程与方法】经历把实际问题转化成数学问题,利用勾股定理解决的过程。
【情感、态度与价值观】培养学生良好的学习习惯、合作交流的学习方法、以及学数学、用数学的乐趣。
学习目标
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
知识回味
请同学们完成下面的练习
1、在直角 三角形 ABC中,两条直角边a,b分别等于6和8,则斜边c等于( )。
2、直角三角形一直角边为9cm,斜边为15cm,则这个直角三角形的面积为( )cm2 。
3、一个等腰三角形的腰长为20cm,底边长为24cm,则底边上的高为( )cm,面积为( )cm2 。
10
课前热身
54
16
192
在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
问题1
8 米
6米
A
C
B
6米
8 米
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由
问题二
帮卡车司机排忧解难。
2.3米
2米
1.6米
A
B
M
E
O
┏
C
D
H
实际问题
数学问题
实物图形
几何图形
A
B
M
E
O
C
┏
D
H
2米
2.3米
由图可知:CH =DH+CD OD=0.8米,OC= 1米 ,CD⊥AB, 于是车能否通过这个问题就转化到直角△ODC中CD这条边上;
探究
不能
能
由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度与CH值的大小比较。
当车的高度﹥CH时,则车 通过 当车的高度﹤CH时,则车 通过
1.6米
根据勾股定理得:CD= = =0.6(米)
2.3+0.6=2.9﹥2.5 ∴卡车能通过。
CH的值是多少,如何计算呢?
一位工人叔叔要装修家,需要一块长3m、宽2.1m的薄木板,已知他家门框的尺寸如图所示,那么这块薄木板能否从门框内通过 为什么
1m
2m
挑战“试一试”:
实际问题
猜一猜
一个门框的尺寸如图所示,一块长3m、宽2.1m的薄木板能否从门框内通过
1m
2m
(A) 能
(B) 不能
(C) 不确定
√
√
√
门框的尺寸,薄木板的尺寸如图所示,薄木板能否从门框内通过 ( ≈2.236)
思考
1m
2m
A
D
C
B
2.1米
3米
门框的尺寸,薄木板的尺寸如图所示,薄木板能否从门框内通过 ( ≈2.236)
思考
1m
2m
A
D
C
B
2.1米
3米
一个门框的尺寸如图所示,一块长3m、宽2.1m的薄木板能否从门框内通过 为什么
1m
2m
解答
A
D
C
B
解:联结AC,在Rt△ABC中AB=2m, BC=1m ∠B=90°,根据勾股定理:
>2.1m
∴薄木板能从门框内通过。
1. 如图,公园内有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设3步为1米),却踩伤了花草.
超越自我
3m
4m
路
回顾本节课,我们运用勾股定理如何解决实际问题?
你有什么收获?
小结
2.注意:运用勾股定理解决实际问题,关键在于“找”到合适的直角三角形.
小 结
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
1.
作业
1. 必做题: X课本P53练习第1题 P54第3题.
2. 选做题: 《练习册》P82第2 , 3题 .
课后探究:
如图,以直角三角形ABC的三边为边分别向外作正方形,其中一个正方形划分成四个形状和大小都一样的四边形,试将图中5个带色的图形拼入到大正方形中,填满整个大正方形。
B
C
A
再 见
1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
解设AC的长为 X 米,
则AB=(x+1)米
过关斩将
