十六章 分式复习 PPT课件 八年级数学 初二课件
文档属性
| 名称 | 十六章 分式复习 PPT课件 八年级数学 初二课件 |  | |
| 格式 | rar | ||
| 文件大小 | 398.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-31 10:59:00 | ||
图片预览






文档简介
(共19张PPT)
十六章 分式复习
临沂凤凰岭中学 邢志涛
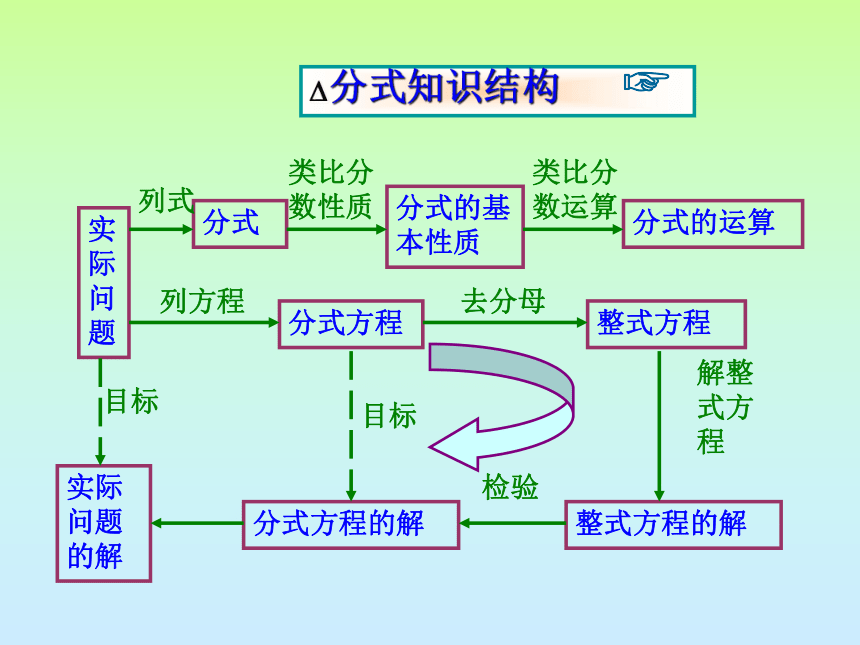
实际问题
分式
分式的基本性质
分式的运算
列式
列方程
分式方程
去分母
整式方程
解整式方程
整式方程的解
分式方程的解
实际问题的解
目标
目标
分式知识结构
类比分数性质
类比分数运算
检验
2、分式的加减法则:
3、分式的乘除法则:
4、分式的乘方法则:
1、形如 的式子叫做分式,其中A、B是整式,B中必须含有字母。对于任意一个分式,分母都不能为零。
例1、下列各有理式中,哪些是分式?哪些是整式?
试一试
分式的定义
解:由 m – 3 ≠0,得 m≠3。所以当 m≠3 时,
分式有意义;
由 m2 – 9 =0,得 m=±3。而当 m=3 时,分母
m – 3 =0,分式没有意义,故应舍去,
所以当 m= - 3时,分式的值为零。
例2:当 m 取何值时,分式 有意义?
值为零?
分式有无意义与什么有关?
分式有无意义只与分母有关
变式练习
例3、计算:
解:
分式的加减
( A)扩大5倍
( B)扩大15倍
( C)不变
( D)是原来的
C
思考:如果把分式 中x、y都扩大5倍,则分式的值如何变化?
同步练习
例4:解方程
解:方程两边都乘以 (x+1) ( x – 1 ) , 约去分母,得
( x + 1 )2-4 = x2-1
解这个整式方程,得
x = 1
经检验得:分母 x -1 =O
∴原方程无解.
解分式方程的一般步骤
1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
解分式方程的思路是:
分式方程
整式方程
去分母
一化二解三检验
变式练习 解分式方程
思维误区分析:
1、确定最简公分母失误;
2、去分母时漏乘整数项;
3、去分母时忽略符号的变化;
4、忘记验根。
例5:甲乙两队人员搬运一些电力器材上山,甲队单独完成任务比乙队单独完成任务少用50分钟,若甲、乙两队一起搬运1小时可以完成,问甲、乙两队单独搬运,各需几分钟完成?
工作效率 工作时间 工作量
甲
乙
1/x
1/(x+50)
60
60
60/x
60/(X+50)
甲完成的工作量+乙完成的工作量=工作总量
工程问题
例6、甲、乙两地相距150千米,一轮船从甲地逆流航行至乙地,然后又从乙地返回甲地,已知水流的速度为3千米/时,回来时所用的时间是去时的四分之三,求轮船在静水中的速度。
解:设轮船在静水中的速度为x千米/时
x=21
路程 速度 时间
逆流
顺流
150
150
X-3
3
行程问题
经检验,x=21是原方程的解。
例7、甲加工180个零件所用的时间,乙可以加工240个零件,已知甲每小时比乙少加工5个零件,求两人每小时各加工的零件个数.
实际问题
解:设甲每小时加工x个零件,则乙每小时加工(x+5)个零件,根据题意得:
解得 x=15
经检验x=15是原方程的解
1、列分式方程解应用题,应该注意解题的五个步骤。
2、列方程的关键是要在准确设元(可直接设,也可间接设)的前提下找出等量关系。
3、解题过程注意画图或列表帮助分析题意找等量关系。
4、注意不要漏检验和写答案。
请同学总结列分式方程应注意的问题
1、某工人师傅先后两次加工零件各1500个,当第二次加工时,他革新了工具,改进了操作方法,结果比第一次少用了18个小时.已知他第二次加工效率是第一次的2.5倍,求他第二次加工时每小时加工多少零件
变式训练
2、某人骑自行车比步行每小时多走8千米,如果他步行12千米所用时间与骑车行36千米所用的时间相等,求他步行40千米用多少小时
1.通过本节课的学习,你在知识上有什么收获?还有哪些困惑?
2.在思想方法上有哪些收获?
2.你对自己本节课的表现满意吗?为什么?
十六章 分式复习
临沂凤凰岭中学 邢志涛
实际问题
分式
分式的基本性质
分式的运算
列式
列方程
分式方程
去分母
整式方程
解整式方程
整式方程的解
分式方程的解
实际问题的解
目标
目标
分式知识结构
类比分数性质
类比分数运算
检验
2、分式的加减法则:
3、分式的乘除法则:
4、分式的乘方法则:
1、形如 的式子叫做分式,其中A、B是整式,B中必须含有字母。对于任意一个分式,分母都不能为零。
例1、下列各有理式中,哪些是分式?哪些是整式?
试一试
分式的定义
解:由 m – 3 ≠0,得 m≠3。所以当 m≠3 时,
分式有意义;
由 m2 – 9 =0,得 m=±3。而当 m=3 时,分母
m – 3 =0,分式没有意义,故应舍去,
所以当 m= - 3时,分式的值为零。
例2:当 m 取何值时,分式 有意义?
值为零?
分式有无意义与什么有关?
分式有无意义只与分母有关
变式练习
例3、计算:
解:
分式的加减
( A)扩大5倍
( B)扩大15倍
( C)不变
( D)是原来的
C
思考:如果把分式 中x、y都扩大5倍,则分式的值如何变化?
同步练习
例4:解方程
解:方程两边都乘以 (x+1) ( x – 1 ) , 约去分母,得
( x + 1 )2-4 = x2-1
解这个整式方程,得
x = 1
经检验得:分母 x -1 =O
∴原方程无解.
解分式方程的一般步骤
1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
解分式方程的思路是:
分式方程
整式方程
去分母
一化二解三检验
变式练习 解分式方程
思维误区分析:
1、确定最简公分母失误;
2、去分母时漏乘整数项;
3、去分母时忽略符号的变化;
4、忘记验根。
例5:甲乙两队人员搬运一些电力器材上山,甲队单独完成任务比乙队单独完成任务少用50分钟,若甲、乙两队一起搬运1小时可以完成,问甲、乙两队单独搬运,各需几分钟完成?
工作效率 工作时间 工作量
甲
乙
1/x
1/(x+50)
60
60
60/x
60/(X+50)
甲完成的工作量+乙完成的工作量=工作总量
工程问题
例6、甲、乙两地相距150千米,一轮船从甲地逆流航行至乙地,然后又从乙地返回甲地,已知水流的速度为3千米/时,回来时所用的时间是去时的四分之三,求轮船在静水中的速度。
解:设轮船在静水中的速度为x千米/时
x=21
路程 速度 时间
逆流
顺流
150
150
X-3
3
行程问题
经检验,x=21是原方程的解。
例7、甲加工180个零件所用的时间,乙可以加工240个零件,已知甲每小时比乙少加工5个零件,求两人每小时各加工的零件个数.
实际问题
解:设甲每小时加工x个零件,则乙每小时加工(x+5)个零件,根据题意得:
解得 x=15
经检验x=15是原方程的解
1、列分式方程解应用题,应该注意解题的五个步骤。
2、列方程的关键是要在准确设元(可直接设,也可间接设)的前提下找出等量关系。
3、解题过程注意画图或列表帮助分析题意找等量关系。
4、注意不要漏检验和写答案。
请同学总结列分式方程应注意的问题
1、某工人师傅先后两次加工零件各1500个,当第二次加工时,他革新了工具,改进了操作方法,结果比第一次少用了18个小时.已知他第二次加工效率是第一次的2.5倍,求他第二次加工时每小时加工多少零件
变式训练
2、某人骑自行车比步行每小时多走8千米,如果他步行12千米所用时间与骑车行36千米所用的时间相等,求他步行40千米用多少小时
1.通过本节课的学习,你在知识上有什么收获?还有哪些困惑?
2.在思想方法上有哪些收获?
2.你对自己本节课的表现满意吗?为什么?
