28.1锐角三角函数(2)正切 PPT课件 新人教版九年级数学下册 初三课件
文档属性
| 名称 | 28.1锐角三角函数(2)正切 PPT课件 新人教版九年级数学下册 初三课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 841.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-31 10:59:00 | ||
图片预览



文档简介
(共15张PPT)
新人教版九年级数学(下册)第二十八章
惕安中学 郑金洲
§28.1 锐角三角函数(2)
——正切
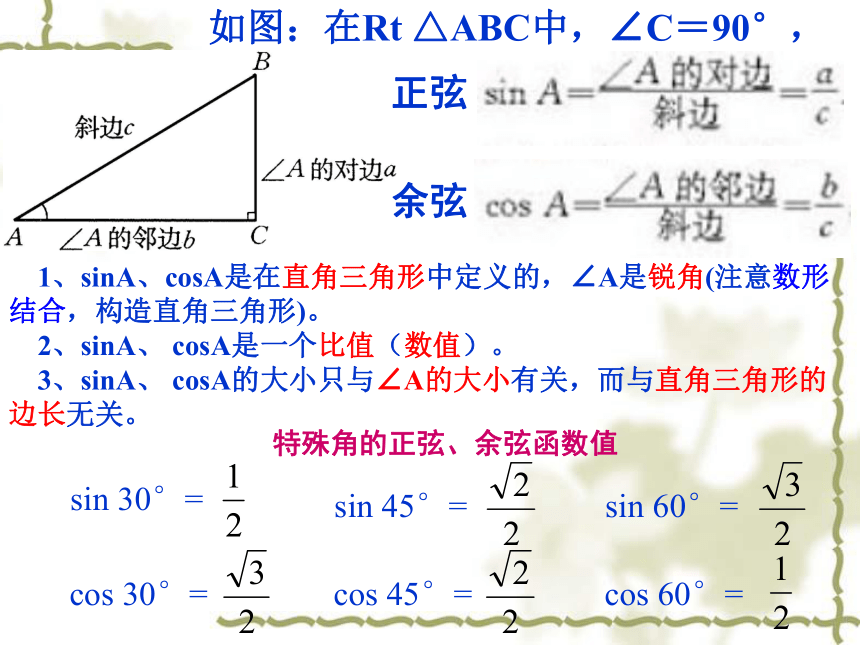
1、sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA是一个比值(数值)。
3、sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
如图:在Rt △ABC中,∠C=90°,
sin 30°=
sin 45°=
sin 60°=
cos 30°=
cos 45°=
cos 60°=
特殊角的正弦、余弦函数值
正弦
余弦
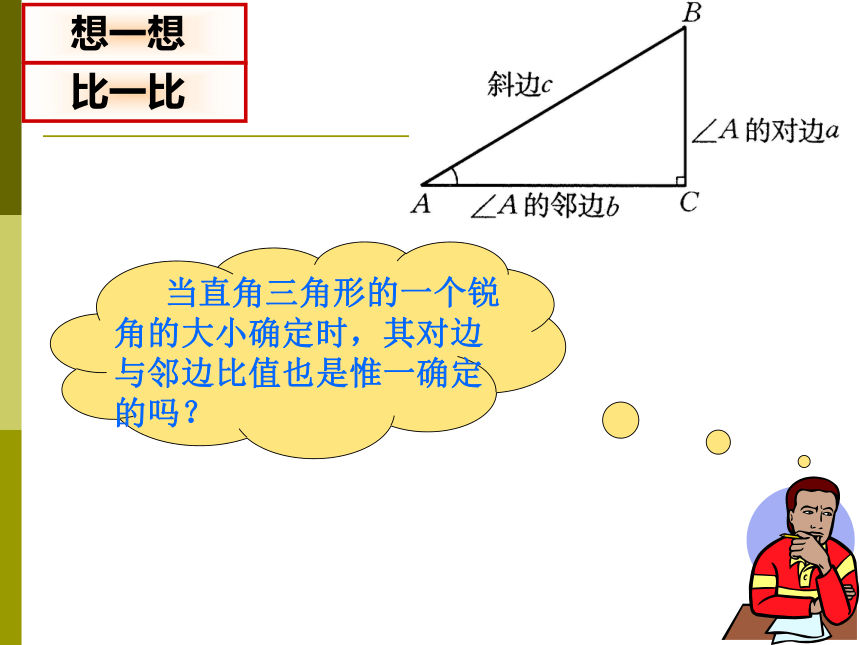
当直角三角形的一个锐角的大小确定时,其对边与邻边比值也是惟一确定的吗?
想一想
比一比
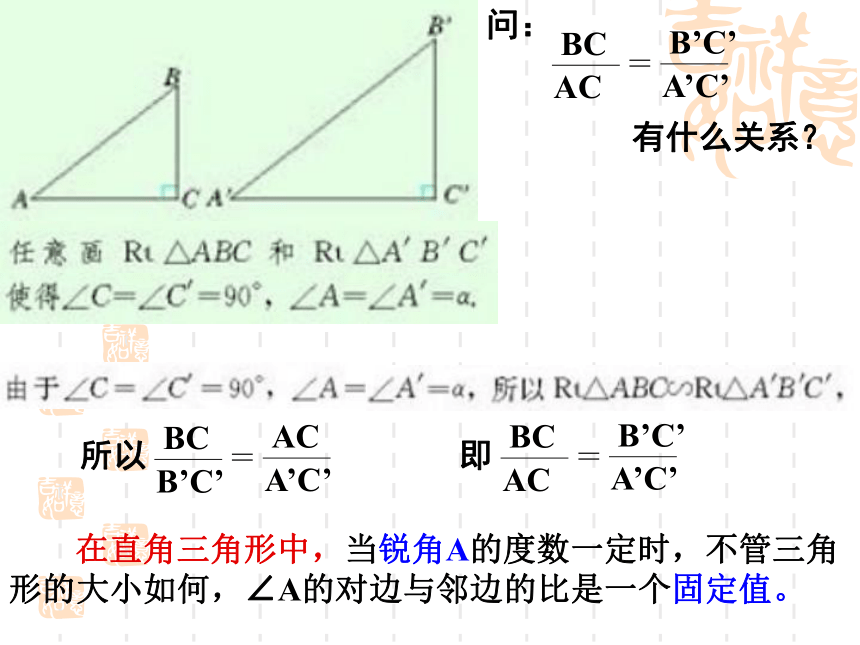
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值。
B’C’
BC
A’C’
AC
=
所以
AC
BC
A’C’
B’C’
=
即
AC
BC
A’C’
B’C’
=
问:
有什么关系?
如图:在Rt △ABC中,∠C=90°,
我们把锐角A的对边与邻边的比叫做∠A的 正切,记作 tanA。
一个角的正切表示定值、比值、正值。
tan30°=
A
B
C
┌
思考:锐角A的正切值可以等于1吗?为什么?
可以大于1吗?
对于锐角A的每一个确定的值,sinA、cosA、tanA都有唯一的确定的值与它对应,所以把锐角A的正弦、余弦、正切叫做∠A的锐角三角函数。
tan 45°=
tan 60°=
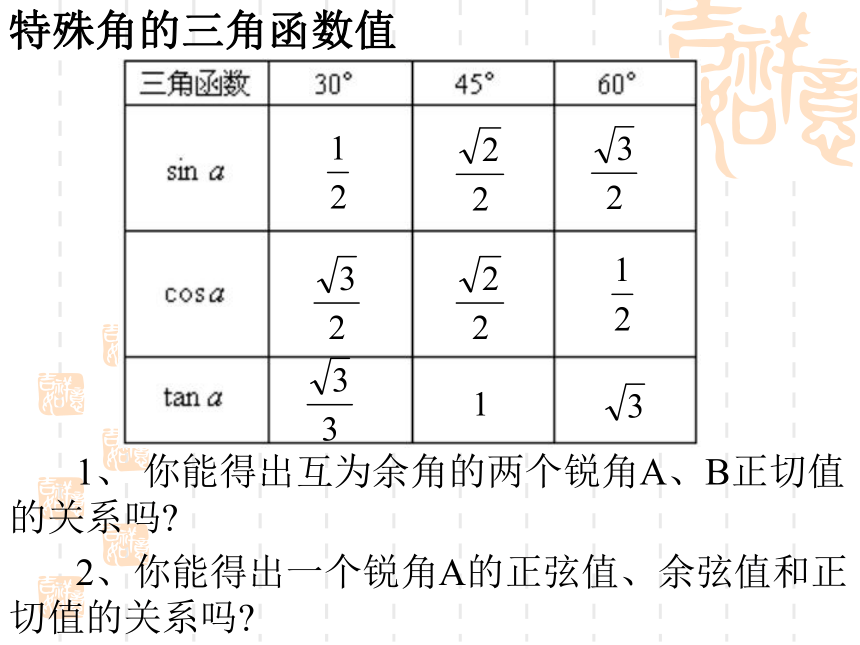
特殊角的三角函数值
1、 你能得出互为余角的两个锐角A、B正切值的关系吗
2、你能得出一个锐角A的正弦值、余弦值和正切值的关系吗
应用举例
1、在Rt △ABC中,∠C=90°,求∠A的三角函数值。
① a=9 b=12
② a=9 b=12
2、在△ABC中,AB=AC=4,BC=6,求∠B的三角函数值。
3、已知∠A为锐角,sinA= ,求cosA、tanA的值。
八仙过海,尽显才能
随堂练习
下图中∠ACB=90°,CD⊥AB,垂足为D。指出∠A和∠B的对边、邻边。
试一试:
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
试一试:
=
a
c
sinA=
小结 回顾
在Rt△ABC中
及时总结经验,要养成积累方法和经验的良好习惯!
=
b
c
cosA=
=
a
b
tanA=
定义中应该注意的几个问题:
回味 无穷
1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA、tanA是一个比值(数值)。
3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
课时作业本
P76—P83
课后作业
独立完成作业的良好习惯,是成长过程中的良师益友。
中考语录
中考是一场跳高比赛,取胜关键在于你起跳时对大地用力多少!
结束寄语
业精于勤而荒于嬉
新人教版九年级数学(下册)第二十八章
惕安中学 郑金洲
§28.1 锐角三角函数(2)
——正切
1、sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA是一个比值(数值)。
3、sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
如图:在Rt △ABC中,∠C=90°,
sin 30°=
sin 45°=
sin 60°=
cos 30°=
cos 45°=
cos 60°=
特殊角的正弦、余弦函数值
正弦
余弦
当直角三角形的一个锐角的大小确定时,其对边与邻边比值也是惟一确定的吗?
想一想
比一比
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值。
B’C’
BC
A’C’
AC
=
所以
AC
BC
A’C’
B’C’
=
即
AC
BC
A’C’
B’C’
=
问:
有什么关系?
如图:在Rt △ABC中,∠C=90°,
我们把锐角A的对边与邻边的比叫做∠A的 正切,记作 tanA。
一个角的正切表示定值、比值、正值。
tan30°=
A
B
C
┌
思考:锐角A的正切值可以等于1吗?为什么?
可以大于1吗?
对于锐角A的每一个确定的值,sinA、cosA、tanA都有唯一的确定的值与它对应,所以把锐角A的正弦、余弦、正切叫做∠A的锐角三角函数。
tan 45°=
tan 60°=
特殊角的三角函数值
1、 你能得出互为余角的两个锐角A、B正切值的关系吗
2、你能得出一个锐角A的正弦值、余弦值和正切值的关系吗
应用举例
1、在Rt △ABC中,∠C=90°,求∠A的三角函数值。
① a=9 b=12
② a=9 b=12
2、在△ABC中,AB=AC=4,BC=6,求∠B的三角函数值。
3、已知∠A为锐角,sinA= ,求cosA、tanA的值。
八仙过海,尽显才能
随堂练习
下图中∠ACB=90°,CD⊥AB,垂足为D。指出∠A和∠B的对边、邻边。
试一试:
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
试一试:
=
a
c
sinA=
小结 回顾
在Rt△ABC中
及时总结经验,要养成积累方法和经验的良好习惯!
=
b
c
cosA=
=
a
b
tanA=
定义中应该注意的几个问题:
回味 无穷
1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA、tanA是一个比值(数值)。
3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
课时作业本
P76—P83
课后作业
独立完成作业的良好习惯,是成长过程中的良师益友。
中考语录
中考是一场跳高比赛,取胜关键在于你起跳时对大地用力多少!
结束寄语
业精于勤而荒于嬉
