2020-2021学年黑龙江省哈尔滨市道里区九年级(上)期末数学试卷(五四学制) (Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市道里区九年级(上)期末数学试卷(五四学制) (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 05:58:02 | ||
图片预览




文档简介
2020-2021学年黑龙江省哈尔滨市道里区九年级第一学期期末数学试卷(五四学制)
一.选择题(共10小题).
1.下列各点中,在反比例函数y=图象上的是( )
A.(﹣1,8) B.(﹣2,4) C.(1,7) D.(2,4)
2.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
3.袋子中装有4个黑球、2个白球,这些球的形状、大小、质地完全相同,即除颜色外无其他差别.在看不到球的条件下,随机从袋中摸出1个球,是白球的概率是( )
A. B. C. D.
4.下面四个几何体中,主视图为三角形的是( )
A. B.
C. D.
5.把函数y=(x﹣1)2+2图象向右平移1个单位长度,平移后图象的函数解析式为( )
A.y=x2+2 B.y=(x﹣1)2+1 C.y=(x﹣2)2+2 D.y=(x﹣1)2﹣3
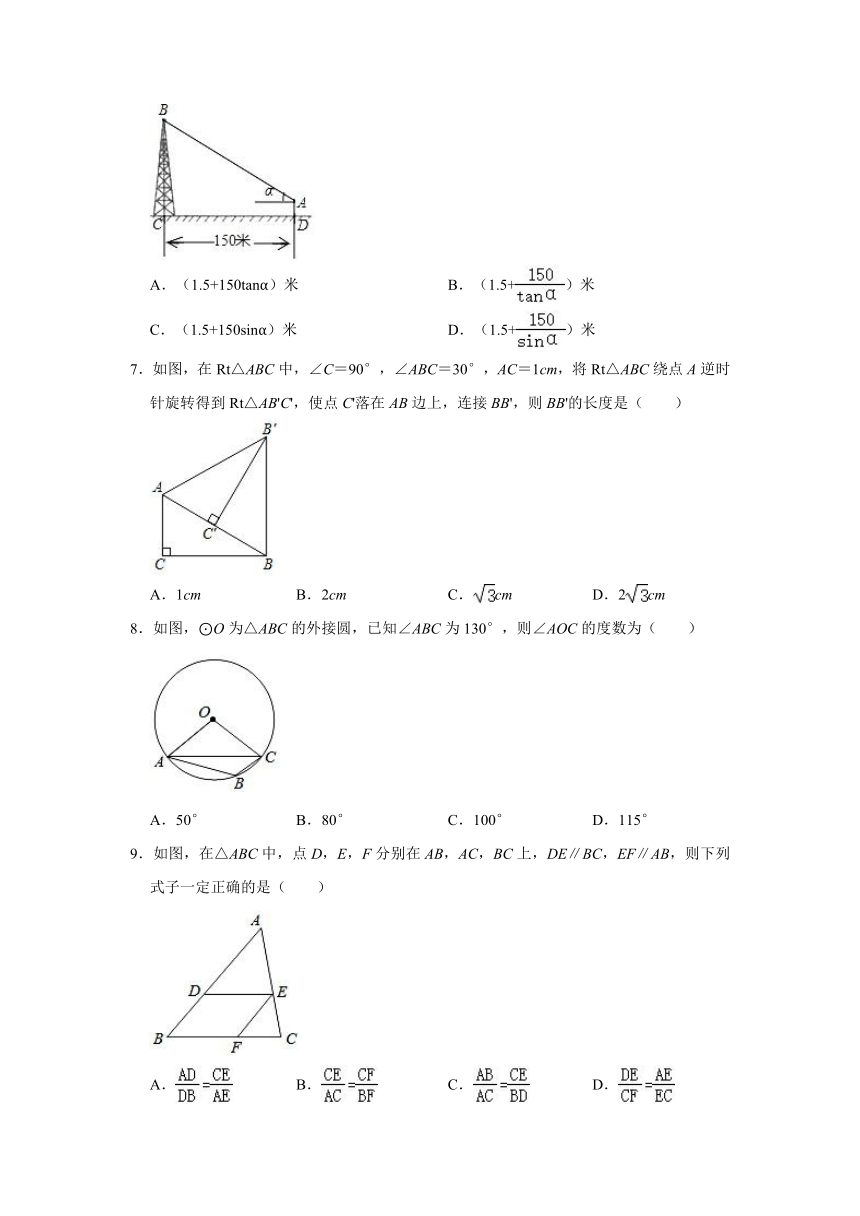
6.如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
A.(1.5+150tanα)米 B.(1.5+)米
C.(1.5+150sinα)米 D.(1.5+)米
7.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长度是( )
A.1cm B.2cm C.cm D.2cm
8.如图,⊙O为△ABC的外接圆,已知∠ABC为130°,则∠AOC的度数为( )
A.50° B.80° C.100° D.115°
9.如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,则下列式子一定正确的是( )
A. B. C. D.
10.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:
①abc<0;
②4a﹣2b+c=0;
③当x>1时,y随x的增大而增大;
④关于x的一元二次方程ax2+bx+c=0有一个实数根.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共10小题).
11.在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是 .
12.抛物线y=2(x+1)2﹣3的顶点坐标为 .
13.一辆汽车行驶的路程s(单位:m)关于时间t(单位:s)的函数解析式是s=9t+t2,经过16s汽车行驶了 m.
14.反比例函数y=的图象经过点(﹣2,3),则k的值为 .
15.如图,AD是△ABC的外接圆⊙O的直径,若∠BAD=40°,则∠ACB= °.
16.在△ABC中,∠C=90°,sinA=,BC=6,则AC的长为 .
17.若扇形的圆心角为45°,半径为6,则该扇形的弧长为 .
18.AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若△AOM中有一个角是30°,OM=3,则弦AB的长为 .
19.同时掷两个质地均匀的骰子,则两个骰子的点数和是10的概率为 .
20.如图,△ABC的中线AD与高CE交于点F,AE=EF,FD=2,S△ACF=24,则AB的长为 .
三、解答题(60分)
21.先化简,再求代数式(1+)÷值,其中x=3tan30°.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图中画出等腰△ABC,点C在小正方形顶点上;
(2)在(1)的条件下确定点C后,再确定点D,点D在小正方形顶点上,请你连接DA,DC,DB,使tan∠ACD=,并直接写出四边形ADBC的面积为 .
23.为了解疫情期间学生网络学习的学习效果,高远中学随机抽取了部分学生进行调查.要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果.现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题
(1)这次活动共抽查学生多少名?
(2)请通过计算补全条形统计图;
(3)若高远中学共有1600名学生,估计该中学“优秀”等次的学生有多少名?
24.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.
(1)求证:CF=AF;
(2)在不添加任何辅助线的情况下,请直接写出图中所有的等腰直角三角形.
25.某班班主任对在某次考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,若购买甲种笔记本15个,乙种笔记本20个,共花费250元;若购买甲种笔记本10个,乙种笔记本25个,共花费225元.
(1)求购买一个甲种、一个乙种笔记本各需多少元?
(2)班主任决定再次购买甲、乙两种笔记本共35个,如果班主任此次购买甲、乙两种笔记本的总费用不超过300元,求至多需要购买多少个甲种笔记本?
26.△ABC内接于⊙O,CA=CB,BD为⊙O的直径,∠DBC=30°.
(1)如图1,求证:△ABC为等边三角形;
(2)如图2,弦AE交BC于点F,点G在EC上,∠BAF=∠GAF,求证:FB=FG;
(3)如图3,在(2)的条件下,弦BH分别交AF,AG于P,Q两点,PO=DH=,AC=3,求QG的长.
27.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx﹣3交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C,OB=OC=OA.
(1)如图1,求抛物线的解析式;
(2)如图2,点D在抛物线上,且点D在第二象限,连接BD交y轴于点E,若tan∠EBA=,求点D的坐标;
(3)如图3,在(2)的条件下,点P在抛物线上,且点P在第三象限,点F在PB上,FC=FB,过点F作x轴的垂线,点G为垂足,连接DG并延长交BF于点H,若∠DHP=∠CEB,求BP的长.
参考答案
一.选择题(共10小题).
1.下列各点中,在反比例函数y=图象上的是( )
A.(﹣1,8) B.(﹣2,4) C.(1,7) D.(2,4)
解:A、∵﹣1×8=﹣8≠8,∴该点不在函数图象上,故本选项错不合题意;
B、∵﹣2×4=﹣8≠8,∴该点不在函数图象上,故本选项不合题意;
C、∵1×7=7≠8,∴该点不在函数图象上,故本选项不合题意;
D、2×4=8,∴该点在函数图象上,故本选项符合题意.
故选:D.
2.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.
解:A、既不是轴对称图形,也不是中心对称图形,故本选项不合题意;
B、不是轴对称图形,是中心对称图形,故本选项不合题意;
C、是轴对称图形,不是中心对称图形,故本选项不合题意;
D、既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
3.袋子中装有4个黑球、2个白球,这些球的形状、大小、质地完全相同,即除颜色外无其他差别.在看不到球的条件下,随机从袋中摸出1个球,是白球的概率是( )
A. B. C. D.
【分析】用白球的个数除以总球的个数即可得出答案.
解:∵袋子中装有4个黑球、2个白球,共有6个球,
∴随机从袋中摸出1个球,是白球的概率是=.
故选:A.
4.下面四个几何体中,主视图为三角形的是( )
A. B.
C. D.
【分析】根据主视图是从正面看得到的图形,可得答案.
解:A、主视图是圆,故A不符合题意;
B、主视图是三角形,故B符合题意;
C、主视图是矩形,故C不符合题意;
D、主视图是正方形,故D不符合题意;
故选:B.
5.把函数y=(x﹣1)2+2图象向右平移1个单位长度,平移后图象的函数解析式为( )
A.y=x2+2 B.y=(x﹣1)2+1 C.y=(x﹣2)2+2 D.y=(x﹣1)2﹣3
解:二次函数y=(x﹣1)2+2的图象的顶点坐标为(1,2),
∴向右平移1个单位长度后的函数图象的顶点坐标为(2,2),
∴所得的图象解析式为y=(x﹣2)2+2.
故选:C.
6.如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
A.(1.5+150tanα)米 B.(1.5+)米
C.(1.5+150sinα)米 D.(1.5+)米
【分析】过点A作AE⊥BC,E为垂足,再由锐角三角函数的定义求出BE的长,由BC=CE+BE即可得出结论.
解:过点A作AE⊥BC,E为垂足,如图所示:
则四边形ADCE为矩形,AE=150,
∴CE=AD=1.5,
在△ABE中,∵tanα==,
∴BE=150tanα,
∴BC=CE+BE=(1.5+150tanα)(m),
故选:A.
7.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长度是( )
A.1cm B.2cm C.cm D.2cm
【分析】由直角三角形的性质得到AB=2AC=2,然后根据旋转的性质和线段垂直平分线的性质得到AB′=BB′.
解:∵在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1cm,
∴AC=AB,则AB=2AC=2cm.
又由旋转的性质知,AC′=AC=AB,B′C′⊥AB,
∴B′C′是△ABB′的中垂线,
∴AB′=BB′.
根据旋转的性质知AB=AB′=BB′=2cm.
故选:B.
8.如图,⊙O为△ABC的外接圆,已知∠ABC为130°,则∠AOC的度数为( )
A.50° B.80° C.100° D.115°
解:作所对的圆周角∠ADC,如图,
∵∠ADC+∠ABC=180°,
而∠ABC=130°,
∴∠ADC=180°﹣130°=50°,
∴∠AOC=2∠ADC=100°.
故选:C.
9.如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,则下列式子一定正确的是( )
A. B. C. D.
【分析】根据平行线分线段成比例可对A选项和B选项进行判断;:利用DE∥BC得到=,则根据比例的性质可对C选项进行判断;通过证明△ADE∽△EFC,则利用相似比可对D选项进行判断的.
解:∵DE∥BC,
∴=,所以A选项错误;
∵EF∥AB,
∴=,所以B选项错误;
∵DE∥BC,
∴=,即=,所以C选项错误;
∵DE∥BC,
∴∠AED=∠C,
∵EF∥AB,
∴∠A=∠CEF,
∴△ADE∽△EFC,
∴=,所以D选项正确.
故选:D.
10.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:
①abc<0;
②4a﹣2b+c=0;
③当x>1时,y随x的增大而增大;
④关于x的一元二次方程ax2+bx+c=0有一个实数根.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
解:抛物线开口向上,则a>0,对称轴x=﹣=1,则b=﹣2a<0.与y轴交于负半轴,则c<0,故abc>0,所以①错误;
抛物线对称轴为x=1,与x轴的一个交点为(4,0),则另一个交点为(﹣2,0),于是有4a﹣2b+c=0,所以②正确;
x>1时,y随x的增大而增大,所以③正确;
抛物线与x轴有两个不同交点,因此关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根,所以④错误;
综上所述,正确的结论有:②③,
故选:B.
二.填空题(每题3分,共30分)
11.在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是 (﹣3,﹣2) .
【分析】根据平面直角坐标系内两点关于原点对称横纵坐标互为相反数,即可得出答案.
解:点(3,2)关于原点对称的点的坐标是(﹣3,﹣2),
故答案为:(﹣3,﹣2).
12.抛物线y=2(x+1)2﹣3的顶点坐标为 (﹣1,﹣3). .
【分析】直接利用顶点式的特点可知顶点坐标.
解:顶点坐标是(﹣1,﹣3).
故答案为:(﹣1,﹣3).
13.一辆汽车行驶的路程s(单位:m)关于时间t(单位:s)的函数解析式是s=9t+t2,经过16s汽车行驶了 272 m.
【分析】将t=16代入函数解析式求解即可.
解:当t=16时,s=9×16+×162=272,
∴经过16s汽车行驶了272m,
故答案为:272.
14.反比例函数y=的图象经过点(﹣2,3),则k的值为 ﹣6 .
【分析】将点(﹣2,3)代入解析式可求出k的值.
解:把(﹣2,3)代入函数y=中,得3=,解得k=﹣6.
故答案为:﹣6.
15.如图,AD是△ABC的外接圆⊙O的直径,若∠BAD=40°,则∠ACB= 50 °.
【分析】连接BD,如图,根据圆周角定理即可得到结论.
解:连接BD,如图,
∵AD为△ABC的外接圆⊙O的直径,
∴∠ABD=90°,
∴∠D=90°﹣∠BAD=90°﹣40°=50°,
∴∠ACB=∠D=50°.
故答案为50.
16.在△ABC中,∠C=90°,sinA=,BC=6,则AC的长为 2 .
【分析】根据锐角三角函数的意义,求出AB,再根据勾股定理求出BC即可.
解:∵sinA==,BC=6,
∴AB=8,
∴BC=
=
=
=2,
故答案为:2.
17.若扇形的圆心角为45°,半径为6,则该扇形的弧长为 π .
【分析】把已知数据代入弧长公式,计算即可.
解:由题意,得该扇形的弧长==π,
故答案为:π.
18.AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若△AOM中有一个角是30°,OM=3,则弦AB的长为 6或2 .
【分析】分∠OAM=30°,∠AOM=30°,两种情况分别利用正切的定义求解即可.
解:∵OM⊥AB,
∴AM=BM,
若∠OAM=30°,
则tan∠OAM=,
∴AM=3,
∴AB=2AM=6;
若∠AOM=30°,
则tan∠AOM=,
∴AM=,
∴AB=2AM=2.
故答案为:6或2.
19.同时掷两个质地均匀的骰子,则两个骰子的点数和是10的概率为 .
【分析】列举出所有情况,让两个骰子的点数和是10的情况数除以总情况数即为所求的概率.
解:易得有6×6=36种可能,两个骰子的点数和是10的有4,6;5,5;6,4共3种,所以概率是.
20.如图,△ABC的中线AD与高CE交于点F,AE=EF,FD=2,S△ACF=24,则AB的长为 6 .
【分析】先判断出△BDM≌△CDF进而得出MB=CF,∠M=∠CFD.再判断出△ABM是等腰直角三角形,求得BE=FN=2,然后利用S△ACF=24,即可得出结论.
解:延长AD至点M,使MD=FD,连接MB,
在△BDM和△CDF中,
,
∴△BDM≌△CDF(SAS).
∴MB=CF,∠M=∠CFD.
∴EC∥BM,
∵EA=EF,CE是△ABC的高,
∴∠EAF=∠EFA=45°,
∵EC∥BM,
∴∠ABM=∠AEF=90°,
∴∠M=∠MAB=45°,
∴AB=MB,
∴AB=CF,
∵CE是△ABC的高,S△ACF=24,
∴CF?AE=24,即AB?AE=24,
作FN⊥BM于N,
则四边形EFNB是矩形,△FMN是等腰直角三角形,
∴BE=FN=FM=×2FD=FD=2,
∴AE=AB﹣2,
∴AB?AE=AB(AB﹣2)=24,
∴AB=6(负数舍去),
故答案为6.
三、解答题(60分)
21.先化简,再求代数式(1+)÷值,其中x=3tan30°.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再根据特殊锐角的三角函数值确定x的值,继而代入计算可得答案.
解:原式=(+)÷
=?
=,
当x=3tan30°=3×=时,
原式==.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图中画出等腰△ABC,点C在小正方形顶点上;
(2)在(1)的条件下确定点C后,再确定点D,点D在小正方形顶点上,请你连接DA,DC,DB,使tan∠ACD=,并直接写出四边形ADBC的面积为 4 .
【分析】(1)根据等腰三角形的定义,画出图形即可.
(2)取格点K,连接CK,由tan∠AKC=,证明∠ACD=∠AKC即可.
解:(1)如图,△ABC即为所求作.
(2)如图,四边形ADBC即为所求作.
S四边形ADBC=3×3﹣×1×3﹣×1×1﹣×2×3=4.
故答案为4.
23.为了解疫情期间学生网络学习的学习效果,高远中学随机抽取了部分学生进行调查.要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果.现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题
(1)这次活动共抽查学生多少名?
(2)请通过计算补全条形统计图;
(3)若高远中学共有1600名学生,估计该中学“优秀”等次的学生有多少名?
【分析】(1)通过条形统计图可得“优秀”的有40人,“良好”的有80人,“一般”的有60人,而“良好”的占40%,可求出调查人数;
(2)计算出D等级的人数,即可补全条形统计图;
(3)样本中“优秀”的占调查人数的,因此总体1600人的是“优秀”的人数.
解:(1)80÷40%=200(名),
答:这次活动共抽查学生200名;
(2)200﹣80﹣40﹣60=20(名),
补全条形统计图如图所示:
(3)1600×=320(名),
答:高远中学1600名学生中“优秀”等次的学生大约有320名.
24.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.
(1)求证:CF=AF;
(2)在不添加任何辅助线的情况下,请直接写出图中所有的等腰直角三角形.
【分析】(1)由“SAS”可证△BAD≌△CAE,可得∠ABD=∠ACE=45°,可求∠BCE=90°,由直角三角形斜边上的中线等于斜边的一半证得结论;
(2)根据等腰三角形的判定定理进行推理即可.
【解答】(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE.
在△BAD与△CAE中,
.
∴△BAD≌△CAE(SAS).
∴∠ABD=∠ACE.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°.
∴∠ABD=∠ACE=45°,
∴∠DCE=∠ACB+∠ACE=90°.
∵点F是DE的中点,∠DAE=∠DCE=90°.
∴AF=DE,CF=DE.
∴CF=AF;
(2)解:符合条件的等腰直角三角形有:△ABC,△ADE,△ADF,△AFE.
理由如下:在△ABC中,AB=AC,∠BAC=90°,则△ABC是等腰直角三角形.
在△ADE中,AD=AE,∠DAE=90°,则△DEA是等腰直角三角形.
在等腰Rt△ADE中,∵点F是DE的中点,
∴AD⊥DE,AF=DF=EF=DE,
∴△ADF,△AFE都是等腰直角三角形.
25.某班班主任对在某次考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,若购买甲种笔记本15个,乙种笔记本20个,共花费250元;若购买甲种笔记本10个,乙种笔记本25个,共花费225元.
(1)求购买一个甲种、一个乙种笔记本各需多少元?
(2)班主任决定再次购买甲、乙两种笔记本共35个,如果班主任此次购买甲、乙两种笔记本的总费用不超过300元,求至多需要购买多少个甲种笔记本?
【分析】(1)设购买一个甲种笔记本需x元,一个乙种笔记本需y元,由购买甲种笔记本15个,乙种笔记本20个,共花费250元;若购买甲种笔记本10个,乙种笔记本25个,共花费225元.列出方程组,可求解;
(2)设需要购买a个甲种笔记本,由总费用不超过300元,列出不等式,即可求解.
解:(1)设购买一个甲种笔记本需x元,一个乙种笔记本需y元,
由题意可得:,
解得:,
答:购买一个甲种笔记本需10元,一个乙种笔记本需5元;
(2)设需要购买a个甲种笔记本,
由题意可得:10a+5(35﹣a)≤300,
解得:a≤25,
答:至多需要购买25个甲种笔记本.
26.△ABC内接于⊙O,CA=CB,BD为⊙O的直径,∠DBC=30°.
(1)如图1,求证:△ABC为等边三角形;
(2)如图2,弦AE交BC于点F,点G在EC上,∠BAF=∠GAF,求证:FB=FG;
(3)如图3,在(2)的条件下,弦BH分别交AF,AG于P,Q两点,PO=DH=,AC=3,求QG的长.
【分析】(1)如图1,连接CD,由∠BAC=60°、CA=CB证得△ABC为等边三角形;
(2)如图2,根据△BAF≌△GAF(SAS)的对应边相等证得FB=FG;
(3)如图3,过点O作OL⊥PH,点L为垂足.
首先,推知Rt△POL中的∠OPL=30°;连接AH,延长PO交AH于点M,构造等边△AHP;
然后,连接AD,通过解直角△ABD得到BD=2,在直角△BDH中,利用勾股定理求得BH=9,继而根据垂径定理推知BL=LH=,所以通过解直角△POL求得PL=.由图中线段间的和差关系易得PH=6,BP=3.则等边三角形△AHP中,得到,AP=PH=6,∠APH=60°;
最后,连接BE,构造等边△BPE,根据等边三角形的性质和平行线的判定定理推知PQ∥EG,结合平行线截线段成比例求得QG=.
【解答】(1)证明:如图1,连接CD,
∵BD为⊙O的直径,
∴∠BCD=90°.
∵∠DBC=30°,
∴∠BDC=90°﹣∠DBC=60°.
∴∠BAC=∠BDC=60°.
∵CA=CB,
∴△ABC为等边三角形;
(2)证明:如图2,
∵△ABC为等边三角形,
∴∠ABC=∠ACB.
∵∠E=∠ABC,
∴∠ACB=∠E.
∵∠BAF=∠GAF,∠BAF=∠BCE,
∴∠GAF=∠BCE.
∴∠ACB+∠BCE=∠E+∠GAF.
∵∠AGC=∠E+∠GAF,
∴∠AGC=∠ACG.
∴AG=AC.
∵△ABC为等边三角形,
∴AC=AB.
∴AB=AG.
∵∠BAF=GAF,AE=AF,
∴△BAF≌△GAF(SAS).
∴FB=FG;
(3)解:如图3,过点O作OL⊥PH,点L为垂足.
∵点O为圆心,
∴BL=LH,
∵BO=OD,
∴OL=DH.
∵PO=DH,
∴OL=PO.
在Rt△POL中,sin∠OPL==.
∴∠OPL=30°.
连接AH,延长PO交AH于点M,
∵△ABC是等边三角形,
∴∠ACB=60°.
∴∠AHB=∠ACB=60°.
∴∠PMH=180°﹣∠AHB﹣∠OPL=90°.
∴OM⊥AH.
∴AM=MH.
∴PA=PH.
∵∠AHP=60°.
∴△AHP是等边三角形.
连接AD,
∵BD为⊙O的直径,
∴∠BAD=90°.
∵△ABC是等边三角形,
∴AB=AC=3.
∵∠ADB=∠ACB=60°.
∴在直角△ABD内,sin∠ADB=,BD==2.
∵BD为⊙O的直径,
∴∠BHD=90°.
在直角△BDH中,BD2=BH2+DH2,
∴BH=9.
∵OL⊥PH,
∴BL=LH=.
在直角△POL中,cos∠OPL==.
∵∠OPL=30°.
∴PL==.
∴PH=6,BP=3.
∵△AHP是等边三角形,
∴AP=PH=6,∠APH=60°.
连接BE,
∵∠BEA=∠ACB=60°,∠BPE=∠APH=60°,
∴∠PBE=60°.
∴∠PBE=∠BPE=∠BEA.
∴△BPE是等边三角形.
∴PE=PB=3.
∴AE=9.
∵∠AEC=∠ABC=∠BPE=60°,
∴PQ∥EG.
∴=.
∵AG=AC=3.
∴QG=.
27.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx﹣3交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C,OB=OC=OA.
(1)如图1,求抛物线的解析式;
(2)如图2,点D在抛物线上,且点D在第二象限,连接BD交y轴于点E,若tan∠EBA=,求点D的坐标;
(3)如图3,在(2)的条件下,点P在抛物线上,且点P在第三象限,点F在PB上,FC=FB,过点F作x轴的垂线,点G为垂足,连接DG并延长交BF于点H,若∠DHP=∠CEB,求BP的长.
【分析】(1)利用二次函数图象上点的坐标可求出点C的坐标,进而可得出OC的长,结合OB=OC=3/2OA,可求出OB,OA的长,进而可得出点A,B的坐标,再利用待定系数法即可求出二次函数解析式;
(2)在Rt△OBE中,通过解直角三角形可求出OE的长,进而可得出点E的坐标,根据点B,E的坐标,利用待定系数法可求出直线BE的解析式,再联立两函数解析式成方程组,解之即可得出点D的坐标(舍去点B的坐标);
(3)连接OF,过点F作y轴的垂线,点T为垂足,取OM的中点N,连接DN,过点G作DN的垂线交DN的延长线于点R,依次证明△OFB≌△OFC(SSS)、四边形OTFG为正方形、△OEB≌△MND(SAS);设OG=GF=m,BG=3﹣m,NG=+m,由tan∠NDG=tan∠GBF,得关于m的等式,解得m的值;设点P的横坐标为n,则点P的纵坐标为﹣﹣3,在Rt△PWB中,由tan∠PBW==,得关于n的方程,解得n的值;最后在Rt△PWB中,根据BP2=PW2+BW2,求得BP的长即可.
解:(1)∵二次函数y=ax2+bx﹣3,
∴当x=0时,y=3,C(0,﹣3),
∴OC=3,
∵OB=OC=OA,OB=3,OA=2,
∴B (3,0),A(﹣2,0),
∴,
解得,
∴抛物线的解析式为y=;
(2)过点D作x轴的垂线,点M为垂足,设点D的横坐标为t,则点D的纵坐标为,
∵点D在第二象限,
∴DM=,
∵OM=﹣t,OB=3,
∴MB=﹣t+3,
在Rt△DMB中,tan∠DBA=,
∵tan∠EBA=,
∴2DM=MB,2()=﹣t+3,
解得t1=3(舍去),t2=﹣3,
∴点D的纵坐标为﹣3=3,
∴点D的坐标为(﹣3,3);
(3)连接OF,
∵OB=OC,FB=FC,OF=OF,
∴△OFB≌△OFC(SSS),
∴∠COF=∠BOF;
过点F作y轴的垂线,点T为垂足,
∵FG⊥OB,
∴FT=FG,
∵∠BOT=∠OTF=∠FGO=90°,
∴四边形OTFG为矩形;
∵FT=FG,
∴四边形OTFG为正方形;
取OM的中点N,连接DN,过点G作DN的垂线交DN的延长线于点R,
在Rt△OEB中,tan∠EBO==,
∴OE=;
∵OM=3,
∴MN=,
∴MN=OE;
∵DM=OB=3;
∴∠DMN=∠EOB=90°,
∴△OEB≌△MND(SAS),
∴∠DNM=∠OEB,
∵∠DHP=∠CEB,
∴∠DNM=∠DHP,
∵∠DNM=∠DGN+∠NDG,∠DHP=∠HGB+∠GBF,∠DGN=∠HGB,
∴∠NDG=∠GBF;
在Rt△OEB中,OE=,BO=3,BE2=OB2+OE2,
∴BE=,
∴DN=,
在Rt△DNM中,tan∠DNM==2,∠DNM=∠GNR,
在Rt△GNR中,tan∠GNR==2,
∴RG=2RN;
在Rt△GNR中,NR2+RG2=NR2,
∴NR=5NG,
∵四边形OTFG为正方形,
∴设OG=GF=m,BG=3﹣m,NG=+m,
NR=(+m),RG=(+m),
∵∠NDG=∠GBF,
∴tan∠NDG=tan∠GBF,
在Rt△DGR中 tan∠RDG=,
在Rt△GBF中 tan∠GBF=,
∴=,
解得m1=﹣3(舍去),m2=1;
∴tan∠GBF=.
过点P作x轴的垂线,点W为垂足,
设点P的横坐标为n,则点P的纵坐标为﹣﹣3,
∵点P在第三象限,
∴PW=﹣++3,
在Rt△PWB中,tan∠PBW==,
∴2PW=BW,
∵OW=﹣n.
∴BW=﹣n+3,
∴2(﹣++3)=﹣n+3,
解得n1=3(舍去),n2=﹣1,
∴BW=4,PW=2.
在Rt△PWB中,BP2=PW2+BW2,
∴BP=2.
一.选择题(共10小题).
1.下列各点中,在反比例函数y=图象上的是( )
A.(﹣1,8) B.(﹣2,4) C.(1,7) D.(2,4)
2.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
3.袋子中装有4个黑球、2个白球,这些球的形状、大小、质地完全相同,即除颜色外无其他差别.在看不到球的条件下,随机从袋中摸出1个球,是白球的概率是( )
A. B. C. D.
4.下面四个几何体中,主视图为三角形的是( )
A. B.
C. D.
5.把函数y=(x﹣1)2+2图象向右平移1个单位长度,平移后图象的函数解析式为( )
A.y=x2+2 B.y=(x﹣1)2+1 C.y=(x﹣2)2+2 D.y=(x﹣1)2﹣3
6.如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
A.(1.5+150tanα)米 B.(1.5+)米
C.(1.5+150sinα)米 D.(1.5+)米
7.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长度是( )
A.1cm B.2cm C.cm D.2cm
8.如图,⊙O为△ABC的外接圆,已知∠ABC为130°,则∠AOC的度数为( )
A.50° B.80° C.100° D.115°
9.如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,则下列式子一定正确的是( )
A. B. C. D.
10.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:
①abc<0;
②4a﹣2b+c=0;
③当x>1时,y随x的增大而增大;
④关于x的一元二次方程ax2+bx+c=0有一个实数根.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共10小题).
11.在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是 .
12.抛物线y=2(x+1)2﹣3的顶点坐标为 .
13.一辆汽车行驶的路程s(单位:m)关于时间t(单位:s)的函数解析式是s=9t+t2,经过16s汽车行驶了 m.
14.反比例函数y=的图象经过点(﹣2,3),则k的值为 .
15.如图,AD是△ABC的外接圆⊙O的直径,若∠BAD=40°,则∠ACB= °.
16.在△ABC中,∠C=90°,sinA=,BC=6,则AC的长为 .
17.若扇形的圆心角为45°,半径为6,则该扇形的弧长为 .
18.AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若△AOM中有一个角是30°,OM=3,则弦AB的长为 .
19.同时掷两个质地均匀的骰子,则两个骰子的点数和是10的概率为 .
20.如图,△ABC的中线AD与高CE交于点F,AE=EF,FD=2,S△ACF=24,则AB的长为 .
三、解答题(60分)
21.先化简,再求代数式(1+)÷值,其中x=3tan30°.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图中画出等腰△ABC,点C在小正方形顶点上;
(2)在(1)的条件下确定点C后,再确定点D,点D在小正方形顶点上,请你连接DA,DC,DB,使tan∠ACD=,并直接写出四边形ADBC的面积为 .
23.为了解疫情期间学生网络学习的学习效果,高远中学随机抽取了部分学生进行调查.要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果.现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题
(1)这次活动共抽查学生多少名?
(2)请通过计算补全条形统计图;
(3)若高远中学共有1600名学生,估计该中学“优秀”等次的学生有多少名?
24.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.
(1)求证:CF=AF;
(2)在不添加任何辅助线的情况下,请直接写出图中所有的等腰直角三角形.
25.某班班主任对在某次考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,若购买甲种笔记本15个,乙种笔记本20个,共花费250元;若购买甲种笔记本10个,乙种笔记本25个,共花费225元.
(1)求购买一个甲种、一个乙种笔记本各需多少元?
(2)班主任决定再次购买甲、乙两种笔记本共35个,如果班主任此次购买甲、乙两种笔记本的总费用不超过300元,求至多需要购买多少个甲种笔记本?
26.△ABC内接于⊙O,CA=CB,BD为⊙O的直径,∠DBC=30°.
(1)如图1,求证:△ABC为等边三角形;
(2)如图2,弦AE交BC于点F,点G在EC上,∠BAF=∠GAF,求证:FB=FG;
(3)如图3,在(2)的条件下,弦BH分别交AF,AG于P,Q两点,PO=DH=,AC=3,求QG的长.
27.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx﹣3交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C,OB=OC=OA.
(1)如图1,求抛物线的解析式;
(2)如图2,点D在抛物线上,且点D在第二象限,连接BD交y轴于点E,若tan∠EBA=,求点D的坐标;
(3)如图3,在(2)的条件下,点P在抛物线上,且点P在第三象限,点F在PB上,FC=FB,过点F作x轴的垂线,点G为垂足,连接DG并延长交BF于点H,若∠DHP=∠CEB,求BP的长.
参考答案
一.选择题(共10小题).
1.下列各点中,在反比例函数y=图象上的是( )
A.(﹣1,8) B.(﹣2,4) C.(1,7) D.(2,4)
解:A、∵﹣1×8=﹣8≠8,∴该点不在函数图象上,故本选项错不合题意;
B、∵﹣2×4=﹣8≠8,∴该点不在函数图象上,故本选项不合题意;
C、∵1×7=7≠8,∴该点不在函数图象上,故本选项不合题意;
D、2×4=8,∴该点在函数图象上,故本选项符合题意.
故选:D.
2.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.
解:A、既不是轴对称图形,也不是中心对称图形,故本选项不合题意;
B、不是轴对称图形,是中心对称图形,故本选项不合题意;
C、是轴对称图形,不是中心对称图形,故本选项不合题意;
D、既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
3.袋子中装有4个黑球、2个白球,这些球的形状、大小、质地完全相同,即除颜色外无其他差别.在看不到球的条件下,随机从袋中摸出1个球,是白球的概率是( )
A. B. C. D.
【分析】用白球的个数除以总球的个数即可得出答案.
解:∵袋子中装有4个黑球、2个白球,共有6个球,
∴随机从袋中摸出1个球,是白球的概率是=.
故选:A.
4.下面四个几何体中,主视图为三角形的是( )
A. B.
C. D.
【分析】根据主视图是从正面看得到的图形,可得答案.
解:A、主视图是圆,故A不符合题意;
B、主视图是三角形,故B符合题意;
C、主视图是矩形,故C不符合题意;
D、主视图是正方形,故D不符合题意;
故选:B.
5.把函数y=(x﹣1)2+2图象向右平移1个单位长度,平移后图象的函数解析式为( )
A.y=x2+2 B.y=(x﹣1)2+1 C.y=(x﹣2)2+2 D.y=(x﹣1)2﹣3
解:二次函数y=(x﹣1)2+2的图象的顶点坐标为(1,2),
∴向右平移1个单位长度后的函数图象的顶点坐标为(2,2),
∴所得的图象解析式为y=(x﹣2)2+2.
故选:C.
6.如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
A.(1.5+150tanα)米 B.(1.5+)米
C.(1.5+150sinα)米 D.(1.5+)米
【分析】过点A作AE⊥BC,E为垂足,再由锐角三角函数的定义求出BE的长,由BC=CE+BE即可得出结论.
解:过点A作AE⊥BC,E为垂足,如图所示:
则四边形ADCE为矩形,AE=150,
∴CE=AD=1.5,
在△ABE中,∵tanα==,
∴BE=150tanα,
∴BC=CE+BE=(1.5+150tanα)(m),
故选:A.
7.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长度是( )
A.1cm B.2cm C.cm D.2cm
【分析】由直角三角形的性质得到AB=2AC=2,然后根据旋转的性质和线段垂直平分线的性质得到AB′=BB′.
解:∵在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1cm,
∴AC=AB,则AB=2AC=2cm.
又由旋转的性质知,AC′=AC=AB,B′C′⊥AB,
∴B′C′是△ABB′的中垂线,
∴AB′=BB′.
根据旋转的性质知AB=AB′=BB′=2cm.
故选:B.
8.如图,⊙O为△ABC的外接圆,已知∠ABC为130°,则∠AOC的度数为( )
A.50° B.80° C.100° D.115°
解:作所对的圆周角∠ADC,如图,
∵∠ADC+∠ABC=180°,
而∠ABC=130°,
∴∠ADC=180°﹣130°=50°,
∴∠AOC=2∠ADC=100°.
故选:C.
9.如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,则下列式子一定正确的是( )
A. B. C. D.
【分析】根据平行线分线段成比例可对A选项和B选项进行判断;:利用DE∥BC得到=,则根据比例的性质可对C选项进行判断;通过证明△ADE∽△EFC,则利用相似比可对D选项进行判断的.
解:∵DE∥BC,
∴=,所以A选项错误;
∵EF∥AB,
∴=,所以B选项错误;
∵DE∥BC,
∴=,即=,所以C选项错误;
∵DE∥BC,
∴∠AED=∠C,
∵EF∥AB,
∴∠A=∠CEF,
∴△ADE∽△EFC,
∴=,所以D选项正确.
故选:D.
10.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:
①abc<0;
②4a﹣2b+c=0;
③当x>1时,y随x的增大而增大;
④关于x的一元二次方程ax2+bx+c=0有一个实数根.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
解:抛物线开口向上,则a>0,对称轴x=﹣=1,则b=﹣2a<0.与y轴交于负半轴,则c<0,故abc>0,所以①错误;
抛物线对称轴为x=1,与x轴的一个交点为(4,0),则另一个交点为(﹣2,0),于是有4a﹣2b+c=0,所以②正确;
x>1时,y随x的增大而增大,所以③正确;
抛物线与x轴有两个不同交点,因此关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根,所以④错误;
综上所述,正确的结论有:②③,
故选:B.
二.填空题(每题3分,共30分)
11.在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是 (﹣3,﹣2) .
【分析】根据平面直角坐标系内两点关于原点对称横纵坐标互为相反数,即可得出答案.
解:点(3,2)关于原点对称的点的坐标是(﹣3,﹣2),
故答案为:(﹣3,﹣2).
12.抛物线y=2(x+1)2﹣3的顶点坐标为 (﹣1,﹣3). .
【分析】直接利用顶点式的特点可知顶点坐标.
解:顶点坐标是(﹣1,﹣3).
故答案为:(﹣1,﹣3).
13.一辆汽车行驶的路程s(单位:m)关于时间t(单位:s)的函数解析式是s=9t+t2,经过16s汽车行驶了 272 m.
【分析】将t=16代入函数解析式求解即可.
解:当t=16时,s=9×16+×162=272,
∴经过16s汽车行驶了272m,
故答案为:272.
14.反比例函数y=的图象经过点(﹣2,3),则k的值为 ﹣6 .
【分析】将点(﹣2,3)代入解析式可求出k的值.
解:把(﹣2,3)代入函数y=中,得3=,解得k=﹣6.
故答案为:﹣6.
15.如图,AD是△ABC的外接圆⊙O的直径,若∠BAD=40°,则∠ACB= 50 °.
【分析】连接BD,如图,根据圆周角定理即可得到结论.
解:连接BD,如图,
∵AD为△ABC的外接圆⊙O的直径,
∴∠ABD=90°,
∴∠D=90°﹣∠BAD=90°﹣40°=50°,
∴∠ACB=∠D=50°.
故答案为50.
16.在△ABC中,∠C=90°,sinA=,BC=6,则AC的长为 2 .
【分析】根据锐角三角函数的意义,求出AB,再根据勾股定理求出BC即可.
解:∵sinA==,BC=6,
∴AB=8,
∴BC=
=
=
=2,
故答案为:2.
17.若扇形的圆心角为45°,半径为6,则该扇形的弧长为 π .
【分析】把已知数据代入弧长公式,计算即可.
解:由题意,得该扇形的弧长==π,
故答案为:π.
18.AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若△AOM中有一个角是30°,OM=3,则弦AB的长为 6或2 .
【分析】分∠OAM=30°,∠AOM=30°,两种情况分别利用正切的定义求解即可.
解:∵OM⊥AB,
∴AM=BM,
若∠OAM=30°,
则tan∠OAM=,
∴AM=3,
∴AB=2AM=6;
若∠AOM=30°,
则tan∠AOM=,
∴AM=,
∴AB=2AM=2.
故答案为:6或2.
19.同时掷两个质地均匀的骰子,则两个骰子的点数和是10的概率为 .
【分析】列举出所有情况,让两个骰子的点数和是10的情况数除以总情况数即为所求的概率.
解:易得有6×6=36种可能,两个骰子的点数和是10的有4,6;5,5;6,4共3种,所以概率是.
20.如图,△ABC的中线AD与高CE交于点F,AE=EF,FD=2,S△ACF=24,则AB的长为 6 .
【分析】先判断出△BDM≌△CDF进而得出MB=CF,∠M=∠CFD.再判断出△ABM是等腰直角三角形,求得BE=FN=2,然后利用S△ACF=24,即可得出结论.
解:延长AD至点M,使MD=FD,连接MB,
在△BDM和△CDF中,
,
∴△BDM≌△CDF(SAS).
∴MB=CF,∠M=∠CFD.
∴EC∥BM,
∵EA=EF,CE是△ABC的高,
∴∠EAF=∠EFA=45°,
∵EC∥BM,
∴∠ABM=∠AEF=90°,
∴∠M=∠MAB=45°,
∴AB=MB,
∴AB=CF,
∵CE是△ABC的高,S△ACF=24,
∴CF?AE=24,即AB?AE=24,
作FN⊥BM于N,
则四边形EFNB是矩形,△FMN是等腰直角三角形,
∴BE=FN=FM=×2FD=FD=2,
∴AE=AB﹣2,
∴AB?AE=AB(AB﹣2)=24,
∴AB=6(负数舍去),
故答案为6.
三、解答题(60分)
21.先化简,再求代数式(1+)÷值,其中x=3tan30°.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再根据特殊锐角的三角函数值确定x的值,继而代入计算可得答案.
解:原式=(+)÷
=?
=,
当x=3tan30°=3×=时,
原式==.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图中画出等腰△ABC,点C在小正方形顶点上;
(2)在(1)的条件下确定点C后,再确定点D,点D在小正方形顶点上,请你连接DA,DC,DB,使tan∠ACD=,并直接写出四边形ADBC的面积为 4 .
【分析】(1)根据等腰三角形的定义,画出图形即可.
(2)取格点K,连接CK,由tan∠AKC=,证明∠ACD=∠AKC即可.
解:(1)如图,△ABC即为所求作.
(2)如图,四边形ADBC即为所求作.
S四边形ADBC=3×3﹣×1×3﹣×1×1﹣×2×3=4.
故答案为4.
23.为了解疫情期间学生网络学习的学习效果,高远中学随机抽取了部分学生进行调查.要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果.现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题
(1)这次活动共抽查学生多少名?
(2)请通过计算补全条形统计图;
(3)若高远中学共有1600名学生,估计该中学“优秀”等次的学生有多少名?
【分析】(1)通过条形统计图可得“优秀”的有40人,“良好”的有80人,“一般”的有60人,而“良好”的占40%,可求出调查人数;
(2)计算出D等级的人数,即可补全条形统计图;
(3)样本中“优秀”的占调查人数的,因此总体1600人的是“优秀”的人数.
解:(1)80÷40%=200(名),
答:这次活动共抽查学生200名;
(2)200﹣80﹣40﹣60=20(名),
补全条形统计图如图所示:
(3)1600×=320(名),
答:高远中学1600名学生中“优秀”等次的学生大约有320名.
24.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.
(1)求证:CF=AF;
(2)在不添加任何辅助线的情况下,请直接写出图中所有的等腰直角三角形.
【分析】(1)由“SAS”可证△BAD≌△CAE,可得∠ABD=∠ACE=45°,可求∠BCE=90°,由直角三角形斜边上的中线等于斜边的一半证得结论;
(2)根据等腰三角形的判定定理进行推理即可.
【解答】(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE.
在△BAD与△CAE中,
.
∴△BAD≌△CAE(SAS).
∴∠ABD=∠ACE.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°.
∴∠ABD=∠ACE=45°,
∴∠DCE=∠ACB+∠ACE=90°.
∵点F是DE的中点,∠DAE=∠DCE=90°.
∴AF=DE,CF=DE.
∴CF=AF;
(2)解:符合条件的等腰直角三角形有:△ABC,△ADE,△ADF,△AFE.
理由如下:在△ABC中,AB=AC,∠BAC=90°,则△ABC是等腰直角三角形.
在△ADE中,AD=AE,∠DAE=90°,则△DEA是等腰直角三角形.
在等腰Rt△ADE中,∵点F是DE的中点,
∴AD⊥DE,AF=DF=EF=DE,
∴△ADF,△AFE都是等腰直角三角形.
25.某班班主任对在某次考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,若购买甲种笔记本15个,乙种笔记本20个,共花费250元;若购买甲种笔记本10个,乙种笔记本25个,共花费225元.
(1)求购买一个甲种、一个乙种笔记本各需多少元?
(2)班主任决定再次购买甲、乙两种笔记本共35个,如果班主任此次购买甲、乙两种笔记本的总费用不超过300元,求至多需要购买多少个甲种笔记本?
【分析】(1)设购买一个甲种笔记本需x元,一个乙种笔记本需y元,由购买甲种笔记本15个,乙种笔记本20个,共花费250元;若购买甲种笔记本10个,乙种笔记本25个,共花费225元.列出方程组,可求解;
(2)设需要购买a个甲种笔记本,由总费用不超过300元,列出不等式,即可求解.
解:(1)设购买一个甲种笔记本需x元,一个乙种笔记本需y元,
由题意可得:,
解得:,
答:购买一个甲种笔记本需10元,一个乙种笔记本需5元;
(2)设需要购买a个甲种笔记本,
由题意可得:10a+5(35﹣a)≤300,
解得:a≤25,
答:至多需要购买25个甲种笔记本.
26.△ABC内接于⊙O,CA=CB,BD为⊙O的直径,∠DBC=30°.
(1)如图1,求证:△ABC为等边三角形;
(2)如图2,弦AE交BC于点F,点G在EC上,∠BAF=∠GAF,求证:FB=FG;
(3)如图3,在(2)的条件下,弦BH分别交AF,AG于P,Q两点,PO=DH=,AC=3,求QG的长.
【分析】(1)如图1,连接CD,由∠BAC=60°、CA=CB证得△ABC为等边三角形;
(2)如图2,根据△BAF≌△GAF(SAS)的对应边相等证得FB=FG;
(3)如图3,过点O作OL⊥PH,点L为垂足.
首先,推知Rt△POL中的∠OPL=30°;连接AH,延长PO交AH于点M,构造等边△AHP;
然后,连接AD,通过解直角△ABD得到BD=2,在直角△BDH中,利用勾股定理求得BH=9,继而根据垂径定理推知BL=LH=,所以通过解直角△POL求得PL=.由图中线段间的和差关系易得PH=6,BP=3.则等边三角形△AHP中,得到,AP=PH=6,∠APH=60°;
最后,连接BE,构造等边△BPE,根据等边三角形的性质和平行线的判定定理推知PQ∥EG,结合平行线截线段成比例求得QG=.
【解答】(1)证明:如图1,连接CD,
∵BD为⊙O的直径,
∴∠BCD=90°.
∵∠DBC=30°,
∴∠BDC=90°﹣∠DBC=60°.
∴∠BAC=∠BDC=60°.
∵CA=CB,
∴△ABC为等边三角形;
(2)证明:如图2,
∵△ABC为等边三角形,
∴∠ABC=∠ACB.
∵∠E=∠ABC,
∴∠ACB=∠E.
∵∠BAF=∠GAF,∠BAF=∠BCE,
∴∠GAF=∠BCE.
∴∠ACB+∠BCE=∠E+∠GAF.
∵∠AGC=∠E+∠GAF,
∴∠AGC=∠ACG.
∴AG=AC.
∵△ABC为等边三角形,
∴AC=AB.
∴AB=AG.
∵∠BAF=GAF,AE=AF,
∴△BAF≌△GAF(SAS).
∴FB=FG;
(3)解:如图3,过点O作OL⊥PH,点L为垂足.
∵点O为圆心,
∴BL=LH,
∵BO=OD,
∴OL=DH.
∵PO=DH,
∴OL=PO.
在Rt△POL中,sin∠OPL==.
∴∠OPL=30°.
连接AH,延长PO交AH于点M,
∵△ABC是等边三角形,
∴∠ACB=60°.
∴∠AHB=∠ACB=60°.
∴∠PMH=180°﹣∠AHB﹣∠OPL=90°.
∴OM⊥AH.
∴AM=MH.
∴PA=PH.
∵∠AHP=60°.
∴△AHP是等边三角形.
连接AD,
∵BD为⊙O的直径,
∴∠BAD=90°.
∵△ABC是等边三角形,
∴AB=AC=3.
∵∠ADB=∠ACB=60°.
∴在直角△ABD内,sin∠ADB=,BD==2.
∵BD为⊙O的直径,
∴∠BHD=90°.
在直角△BDH中,BD2=BH2+DH2,
∴BH=9.
∵OL⊥PH,
∴BL=LH=.
在直角△POL中,cos∠OPL==.
∵∠OPL=30°.
∴PL==.
∴PH=6,BP=3.
∵△AHP是等边三角形,
∴AP=PH=6,∠APH=60°.
连接BE,
∵∠BEA=∠ACB=60°,∠BPE=∠APH=60°,
∴∠PBE=60°.
∴∠PBE=∠BPE=∠BEA.
∴△BPE是等边三角形.
∴PE=PB=3.
∴AE=9.
∵∠AEC=∠ABC=∠BPE=60°,
∴PQ∥EG.
∴=.
∵AG=AC=3.
∴QG=.
27.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx﹣3交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C,OB=OC=OA.
(1)如图1,求抛物线的解析式;
(2)如图2,点D在抛物线上,且点D在第二象限,连接BD交y轴于点E,若tan∠EBA=,求点D的坐标;
(3)如图3,在(2)的条件下,点P在抛物线上,且点P在第三象限,点F在PB上,FC=FB,过点F作x轴的垂线,点G为垂足,连接DG并延长交BF于点H,若∠DHP=∠CEB,求BP的长.
【分析】(1)利用二次函数图象上点的坐标可求出点C的坐标,进而可得出OC的长,结合OB=OC=3/2OA,可求出OB,OA的长,进而可得出点A,B的坐标,再利用待定系数法即可求出二次函数解析式;
(2)在Rt△OBE中,通过解直角三角形可求出OE的长,进而可得出点E的坐标,根据点B,E的坐标,利用待定系数法可求出直线BE的解析式,再联立两函数解析式成方程组,解之即可得出点D的坐标(舍去点B的坐标);
(3)连接OF,过点F作y轴的垂线,点T为垂足,取OM的中点N,连接DN,过点G作DN的垂线交DN的延长线于点R,依次证明△OFB≌△OFC(SSS)、四边形OTFG为正方形、△OEB≌△MND(SAS);设OG=GF=m,BG=3﹣m,NG=+m,由tan∠NDG=tan∠GBF,得关于m的等式,解得m的值;设点P的横坐标为n,则点P的纵坐标为﹣﹣3,在Rt△PWB中,由tan∠PBW==,得关于n的方程,解得n的值;最后在Rt△PWB中,根据BP2=PW2+BW2,求得BP的长即可.
解:(1)∵二次函数y=ax2+bx﹣3,
∴当x=0时,y=3,C(0,﹣3),
∴OC=3,
∵OB=OC=OA,OB=3,OA=2,
∴B (3,0),A(﹣2,0),
∴,
解得,
∴抛物线的解析式为y=;
(2)过点D作x轴的垂线,点M为垂足,设点D的横坐标为t,则点D的纵坐标为,
∵点D在第二象限,
∴DM=,
∵OM=﹣t,OB=3,
∴MB=﹣t+3,
在Rt△DMB中,tan∠DBA=,
∵tan∠EBA=,
∴2DM=MB,2()=﹣t+3,
解得t1=3(舍去),t2=﹣3,
∴点D的纵坐标为﹣3=3,
∴点D的坐标为(﹣3,3);
(3)连接OF,
∵OB=OC,FB=FC,OF=OF,
∴△OFB≌△OFC(SSS),
∴∠COF=∠BOF;
过点F作y轴的垂线,点T为垂足,
∵FG⊥OB,
∴FT=FG,
∵∠BOT=∠OTF=∠FGO=90°,
∴四边形OTFG为矩形;
∵FT=FG,
∴四边形OTFG为正方形;
取OM的中点N,连接DN,过点G作DN的垂线交DN的延长线于点R,
在Rt△OEB中,tan∠EBO==,
∴OE=;
∵OM=3,
∴MN=,
∴MN=OE;
∵DM=OB=3;
∴∠DMN=∠EOB=90°,
∴△OEB≌△MND(SAS),
∴∠DNM=∠OEB,
∵∠DHP=∠CEB,
∴∠DNM=∠DHP,
∵∠DNM=∠DGN+∠NDG,∠DHP=∠HGB+∠GBF,∠DGN=∠HGB,
∴∠NDG=∠GBF;
在Rt△OEB中,OE=,BO=3,BE2=OB2+OE2,
∴BE=,
∴DN=,
在Rt△DNM中,tan∠DNM==2,∠DNM=∠GNR,
在Rt△GNR中,tan∠GNR==2,
∴RG=2RN;
在Rt△GNR中,NR2+RG2=NR2,
∴NR=5NG,
∵四边形OTFG为正方形,
∴设OG=GF=m,BG=3﹣m,NG=+m,
NR=(+m),RG=(+m),
∵∠NDG=∠GBF,
∴tan∠NDG=tan∠GBF,
在Rt△DGR中 tan∠RDG=,
在Rt△GBF中 tan∠GBF=,
∴=,
解得m1=﹣3(舍去),m2=1;
∴tan∠GBF=.
过点P作x轴的垂线,点W为垂足,
设点P的横坐标为n,则点P的纵坐标为﹣﹣3,
∵点P在第三象限,
∴PW=﹣++3,
在Rt△PWB中,tan∠PBW==,
∴2PW=BW,
∵OW=﹣n.
∴BW=﹣n+3,
∴2(﹣++3)=﹣n+3,
解得n1=3(舍去),n2=﹣1,
∴BW=4,PW=2.
在Rt△PWB中,BP2=PW2+BW2,
∴BP=2.
同课章节目录
