2020-2021学年山东省泰安市东平县九年级(上)期末数学试卷(五四学制) (Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省泰安市东平县九年级(上)期末数学试卷(五四学制) (Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 949.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 00:00:00 | ||
图片预览


文档简介
2020-2021学年山东省泰安市东平县九年级第一学期期末数学试卷(五四学制)
一、选择题(共12小题).
1.若点A(3,﹣4)、B(﹣2,m)在同一个反比例函数的图象上,则m的值为( )
A.6 B.﹣6 C.12 D.﹣12
2.圆形的物体在太阳光的投影下是( )
A.圆形 B.椭圆形
C.线段 D.以上都有可能
3.袋中有5个白球,有n个红球,从中任意取一个,恰为红球的机会是,则n为( )
A.16 B.10 C.20 D.18
4.若点A(﹣2,y1),B(﹣1,y2),C(1,y3)在反比例函数y=﹣的图象上,则下列结论正确的是( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y2>y3>y1
5.小明沿着坡度为1:2的山坡向下走了1000m,则他下降了( )
A.200m B.500m C.500m D.1000m
6.用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( )
A.2πcm B.1.5cm C.πcm D.1cm
7.在 Rt△ABC中,∠C=90°,cosB=,则tanA的值为( )
A. B. C. D.
8.如图摆放的几何体的左视图是( )
A. B. C. D.
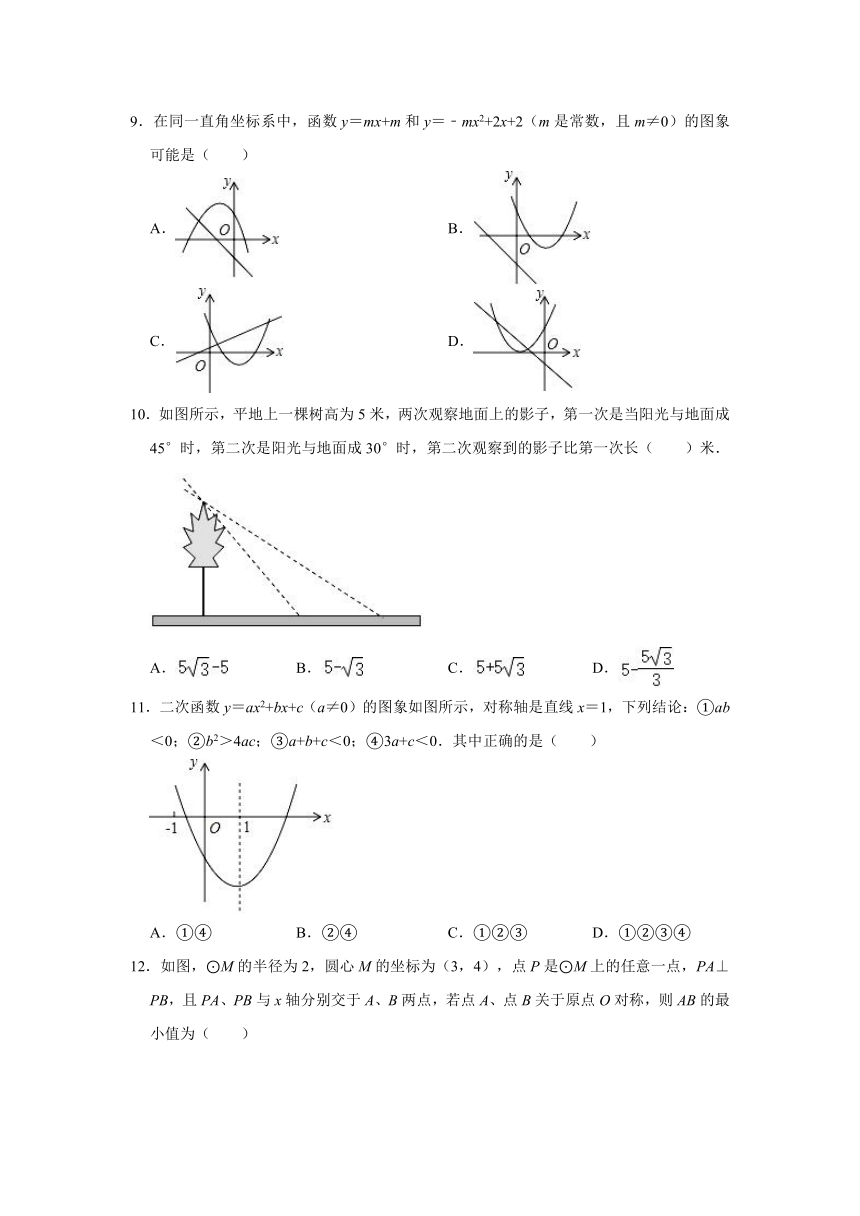
9.在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. B.
C. D.
10.如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长( )米.
A. B. C. D.
11.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+c<0;④3a+c<0.其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
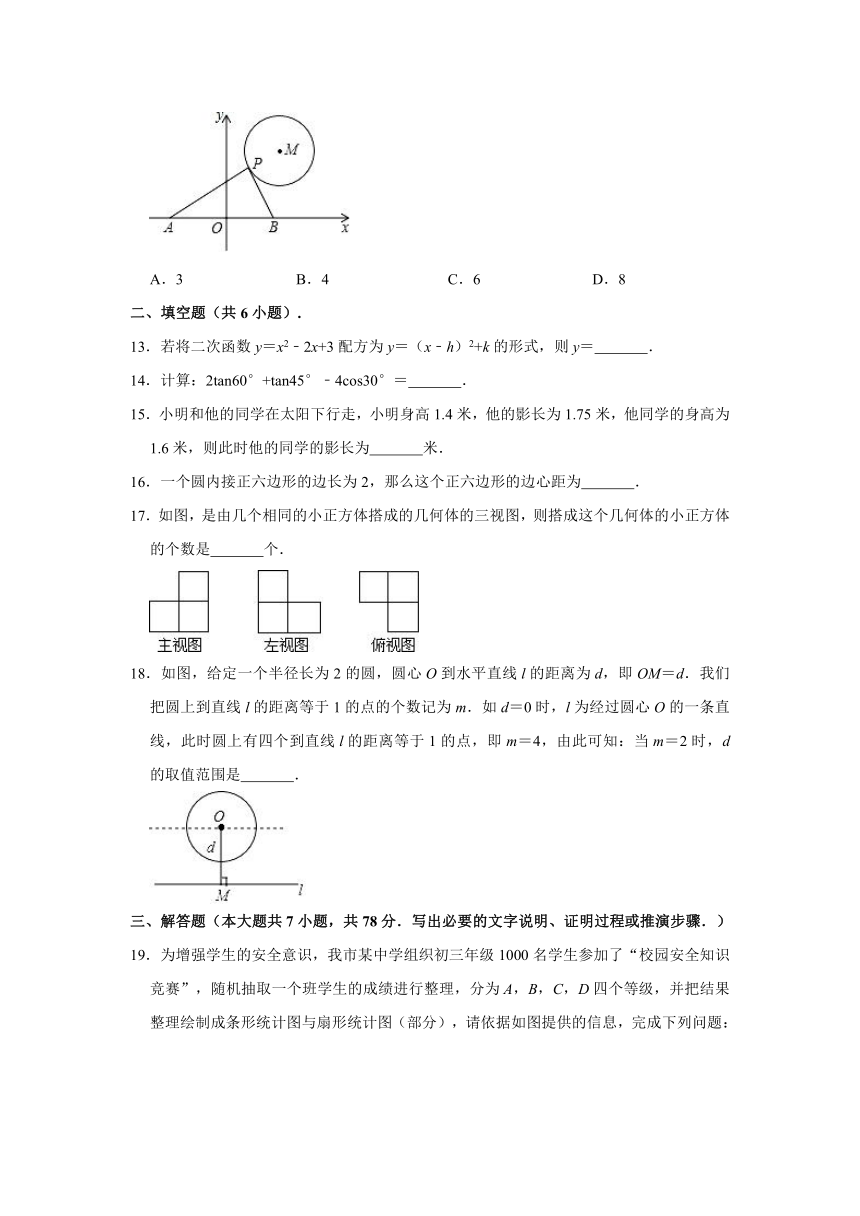
12.如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
二、填空题(共6小题).
13.若将二次函数y=x2﹣2x+3配方为y=(x﹣h)2+k的形式,则y= .
14.计算:2tan60°+tan45°﹣4cos30°= .
15.小明和他的同学在太阳下行走,小明身高1.4米,他的影长为1.75米,他同学的身高为1.6米,则此时他的同学的影长为 米.
16.一个圆内接正六边形的边长为2,那么这个正六边形的边心距为 .
17.如图,是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是 个.
18.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:当m=2时,d的取值范围是 .
三、解答题(本大题共7小题,共78分.写出必要的文字说明、证明过程或推演步骤.)
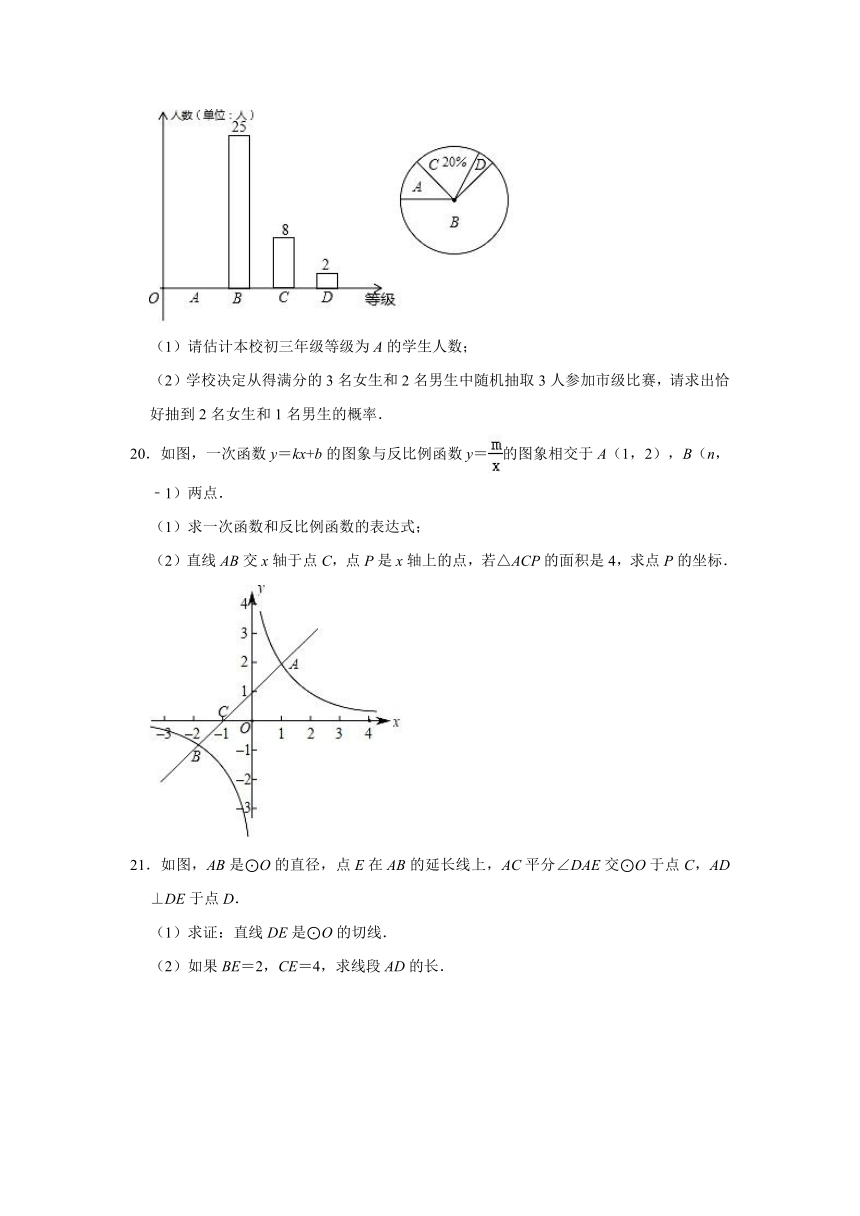
19.为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为A的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
20.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(1,2),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
21.如图,AB是⊙O的直径,点E在AB的延长线上,AC平分∠DAE交⊙O于点C,AD⊥DE于点D.
(1)求证:直线DE是⊙O的切线.
(2)如果BE=2,CE=4,求线段AD的长.
22.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
23.如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)
24.如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°
①求∠OCE的度数;
②若⊙O的半径为2,求线段EF的长.
25.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
参考答案
一、选择题(共12小题).
1.若点A(3,﹣4)、B(﹣2,m)在同一个反比例函数的图象上,则m的值为( )
A.6 B.﹣6 C.12 D.﹣12
【分析】反比例函数的解析式为y=,把A(3,﹣4)代入求出k=﹣12,得出解析式,把B的坐标代入解析式即可.
解:设反比例函数的解析式为y=,
把A(3,﹣4)代入得:k=﹣12,
即y=﹣,
把B(﹣2,m)代入得:m=﹣=6,
故选:A.
2.圆形的物体在太阳光的投影下是( )
A.圆形 B.椭圆形
C.线段 D.以上都有可能
解:根据题意:同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变.
故选:D.
3.袋中有5个白球,有n个红球,从中任意取一个,恰为红球的机会是,则n为( )
A.16 B.10 C.20 D.18
【分析】由袋中有5个白球,有n个红球,从中任意取一个,恰为红球的机会是,根据概率公式,即可得方程:=,解此方程即可求得答案.
解:∵袋中有5个白球,有n个红球,从中任意取一个,恰为红球的机会是,
∴=,
解得:n=10.
故选:B.
4.若点A(﹣2,y1),B(﹣1,y2),C(1,y3)在反比例函数y=﹣的图象上,则下列结论正确的是( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y2>y3>y1
解:∵点A(﹣2,y1),B(﹣1,y2),C(1,y3)都在反比例函数y=﹣的图象上,
∴y1=﹣=3,y2=﹣=6,y3=﹣=﹣6.
∵6>3>﹣6,
∴y2>y1>y3.
故选:A.
5.小明沿着坡度为1:2的山坡向下走了1000m,则他下降了( )
A.200m B.500m C.500m D.1000m
解:由题意得,BC:AB=1:2,
设BC=xm,AB=2xm,
则AC==x=1000,
解得:x=200.
故选:A.
6.用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( )
A.2πcm B.1.5cm C.πcm D.1cm
解:设此圆锥的底面半径为r,
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得,
2πr=,
解得:r=1cm.
故选:D.
7.在 Rt△ABC中,∠C=90°,cosB=,则tanA的值为( )
A. B. C. D.
【分析】利用余弦的定义得到cosB==,设BC=x,AB=3x,则可求出AC=2x,然后根据正切的定义求解.
解:在Rt△ABC中,∠C=90°,
∴cosB==,
设BC=x,AB=3x,则AC=2x,
∴tanA===.
故选:C.
8.如图摆放的几何体的左视图是( )
A. B. C. D.
解:从左边看,是左右边各一个长方形,大小不同,故选C.
9.在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. B.
C. D.
【分析】关键是m的正负的确定,对于二次函数y=ax2+bx+c,当a>0时,开口向上;当a<0时,开口向下.对称轴为x=﹣,与y轴的交点坐标为(0,c).
解:A.由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,对称轴为x=﹣=<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=﹣mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,对称轴为x=﹣=<0,则对称轴应在y轴左侧,与图象符合,故D选项正确.
故选:D.
10.如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长( )米.
A. B. C. D.
解:如图所示:∵第一次是当阳光与地面成45°,
∴AB=BC=5m,
∵第二次是阳光与地面成30°,
∴BD==5(m),
∴第二次观察到的影子比第一次长:(5﹣5)m.
故选:A.
11.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+c<0;④3a+c<0.其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
【分析】由抛物线开口方向得到a>0,然后利用抛物线的对称轴得到b的符号,则可对①进行判断;利用判别式的意义和抛物线与x轴有2个交点可对②进行判断;利用x=1时,y<0可对③进行判断;利用抛物线的对称轴方程得到b=﹣2a,加上x=﹣1时,y>0,即a﹣b+c>0,则可对④进行判断.
解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a<0,
∴ab<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,所以②正确;
∵x=1时,y<0,
∴a+b+c<0,所以③正确;
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a,
而x=﹣1时,y>0,即a﹣b+c>0,
∴a+2a+c>0,所以④错误.
故选:C.
12.如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
解:∵PA⊥PB,
∴∠APB=90°,
∵AO=BO,
∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,
过点M作MQ⊥x轴于点Q,
则OQ=3、MQ=4,
∴OM=5,
又∵MP′=2,
∴OP′=3,
∴AB=2OP′=6,
故选:C.
二、填空题(本大题共6小题,每小题4分,共24分.只要求填写最后结果)
13.若将二次函数y=x2﹣2x+3配方为y=(x﹣h)2+k的形式,则y= (x﹣1)2+2 .
【分析】利用配方法先提出二次项系数,在加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
解:y=x2﹣2x+3=(x2﹣2x+1)+2=(x﹣1)2+2
故本题答案为:y=(x﹣1)2+2.
14.计算:2tan60°+tan45°﹣4cos30°= 1 .
解:原式=2+1﹣4×
=2+1﹣2
=1.
故答案为:1.
15.小明和他的同学在太阳下行走,小明身高1.4米,他的影长为1.75米,他同学的身高为1.6米,则此时他的同学的影长为 2 米.
解:设他的同学的影长为xm,
∵同一时刻物高与影长成正比例,
∴=,
解得:x=2,
∴他的同学的影长为2m,
故答案为:2.
16.一个圆内接正六边形的边长为2,那么这个正六边形的边心距为 .
【分析】根据正六边形的特点,通过中心作边的垂线,连接半径,结合解直角三角形的有关知识解决.
解:如图,连接OA、OB;过点O作OG⊥AB于点G.
在Rt△AOG中,OA=2,∠AOG=30°,
∴OG=OA?cos 30°=2×.
故答案为:.
17.如图,是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是 4 个.
【分析】根据给出的几何体,通过动手操作,观察可得答案为4,也可以根据画三视图的方法,发挥空间想象能力,直接想象出每个位置正方体的数目,再加上来.
解:由三视图可得,需要的小正方体的数目:1+2+1=4.如图:
18.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:当m=2时,d的取值范围是 1<d<3 .
解:当d=3时,m=1;
当d=1时,m=3;
∴当1<d<3时,m=2,
故答案为:1<d<3.
三、解答题(本大题共7小题,共78分.写出必要的文字说明、证明过程或推演步骤.)
19.为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为A的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
解:(1)∵所抽取学生的总数为8÷20%=40人,
∴该班级等级为A的学生人数为40﹣(25+8+2)=5人,
则估计本校初三年级等级为A的学生人数为1000×=125人;
(2)设两位满分的男生记为A1、A2、三位满分的女生记为B1、B2、B3,
从这5名同学中选3人的所有等可能结果为:
(B1,B2,B3)、(A2,B2,B3)、(A2,B1,B3)、(A2,B1,B2)、(A1,B2,B3)、
(A1,B1,B3)、(A1,B1,B2)、(A1,A2,B3)、(A1,A2,B2)、(A1,A2,B1),
其中恰好有2名女生、1名男生的结果有6种,
所以恰好抽到2名女生和1名男生的概率为=.
20.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(1,2),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
【分析】(1)先根据点A坐标求出反比例函数解析式,再求出点B的坐标,继而根据点A、B坐标可得直线解析式;
(2)先根据直线解析式求出点C的坐标,再设P(m,0),知PC=|﹣1﹣m|,根据S△ACP=?PC?yA=4求出m的值即可得出答案.
解:(1)将点A(1,2)代入y=,得:m=2,
∴y=,
当y=﹣1时,x=﹣2,
∴B(﹣2,﹣1),
将A(1,2)、B(﹣2,﹣1)代入y=kx+b,
得:,
解得,
∴y=x+1;
∴一次函数解析式为y=x+1,反比例函数解析式为y=;
(2)在y=x+1中,当y=0时,x+1=0,
解得x=﹣1,
∴C(﹣1,0),
设P(m,0),
则PC=|﹣1﹣m|,
∵S△ACP=?PC?yA=4,
∴×|﹣1﹣m|×2=4,
解得m=3或m=﹣5,
∴点P的坐标为(3,0)或(﹣5,0).
21.如图,AB是⊙O的直径,点E在AB的延长线上,AC平分∠DAE交⊙O于点C,AD⊥DE于点D.
(1)求证:直线DE是⊙O的切线.
(2)如果BE=2,CE=4,求线段AD的长.
【分析】(1)连接OC,由角平分线的性质及等腰三角形的性质得出∠DAC=∠ACO,则AD∥OC,证得∠OCE=90°,则可得出结论;
(2)连接OC,设OC=x,由勾股定理得出x2+42=(2+x)2,证明△COE∽△DAE,由相似三角形的性质可求出答案.
【解答】证明:(1)如图1,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAE,
∴∠DAC=∠OAC,
∴∠DAC=∠ACO,
∴AD∥OC,
∵AD⊥DE,
∴∠ADC=90°,
∴∠OCE=∠ADC,
∴∠OCE=90°,
∴DE是⊙O的切线;
(2)解:如图1,连接OC,
设OC=x,
∵OC2+CE2=OE2,
∴x2+42=(2+x)2,
∴x=3,
∴OC=3,
∵AD∥OC,
∴△COE∽△DAE,
∴,
∴,
∴AD=.
22.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
解:(1)y=(x﹣50)[50+5(100﹣x)]
=(x﹣50)(﹣5x+550)
=﹣5x2+800x﹣27500
∴y=﹣5x2+800x﹣27500(50≤x≤100);
(2)y=﹣5x2+800x﹣27500
=﹣5(x﹣80)2+4500
∵a=﹣5<0,
∴抛物线开口向下.
∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,y最大值=4500;
(3)当y=4000时,﹣5(x﹣80)2+4500=4000,
解得x1=70,x2=90.
∴当70≤x≤90时,每天的销售利润不低于4000元.
由每天的总成本不超过7000元,得50(﹣5x+550)≤7000,
解得x≥82.
∴82≤x≤90,
∵50≤x≤100,
∴销售单价应该控制在82元至90元之间.
23.如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)
【分析】过B分别作AE、DE的垂线,设垂足为F、G.分别在Rt△ABF和Rt△ADE中,通过解直角三角形求出BF、AF、DE的长,进而可求出EF即BG的长;在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长;根据CD=CG+GE﹣DE即可求出宣传牌的高度.
解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,i=tan∠BAF==,
∴∠BAF=30°,
∴BF=AB=5,AF=5.
∴BG=AF+AE=5+15.
Rt△BGC中,∠CBG=45°,
∴CG=BG=5+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=AE=15.
∴CD=CG+GE﹣DE=5+15+5﹣15=20﹣10≈2.7m.
答:宣传牌CD高约2.7米.
24.如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°
①求∠OCE的度数;
②若⊙O的半径为2,求线段EF的长.
解:(1)∵CD是⊙O的切线,
∴OC⊥CD,
∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠OCA,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
∴AC平分∠DAO;
(2)①∵AD∥OC,
∴∠EOC=∠DAO=105°,
∵∠E=30°,
∴∠OCE=45°;
②作OG⊥CE于点G,
则CG=FG=OG,
∵OC=2,∠OCE=45°,
∴CG=OG=2,
∴FG=2,
在Rt△OGE中,∠E=30°,
∴GE=2,
∴.
25.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
【分析】(1)设出抛物线解析式,用待定系数法求解即可;
(2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立函数关系式S四边形APCD=﹣2x2+10x,根据二次函数表达式求出极值;
(3)先判断出△HMN≌△AOE,求出M点的横坐标,从而求出点M,N的坐标.
解:(1)设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5;
(2)当y=0时,﹣x2+4x+5=0,
∴x1=﹣1,x2=5,
∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
由点A、B的坐标得,直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),
∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,
∵AC=4,
∴S四边形APCD=×AC×PD=2(﹣x2+5x)=﹣2x2+10x,
∴当x=时,
∴即点P(,)时,S四边形APCD最大=;
(3)如图,过M作MH垂直于对称轴,垂足为H,
∵MN∥AE,MN=AE,
∴△HMN≌△AOE(AAS),
∴HM=OE=1,
∴M点的横坐标为x=3或x=1,
当x=1时,M点纵坐标为8,
当x=3时,M点纵坐标为8,
∴M点的坐标为M1(1,8)或M2(3,8),
∵A(0,5),E(﹣1,0),
∴直线AE解析式为y=5x+5,
∵MN∥AE,
∴MN的解析式为y=5x+b,
∵点N在抛物线对称轴x=2上,
∴N(2,10+b),
∵AE2=OA2+OE2=26,
∵MN=AE,
∴MN2=AE2,
∴MN2=(2﹣1)2+[8﹣(10+b)]2=1+(b+2)2
∵M点的坐标为M1(1,8)或M2(3,8),
∴点M1,M2关于抛物线对称轴x=2对称,
∵点N在抛物线对称轴上,
∴M1N=M2N,
∴1+(b+2)2=26,
∴b=3,或b=﹣7,
∴10+b=13或10+b=3,
∴当M点的坐标为(1,8)时,N点坐标为(2,13);当M点的坐标为(3,8)时,N点坐标为(2,3).
一、选择题(共12小题).
1.若点A(3,﹣4)、B(﹣2,m)在同一个反比例函数的图象上,则m的值为( )
A.6 B.﹣6 C.12 D.﹣12
2.圆形的物体在太阳光的投影下是( )
A.圆形 B.椭圆形
C.线段 D.以上都有可能
3.袋中有5个白球,有n个红球,从中任意取一个,恰为红球的机会是,则n为( )
A.16 B.10 C.20 D.18
4.若点A(﹣2,y1),B(﹣1,y2),C(1,y3)在反比例函数y=﹣的图象上,则下列结论正确的是( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y2>y3>y1
5.小明沿着坡度为1:2的山坡向下走了1000m,则他下降了( )
A.200m B.500m C.500m D.1000m
6.用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( )
A.2πcm B.1.5cm C.πcm D.1cm
7.在 Rt△ABC中,∠C=90°,cosB=,则tanA的值为( )
A. B. C. D.
8.如图摆放的几何体的左视图是( )
A. B. C. D.
9.在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. B.
C. D.
10.如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长( )米.
A. B. C. D.
11.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+c<0;④3a+c<0.其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
12.如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
二、填空题(共6小题).
13.若将二次函数y=x2﹣2x+3配方为y=(x﹣h)2+k的形式,则y= .
14.计算:2tan60°+tan45°﹣4cos30°= .
15.小明和他的同学在太阳下行走,小明身高1.4米,他的影长为1.75米,他同学的身高为1.6米,则此时他的同学的影长为 米.
16.一个圆内接正六边形的边长为2,那么这个正六边形的边心距为 .
17.如图,是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是 个.
18.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:当m=2时,d的取值范围是 .
三、解答题(本大题共7小题,共78分.写出必要的文字说明、证明过程或推演步骤.)
19.为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为A的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
20.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(1,2),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
21.如图,AB是⊙O的直径,点E在AB的延长线上,AC平分∠DAE交⊙O于点C,AD⊥DE于点D.
(1)求证:直线DE是⊙O的切线.
(2)如果BE=2,CE=4,求线段AD的长.
22.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
23.如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)
24.如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°
①求∠OCE的度数;
②若⊙O的半径为2,求线段EF的长.
25.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
参考答案
一、选择题(共12小题).
1.若点A(3,﹣4)、B(﹣2,m)在同一个反比例函数的图象上,则m的值为( )
A.6 B.﹣6 C.12 D.﹣12
【分析】反比例函数的解析式为y=,把A(3,﹣4)代入求出k=﹣12,得出解析式,把B的坐标代入解析式即可.
解:设反比例函数的解析式为y=,
把A(3,﹣4)代入得:k=﹣12,
即y=﹣,
把B(﹣2,m)代入得:m=﹣=6,
故选:A.
2.圆形的物体在太阳光的投影下是( )
A.圆形 B.椭圆形
C.线段 D.以上都有可能
解:根据题意:同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变.
故选:D.
3.袋中有5个白球,有n个红球,从中任意取一个,恰为红球的机会是,则n为( )
A.16 B.10 C.20 D.18
【分析】由袋中有5个白球,有n个红球,从中任意取一个,恰为红球的机会是,根据概率公式,即可得方程:=,解此方程即可求得答案.
解:∵袋中有5个白球,有n个红球,从中任意取一个,恰为红球的机会是,
∴=,
解得:n=10.
故选:B.
4.若点A(﹣2,y1),B(﹣1,y2),C(1,y3)在反比例函数y=﹣的图象上,则下列结论正确的是( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y2>y3>y1
解:∵点A(﹣2,y1),B(﹣1,y2),C(1,y3)都在反比例函数y=﹣的图象上,
∴y1=﹣=3,y2=﹣=6,y3=﹣=﹣6.
∵6>3>﹣6,
∴y2>y1>y3.
故选:A.
5.小明沿着坡度为1:2的山坡向下走了1000m,则他下降了( )
A.200m B.500m C.500m D.1000m
解:由题意得,BC:AB=1:2,
设BC=xm,AB=2xm,
则AC==x=1000,
解得:x=200.
故选:A.
6.用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( )
A.2πcm B.1.5cm C.πcm D.1cm
解:设此圆锥的底面半径为r,
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得,
2πr=,
解得:r=1cm.
故选:D.
7.在 Rt△ABC中,∠C=90°,cosB=,则tanA的值为( )
A. B. C. D.
【分析】利用余弦的定义得到cosB==,设BC=x,AB=3x,则可求出AC=2x,然后根据正切的定义求解.
解:在Rt△ABC中,∠C=90°,
∴cosB==,
设BC=x,AB=3x,则AC=2x,
∴tanA===.
故选:C.
8.如图摆放的几何体的左视图是( )
A. B. C. D.
解:从左边看,是左右边各一个长方形,大小不同,故选C.
9.在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. B.
C. D.
【分析】关键是m的正负的确定,对于二次函数y=ax2+bx+c,当a>0时,开口向上;当a<0时,开口向下.对称轴为x=﹣,与y轴的交点坐标为(0,c).
解:A.由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,对称轴为x=﹣=<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=﹣mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,对称轴为x=﹣=<0,则对称轴应在y轴左侧,与图象符合,故D选项正确.
故选:D.
10.如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长( )米.
A. B. C. D.
解:如图所示:∵第一次是当阳光与地面成45°,
∴AB=BC=5m,
∵第二次是阳光与地面成30°,
∴BD==5(m),
∴第二次观察到的影子比第一次长:(5﹣5)m.
故选:A.
11.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+c<0;④3a+c<0.其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
【分析】由抛物线开口方向得到a>0,然后利用抛物线的对称轴得到b的符号,则可对①进行判断;利用判别式的意义和抛物线与x轴有2个交点可对②进行判断;利用x=1时,y<0可对③进行判断;利用抛物线的对称轴方程得到b=﹣2a,加上x=﹣1时,y>0,即a﹣b+c>0,则可对④进行判断.
解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a<0,
∴ab<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,所以②正确;
∵x=1时,y<0,
∴a+b+c<0,所以③正确;
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a,
而x=﹣1时,y>0,即a﹣b+c>0,
∴a+2a+c>0,所以④错误.
故选:C.
12.如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
解:∵PA⊥PB,
∴∠APB=90°,
∵AO=BO,
∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,
过点M作MQ⊥x轴于点Q,
则OQ=3、MQ=4,
∴OM=5,
又∵MP′=2,
∴OP′=3,
∴AB=2OP′=6,
故选:C.
二、填空题(本大题共6小题,每小题4分,共24分.只要求填写最后结果)
13.若将二次函数y=x2﹣2x+3配方为y=(x﹣h)2+k的形式,则y= (x﹣1)2+2 .
【分析】利用配方法先提出二次项系数,在加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
解:y=x2﹣2x+3=(x2﹣2x+1)+2=(x﹣1)2+2
故本题答案为:y=(x﹣1)2+2.
14.计算:2tan60°+tan45°﹣4cos30°= 1 .
解:原式=2+1﹣4×
=2+1﹣2
=1.
故答案为:1.
15.小明和他的同学在太阳下行走,小明身高1.4米,他的影长为1.75米,他同学的身高为1.6米,则此时他的同学的影长为 2 米.
解:设他的同学的影长为xm,
∵同一时刻物高与影长成正比例,
∴=,
解得:x=2,
∴他的同学的影长为2m,
故答案为:2.
16.一个圆内接正六边形的边长为2,那么这个正六边形的边心距为 .
【分析】根据正六边形的特点,通过中心作边的垂线,连接半径,结合解直角三角形的有关知识解决.
解:如图,连接OA、OB;过点O作OG⊥AB于点G.
在Rt△AOG中,OA=2,∠AOG=30°,
∴OG=OA?cos 30°=2×.
故答案为:.
17.如图,是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是 4 个.
【分析】根据给出的几何体,通过动手操作,观察可得答案为4,也可以根据画三视图的方法,发挥空间想象能力,直接想象出每个位置正方体的数目,再加上来.
解:由三视图可得,需要的小正方体的数目:1+2+1=4.如图:
18.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:当m=2时,d的取值范围是 1<d<3 .
解:当d=3时,m=1;
当d=1时,m=3;
∴当1<d<3时,m=2,
故答案为:1<d<3.
三、解答题(本大题共7小题,共78分.写出必要的文字说明、证明过程或推演步骤.)
19.为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为A的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
解:(1)∵所抽取学生的总数为8÷20%=40人,
∴该班级等级为A的学生人数为40﹣(25+8+2)=5人,
则估计本校初三年级等级为A的学生人数为1000×=125人;
(2)设两位满分的男生记为A1、A2、三位满分的女生记为B1、B2、B3,
从这5名同学中选3人的所有等可能结果为:
(B1,B2,B3)、(A2,B2,B3)、(A2,B1,B3)、(A2,B1,B2)、(A1,B2,B3)、
(A1,B1,B3)、(A1,B1,B2)、(A1,A2,B3)、(A1,A2,B2)、(A1,A2,B1),
其中恰好有2名女生、1名男生的结果有6种,
所以恰好抽到2名女生和1名男生的概率为=.
20.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(1,2),B(n,﹣1)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
【分析】(1)先根据点A坐标求出反比例函数解析式,再求出点B的坐标,继而根据点A、B坐标可得直线解析式;
(2)先根据直线解析式求出点C的坐标,再设P(m,0),知PC=|﹣1﹣m|,根据S△ACP=?PC?yA=4求出m的值即可得出答案.
解:(1)将点A(1,2)代入y=,得:m=2,
∴y=,
当y=﹣1时,x=﹣2,
∴B(﹣2,﹣1),
将A(1,2)、B(﹣2,﹣1)代入y=kx+b,
得:,
解得,
∴y=x+1;
∴一次函数解析式为y=x+1,反比例函数解析式为y=;
(2)在y=x+1中,当y=0时,x+1=0,
解得x=﹣1,
∴C(﹣1,0),
设P(m,0),
则PC=|﹣1﹣m|,
∵S△ACP=?PC?yA=4,
∴×|﹣1﹣m|×2=4,
解得m=3或m=﹣5,
∴点P的坐标为(3,0)或(﹣5,0).
21.如图,AB是⊙O的直径,点E在AB的延长线上,AC平分∠DAE交⊙O于点C,AD⊥DE于点D.
(1)求证:直线DE是⊙O的切线.
(2)如果BE=2,CE=4,求线段AD的长.
【分析】(1)连接OC,由角平分线的性质及等腰三角形的性质得出∠DAC=∠ACO,则AD∥OC,证得∠OCE=90°,则可得出结论;
(2)连接OC,设OC=x,由勾股定理得出x2+42=(2+x)2,证明△COE∽△DAE,由相似三角形的性质可求出答案.
【解答】证明:(1)如图1,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAE,
∴∠DAC=∠OAC,
∴∠DAC=∠ACO,
∴AD∥OC,
∵AD⊥DE,
∴∠ADC=90°,
∴∠OCE=∠ADC,
∴∠OCE=90°,
∴DE是⊙O的切线;
(2)解:如图1,连接OC,
设OC=x,
∵OC2+CE2=OE2,
∴x2+42=(2+x)2,
∴x=3,
∴OC=3,
∵AD∥OC,
∴△COE∽△DAE,
∴,
∴,
∴AD=.
22.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
解:(1)y=(x﹣50)[50+5(100﹣x)]
=(x﹣50)(﹣5x+550)
=﹣5x2+800x﹣27500
∴y=﹣5x2+800x﹣27500(50≤x≤100);
(2)y=﹣5x2+800x﹣27500
=﹣5(x﹣80)2+4500
∵a=﹣5<0,
∴抛物线开口向下.
∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,y最大值=4500;
(3)当y=4000时,﹣5(x﹣80)2+4500=4000,
解得x1=70,x2=90.
∴当70≤x≤90时,每天的销售利润不低于4000元.
由每天的总成本不超过7000元,得50(﹣5x+550)≤7000,
解得x≥82.
∴82≤x≤90,
∵50≤x≤100,
∴销售单价应该控制在82元至90元之间.
23.如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)
【分析】过B分别作AE、DE的垂线,设垂足为F、G.分别在Rt△ABF和Rt△ADE中,通过解直角三角形求出BF、AF、DE的长,进而可求出EF即BG的长;在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长;根据CD=CG+GE﹣DE即可求出宣传牌的高度.
解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,i=tan∠BAF==,
∴∠BAF=30°,
∴BF=AB=5,AF=5.
∴BG=AF+AE=5+15.
Rt△BGC中,∠CBG=45°,
∴CG=BG=5+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=AE=15.
∴CD=CG+GE﹣DE=5+15+5﹣15=20﹣10≈2.7m.
答:宣传牌CD高约2.7米.
24.如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°
①求∠OCE的度数;
②若⊙O的半径为2,求线段EF的长.
解:(1)∵CD是⊙O的切线,
∴OC⊥CD,
∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠OCA,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
∴AC平分∠DAO;
(2)①∵AD∥OC,
∴∠EOC=∠DAO=105°,
∵∠E=30°,
∴∠OCE=45°;
②作OG⊥CE于点G,
则CG=FG=OG,
∵OC=2,∠OCE=45°,
∴CG=OG=2,
∴FG=2,
在Rt△OGE中,∠E=30°,
∴GE=2,
∴.
25.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
【分析】(1)设出抛物线解析式,用待定系数法求解即可;
(2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立函数关系式S四边形APCD=﹣2x2+10x,根据二次函数表达式求出极值;
(3)先判断出△HMN≌△AOE,求出M点的横坐标,从而求出点M,N的坐标.
解:(1)设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5;
(2)当y=0时,﹣x2+4x+5=0,
∴x1=﹣1,x2=5,
∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
由点A、B的坐标得,直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),
∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,
∵AC=4,
∴S四边形APCD=×AC×PD=2(﹣x2+5x)=﹣2x2+10x,
∴当x=时,
∴即点P(,)时,S四边形APCD最大=;
(3)如图,过M作MH垂直于对称轴,垂足为H,
∵MN∥AE,MN=AE,
∴△HMN≌△AOE(AAS),
∴HM=OE=1,
∴M点的横坐标为x=3或x=1,
当x=1时,M点纵坐标为8,
当x=3时,M点纵坐标为8,
∴M点的坐标为M1(1,8)或M2(3,8),
∵A(0,5),E(﹣1,0),
∴直线AE解析式为y=5x+5,
∵MN∥AE,
∴MN的解析式为y=5x+b,
∵点N在抛物线对称轴x=2上,
∴N(2,10+b),
∵AE2=OA2+OE2=26,
∵MN=AE,
∴MN2=AE2,
∴MN2=(2﹣1)2+[8﹣(10+b)]2=1+(b+2)2
∵M点的坐标为M1(1,8)或M2(3,8),
∴点M1,M2关于抛物线对称轴x=2对称,
∵点N在抛物线对称轴上,
∴M1N=M2N,
∴1+(b+2)2=26,
∴b=3,或b=﹣7,
∴10+b=13或10+b=3,
∴当M点的坐标为(1,8)时,N点坐标为(2,13);当M点的坐标为(3,8)时,N点坐标为(2,3).
同课章节目录
