2020-2021学年山东省烟台市蓬莱实验中学八年级(上)期末数学试卷(五四学制) (Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省烟台市蓬莱实验中学八年级(上)期末数学试卷(五四学制) (Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 721.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 00:00:00 | ||
图片预览




文档简介
2020-2021学年山东省烟台市蓬莱实验中学八年级第一学期期末数学试卷(五四学制)
一.选择题(共10小题).
1.无论x取何值,下列分式总有意义的是( )
A. B. C. D.
2.下列图形是轴对称图形的是( )
A. B. C. D.
3.下列各组数据,能构成三角形的是( )
A.1cm,2cm,3cm B.2cm,2cm,5cm
C.3cm,4cm,5cm D.7cm,5cm,1cm
4.下列运算正确的是( )
A.3a÷a=3 B.(a﹣b)2=a2﹣b2
C.(ab3)2=a2b5 D.(x+y)(y﹣x)=x2﹣y2
5.下列各式中,正确的是( )
A.= B.=
C.=﹣ D.=
6.下列因式分解正确的是( )
A.2ab2﹣4ab=2a(b2﹣2b) B.a2+b2=(a+b)(a﹣b)
C.x2+2xy﹣4y2=(x﹣2y)2 D.﹣my2+4my﹣4m=﹣m(y﹣2)2
7.在△ABC中,AB=BC,两个完全一样的三角尺按如图所示摆放,它们一组较短的直角边分别在AB,BC上,另一组较长的对应边的顶点重合于点P,BP交边AC于点D,则下列结论错误的是( )
A.BP平分∠ABC B.AD=DC
C.BD垂直平分AC D.AB=2AD
8.如图,在△ABC和△DEC中,已知AB=DE,添加下列各组条件后,不能使△ABC≌△DEC的是( )
A.BC=EC,∠B=∠E B.BC=DC,∠A=∠D
C.∠B=∠E,∠A=∠D D.BC=EC,AC=DC
9.随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递80件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件x件,根据题意可列方程为( )
A.= B.+80=
C.=﹣80 D.=
10.△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
A.△ABC的周长 B.△AFH的周长
C.四边形FBGH的周长 D.四边形ADEC的周长
二、填空题(共6小题).
11.将0.00025用科学记数法表示 .
12.一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是 .
13.若am=9,an=3,则am﹣n= .
14.如图,在△ABC中,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M、N,作直线MN分别交BC、AC于点D、E,若△ABC的周长为23cm,△ABD的周长为13cm,则AE为 cm.
15.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
16.关于x的方程x+=a+的两个解为x1=a,x2=,x+=a+的两个解为x1=a,x2=,则关于x的方程x+=a+的两个解为 .
三、解答题(共7小题,共66分)
17.计算:
(1)(2x4)2﹣3x3?4x5;
(2)(a+3)2﹣(a﹣3)(a+3).
18.(1)因式分解:(y2+1)2﹣4y2;
(2)解方程:﹣1=.
19.如图所示的正方形网格中,每个小正方形的边长都为1,△ABC的顶点都在网格线的交点上,点B关于y轴的对称点的坐标为(2,0),点C关于x轴的对称点的坐标为(﹣1,﹣2).
(1)根据上述条件,在网格中建立平面直角坐标系xOy;
(2)画出△ABC关于y轴的对称图形△A1B1C1.
20.近年来,我市大力发展城市快速交通,小王开车从家到单位有两条路线可选择,路线A为全程25km的普通道路,路线B包含快速通道,全程30km,走路线B比走路线A平均速度提高50%,时间节省6min,求走路线B的平均速度.
21.如图,在△ABC中,∠C=90°,在边AB上取一点D,使得BD=AC,过B作AC的平行线BE,过D作AB的垂线与BE交于点E,连接AE.
(1)求证:△ABC≌△BED.
(2)若∠BAC=34°,求∠AED的度数.
22.阅读下面材料:
一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式.例如:a+b+c,abc,a2+b2…,含有两个字母a,b的对称式的基本对称式是a+b和ab,像a2+b2,(a+2)(b+2)等对称式都可以用a+b,ab表示,例如:a2+b2=(a+b)2﹣2ab.
请根据以上材料解决下列问题:
(1)式子①a2b2;②a2﹣b2;③中,属于对称式的是 (填序号);
(2)已知(x+a)(x+b)=x2+mx+n.当m=﹣2,n=时,求对称式的值.
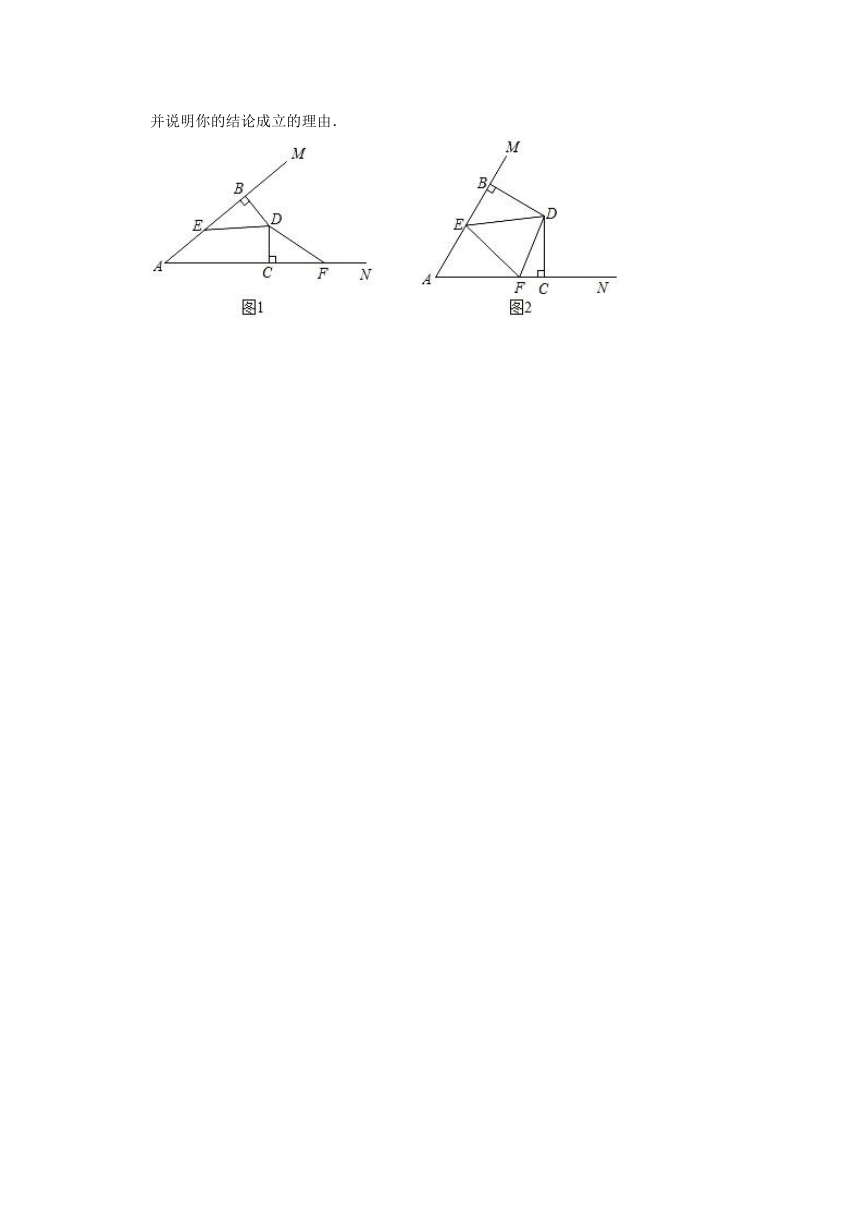
23.在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
参考答案
一.选择题(共10小题).
1.无论x取何值,下列分式总有意义的是( )
A. B. C. D.
解:A.当x=0时该分式无意义,不合题意;
B.当x=时该分式无意义,不合题意;
C.无论x取何值,该分式分母不为零,故总有意义,符合题意;
D.当x=1时该分式无意义,不合题意;
故选:C.
2.下列图形是轴对称图形的是( )
A. B. C. D.
解:A、不是轴对称图形,故本选项不合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不合题意;
D、不是轴对称图形,故本选项不合题意.
故选:B.
3.下列各组数据,能构成三角形的是( )
A.1cm,2cm,3cm B.2cm,2cm,5cm
C.3cm,4cm,5cm D.7cm,5cm,1cm
解:A、1+2=3,不能构成三角形;
B、2+2<5,不能构成三角形;
C、3+4>5,能构成三角形;
D、1+5<7,不能构成三角形.
故选:C.
4.下列运算正确的是( )
A.3a÷a=3 B.(a﹣b)2=a2﹣b2
C.(ab3)2=a2b5 D.(x+y)(y﹣x)=x2﹣y2
解:3a÷a=3,故选项A正确;
(a﹣b)2=a2﹣2ab+b2,故选项B错误;
(ab3)2=a2b6,故选项C错误;
(x+y)(y﹣x)=y2﹣x2,故选项D错误;
故选:A.
5.下列各式中,正确的是( )
A.= B.=
C.=﹣ D.=
解:A、根据分式的基本性质应该分子和分母都除以b,故本选项错误;
B、根据分式的基本性质,分子和分母都加上2不相等,故本选项错误;
C、=﹣,故本选项错误;
D、∵a﹣2≠0,
∴=,故本选项正确;
故选:D.
6.下列因式分解正确的是( )
A.2ab2﹣4ab=2a(b2﹣2b) B.a2+b2=(a+b)(a﹣b)
C.x2+2xy﹣4y2=(x﹣2y)2 D.﹣my2+4my﹣4m=﹣m(y﹣2)2
解:A、原式=2ab(b﹣2),不符合题意;
B、原式不能分解,不符合题意;
C、原式不能分解,不符合题意;
D、原式=﹣m(y﹣2)2,符合题意.
故选:D.
7.在△ABC中,AB=BC,两个完全一样的三角尺按如图所示摆放,它们一组较短的直角边分别在AB,BC上,另一组较长的对应边的顶点重合于点P,BP交边AC于点D,则下列结论错误的是( )
A.BP平分∠ABC B.AD=DC
C.BD垂直平分AC D.AB=2AD
解:如图.
由题意得,PE⊥AB,PF⊥BC,PE=PF,
∴BP平分∠ABC,
∵AB=BC,
∴AD=DC,BD垂直平分AC,
故选项A、B、C正确,不符合题意;
只有当△ABC是等边三角形时,才能得出AB=2AD,
故选项D错误,符合题意.
故选:D.
8.如图,在△ABC和△DEC中,已知AB=DE,添加下列各组条件后,不能使△ABC≌△DEC的是( )
A.BC=EC,∠B=∠E B.BC=DC,∠A=∠D
C.∠B=∠E,∠A=∠D D.BC=EC,AC=DC
解:A、已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC≌△DEC,故此选项不合题意;
B、已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC≌△DEC,故此选项符合题意;
C、已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC≌△DEC,故此选项不合题意;
D、已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC≌△DEC,故此选项不合题意;
故选:B.
9.随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递80件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件x件,根据题意可列方程为( )
A.= B.+80=
C.=﹣80 D.=
解:设原来平均每人每周投递快件x件,则现在平均每人每周投递快件(x+80)件,
依题意,得:=.
故选:D.
10.△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
A.△ABC的周长 B.△AFH的周长
C.四边形FBGH的周长 D.四边形ADEC的周长
解:∵△GFH为等边三角形,
∴FH=GH,∠FHG=60°,
∴∠AHF+∠GHC=120°,
∵△ABC为等边三角形,
∴AB=BC=AC,∠ACB=∠A=60°,
∴∠GHC+∠HGC=120°,
∴∠AHF=∠HGC,
∴△AFH≌△CHG(AAS),
∴AF=CH.
∵△BDE和△FGH是两个全等的等边三角形,
∴BE=FH,
∴五边形DECHF的周长=DE+CE+CH+FH+DF=BD+CE+AF+BE+DF,
=(BD+DF+AF)+(CE+BE),
=AB+BC.
∴只需知道△ABC的周长即可.
故选:A.
二、填空题(共6小题).
11.将0.00025用科学记数法表示 2.5×10﹣4 .
解:将0.00025用科学记数法表示2.5×10﹣4.
故答案为:2.5×10﹣4.
12.一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是 6 .
解:设这个多边形的边数为n,依题意,得:
(n﹣2)?180°=2×360°,
解得,n=6.
故答案为:6.
13.若am=9,an=3,则am﹣n= 3 .
解:∵am=9,an=3,
∴am﹣n=am÷an=9÷3=3.
故答案为:3.
14.如图,在△ABC中,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M、N,作直线MN分别交BC、AC于点D、E,若△ABC的周长为23cm,△ABD的周长为13cm,则AE为 5 cm.
解:由题意可得:MN是线段AC的垂直平分线,
则AE=EC,AD=DC,
∵△ABC的周长为23cm,△ABD的周长为13cm,
∴AB+BC+AC=23cm,AB+BD=AD=AB+BD+DC=AB+BC=13cm,
∴AC=23﹣13=10(cm),
∴AE=AC=5cm.
故答案为:5.
15.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 82° .
解:∵AC平分∠DCB,
∴∠BCA=∠DCA,
又∵CB=CD,AC=AC,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∴∠B+∠ACB=∠D+∠ACD,
∵∠CAE=∠D+∠ACD=49°,
∴∠B+∠ACB=49°,
∴∠BAE=180°﹣∠B﹣∠ACB﹣∠CAE=82°,
故答案为:82°.
16.关于x的方程x+=a+的两个解为x1=a,x2=,x+=a+的两个解为x1=a,x2=,则关于x的方程x+=a+的两个解为 x1=a,x2= .
解:x+=a+可化为:x﹣1+=a﹣1+,
∵方程x+=a+的两个解为x1=a,x2=,
∴x﹣1=a﹣1或x﹣1=,
解得:x1=a,x2=,
经检验x1=a,x2=都是分式方程的解.
故答案为:x1=a,x2=.
三、解答题(本大题共7小题,共66分)
17.计算:
(1)(2x4)2﹣3x3?4x5;
(2)(a+3)2﹣(a﹣3)(a+3).
解:(1)(2x4)2﹣3x3?4x5
=4x8﹣12x8
=﹣8x8;
(2)(a+3)2﹣(a﹣3)(a+3)
=a2+6a+9﹣a2+9
=6a+18.
18.(1)因式分解:(y2+1)2﹣4y2;
(2)解方程:﹣1=.
解:(1)原式=(y2+1+2y)(y2+1﹣2y)
=(y+1)2(y﹣1)2;
(2)去分母得:x2+x﹣x2+1=3,
解得:x=2,
经检验x=2是分式方程的解.
19.如图所示的正方形网格中,每个小正方形的边长都为1,△ABC的顶点都在网格线的交点上,点B关于y轴的对称点的坐标为(2,0),点C关于x轴的对称点的坐标为(﹣1,﹣2).
(1)根据上述条件,在网格中建立平面直角坐标系xOy;
(2)画出△ABC关于y轴的对称图形△A1B1C1.
解:(1)如图,平面直角坐标系即为所求作.
(2)如图,△A1B1C1即为所求作.
20.近年来,我市大力发展城市快速交通,小王开车从家到单位有两条路线可选择,路线A为全程25km的普通道路,路线B包含快速通道,全程30km,走路线B比走路线A平均速度提高50%,时间节省6min,求走路线B的平均速度.
解:设走路线A的平均速度为xkm/h,则走路线B的平均速度为(1+50%)xkm/h,
依题意,得:﹣=,
解得:x=50,
经检验,x=50是原方程的解,且符合题意,
∴(1+50%)x=75.
答:走路线B的平均速度为75km/h.
21.如图,在△ABC中,∠C=90°,在边AB上取一点D,使得BD=AC,过B作AC的平行线BE,过D作AB的垂线与BE交于点E,连接AE.
(1)求证:△ABC≌△BED.
(2)若∠BAC=34°,求∠AED的度数.
【解答】(1)证明:∵BE∥AC,
∴∠BAC=∠EBD,
∵DE⊥AB,
∴∠EDB=90°,
∴∠EDB=∠C,
又∵BD=AC,
∴△ABC≌△BED(ASA).
(2)解:∵△ABC≌△BED,
∴AB=BE,
∴∠EAB=∠AEB,
∵∠BAC=34°,
∴∠EBD=34°,
∴∠EAB===73°,
∴∠AED=90°﹣∠EAB=90°﹣73°=17°.
22.阅读下面材料:
一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式.例如:a+b+c,abc,a2+b2…,含有两个字母a,b的对称式的基本对称式是a+b和ab,像a2+b2,(a+2)(b+2)等对称式都可以用a+b,ab表示,例如:a2+b2=(a+b)2﹣2ab.
请根据以上材料解决下列问题:
(1)式子①a2b2;②a2﹣b2;③中,属于对称式的是 ①③ (填序号);
(2)已知(x+a)(x+b)=x2+mx+n.当m=﹣2,n=时,求对称式的值.
解:(1)式子①a2b2②a2﹣b2③中,属于对称式的是①③.
故答案为①③;
(2)∵x2+(a+b)x+ab=x2+mx+n,
∴a+b=m,ab=n.
当m=﹣2,n=时,a+b=﹣2,ab=,
∴====6.
23.在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
解:(1)∵DB⊥AM,DC⊥AN,
∴∠DBE=∠DCF=90°,
在△BDE和△CDF中,
∵
∴△BDE≌△CDF(AAS).
∴DE=DF;
(2)EF=FC+BE,
理由:过点D作∠CDG=∠BDE,交AN于点G,
在△BDE和△CDG中,
,
∴△BDE≌△CDG(ASA),
∴DE=DG,BE=CG.
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°.
∴∠FDG=∠CDG+∠CDF=60°,
∴∠EDF=∠GDF.
在△EDF和△GDF中,
,
∴△EDF≌△GDF(SAS).
∴EF=GF,
∴EF=FC+CG=FC+BE.
一.选择题(共10小题).
1.无论x取何值,下列分式总有意义的是( )
A. B. C. D.
2.下列图形是轴对称图形的是( )
A. B. C. D.
3.下列各组数据,能构成三角形的是( )
A.1cm,2cm,3cm B.2cm,2cm,5cm
C.3cm,4cm,5cm D.7cm,5cm,1cm
4.下列运算正确的是( )
A.3a÷a=3 B.(a﹣b)2=a2﹣b2
C.(ab3)2=a2b5 D.(x+y)(y﹣x)=x2﹣y2
5.下列各式中,正确的是( )
A.= B.=
C.=﹣ D.=
6.下列因式分解正确的是( )
A.2ab2﹣4ab=2a(b2﹣2b) B.a2+b2=(a+b)(a﹣b)
C.x2+2xy﹣4y2=(x﹣2y)2 D.﹣my2+4my﹣4m=﹣m(y﹣2)2
7.在△ABC中,AB=BC,两个完全一样的三角尺按如图所示摆放,它们一组较短的直角边分别在AB,BC上,另一组较长的对应边的顶点重合于点P,BP交边AC于点D,则下列结论错误的是( )
A.BP平分∠ABC B.AD=DC
C.BD垂直平分AC D.AB=2AD
8.如图,在△ABC和△DEC中,已知AB=DE,添加下列各组条件后,不能使△ABC≌△DEC的是( )
A.BC=EC,∠B=∠E B.BC=DC,∠A=∠D
C.∠B=∠E,∠A=∠D D.BC=EC,AC=DC
9.随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递80件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件x件,根据题意可列方程为( )
A.= B.+80=
C.=﹣80 D.=
10.△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
A.△ABC的周长 B.△AFH的周长
C.四边形FBGH的周长 D.四边形ADEC的周长
二、填空题(共6小题).
11.将0.00025用科学记数法表示 .
12.一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是 .
13.若am=9,an=3,则am﹣n= .
14.如图,在△ABC中,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M、N,作直线MN分别交BC、AC于点D、E,若△ABC的周长为23cm,△ABD的周长为13cm,则AE为 cm.
15.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
16.关于x的方程x+=a+的两个解为x1=a,x2=,x+=a+的两个解为x1=a,x2=,则关于x的方程x+=a+的两个解为 .
三、解答题(共7小题,共66分)
17.计算:
(1)(2x4)2﹣3x3?4x5;
(2)(a+3)2﹣(a﹣3)(a+3).
18.(1)因式分解:(y2+1)2﹣4y2;
(2)解方程:﹣1=.
19.如图所示的正方形网格中,每个小正方形的边长都为1,△ABC的顶点都在网格线的交点上,点B关于y轴的对称点的坐标为(2,0),点C关于x轴的对称点的坐标为(﹣1,﹣2).
(1)根据上述条件,在网格中建立平面直角坐标系xOy;
(2)画出△ABC关于y轴的对称图形△A1B1C1.
20.近年来,我市大力发展城市快速交通,小王开车从家到单位有两条路线可选择,路线A为全程25km的普通道路,路线B包含快速通道,全程30km,走路线B比走路线A平均速度提高50%,时间节省6min,求走路线B的平均速度.
21.如图,在△ABC中,∠C=90°,在边AB上取一点D,使得BD=AC,过B作AC的平行线BE,过D作AB的垂线与BE交于点E,连接AE.
(1)求证:△ABC≌△BED.
(2)若∠BAC=34°,求∠AED的度数.
22.阅读下面材料:
一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式.例如:a+b+c,abc,a2+b2…,含有两个字母a,b的对称式的基本对称式是a+b和ab,像a2+b2,(a+2)(b+2)等对称式都可以用a+b,ab表示,例如:a2+b2=(a+b)2﹣2ab.
请根据以上材料解决下列问题:
(1)式子①a2b2;②a2﹣b2;③中,属于对称式的是 (填序号);
(2)已知(x+a)(x+b)=x2+mx+n.当m=﹣2,n=时,求对称式的值.
23.在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
参考答案
一.选择题(共10小题).
1.无论x取何值,下列分式总有意义的是( )
A. B. C. D.
解:A.当x=0时该分式无意义,不合题意;
B.当x=时该分式无意义,不合题意;
C.无论x取何值,该分式分母不为零,故总有意义,符合题意;
D.当x=1时该分式无意义,不合题意;
故选:C.
2.下列图形是轴对称图形的是( )
A. B. C. D.
解:A、不是轴对称图形,故本选项不合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不合题意;
D、不是轴对称图形,故本选项不合题意.
故选:B.
3.下列各组数据,能构成三角形的是( )
A.1cm,2cm,3cm B.2cm,2cm,5cm
C.3cm,4cm,5cm D.7cm,5cm,1cm
解:A、1+2=3,不能构成三角形;
B、2+2<5,不能构成三角形;
C、3+4>5,能构成三角形;
D、1+5<7,不能构成三角形.
故选:C.
4.下列运算正确的是( )
A.3a÷a=3 B.(a﹣b)2=a2﹣b2
C.(ab3)2=a2b5 D.(x+y)(y﹣x)=x2﹣y2
解:3a÷a=3,故选项A正确;
(a﹣b)2=a2﹣2ab+b2,故选项B错误;
(ab3)2=a2b6,故选项C错误;
(x+y)(y﹣x)=y2﹣x2,故选项D错误;
故选:A.
5.下列各式中,正确的是( )
A.= B.=
C.=﹣ D.=
解:A、根据分式的基本性质应该分子和分母都除以b,故本选项错误;
B、根据分式的基本性质,分子和分母都加上2不相等,故本选项错误;
C、=﹣,故本选项错误;
D、∵a﹣2≠0,
∴=,故本选项正确;
故选:D.
6.下列因式分解正确的是( )
A.2ab2﹣4ab=2a(b2﹣2b) B.a2+b2=(a+b)(a﹣b)
C.x2+2xy﹣4y2=(x﹣2y)2 D.﹣my2+4my﹣4m=﹣m(y﹣2)2
解:A、原式=2ab(b﹣2),不符合题意;
B、原式不能分解,不符合题意;
C、原式不能分解,不符合题意;
D、原式=﹣m(y﹣2)2,符合题意.
故选:D.
7.在△ABC中,AB=BC,两个完全一样的三角尺按如图所示摆放,它们一组较短的直角边分别在AB,BC上,另一组较长的对应边的顶点重合于点P,BP交边AC于点D,则下列结论错误的是( )
A.BP平分∠ABC B.AD=DC
C.BD垂直平分AC D.AB=2AD
解:如图.
由题意得,PE⊥AB,PF⊥BC,PE=PF,
∴BP平分∠ABC,
∵AB=BC,
∴AD=DC,BD垂直平分AC,
故选项A、B、C正确,不符合题意;
只有当△ABC是等边三角形时,才能得出AB=2AD,
故选项D错误,符合题意.
故选:D.
8.如图,在△ABC和△DEC中,已知AB=DE,添加下列各组条件后,不能使△ABC≌△DEC的是( )
A.BC=EC,∠B=∠E B.BC=DC,∠A=∠D
C.∠B=∠E,∠A=∠D D.BC=EC,AC=DC
解:A、已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC≌△DEC,故此选项不合题意;
B、已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC≌△DEC,故此选项符合题意;
C、已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC≌△DEC,故此选项不合题意;
D、已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC≌△DEC,故此选项不合题意;
故选:B.
9.随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递80件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件x件,根据题意可列方程为( )
A.= B.+80=
C.=﹣80 D.=
解:设原来平均每人每周投递快件x件,则现在平均每人每周投递快件(x+80)件,
依题意,得:=.
故选:D.
10.△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
A.△ABC的周长 B.△AFH的周长
C.四边形FBGH的周长 D.四边形ADEC的周长
解:∵△GFH为等边三角形,
∴FH=GH,∠FHG=60°,
∴∠AHF+∠GHC=120°,
∵△ABC为等边三角形,
∴AB=BC=AC,∠ACB=∠A=60°,
∴∠GHC+∠HGC=120°,
∴∠AHF=∠HGC,
∴△AFH≌△CHG(AAS),
∴AF=CH.
∵△BDE和△FGH是两个全等的等边三角形,
∴BE=FH,
∴五边形DECHF的周长=DE+CE+CH+FH+DF=BD+CE+AF+BE+DF,
=(BD+DF+AF)+(CE+BE),
=AB+BC.
∴只需知道△ABC的周长即可.
故选:A.
二、填空题(共6小题).
11.将0.00025用科学记数法表示 2.5×10﹣4 .
解:将0.00025用科学记数法表示2.5×10﹣4.
故答案为:2.5×10﹣4.
12.一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是 6 .
解:设这个多边形的边数为n,依题意,得:
(n﹣2)?180°=2×360°,
解得,n=6.
故答案为:6.
13.若am=9,an=3,则am﹣n= 3 .
解:∵am=9,an=3,
∴am﹣n=am÷an=9÷3=3.
故答案为:3.
14.如图,在△ABC中,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M、N,作直线MN分别交BC、AC于点D、E,若△ABC的周长为23cm,△ABD的周长为13cm,则AE为 5 cm.
解:由题意可得:MN是线段AC的垂直平分线,
则AE=EC,AD=DC,
∵△ABC的周长为23cm,△ABD的周长为13cm,
∴AB+BC+AC=23cm,AB+BD=AD=AB+BD+DC=AB+BC=13cm,
∴AC=23﹣13=10(cm),
∴AE=AC=5cm.
故答案为:5.
15.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 82° .
解:∵AC平分∠DCB,
∴∠BCA=∠DCA,
又∵CB=CD,AC=AC,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∴∠B+∠ACB=∠D+∠ACD,
∵∠CAE=∠D+∠ACD=49°,
∴∠B+∠ACB=49°,
∴∠BAE=180°﹣∠B﹣∠ACB﹣∠CAE=82°,
故答案为:82°.
16.关于x的方程x+=a+的两个解为x1=a,x2=,x+=a+的两个解为x1=a,x2=,则关于x的方程x+=a+的两个解为 x1=a,x2= .
解:x+=a+可化为:x﹣1+=a﹣1+,
∵方程x+=a+的两个解为x1=a,x2=,
∴x﹣1=a﹣1或x﹣1=,
解得:x1=a,x2=,
经检验x1=a,x2=都是分式方程的解.
故答案为:x1=a,x2=.
三、解答题(本大题共7小题,共66分)
17.计算:
(1)(2x4)2﹣3x3?4x5;
(2)(a+3)2﹣(a﹣3)(a+3).
解:(1)(2x4)2﹣3x3?4x5
=4x8﹣12x8
=﹣8x8;
(2)(a+3)2﹣(a﹣3)(a+3)
=a2+6a+9﹣a2+9
=6a+18.
18.(1)因式分解:(y2+1)2﹣4y2;
(2)解方程:﹣1=.
解:(1)原式=(y2+1+2y)(y2+1﹣2y)
=(y+1)2(y﹣1)2;
(2)去分母得:x2+x﹣x2+1=3,
解得:x=2,
经检验x=2是分式方程的解.
19.如图所示的正方形网格中,每个小正方形的边长都为1,△ABC的顶点都在网格线的交点上,点B关于y轴的对称点的坐标为(2,0),点C关于x轴的对称点的坐标为(﹣1,﹣2).
(1)根据上述条件,在网格中建立平面直角坐标系xOy;
(2)画出△ABC关于y轴的对称图形△A1B1C1.
解:(1)如图,平面直角坐标系即为所求作.
(2)如图,△A1B1C1即为所求作.
20.近年来,我市大力发展城市快速交通,小王开车从家到单位有两条路线可选择,路线A为全程25km的普通道路,路线B包含快速通道,全程30km,走路线B比走路线A平均速度提高50%,时间节省6min,求走路线B的平均速度.
解:设走路线A的平均速度为xkm/h,则走路线B的平均速度为(1+50%)xkm/h,
依题意,得:﹣=,
解得:x=50,
经检验,x=50是原方程的解,且符合题意,
∴(1+50%)x=75.
答:走路线B的平均速度为75km/h.
21.如图,在△ABC中,∠C=90°,在边AB上取一点D,使得BD=AC,过B作AC的平行线BE,过D作AB的垂线与BE交于点E,连接AE.
(1)求证:△ABC≌△BED.
(2)若∠BAC=34°,求∠AED的度数.
【解答】(1)证明:∵BE∥AC,
∴∠BAC=∠EBD,
∵DE⊥AB,
∴∠EDB=90°,
∴∠EDB=∠C,
又∵BD=AC,
∴△ABC≌△BED(ASA).
(2)解:∵△ABC≌△BED,
∴AB=BE,
∴∠EAB=∠AEB,
∵∠BAC=34°,
∴∠EBD=34°,
∴∠EAB===73°,
∴∠AED=90°﹣∠EAB=90°﹣73°=17°.
22.阅读下面材料:
一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式.例如:a+b+c,abc,a2+b2…,含有两个字母a,b的对称式的基本对称式是a+b和ab,像a2+b2,(a+2)(b+2)等对称式都可以用a+b,ab表示,例如:a2+b2=(a+b)2﹣2ab.
请根据以上材料解决下列问题:
(1)式子①a2b2;②a2﹣b2;③中,属于对称式的是 ①③ (填序号);
(2)已知(x+a)(x+b)=x2+mx+n.当m=﹣2,n=时,求对称式的值.
解:(1)式子①a2b2②a2﹣b2③中,属于对称式的是①③.
故答案为①③;
(2)∵x2+(a+b)x+ab=x2+mx+n,
∴a+b=m,ab=n.
当m=﹣2,n=时,a+b=﹣2,ab=,
∴====6.
23.在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
解:(1)∵DB⊥AM,DC⊥AN,
∴∠DBE=∠DCF=90°,
在△BDE和△CDF中,
∵
∴△BDE≌△CDF(AAS).
∴DE=DF;
(2)EF=FC+BE,
理由:过点D作∠CDG=∠BDE,交AN于点G,
在△BDE和△CDG中,
,
∴△BDE≌△CDG(ASA),
∴DE=DG,BE=CG.
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°.
∴∠FDG=∠CDG+∠CDF=60°,
∴∠EDF=∠GDF.
在△EDF和△GDF中,
,
∴△EDF≌△GDF(SAS).
∴EF=GF,
∴EF=FC+CG=FC+BE.
同课章节目录
