九年级数学下册《反比例函数》测试卷
图片预览


文档简介
九年级数学下册《反比例函数》测试卷
班级 学号 姓名 .
一、填空题(每小题3分,共39分)
1、如果一次函数的图象经过点(),那么 .
2、若反比例函数= 经过点(),则一次函数的图象一定不经过第_____象限.
3、直线与轴交于点(),则 .
4、反比例函数的图象必过点(1,__).
5、已知函数,当>0时,函数图像在第 象限.
6、已知是反比例函数,则的值是 .
7、老师给出一个函数,甲、乙、丙各正确指出了这个函数的一个性质:
甲:函数的图象经过第一象限;乙:函数的图象经过第三象限;丙:在每个象限内,随的增大而减小,请你根据他们的叙述构造满足上述性质的一个函数: .
8、函数的图像,在每一个象限内,随x的增大而 .
9、点既在反比例函数的图象上,又在一次函数的图象上,则以为根的一元二次方程为_________________.
10.如果反比例函数图象过点,那么这个反比例函数的图象在第_______象限.
11、反比例函数 (是常数,)的图象经过点 , 那么_____0(填“>”或“<”).
12、若函数与的图象相交于第一、三象限,则的取值范围是 .
13、点A()、B()、C()在双曲线
上,则的大小关系为__________.
(用“<”将连接起来)
二、选择题(每小题3分,共45分)
题号 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
答案
14、如果双曲线=经过点(),那么此双曲线也经过点
、() 、() 、() 、
15、若点(-1,2)是反比例函数图象上一点,则k的值是
、- 、 、-2 、2
16、直线与曲线的两个交点的坐标是
、(-2,1),(1,2) 、(-2,-1),(1,2)
、(2,-1)(-1,-2) 、(-2,1)(1,-2)
17、在平面直角坐标系中,给出下面四个点,其中在直线上的点是
、(–1,–1) 、 (–2,–5) 、(2,–3)、(4,9)
18、已知反比例函数的图象经过点(1,2),则函数可确定为
、 、 、 、
19、已知函数中,当时,随的增大而增大,则的大致图象为
图1
20、已知反比例函数当时,y 随x的增大面增大,那么一次函数的图象经过
、第一、二、三象限 、第一、二、四象限、第一、三、四象限 、第二、三、四象限
21、在地表以下不太深的地方,温度y(℃)与所处的深度x(km)之间的关系可以近似用 关系式表示,这个关系式符合的数学模型是.
、正比例函数 、反比例函数.
、二次函数 、一次函数
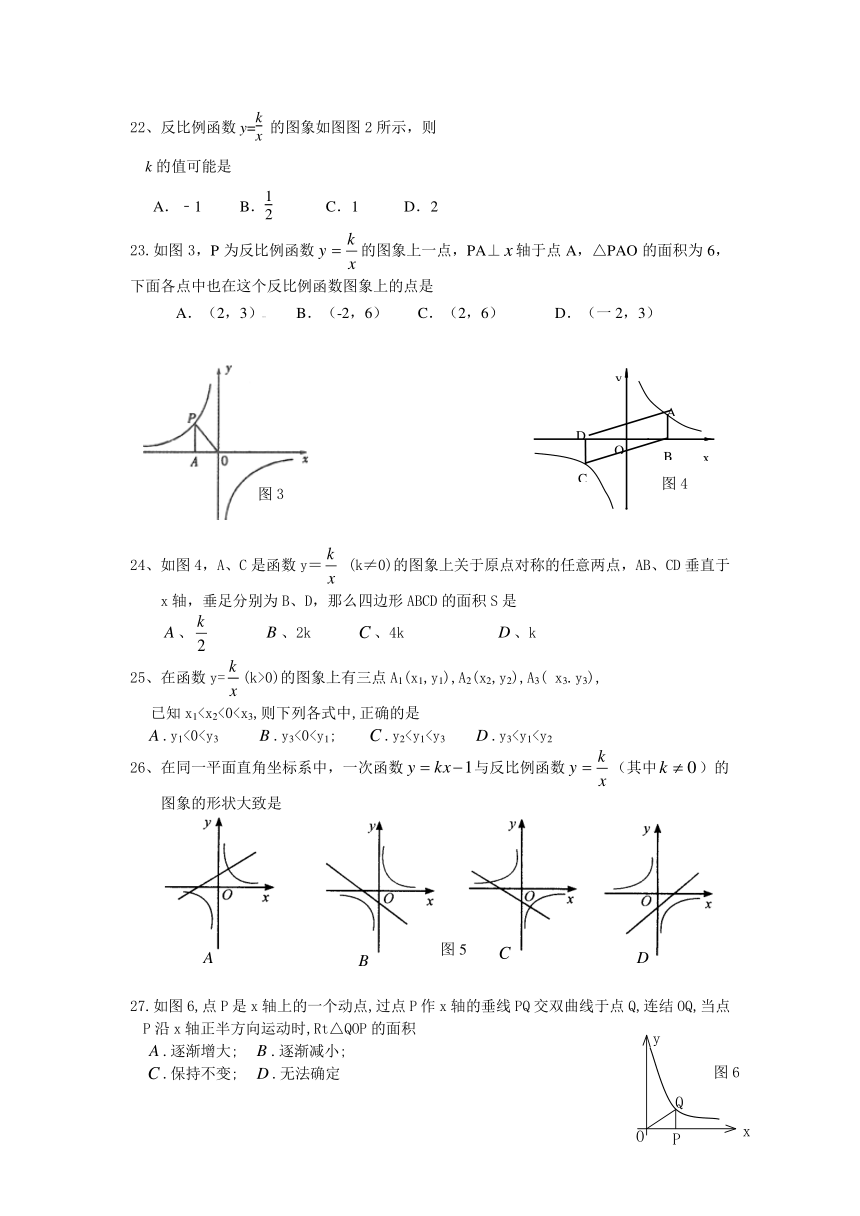
22、反比例函数y=的图象如图图2所示,则
k的值可能是
A.﹣1 B. C.1 D.2
23.如图3,P为反比例函数的图象上一点,PA⊥轴于点A,△PAO的面积为6,下面各点中也在这个反比例函数图象上的点是
A.(2,3) B.(-2,6) C.(2,6) D.(一2,3)
24、如图4,A、C是函数y= (k≠0)的图象上关于原点对称的任意两点,AB、CD垂直于x轴,垂足分别为B、D,那么四边形ABCD的面积S是
、 、2k 、4k 、k
25、在函数y=(k>0)的图象上有三点A1(x1,y1),A2(x2,y2),A3( x3.y3),
已知x1.y1<026、在同一平面直角坐标系中,一次函数与反比例函数(其中)的图象的形状大致是
27.如图6,点P是x轴上的一个动点,过点P作x轴的垂线PQ交双曲线于点Q,连结OQ,当点P沿x轴正半方向运动时,Rt△QOP的面积
.逐渐增大; .逐渐减小;
.保持不变; .无法确定
28.已知直线y=kx+b与双曲线y=交于A(x1,y1),B(x2,y2) 两点,
则x1·x2的值
.与k有关、与b无关; .与k无关、与b无关;
.与k、b都有关; .与k、b都无关
三、解答题
29.为了预防“非典”,某学校对教室采用药薰消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示),现测得药物8分钟燃毕, 此时室内空气中每立方米的含药量为6毫克.请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时y 关于x 的函数关系式为: _____________,
自变量x 的取值范围是:________________;
药物燃烧后y关于x的函数关系式为:___________________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过_______分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10 分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效 为什么
30.已知一次函数y=x+m与反比例函数y=(m≠-1)的图象在第一象限内的交点为P(x0,3).
(1)求x0的值;
(2)求一次函数和反比例函数的解析式.
31.如图,,已知反比例函数y=的图象与一次函数y=kx-4的图象相交于P、Q两点,并且P点的纵坐标是6.
(1)求这个一次函数的解析式;(2)求△POQ的面积.
32、如图,已知一次函数y=-x+8和反比例函数y=(k≠0)的图象在第一象限内有两个不同的公共点A、B.
⑴求实数k的取值范围;
⑵若k=12,求△AOB 的面积.
参考答案:
一、填空题(每小题3分,共39分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13
答案 -2 四 1 5 一、三 -1 不唯一 增大 一、三 < << <<
题号 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
答案 C C B B A A B D B B B C C C D
29、
⑴ () (2) 30分钟 ⑶ 有效
30、⑴ 1 (2)
31、⑴ (2)4
32、⑴<16 (2)16
图2
图3
A
B
C
D
O
x
y
图4
、
、
、
、
图5
图6
P
Q
A
B
C
O
x
y
班级 学号 姓名 .
一、填空题(每小题3分,共39分)
1、如果一次函数的图象经过点(),那么 .
2、若反比例函数= 经过点(),则一次函数的图象一定不经过第_____象限.
3、直线与轴交于点(),则 .
4、反比例函数的图象必过点(1,__).
5、已知函数,当>0时,函数图像在第 象限.
6、已知是反比例函数,则的值是 .
7、老师给出一个函数,甲、乙、丙各正确指出了这个函数的一个性质:
甲:函数的图象经过第一象限;乙:函数的图象经过第三象限;丙:在每个象限内,随的增大而减小,请你根据他们的叙述构造满足上述性质的一个函数: .
8、函数的图像,在每一个象限内,随x的增大而 .
9、点既在反比例函数的图象上,又在一次函数的图象上,则以为根的一元二次方程为_________________.
10.如果反比例函数图象过点,那么这个反比例函数的图象在第_______象限.
11、反比例函数 (是常数,)的图象经过点 , 那么_____0(填“>”或“<”).
12、若函数与的图象相交于第一、三象限,则的取值范围是 .
13、点A()、B()、C()在双曲线
上,则的大小关系为__________.
(用“<”将连接起来)
二、选择题(每小题3分,共45分)
题号 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
答案
14、如果双曲线=经过点(),那么此双曲线也经过点
、() 、() 、() 、
15、若点(-1,2)是反比例函数图象上一点,则k的值是
、- 、 、-2 、2
16、直线与曲线的两个交点的坐标是
、(-2,1),(1,2) 、(-2,-1),(1,2)
、(2,-1)(-1,-2) 、(-2,1)(1,-2)
17、在平面直角坐标系中,给出下面四个点,其中在直线上的点是
、(–1,–1) 、 (–2,–5) 、(2,–3)、(4,9)
18、已知反比例函数的图象经过点(1,2),则函数可确定为
、 、 、 、
19、已知函数中,当时,随的增大而增大,则的大致图象为
图1
20、已知反比例函数当时,y 随x的增大面增大,那么一次函数的图象经过
、第一、二、三象限 、第一、二、四象限、第一、三、四象限 、第二、三、四象限
21、在地表以下不太深的地方,温度y(℃)与所处的深度x(km)之间的关系可以近似用 关系式表示,这个关系式符合的数学模型是.
、正比例函数 、反比例函数.
、二次函数 、一次函数
22、反比例函数y=的图象如图图2所示,则
k的值可能是
A.﹣1 B. C.1 D.2
23.如图3,P为反比例函数的图象上一点,PA⊥轴于点A,△PAO的面积为6,下面各点中也在这个反比例函数图象上的点是
A.(2,3) B.(-2,6) C.(2,6) D.(一2,3)
24、如图4,A、C是函数y= (k≠0)的图象上关于原点对称的任意两点,AB、CD垂直于x轴,垂足分别为B、D,那么四边形ABCD的面积S是
、 、2k 、4k 、k
25、在函数y=(k>0)的图象上有三点A1(x1,y1),A2(x2,y2),A3( x3.y3),
已知x1
27.如图6,点P是x轴上的一个动点,过点P作x轴的垂线PQ交双曲线于点Q,连结OQ,当点P沿x轴正半方向运动时,Rt△QOP的面积
.逐渐增大; .逐渐减小;
.保持不变; .无法确定
28.已知直线y=kx+b与双曲线y=交于A(x1,y1),B(x2,y2) 两点,
则x1·x2的值
.与k有关、与b无关; .与k无关、与b无关;
.与k、b都有关; .与k、b都无关
三、解答题
29.为了预防“非典”,某学校对教室采用药薰消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示),现测得药物8分钟燃毕, 此时室内空气中每立方米的含药量为6毫克.请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时y 关于x 的函数关系式为: _____________,
自变量x 的取值范围是:________________;
药物燃烧后y关于x的函数关系式为:___________________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过_______分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10 分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效 为什么
30.已知一次函数y=x+m与反比例函数y=(m≠-1)的图象在第一象限内的交点为P(x0,3).
(1)求x0的值;
(2)求一次函数和反比例函数的解析式.
31.如图,,已知反比例函数y=的图象与一次函数y=kx-4的图象相交于P、Q两点,并且P点的纵坐标是6.
(1)求这个一次函数的解析式;(2)求△POQ的面积.
32、如图,已知一次函数y=-x+8和反比例函数y=(k≠0)的图象在第一象限内有两个不同的公共点A、B.
⑴求实数k的取值范围;
⑵若k=12,求△AOB 的面积.
参考答案:
一、填空题(每小题3分,共39分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13
答案 -2 四 1 5 一、三 -1 不唯一 增大 一、三 < << <<
题号 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
答案 C C B B A A B D B B B C C C D
29、
⑴ () (2) 30分钟 ⑶ 有效
30、⑴ 1 (2)
31、⑴ (2)4
32、⑴<16 (2)16
图2
图3
A
B
C
D
O
x
y
图4
、
、
、
、
图5
图6
P
Q
A
B
C
O
x
y
