相似三角形的判定(1) PPT课件 九年级数学 初三课件
文档属性
| 名称 | 相似三角形的判定(1) PPT课件 九年级数学 初三课件 |  | |
| 格式 | rar | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-31 15:30:52 | ||
图片预览

文档简介
(共10张PPT)
相似三角形的判定(1)
河师大实验中学 张丽霞
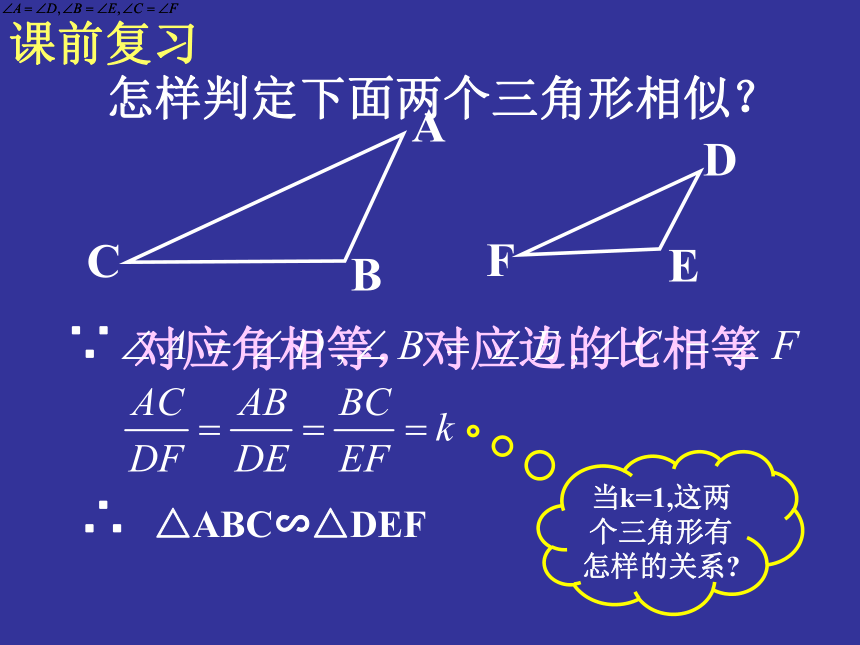
怎样判定下面两个三角形相似?
对应角相等,对应边的比相等
F
D
E
C
A
B
∵
∴
△ABC∽△DEF
当k=1,这两个三角形有怎样的关系
课前复习
A′
B′
C′
10
6
12
51°
82°
A
6
B
C
5
3
82°
47°
6
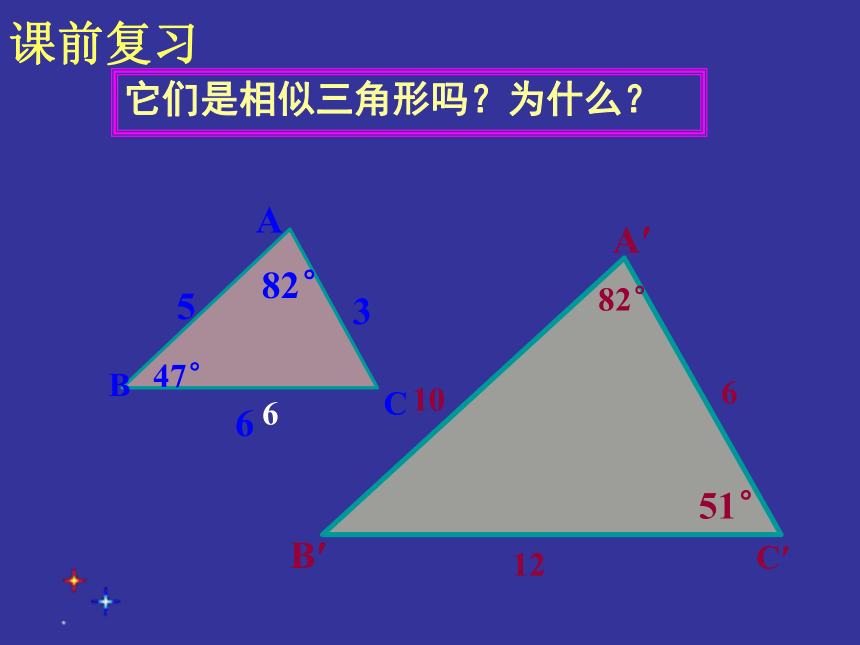
课前复习
它们是相似三角形吗?为什么?
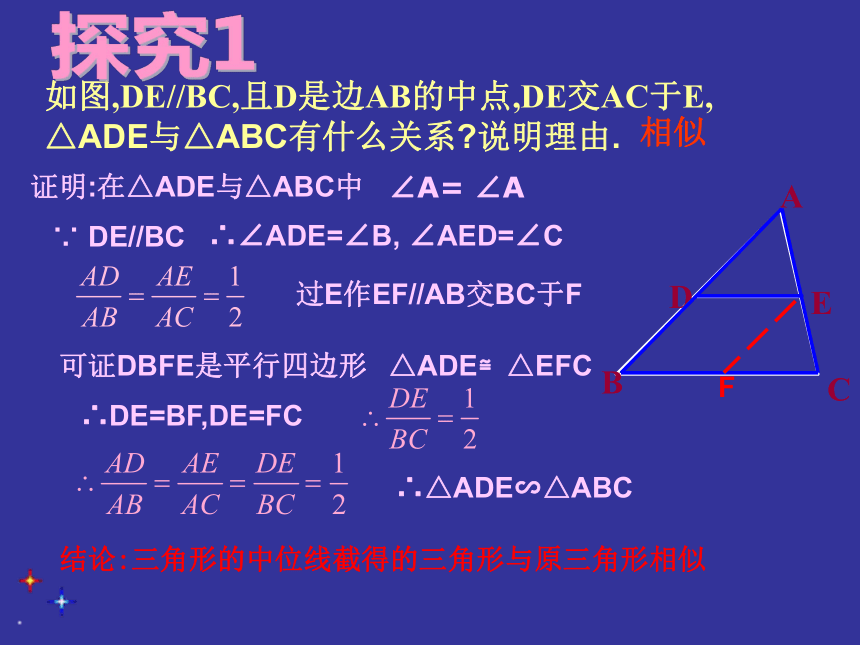
如图,DE//BC,且D是边AB的中点,DE交AC于E, △ADE与△ABC有什么关系 说明理由.
相似
A
B
C
D
E
证明:在△ADE与△ABC中
∠A= ∠A
∵ DE//BC
∴∠ADE=∠B, ∠AED=∠C
过E作EF//AB交BC于F
可证DBFE是平行四边形
F
△ADE≌△EFC
∴DE=BF,DE=FC
∴△ADE∽△ABC
结论:三角形的中位线截得的三角形与原三角形相似
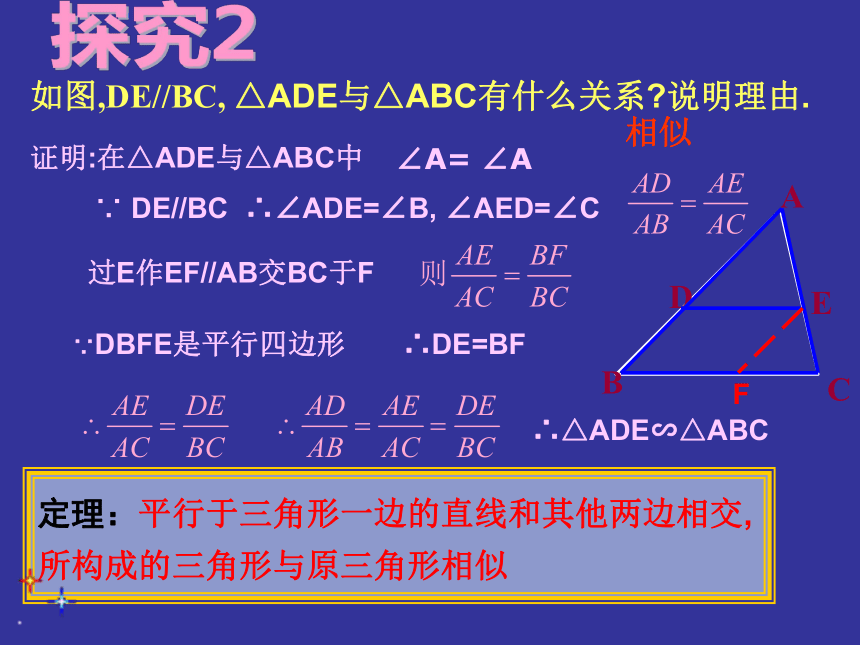
如图,DE//BC, △ADE与△ABC有什么关系 说明理由.
相似
A
B
C
D
E
证明:在△ADE与△ABC中
∠A= ∠A
∵ DE//BC
∴∠ADE=∠B, ∠AED=∠C
过E作EF//AB交BC于F
∵DBFE是平行四边形
F
∴DE=BF
定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似
∴△ADE∽△ABC
平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.
相似
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
1、如图,DG//EH//FI//BC,请找出图中
所有的相似三角形,并说明理由。
练习
相似三角形有传递性哟!
△ADG∽ △AEH ∽ △AFI ∽ △ABC
如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
A
D
B
E
C
解: (1)
DE ∥ BC
△ADE∽△ABC
∠AED=∠C=400.
△ADE∽△ABC
在△ADE中, ∠ADE=1800-400-450=950.
练习
(2)
基础题:
1、课本:P41 A组1题、3题
2、已知:在△ABC中,EF//AB,
DF//BC,求证:△ADF∽△EFC。
作业
提高题:
如图,在△ABC中, DE//BC,并交
BA、CA的延长线于点D、E,那么
△ADE与△ABC相似吗?为什么?
相似三角形的判定(1)
河师大实验中学 张丽霞
怎样判定下面两个三角形相似?
对应角相等,对应边的比相等
F
D
E
C
A
B
∵
∴
△ABC∽△DEF
当k=1,这两个三角形有怎样的关系
课前复习
A′
B′
C′
10
6
12
51°
82°
A
6
B
C
5
3
82°
47°
6
课前复习
它们是相似三角形吗?为什么?
如图,DE//BC,且D是边AB的中点,DE交AC于E, △ADE与△ABC有什么关系 说明理由.
相似
A
B
C
D
E
证明:在△ADE与△ABC中
∠A= ∠A
∵ DE//BC
∴∠ADE=∠B, ∠AED=∠C
过E作EF//AB交BC于F
可证DBFE是平行四边形
F
△ADE≌△EFC
∴DE=BF,DE=FC
∴△ADE∽△ABC
结论:三角形的中位线截得的三角形与原三角形相似
如图,DE//BC, △ADE与△ABC有什么关系 说明理由.
相似
A
B
C
D
E
证明:在△ADE与△ABC中
∠A= ∠A
∵ DE//BC
∴∠ADE=∠B, ∠AED=∠C
过E作EF//AB交BC于F
∵DBFE是平行四边形
F
∴DE=BF
定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似
∴△ADE∽△ABC
平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.
相似
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
1、如图,DG//EH//FI//BC,请找出图中
所有的相似三角形,并说明理由。
练习
相似三角形有传递性哟!
△ADG∽ △AEH ∽ △AFI ∽ △ABC
如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
A
D
B
E
C
解: (1)
DE ∥ BC
△ADE∽△ABC
∠AED=∠C=400.
△ADE∽△ABC
在△ADE中, ∠ADE=1800-400-450=950.
练习
(2)
基础题:
1、课本:P41 A组1题、3题
2、已知:在△ABC中,EF//AB,
DF//BC,求证:△ADF∽△EFC。
作业
提高题:
如图,在△ABC中, DE//BC,并交
BA、CA的延长线于点D、E,那么
△ADE与△ABC相似吗?为什么?
