四川省南充中学2020-2021学年高二下学期入学考试数学(理)试卷 Word版含答案解析
文档属性
| 名称 | 四川省南充中学2020-2021学年高二下学期入学考试数学(理)试卷 Word版含答案解析 |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 17:22:34 | ||
图片预览




文档简介
南充高中2019级高二下期入学考试
数学试题(理科)
(时间:120分钟 总分:150分)
第Ⅰ卷(选择题 共60分)
一、单选题:本题共12小题,每小题5分,共60分.
1.( )
A. B. C. D.
2.已知,则“”是“”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
3.已知直线与直线互相平行,则实数的值为( )
A.-1 B.0 C.1 D.2
4.已知点M是△ABC的边BC的中点,点E在边AC上,且,则向量=( )
A. B.
C. D.
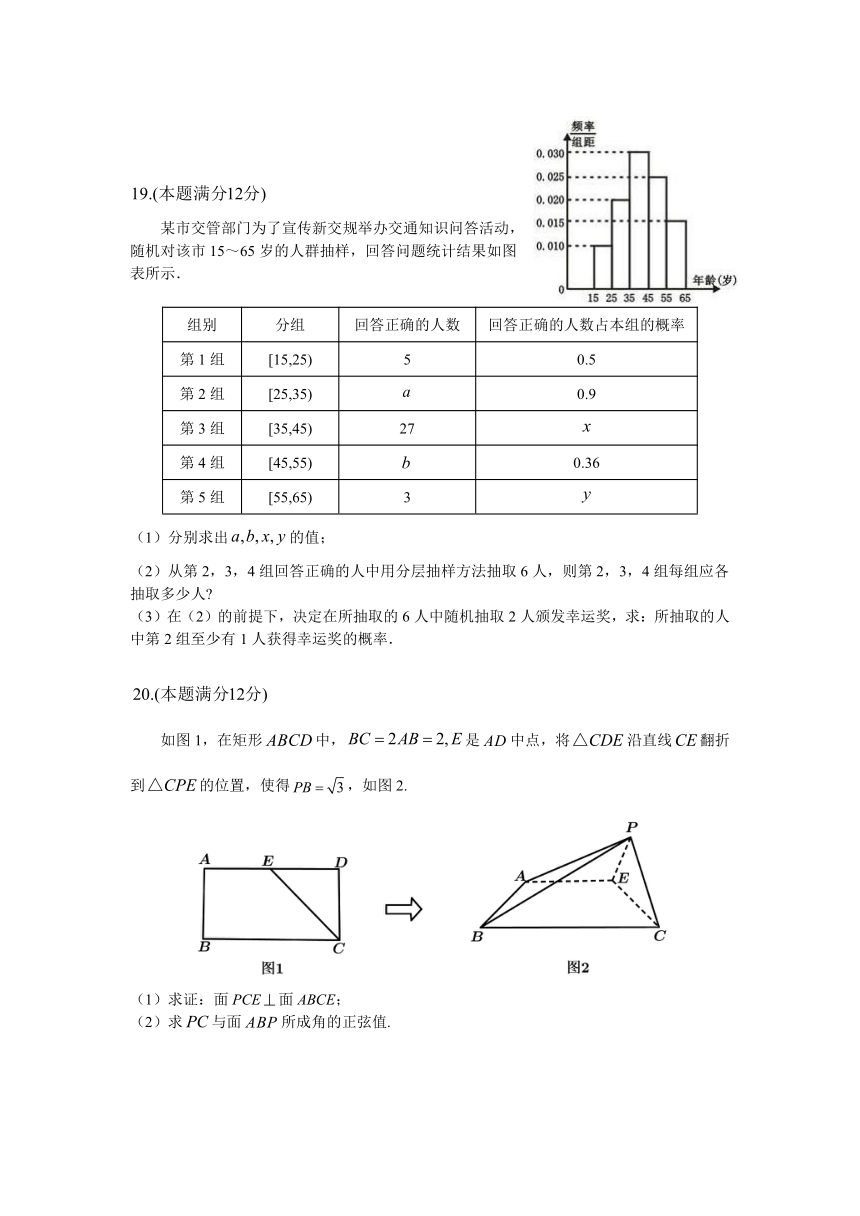
5.已知一个四棱锥的正视图、侧视图如图所示,其底面梯形的斜二测画法的直观图是一个如图
所示的等腰梯形,且该梯形的面积为,则该四棱锥的体积是( )
A.4 B. C. D.
6.设是两条不同的直线,是两个不同的平面,给出下列条件,能得到的是( )
A. B. C. D.
7. 中,若 且,则的形状是( )
A.等边三角形 B.等腰三角形 C.等腰直角三角形 D.直角三角形
8.已知直线恒过定点A,点A也在直线上,其中均为
正数,则的最小值为( )
A.2 B.4 C.6 D.8
9.已知一个几何体的三视图如图所示,俯视图为等腰三角形,
则该几何体的外接球表面积为( )
A. B.
C. D.
10.设函数,若,则的取值范围是( )
A. B.
C. D.
11.若满足约束条件,目标函数仅在点(1,0)处取得最小值,
则的取值范围是( )
A.(,) B.(,) C. D.
12.过椭圆右焦点F且斜率为的直线l交椭圆于A,B两点,M为弦AB的中点,
直线OM与椭圆相交,其中一个交点为C点,若(λ>0),则实数λ的值为( )
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题:本题共4小题,每小题5分,共20分.
13.已知,则__________.
14.已知直线与圆:相交于,两点,为坐标原点,且
,则实数的值为________.
15.分别是三棱锥的棱的中点,,,则异
面直线与所成的角为________.
16.设首项为1的数列的前n项和为,数列的前n项和为,
若,则使得成立的最小的n的值为________.
三、解答题:本题共6小题,共70分.
已知,,与夹角是.
(1)求的值及的值;
(2)当为何值时,.
已知数列的前项和为,.
(1)证明数列为等比数列并求其通项公式;
(2)若,求数列的前项和.
某市交管部门为了宣传新交规举办交通知识问答活动,
随机对该市15~65岁的人群抽样,回答问题统计结果如图
表所示.
组别 分组 回答正确的人数 回答正确的人数占本组的概率
第1组 [15,25) 5 0.5
第2组 [25,35)
0.9
第3组 [35,45) 27
第4组 [45,55)
0.36
第5组 [55,65) 3
(1)分别求出的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
如图1,在矩形中,是中点,将沿直线翻折到的位置,使得,如图2.
(1)求证:面PCE面ABCE;
(2)求与面所成角的正弦值.
设椭圆的方程为,点为坐标原点,点,的坐标分别为,,,直线的斜率为.
(1)求椭圆的方程;
(2)若斜率为的直线交椭圆于,两点,交轴于点,问是否存在实数使得以为直径的圆恒过点?若存在,求的值;若不存在,说明理由
已知三点??在圆上.为直线上的动点,与圆的另一个交点为与圆的另一个交点为.
(1)求圆的标准方程;
(2)若直线与圆相交所得弦长为,求点的坐标;
(3)证明:直线过定点.
南充高中2019级高二下期入学考试
数学参考答案(理科)
A【详解】因为,所以2.A【详解】a∈R,则“a>1”?“”,“”?“a>1或a<0”,∴“a>1”是“”的充分非必要条件.故选A.
3.B【详解】解:当时,直线:即,直线:即,满足.
当时,直线与直线互相平行,
,解得实数.综上,,故选:.
4.B【解析】由题意结合向量的加法法则可得:
A【详解】由三视图可知,该四棱锥的高是3,记斜二测画法中的等腰梯形的上底为,高为,则斜二测中等腰梯形的腰为,而积,由斜二测画法的特点知直观图中底面梯形的高为,面积
,故四棱锥的体积,故选.
(也可用结论直接得出:,,)
6.D【解析】试题分析:A.,或,或与相交,故A不成立;B:由,知或,从而不成立,故B不成立;
C:,或,或与相交,故C不成立;
D:,故D成立;故选D.
7.C【详解】由,得,
所以得,所以.所以,所以,
即,所以,所以,即,所以,,即三角形为等腰直角三角形,选.
点睛:判断三角形形状的方法
①化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.
②化角:通过三角恒等变形,得出内角的关系,从而判断三角形的形状,此时要注意应用这个结论.
8.D【解析】试题分析:变形为,所以过定点,代入直线得
,当且仅当时等号成立,取得最小值8
9.B【详解】根据三视图还原几何体如下:
设为的中点,则有,且平面,
设为的外心,为的外接圆半径,
则,故在中,有,即,
如图所示,过作,且,此时平面,
设的中点为,则,故点即为三棱锥的外接球球心,又,所以三棱锥的外接球半径,
所以三棱锥的外接球表面积,故选:B.
10.B【详解】当时,,则
当时,,,有或,则,
综上可知:的取值范围是或.故选:B.
11.B【详解】由已知可画出可行区域图,如图所示,由目标函数,而目标函数仅在可行区域顶点处取得最小值,且截距为正号,所以直线的位置可由直线绕点顺时针旋转到直线均可满足题意,而,即.故选B.
12.B【详解】设,,由题知:
,,即:.
与椭圆联立.
因为,所以.
将代入,得到:,.
,即:.与椭圆联立,解得:.
因为且,所以.故选:B
13.【详解】
又 ,本题正确结果:
14.【详解】设AB的中点为C,由题得
圆心到直线的距离为,
所以.故答案为
15.【详解】根据题意,取中点为,连接,如下图所示:
因为分别为中点,故可得//,//,
故可得即为与所成的角或其补角.
在中,.
故,故与所成的角为.故答案为:.
16.1010【详解】由题意得,,
当时,,
且当时也成立,
,
当时,,且当时也成立,
,
,,,,
使得成立的最小的n的值为1010.故答案为:1010
(1);(2)
【详解】(1)由向量的数量积的运算公式,可得,
.
(2)因为,所以,
整理得,解得.
即当值时,.
(1)证明见解析,;(2).
【详解】(1)证明:由已知可得,,令得,,
所以(),
所以当时,,整理得:,
化简得:(),
所以数列是以1为首项,3为公比的等比数列,
由等比数列的通项公式得:
(2)因为,所以,
,
则.
由错位相加法得,,
.所以
(1);(2)人,人,1人;(3).
【详解】(1)第1组人数, 所以,
第2组人数,所以,
第3组人数,所以,
第4组人数,所以,
第5组人数,所以.
(2)第2,3,4组回答正确的人的比为,所以第2,3,4组每组应各依次抽取人,人,1人.
(3)记抽取的6人中,第2组的记为,第3组的记为,第4组的记为, 则从6名幸运者中任取2名的所有可能的情况有15种,他们是:
,,,,,,,,,,,,,,.
其中第2组至少有1人的情况有9种,他们是:,,,,,,,,.故所求概率为.
20.(1)证明见解析;(2).
【详解】(1)证明:连结,
由图1可得
在图2中
又面PEC
面ABCE面PCE面ABCE
(2)以点为原点,分别以直线为轴,轴,以经过点且垂直于平面的直线为轴建立直角坐标系.
由题意可知,
设面的法向量为
则令得所以
所以直线与面所成角的正弦值为.
21.(1)(2)存在;
【详解】(1)设点的坐标为,,
,,又,,椭圆的方程为.
(2)依题意,设直线的方程为,代入,
得.
设,,则,.
假设存在实数,使得以为直径的圆恒过点,则.
又,,
∴,
即,将,代入,整理得,解得,
即当时,存在实数使得以为直径的圆恒过点.
22.(1);(2);(3)证明见解析.
【详解】解:(1)由于??
所以,故得,
点在以线段为直径的圆上,
即圆的标准方程为:;
(2)圆的半径为2,直线截圆所得弦长为,则圆心到直线的距离为.
设直线的方程为:,即.
,解得:..
则直线的方程为:,
当时,得点的坐标为;
(3)当直线斜率不存在时,设其方程为:.
取,由直线与交点的横坐标为6可得:,即此时直线的方程为:;
当直线斜率存在时,设的方程为:.
由得:.
由得:.
设,则.
且:.
直线的方程为:,直线的方程为:,
代入点的横坐标得:.
由于,故有:.
从而:,即:.
即:,
整理得:,解得或.
当时,直线为,过点,舍;
当时,直线为,过定点.综上:直线过定点.
数学试题(理科)
(时间:120分钟 总分:150分)
第Ⅰ卷(选择题 共60分)
一、单选题:本题共12小题,每小题5分,共60分.
1.( )
A. B. C. D.
2.已知,则“”是“”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
3.已知直线与直线互相平行,则实数的值为( )
A.-1 B.0 C.1 D.2
4.已知点M是△ABC的边BC的中点,点E在边AC上,且,则向量=( )
A. B.
C. D.
5.已知一个四棱锥的正视图、侧视图如图所示,其底面梯形的斜二测画法的直观图是一个如图
所示的等腰梯形,且该梯形的面积为,则该四棱锥的体积是( )
A.4 B. C. D.
6.设是两条不同的直线,是两个不同的平面,给出下列条件,能得到的是( )
A. B. C. D.
7. 中,若 且,则的形状是( )
A.等边三角形 B.等腰三角形 C.等腰直角三角形 D.直角三角形
8.已知直线恒过定点A,点A也在直线上,其中均为
正数,则的最小值为( )
A.2 B.4 C.6 D.8
9.已知一个几何体的三视图如图所示,俯视图为等腰三角形,
则该几何体的外接球表面积为( )
A. B.
C. D.
10.设函数,若,则的取值范围是( )
A. B.
C. D.
11.若满足约束条件,目标函数仅在点(1,0)处取得最小值,
则的取值范围是( )
A.(,) B.(,) C. D.
12.过椭圆右焦点F且斜率为的直线l交椭圆于A,B两点,M为弦AB的中点,
直线OM与椭圆相交,其中一个交点为C点,若(λ>0),则实数λ的值为( )
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题:本题共4小题,每小题5分,共20分.
13.已知,则__________.
14.已知直线与圆:相交于,两点,为坐标原点,且
,则实数的值为________.
15.分别是三棱锥的棱的中点,,,则异
面直线与所成的角为________.
16.设首项为1的数列的前n项和为,数列的前n项和为,
若,则使得成立的最小的n的值为________.
三、解答题:本题共6小题,共70分.
已知,,与夹角是.
(1)求的值及的值;
(2)当为何值时,.
已知数列的前项和为,.
(1)证明数列为等比数列并求其通项公式;
(2)若,求数列的前项和.
某市交管部门为了宣传新交规举办交通知识问答活动,
随机对该市15~65岁的人群抽样,回答问题统计结果如图
表所示.
组别 分组 回答正确的人数 回答正确的人数占本组的概率
第1组 [15,25) 5 0.5
第2组 [25,35)
0.9
第3组 [35,45) 27
第4组 [45,55)
0.36
第5组 [55,65) 3
(1)分别求出的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
如图1,在矩形中,是中点,将沿直线翻折到的位置,使得,如图2.
(1)求证:面PCE面ABCE;
(2)求与面所成角的正弦值.
设椭圆的方程为,点为坐标原点,点,的坐标分别为,,,直线的斜率为.
(1)求椭圆的方程;
(2)若斜率为的直线交椭圆于,两点,交轴于点,问是否存在实数使得以为直径的圆恒过点?若存在,求的值;若不存在,说明理由
已知三点??在圆上.为直线上的动点,与圆的另一个交点为与圆的另一个交点为.
(1)求圆的标准方程;
(2)若直线与圆相交所得弦长为,求点的坐标;
(3)证明:直线过定点.
南充高中2019级高二下期入学考试
数学参考答案(理科)
A【详解】因为,所以2.A【详解】a∈R,则“a>1”?“”,“”?“a>1或a<0”,∴“a>1”是“”的充分非必要条件.故选A.
3.B【详解】解:当时,直线:即,直线:即,满足.
当时,直线与直线互相平行,
,解得实数.综上,,故选:.
4.B【解析】由题意结合向量的加法法则可得:
A【详解】由三视图可知,该四棱锥的高是3,记斜二测画法中的等腰梯形的上底为,高为,则斜二测中等腰梯形的腰为,而积,由斜二测画法的特点知直观图中底面梯形的高为,面积
,故四棱锥的体积,故选.
(也可用结论直接得出:,,)
6.D【解析】试题分析:A.,或,或与相交,故A不成立;B:由,知或,从而不成立,故B不成立;
C:,或,或与相交,故C不成立;
D:,故D成立;故选D.
7.C【详解】由,得,
所以得,所以.所以,所以,
即,所以,所以,即,所以,,即三角形为等腰直角三角形,选.
点睛:判断三角形形状的方法
①化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.
②化角:通过三角恒等变形,得出内角的关系,从而判断三角形的形状,此时要注意应用这个结论.
8.D【解析】试题分析:变形为,所以过定点,代入直线得
,当且仅当时等号成立,取得最小值8
9.B【详解】根据三视图还原几何体如下:
设为的中点,则有,且平面,
设为的外心,为的外接圆半径,
则,故在中,有,即,
如图所示,过作,且,此时平面,
设的中点为,则,故点即为三棱锥的外接球球心,又,所以三棱锥的外接球半径,
所以三棱锥的外接球表面积,故选:B.
10.B【详解】当时,,则
当时,,,有或,则,
综上可知:的取值范围是或.故选:B.
11.B【详解】由已知可画出可行区域图,如图所示,由目标函数,而目标函数仅在可行区域顶点处取得最小值,且截距为正号,所以直线的位置可由直线绕点顺时针旋转到直线均可满足题意,而,即.故选B.
12.B【详解】设,,由题知:
,,即:.
与椭圆联立.
因为,所以.
将代入,得到:,.
,即:.与椭圆联立,解得:.
因为且,所以.故选:B
13.【详解】
又 ,本题正确结果:
14.【详解】设AB的中点为C,由题得
圆心到直线的距离为,
所以.故答案为
15.【详解】根据题意,取中点为,连接,如下图所示:
因为分别为中点,故可得//,//,
故可得即为与所成的角或其补角.
在中,.
故,故与所成的角为.故答案为:.
16.1010【详解】由题意得,,
当时,,
且当时也成立,
,
当时,,且当时也成立,
,
,,,,
使得成立的最小的n的值为1010.故答案为:1010
(1);(2)
【详解】(1)由向量的数量积的运算公式,可得,
.
(2)因为,所以,
整理得,解得.
即当值时,.
(1)证明见解析,;(2).
【详解】(1)证明:由已知可得,,令得,,
所以(),
所以当时,,整理得:,
化简得:(),
所以数列是以1为首项,3为公比的等比数列,
由等比数列的通项公式得:
(2)因为,所以,
,
则.
由错位相加法得,,
.所以
(1);(2)人,人,1人;(3).
【详解】(1)第1组人数, 所以,
第2组人数,所以,
第3组人数,所以,
第4组人数,所以,
第5组人数,所以.
(2)第2,3,4组回答正确的人的比为,所以第2,3,4组每组应各依次抽取人,人,1人.
(3)记抽取的6人中,第2组的记为,第3组的记为,第4组的记为, 则从6名幸运者中任取2名的所有可能的情况有15种,他们是:
,,,,,,,,,,,,,,.
其中第2组至少有1人的情况有9种,他们是:,,,,,,,,.故所求概率为.
20.(1)证明见解析;(2).
【详解】(1)证明:连结,
由图1可得
在图2中
又面PEC
面ABCE面PCE面ABCE
(2)以点为原点,分别以直线为轴,轴,以经过点且垂直于平面的直线为轴建立直角坐标系.
由题意可知,
设面的法向量为
则令得所以
所以直线与面所成角的正弦值为.
21.(1)(2)存在;
【详解】(1)设点的坐标为,,
,,又,,椭圆的方程为.
(2)依题意,设直线的方程为,代入,
得.
设,,则,.
假设存在实数,使得以为直径的圆恒过点,则.
又,,
∴,
即,将,代入,整理得,解得,
即当时,存在实数使得以为直径的圆恒过点.
22.(1);(2);(3)证明见解析.
【详解】解:(1)由于??
所以,故得,
点在以线段为直径的圆上,
即圆的标准方程为:;
(2)圆的半径为2,直线截圆所得弦长为,则圆心到直线的距离为.
设直线的方程为:,即.
,解得:..
则直线的方程为:,
当时,得点的坐标为;
(3)当直线斜率不存在时,设其方程为:.
取,由直线与交点的横坐标为6可得:,即此时直线的方程为:;
当直线斜率存在时,设的方程为:.
由得:.
由得:.
设,则.
且:.
直线的方程为:,直线的方程为:,
代入点的横坐标得:.
由于,故有:.
从而:,即:.
即:,
整理得:,解得或.
当时,直线为,过点,舍;
当时,直线为,过定点.综上:直线过定点.
同课章节目录
