5.3.2 函数的极值(22张PPT)
文档属性
| 名称 | 5.3.2 函数的极值(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 19:34:26 | ||
图片预览





文档简介
5.3.2 函数的极值
人教A版(2019)
选择性必修第二册
新知导入
新知导入
题西林壁
宋?苏轼
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
新知讲解
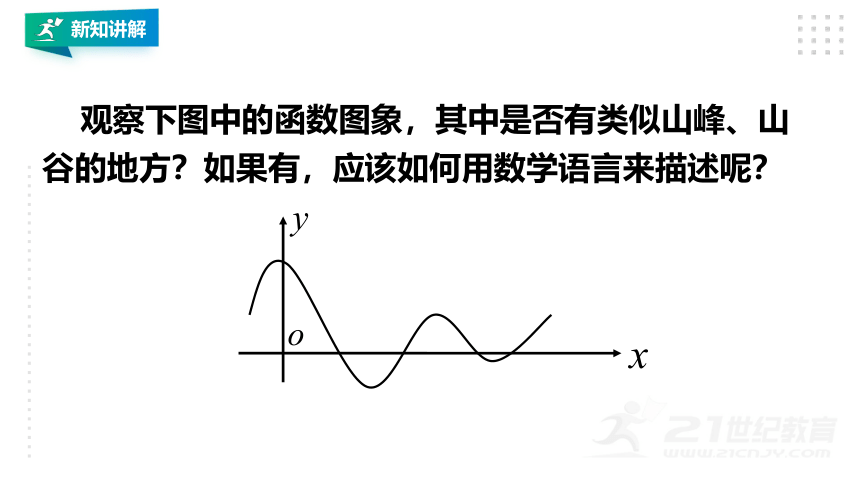
观察下图中的函数图象,其中是否有类似山峰、山谷的地方?如果有,应该如何用数学语言来描述呢?
1.了解极大值、极小值的概念.(难点)
2.了解函数在某点取得极值的必要条件和充分条件.(重点、易混点)
3.会用导数求函数的极大值、极小值.(重点)
学习目标
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
1、函数y=f(x)的单调性与导数f ′(x)的正负之间的关系?
2、判断函数y=f(x)的单调性的步骤?
复习回顾
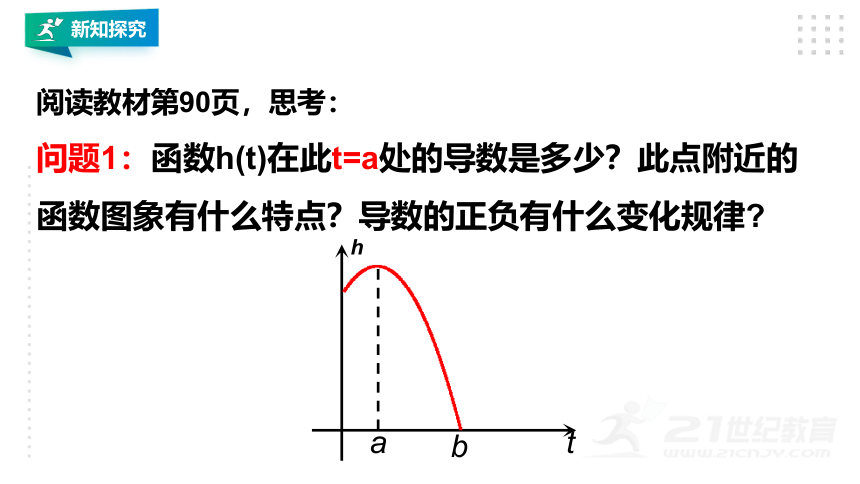
阅读教材第90页,思考:
问题1:函数h(t)在此t=a处的导数是多少?此点附近的函数图象有什么特点?导数的正负有什么变化规律?
t
a
b
h
新知探究
单调递增
单调递减
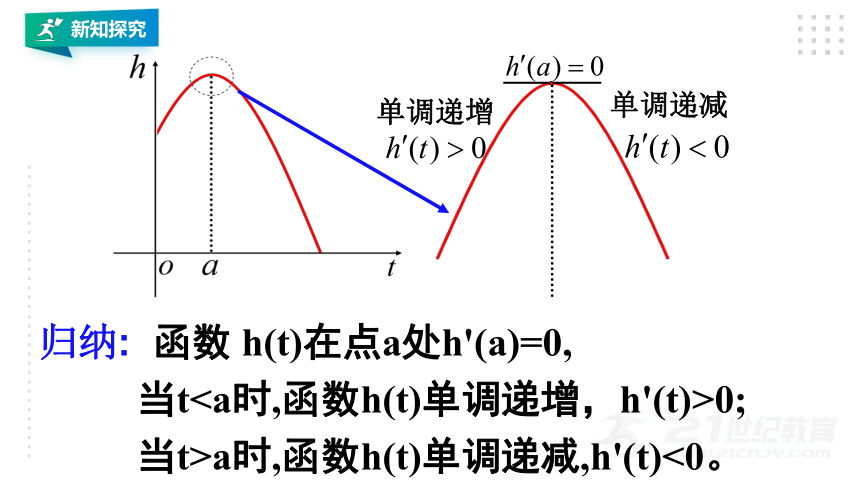
归纳: 函数 h(t)在点a处h'(a)=0,
当t0;
当t>a时,函数h(t)单调递减,h'(t)<0。
新知探究
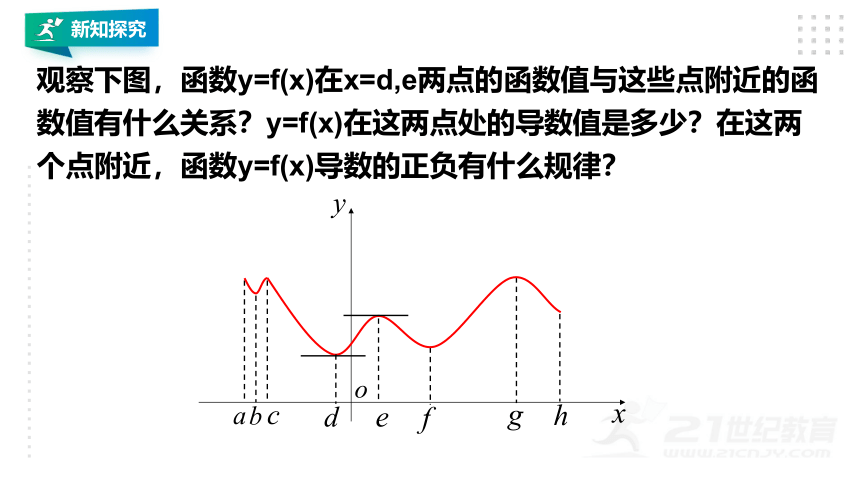
观察下图,函数y=f(x)在x=d,e两点的函数值与这些点附近的函数值有什么关系?y=f(x)在这两点处的导数值是多少?在这两个点附近,函数y=f(x)导数的正负有什么规律?
新知探究
函数y=f(x)在点x=d的函数值f(d)比在其附近其他点的函数值都小,
f '(d)=0.
在点x=d 附近的左侧 f '(x) <0
在点x=d 附近的右侧 f '(x)>0
函数y=f(x)在点x=e的函数值f(e)比在其附近其他点的函数值都小,
f '(e)=0.
在点x=e附近的左侧 f '(x) <0
在点x=e 附近的右侧 f '(x)>0
点d叫做函数y=f(x)的极小值点,
f(d)叫做函数y=f(x)的极小值.
点e叫做函数y=f(x)的极大值点,
f(e)叫做函数y=f(x)的极大值.
新知探究
思考:极大值一定大于极小值吗?
极小值点、极大值点统称极值点,极大值和极小值统称为极值.
极小值
极大值
总结归纳
注意:
(1)极值是一个局部概念。
(2)函数的极值不是唯一的。即一个函数在某区间上或定义域内极大值或极小值可以不止一个。
(3)极大值与极小值之间无确定的大小关系。即一个函数的极大值未必大于极小值。
(4)函数的极值点是实数,不是一个点;它一定出现在区间的内部,区间的端点不可能成为极值点。
归纳总结
例1 如图是函数y=f(x)的图象,试找出函数y=f(x)的极值点,并指出哪些是极大值点,哪些是极小值点?
变式练习:
如果把函数图象改为导函数y=f'(x)的图象?
+
-
+
+
极大值点x2
极小值点x4
不是极值点
思考:导数值为0的点一定是函数的极值点吗?
新知讲解
o
a
x0
b
x
y
x
x0左侧
x0
x0右侧
f?(x)
f(x)
o
a
x0
b
x
y
x
x0左侧
x0
x0右侧
f?(x)
f(x)
增
+
f?(x) =0
-
极大值
减
-
f?(x) =0
增
减
极小值
+
左正右负为极大,
左负右正为极小
1、
2、
f?(x0) =0 x0 是可导函数f(x)的极值点
?
必要不充分
即:f /(x0)=0是函数取得极值的 条件
方法归纳
新知讲解
求可导函数f(x)极值的步骤:
(1) 确定函数的定义域;
(2)求导数f '(x)的零点;
(3)把定义域划分为部分区间,并列成表格,根据导数与极值的关系求解。
方法归纳
例3 已知函数 在 处取得极值。
(1)求函数 的解析式
(2)求函数 的单调区间
新知讲解
已知函数极值,确定函数解析式中的参数时:
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解.
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.
方法归纳
2.函数 的定义域为区间 导函数 在
内的图像如图所示,则函数 在开区间 内有( )个极小值点。
1.函数f(x)=x3+3ax2+3(a+2)x+3既有极大值,又有极小值,则a的取值范围为 .
(A)1 (B)2 (C)3 (D) 4
课堂练习
如果在x0附近的左侧f '(x)>0,右侧f '(x)<0 ,那么 f (x0) 为极大值;
解方程 f '(x) = 0.当 f '(x0) = 0 时:
如果在x0附近的左侧f '(x)<0,右侧f '(x)>0 ,那么 f (x0) 为极小值;
3.求函数 y=f(x)的极值的一般方法:
一般地,设函数f(x)在a附近有定义,如果对a附近的所有的点,都有f(x)>f(a),
f(a)是函数y=f(x)的极小值,a是极小值点.
设函数f(x)在点b附近有定义,如果对b附近的所有的点,都有f(x)<f(b),
f(b)是函数y=f(x)的极大值,b 是极大值点.极小值点、极大值点统称为极值点,极小值、极大值统称为极值。
2.极值点两侧导数正负符号的规律:极值点两侧,导数正负符号相异
1.函数的极大值和极小值的概念:
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教A版(2019)
选择性必修第二册
新知导入
新知导入
题西林壁
宋?苏轼
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
新知讲解
观察下图中的函数图象,其中是否有类似山峰、山谷的地方?如果有,应该如何用数学语言来描述呢?
1.了解极大值、极小值的概念.(难点)
2.了解函数在某点取得极值的必要条件和充分条件.(重点、易混点)
3.会用导数求函数的极大值、极小值.(重点)
学习目标
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
1、函数y=f(x)的单调性与导数f ′(x)的正负之间的关系?
2、判断函数y=f(x)的单调性的步骤?
复习回顾
阅读教材第90页,思考:
问题1:函数h(t)在此t=a处的导数是多少?此点附近的函数图象有什么特点?导数的正负有什么变化规律?
t
a
b
h
新知探究
单调递增
单调递减
归纳: 函数 h(t)在点a处h'(a)=0,
当t
当t>a时,函数h(t)单调递减,h'(t)<0。
新知探究
观察下图,函数y=f(x)在x=d,e两点的函数值与这些点附近的函数值有什么关系?y=f(x)在这两点处的导数值是多少?在这两个点附近,函数y=f(x)导数的正负有什么规律?
新知探究
函数y=f(x)在点x=d的函数值f(d)比在其附近其他点的函数值都小,
f '(d)=0.
在点x=d 附近的左侧 f '(x) <0
在点x=d 附近的右侧 f '(x)>0
函数y=f(x)在点x=e的函数值f(e)比在其附近其他点的函数值都小,
f '(e)=0.
在点x=e附近的左侧 f '(x) <0
在点x=e 附近的右侧 f '(x)>0
点d叫做函数y=f(x)的极小值点,
f(d)叫做函数y=f(x)的极小值.
点e叫做函数y=f(x)的极大值点,
f(e)叫做函数y=f(x)的极大值.
新知探究
思考:极大值一定大于极小值吗?
极小值点、极大值点统称极值点,极大值和极小值统称为极值.
极小值
极大值
总结归纳
注意:
(1)极值是一个局部概念。
(2)函数的极值不是唯一的。即一个函数在某区间上或定义域内极大值或极小值可以不止一个。
(3)极大值与极小值之间无确定的大小关系。即一个函数的极大值未必大于极小值。
(4)函数的极值点是实数,不是一个点;它一定出现在区间的内部,区间的端点不可能成为极值点。
归纳总结
例1 如图是函数y=f(x)的图象,试找出函数y=f(x)的极值点,并指出哪些是极大值点,哪些是极小值点?
变式练习:
如果把函数图象改为导函数y=f'(x)的图象?
+
-
+
+
极大值点x2
极小值点x4
不是极值点
思考:导数值为0的点一定是函数的极值点吗?
新知讲解
o
a
x0
b
x
y
x
x0左侧
x0
x0右侧
f?(x)
f(x)
o
a
x0
b
x
y
x
x0左侧
x0
x0右侧
f?(x)
f(x)
增
+
f?(x) =0
-
极大值
减
-
f?(x) =0
增
减
极小值
+
左正右负为极大,
左负右正为极小
1、
2、
f?(x0) =0 x0 是可导函数f(x)的极值点
?
必要不充分
即:f /(x0)=0是函数取得极值的 条件
方法归纳
新知讲解
求可导函数f(x)极值的步骤:
(1) 确定函数的定义域;
(2)求导数f '(x)的零点;
(3)把定义域划分为部分区间,并列成表格,根据导数与极值的关系求解。
方法归纳
例3 已知函数 在 处取得极值。
(1)求函数 的解析式
(2)求函数 的单调区间
新知讲解
已知函数极值,确定函数解析式中的参数时:
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解.
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.
方法归纳
2.函数 的定义域为区间 导函数 在
内的图像如图所示,则函数 在开区间 内有( )个极小值点。
1.函数f(x)=x3+3ax2+3(a+2)x+3既有极大值,又有极小值,则a的取值范围为 .
(A)1 (B)2 (C)3 (D) 4
课堂练习
如果在x0附近的左侧f '(x)>0,右侧f '(x)<0 ,那么 f (x0) 为极大值;
解方程 f '(x) = 0.当 f '(x0) = 0 时:
如果在x0附近的左侧f '(x)<0,右侧f '(x)>0 ,那么 f (x0) 为极小值;
3.求函数 y=f(x)的极值的一般方法:
一般地,设函数f(x)在a附近有定义,如果对a附近的所有的点,都有f(x)>f(a),
f(a)是函数y=f(x)的极小值,a是极小值点.
设函数f(x)在点b附近有定义,如果对b附近的所有的点,都有f(x)<f(b),
f(b)是函数y=f(x)的极大值,b 是极大值点.极小值点、极大值点统称为极值点,极小值、极大值统称为极值。
2.极值点两侧导数正负符号的规律:极值点两侧,导数正负符号相异
1.函数的极大值和极小值的概念:
课堂小结
https://www.21cnjy.com/help/help_extract.php
