带电粒子在电场中的运动
图片预览





文档简介
(共13张PPT)
复习:
1.计算电场力做功的方法。
W电= -ΔEP
W电=Uq
W电=FLcosθ
适用于匀强电场
适用于一切电场
2.判断粒子的运动
F合与v0在一条直线上,
F合与v0不在一条直线上,
做直线运动
做曲线运动
3、某些带电体是否考虑重力,要根据题目暗示或运动状态来判定
电场中的带电粒子一般可分为两类:
1、带电的基本粒子:如电子,质子,α粒子,正负离子等。这些粒子所受重力和电场力相比在小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2、带电微粒:如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
一、不计重力,带电粒子平行电场方向进入匀强电场中
正电荷:
匀加速直线运动
负电荷:
匀减速直线运动
+
-
qE
qE
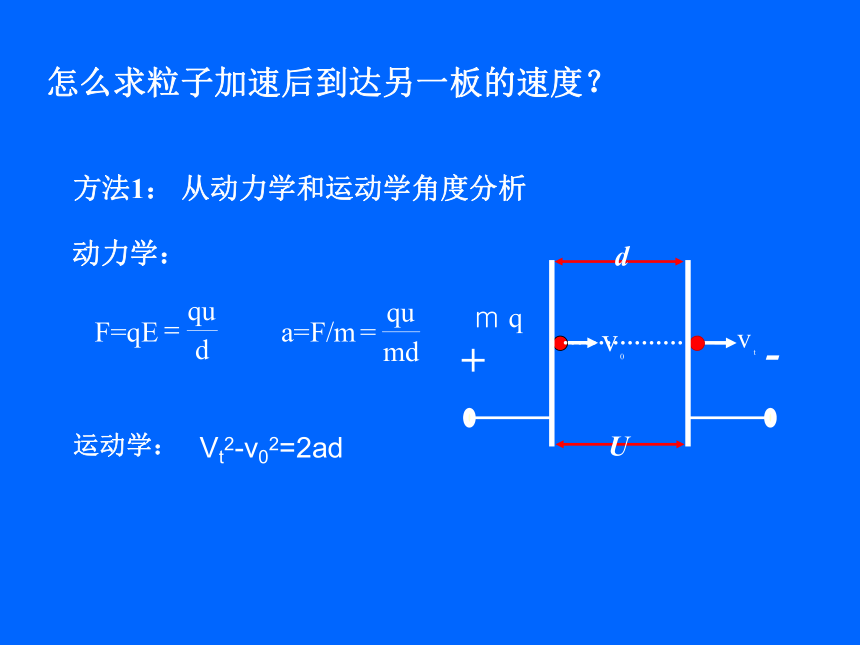
方法1:
从动力学和运动学角度分析
动力学:
F=qE
a=F/m
运动学:
=
U
+
-
m q
d
Vt2-v02=2ad
怎么求粒子加速后到达另一板的速度?
方法2:
从做功和能量的角度分析
粒子只受到电场力做功
=0
问题:如果不是匀强电场,上面公式是否适用?
U
+
-
d
q
≠
0
二、不计重力,初速度垂直于电场方向飞入匀强电场
处理方法:
1)粒子在与电场垂直的方向上做
匀速直线运动
2)粒子在与电场平行的方向上做
初速度为零的匀加速运动
类似平抛运动的分析方法
l
+
+
+
+
+
+
-
-
-
-
-
-
-q
v
v0
vy
y
d
U
vx
v0
X=
v0
t
t=
=
vy
=
at
y=
=
=
=
v0
F
=
=
=
=
α
α
=
tan
α
l
__
v0
y=
tan
α
例题:离子发生器发射出一束质量为m,电荷量为q的负离子,从静止
经加速电压 加速后,获得速度 ,并沿垂直于电场线方向
射入两平行板中央,受偏转电压 作用后,以速度V离开电
场,已知平行板长为L,两板间距离为d,
1)离子在偏转电场中运动
的时间、加速度、速度
V的大小;
2)离子在离开偏转电场时
的横向偏移量和偏转角
的正切值。
l
+
+
+
+
+
+
-
-
-
-
-
-
u1
d
v0
求:
解:
l
+
+
+
+
+
+
-
-
-
-
-
-
-q
v0
F
u1
vy
v0
由动能定理得到
即
=
v0
1)离子在偏转电场中运动的时间、加速度、速度V的大小
t=
=
加速度
a=
速度V的大小
vy
=at
˙
v
时间
V
2)离子在离开偏转电场时的横向偏移量和偏转角的正切值。
l
+
+
+
+
+
+
-
-
-
-
-
-
-q
y
v0
F
α
α
u1
vy
v0
横向偏移量
解:
a
t=
˙
偏转角的正切值:
tan
α
=
˙
v0
=
vy
和带电粒子q、m无关,只取决于加速电场和偏转电场
和带电粒子q、m无关,只取决于加速电场和偏转电场
思考题:让一价氢离子、一价氦离子和二价氦离子的混合物经过
同一加速电场由静止开始加速,然后在同一偏转电场里
偏转,它们是否会分为三股?请说明理由。
比较离子在偏转电场的侧移距离y
如果 y不相同
比较离子是否以相同偏角φ 射出
如果 y 相同
如果φ不相同
会分为三股
如果φ 相同
不会分为三股
会分为三股
课堂小结:
一、利用电场使带电粒子加速
二、利用电场使带电粒子偏转
从动力学和运动学角度分析
从做功和能量的角度分析
类似平抛运动的分析方法
粒子在与电场垂直的方向上做
匀速直线运动
粒子在与电场平行的方向上做
初速度为零的匀加速运动
复习:
1.计算电场力做功的方法。
W电= -ΔEP
W电=Uq
W电=FLcosθ
适用于匀强电场
适用于一切电场
2.判断粒子的运动
F合与v0在一条直线上,
F合与v0不在一条直线上,
做直线运动
做曲线运动
3、某些带电体是否考虑重力,要根据题目暗示或运动状态来判定
电场中的带电粒子一般可分为两类:
1、带电的基本粒子:如电子,质子,α粒子,正负离子等。这些粒子所受重力和电场力相比在小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2、带电微粒:如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
一、不计重力,带电粒子平行电场方向进入匀强电场中
正电荷:
匀加速直线运动
负电荷:
匀减速直线运动
+
-
qE
qE
方法1:
从动力学和运动学角度分析
动力学:
F=qE
a=F/m
运动学:
=
U
+
-
m q
d
Vt2-v02=2ad
怎么求粒子加速后到达另一板的速度?
方法2:
从做功和能量的角度分析
粒子只受到电场力做功
=0
问题:如果不是匀强电场,上面公式是否适用?
U
+
-
d
q
≠
0
二、不计重力,初速度垂直于电场方向飞入匀强电场
处理方法:
1)粒子在与电场垂直的方向上做
匀速直线运动
2)粒子在与电场平行的方向上做
初速度为零的匀加速运动
类似平抛运动的分析方法
l
+
+
+
+
+
+
-
-
-
-
-
-
-q
v
v0
vy
y
d
U
vx
v0
X=
v0
t
t=
=
vy
=
at
y=
=
=
=
v0
F
=
=
=
=
α
α
=
tan
α
l
__
v0
y=
tan
α
例题:离子发生器发射出一束质量为m,电荷量为q的负离子,从静止
经加速电压 加速后,获得速度 ,并沿垂直于电场线方向
射入两平行板中央,受偏转电压 作用后,以速度V离开电
场,已知平行板长为L,两板间距离为d,
1)离子在偏转电场中运动
的时间、加速度、速度
V的大小;
2)离子在离开偏转电场时
的横向偏移量和偏转角
的正切值。
l
+
+
+
+
+
+
-
-
-
-
-
-
u1
d
v0
求:
解:
l
+
+
+
+
+
+
-
-
-
-
-
-
-q
v0
F
u1
vy
v0
由动能定理得到
即
=
v0
1)离子在偏转电场中运动的时间、加速度、速度V的大小
t=
=
加速度
a=
速度V的大小
vy
=at
˙
v
时间
V
2)离子在离开偏转电场时的横向偏移量和偏转角的正切值。
l
+
+
+
+
+
+
-
-
-
-
-
-
-q
y
v0
F
α
α
u1
vy
v0
横向偏移量
解:
a
t=
˙
偏转角的正切值:
tan
α
=
˙
v0
=
vy
和带电粒子q、m无关,只取决于加速电场和偏转电场
和带电粒子q、m无关,只取决于加速电场和偏转电场
思考题:让一价氢离子、一价氦离子和二价氦离子的混合物经过
同一加速电场由静止开始加速,然后在同一偏转电场里
偏转,它们是否会分为三股?请说明理由。
比较离子在偏转电场的侧移距离y
如果 y不相同
比较离子是否以相同偏角φ 射出
如果 y 相同
如果φ不相同
会分为三股
如果φ 相同
不会分为三股
会分为三股
课堂小结:
一、利用电场使带电粒子加速
二、利用电场使带电粒子偏转
从动力学和运动学角度分析
从做功和能量的角度分析
类似平抛运动的分析方法
粒子在与电场垂直的方向上做
匀速直线运动
粒子在与电场平行的方向上做
初速度为零的匀加速运动
