第九章 9.2.1 总体取值规律的估计(共20张PPT)2020-2021学年高一数学人教A版(2019)必修第二册
文档属性
| 名称 | 第九章 9.2.1 总体取值规律的估计(共20张PPT)2020-2021学年高一数学人教A版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 22:32:22 | ||
图片预览











文档简介
第九章 §9.2 用样本估计总体
9.2.1 总体取值规律的估计
学习目标
XUE XI MU BIAO
1.掌握频率分布表的作法以及频率分布直方图的画法.
2.掌握用频率分布直方图估计总体.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 频率分布直方图
作频率分布直方图的步骤
(1)求极差:极差为一组数据中最大值与最小值的 .
(2)决定组距与组数
将数据分组时,一般取 组距,并且组距应力求“取整”,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.
(3)将数据分组
差
等长
高度
思考 要做频率分布表,需要对原始数据做哪些工作?
答案 分组,频数累计,计算频数和频率.
知识点二 其它统计图表
统计图表
主要应用
扇形图
直观描述各类数据占 的比例
条形图和直方图
直观描述不同类别或分组数据的___________
折线图
描述 随时间的变化趋势
总数
频数和频率
数据
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.频率分布直方图中小长方形的高表示该组上的个体在样本中出现的频率与组距的比值.( )
2.频率分布直方图中小长方形的面积表示该组的个体数.( )
3.频率分布直方图中所有小长方形面积之和为1.( )
4.样本容量越大,用样本的频率分布去估计总体的频率分布就越准确.
( )
√
×
√
√
2
题型探究
PART TWO
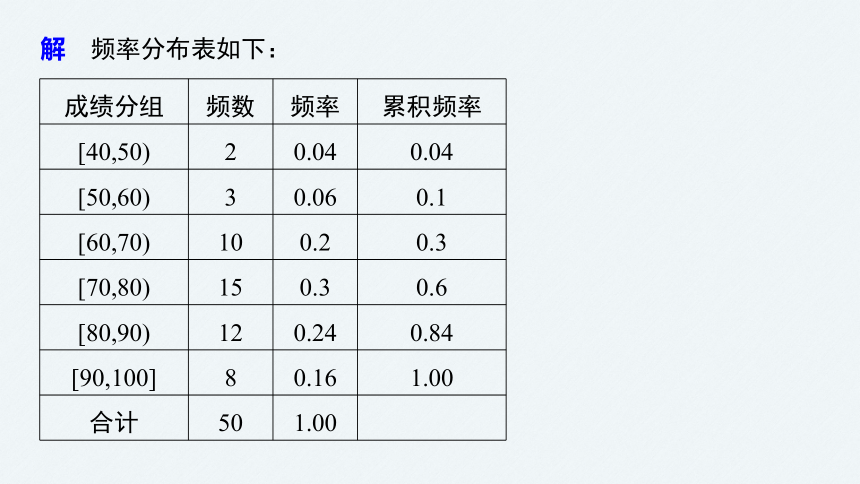
例1 从某校高三学生中抽取50名参加数学竞赛,成绩分组(单位:分)及各组的频数如下:
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表(含累积频率);
一、画频率分布直方图
解 频率分布表如下:
成绩分组
频数
频率
累积频率
[40,50)
2
0.04
0.04
[50,60)
3
0.06
0.1
[60,70)
10
0.2
0.3
[70,80)
15
0.3
0.6
[80,90)
12
0.24
0.84
[90,100]
8
0.16
1.00
合计
50
1.00
?
(2)画出频率分布直方图;
解 频率分布直方图如图所示.
(3)估计成绩在[60,90)分的学生比例.
解 学生成绩在[60,90)分的频率为0.2+0.3+0.24=0.74=74%,
所以估计成绩在[60,90)分的学生比例为74%.
反思感悟
绘制频率分布直方图的注意点
(1)各组频率的和等于1,因此,各小矩形的面积之和也等于1.
(3)同样一组数据,如果组距不同,横轴、纵轴单位不同,得到的频率分布直方图的形状也会不同.
跟踪训练1 为了了解九年级学生中女生的身高(单位:cm)情况,某中学对九年级部分女生身高进行了一次测量,所得数据整理后列出的频率分布表如右:
(1)求出表中m,n,M,N所表示的数分别是多少;
分组
频数
频率
[145.5,149.5)
1
0.02
[149.5,153.5)
4
0.08
[153.5,157.5)
20
0.40
[157.5,161.5)
15
0.30
[161.5,165.5)
8
0.16
[165.5,169.5]
m
n
合计
M
N
∴m=2,M=1+4+20+15+8+2=50.
(2)画出频率分布直方图;
解 作出直角坐标系,组距为4,纵轴表示 ,横轴表示身高,画出频率分布直方图如图所示.
(3)全体女生中身高在哪组范围内的人数最多?估计九年级学生中女生的身高在161.5 cm以上的频率.
解 由频率分布直方图可知,样本中身高在[153.5,157.5)范围内的人数最多,且身高在161.5 cm以上的频率为0.16+0.04=0.20,由此可估计全体女生中身高在[153.5,157.5)范围内的人数最多,九年级学生中女生的身高在161.5 cm以上的频率为0.20.
二、频率分布直方图的应用
例2 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?
样本容量是多少?
解 频率分布直方图是以面积的形式来反映数据落在各小组内的频率大小的,
(2)若次数在110以上(含110次)为达标,则该校高一年级全体学生的达标率约是多少?
反思感悟
(1)频率分布直方图的性质
①因为小矩形的面积=组距× =频率,所以各小矩形的
面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小组内的频率大小.
②在频率分布直方图中,各小矩形的面积之和等于1.
③ =样本容量.
(2)频率分布直方图反映了样本在各个范围内取值的可能性,由抽样的代表性利用样本在某一范围内的频率,可近似地估计总体在这一范围内的可能性.
跟踪训练2 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100?
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的比例;
解 根据频数分布表知,100名学生中一周课外阅读时间不少于12小时的学生共有6+2+2=10(名),
所以样本中的学生一周课外阅读时间少于12小时的频率是1- =0.9.
故从该校随机选取一名学生,估计其该周课外阅读时间少于12小时的比例为0.9.
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100?
(2)求频率分布直方图中a,b的值;
课外阅读时间落在[8,10)组内的有25人,频率为0.25,
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论).
解 样本中的100名学生该周课外阅读时间的平均数在第4组.
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100?
三、折线图、条形图、扇形图及应用
例3 如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计图和条形统计图.
解 该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期
1
2
3
4
5
6
7
8
9
10
最低气温(℃)
-3
-2
0
-1
1
2
0
-1
2
2
其中最低气温为-3 ℃的有1天,占10%,最低气温为-2 ℃的有1天,占10%,最低气温为-1 ℃的有2天,占20%,最低气温为0 ℃的有2天,占20%,最低气温为1 ℃的有1天,占10%,最低气温为2 ℃的有3天,占30%,扇形统计图如图所示.
条形统计图如图所示:
反思感悟
(1)条形图是用一个单位长度表示一定的数量或频率,根据数量的多少或频率的大小画成长短不同的矩形条,条形图能清楚地表示出每个项目的具体数目或频率.
(2)扇形图是用整个圆面积表示总数(100%),用圆内的扇形面积表示各个部分所占总数的百分数.
(3)在画折线图时,要注意明确横轴、纵轴的实际含义.
跟踪训练3 华为、抖音海外版事件暴露了我国计算机行业中芯片、软件两大短板,为防止“卡脖子”事件的再次发生,科技专业人才就成了决胜的关键.为了解我国在芯片、软件方面的潜力,某调查机构对我国若干大型科技公司进行调查统计,得到了这两个行业从业者的年龄分布的饼形图和“90后”从事这两个行业的岗位分布雷达图,
则下列说法中不一定正确的是
A.芯片、软件行业从业者中,“90后”占总人数的比例超过50%
B.芯片、软件行业中从事技术、设计岗位的“90后”人数超过总人数
的25%
C.芯片、软件行业从事技术岗位的人中,“90后”比“80后”多
D.芯片、软件行业中,“90后”从事市场岗位的人数比“80前”的总
人数多
√
解析 对于选项A,芯片、软件行业从业者中“90后”占总人数的55%,故选项A正确;
对于选项B,芯片、软件行业中从事技术、设计岗位的“90后”占总人数的(37%+13%)×55%=27.5%,故选项B正确;
对于选项C,芯片、软件行业中从事技术岗位的“90后”占总人数的37%×55%=20.35%,“80后”占总人数的40%,但从事技术的“80后”占总人数的百分比不知道,无法确定二者人数多少,故选项C错误;
对于选项D,芯片、软件行业中从事市场岗位的“90后”占总人数的14%×55%=7.7%,“80前”占总人数的5%,故选项D正确.
3
随堂演练
PART THREE
1
2
3
4
5
1.用样本频率分布估计总体频率分布的过程中,下列说法正确的是
A.总体容量越大,估计越精确
B.总体容量越小,估计越精确
C.样本容量越大,估计越精确
D.样本容量越小,估计越精确
√
解析 用样本的频率分布估计总体的频率分布时,在总体一定时,样本的容量越大,估计就越精确.
2.一个容量为20的样本数据,分组与频数如下表:
分组
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
[60,70]
频数
2
3
4
5
4
2
则样本在[10,50)内的频率为
A.0.5 B.0.24 C.0.6 D.0.7
√
解析 因为样本在[10,50)内的频数为2+3+4+5=14,样本容量为20,
1
2
3
4
5
3.(多选)容量为100的样本,其数据分布在[2,18]内,将样本数据分为4组:[2,6),[6,10),[10,14),[14,18],得到频率分布直方图如图所示,则下列说法中正确的是
A.样本数据分布在[6,10)内的频率为0.32
B.样本数据分布在[10,14)内的频数为40
C.样本数据分布在[2,10)内的频数为40
D.估计总体数据大约有10%分布在[10,14)内
√
√
√
1
2
3
4
5
1
2
3
4
5
对于C,由题图可得,样本数据分布在[2,10)内的频数为100×(0.02+0.08)×4=40,所以C正确.
对于D,由题图可估计,总体数据分布在[10,14)内的比例为0.1×4=0.4=40%,所以D错误,故选ABC.
解析 对于A,由题图可得,样本数据分布在[6,10)内的频率为0.08×4=0.32,所以A正确.
对于B,由题图可得,样本数据分布在[10,14)内的频数为100×(0.1×4)=40,所以B正确.
4.某地政府调查了工薪阶层1 000人的月工资,并根据调查结果画出如图所示的频率分布直方图,为了了解工薪阶层对月工资的满意程度,要用分层随机抽样的方法从调查的1 000人中抽出100人做电话询访,则月工资在区间[30,35)内的工薪阶层应抽出_____人.
15
解析 月工资落在区间[30,35)内的频率为1-(0.02+0.04+0.05+0.05+0.01)×5=0.15,
所以月工资在区间[30,35)内的工薪阶层应抽出100×0.15=15(人).
1
2
3
4
5
5.为了解今年某校高三毕业班准备报考飞行员学生的体重(单位:千克)情况,将所得的数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前三个小组的频率之比为1∶2∶3,其中第2小组的频数为12.则该校报考飞行员的总人数为_____.
48
1
2
3
4
5
解析 设报考飞行员的总人数为n,
设第1小组的频率为a,
则有a+2a+3a+(0.013+0.037)×5=1,
解得a=0.125,
所以第2小组的频率为0.25.
又第2小组的频数为12,
1
2
3
4
5
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)频数与频率.
(2)频率分布表.
(3)频率分布直方图.
(4)扇形图、条形图和折线图.
2.方法归纳:图表识别、数据分析.
3.常见误区:频率分布直方图中小矩形的高以及小矩形的面积代表的意义理解不清.
4
课时对点练
PART FOUR
基础巩固
1.从一堆苹果中任取10个,称得它们的质量如下(单位:克):125 120 122 105 130 114 116 95 120 134
则样本数据落在[114.5,124.5)内的频率为
A.0.2 B.0.3 C.0.4 D.0.5
√
解析 在125,120,122,105,130,114,116,95,120,134这10个数中,落在[114.5,124.5)内的有116,120,120,122,共4个,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.在抽查产品尺寸的过程中,将其尺寸分成若干组,[a,b)是其中的一组,该组的频率为m,在频率分布直方图中该组的小长方形的高为h,则|a-b|等于
√
3.容量为100的样本数据,按从小到大的顺序分为8组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
第三组的频数和频率分别是
√
解析 第三组的频数x=100-(10+13+14+15+13+12+9)=100-86=14,频率为 =0.14.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图所示,其中支出(单位:元)在[50,60]内的学生有30人,则n的值为
A.100 B.1 000 C.90 D.900
√
解析 由频率分布直方图可知,
前三组的频率之和为(0.01+0.024+0.036)×10=0.7,
∴支出在[50,60]内的频率为1-0.7=0.3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(多选)根据下面给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)的条形图.以下结论正确的是
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量呈增加趋势
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 从2006年,将每年的二氧化硫排放量与前一年作差比较,得到2008年二氧化硫排放量与2007年排放量的差最大,A选项正确;
从2007年开始二氧化硫排放量变少,B选项正确;
虽然2011年二氧化硫排放量较2010年多一些,但自2006年以来,整体呈递减趋势,C选项正确,D选项错误,故选ABC.
6.在样本的频率分布直方图中,共有5个小长方形,已知中间一个小长方形面积是其余4个小长方形面积之和的 ,且中间一组的频数为10,则样本容量是______.
40
解析 设中间长方形的面积为x,样本容量为n.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
90
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵样本中产品净重小于100克的频率为(0.050+0.100)×2=0.3,频数为36,
∵样本中净重大于或等于98克并且小于104克
的产品的频率为(0.100+0.150+0.125)×2=0.75,
∴样本中净重大于或等于98克并且小于104克的产品的个数为120×0.75=90.
8.某市共有5 000名高三学生参加联考,为了了解这些学生对数学知识的掌握情况,现从中随机抽出苦干名学生在这次测试中的数学成绩,制成频率分布表:
根据右面的频率分布表,可知①处的数值为____,②处的数值为_______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
分组
频数
频率
[80,90)
①
②
[90,100)
?
0.050
[100,110)
?
0.200
[110,120)
36
0.300
[120,130)
?
0.275
[130,140)
12
?
[140,150]
?
0.050
合计
?
?
3
0.025
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②处的数值为1-0.050-0.200-0.300-0.275-0.100-0.050=0.025.
①处的数值为0.025×120=3.
9.一个频数分布表(样本容量为50)不小心被损坏了一部分,只记得样本中数据在[20,60)内的频率为0.6,试计算样本在[40,50),[50,60)内的数据个数之和.
解 根据题意,设分布在[40,50),[50,60)内的数据个数分别为x,y.
∵样本中数据在[20,60)内的频率为0.6,样本容量为50,
解得x+y=21.
即样本在[40,50),[50,60)内的数据个数之和为21.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.从全校参加期末考试的试卷中抽取一个样本,考察成绩(均为整数)的分布,将样本分成5组,绘成频率分布直方图(如图所示),从左到右各小组的小矩形的高之比为2∶3∶6∶4∶1,最左边的一组频数为6.
(1)求样本容量;
解 在频率分布直方图中频数之比等于频率之比且样本的所有频率之和等于1.
小矩形的高之比为频率之比,
∴从左到右各小组的频率之比为2∶3∶6∶4∶1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求105.5~120.5这一组的频数及频率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)如果成绩大于120分为优秀,估计这次考试成绩的优秀率.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,
学生人数为
A.588 B.480 C.450 D.120
√
该模块测试成绩不少于60分的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵少于60分的学生人数为600×(0.05+0.15)=120,
∴不少于60分的学生人数为480.
12.样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是
A.32,0.4 B.8,0.1 C.32,0.1 D.8,0.4
√
解析 样本数据落在[6,10)内的频率为0.08×4=0.32,
则a=100×0.32=32;
由于样本数据落在[2,6)内的频率为0.02×4=0.08,
则样本数据落在[2,10)内的频率b=0.08+0.32=0.4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(多选)某健身房为了解运动健身减肥的效果,调查了20名肥胖者健身前(如直方图(1)所示)后(如直方图(2)所示)的体重(单位:kg)变化情况:
对比数据,关于这20名肥胖者,下面结论正确的是
A.他们健身后,体重在区间[90,100)内的
人数较健身前增加了2人
B.他们健身后,体重原在区间[100,110)
内的人员一定无变化
C.他们健身后,20人的平均体重大约减少
了8 kg
D.他们健身后,原来体重在区间[110,120]内的肥胖者体重都有减少
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 体重在区间[90,100)内的肥胖者由健身前的6人增加到健身后的8人,增加了2人,故A正确;
他们健身后,体重在区间[100,110]内的频率没有变,但人员组成可能改变,故B错误;
他们健身后,20人的平均体重大约减少了(0.3×95+0.5×105+0.2×115)-(0.1×85+0.4×95+0.5×105)=5 kg,故C错误;
因为图(2)中没有体重在区间[110,120]内的人员,所以原来体重在区间[110,120]内的肥胖者体重都有减少,故D正确.故选AD.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.为了解某地居民的月收入情况,一个社会调查机构调查了20 000人,并根据所得数据画出样本的频率分布直方图如图所示(最后一组包含两端值,其他组包含最小值,不包含最大值).现按月收入分层,用分层随机抽样的方法在这20 000人中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
抽出200人进一步调查,则月收入在[1 500,2 000)(单位:元)内的应抽取_____人.
40
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 月收入在[1 500,2 000)内的频率为1-(0.000 2+0.000 5×2+0.000 3+0.000 1)×500=0.2,故应抽取200×0.2=40(人).
拓广探究
15.某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则
(1)图中的x=________;
解析 由频率分布直方图知20x=1-20×(0.025+0.006 5+0.003+0.003),解得x=0.012 5.
0.012 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若上学所需时间不少于1小时的学生可申请在学校住宿,则该校600名新生中估计有_____名学生可以申请住宿.
72
解析 上学时间不少于1小时的学生的频率为0.003×2×20=0.12,
因此估计有0.12×600=72(人)可以申请住宿.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.某电视台随机在本省内15~65岁的人群中抽取了n人回答问题“本省内著名旅游景点有哪些”,统计结果如图表所示.
组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y
(1)分别求出a,b,x,y的值;
组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y
解 由频率表中第4组数据可知,第4组总人数为 =25,
再结合频率分布直方图可知n=
=100,
所以a=100×0.01×10×0.5=5,
b=100×0.03×10×0.9=27,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)从第2,3,4组回答正确的人中用分层随机抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y
解 第2,3,4组回答正确的共有18+27+9=54(人).
利用分层随机抽样在54人中抽取6人,
组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
9.2.1 总体取值规律的估计
学习目标
XUE XI MU BIAO
1.掌握频率分布表的作法以及频率分布直方图的画法.
2.掌握用频率分布直方图估计总体.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 频率分布直方图
作频率分布直方图的步骤
(1)求极差:极差为一组数据中最大值与最小值的 .
(2)决定组距与组数
将数据分组时,一般取 组距,并且组距应力求“取整”,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.
(3)将数据分组
差
等长
高度
思考 要做频率分布表,需要对原始数据做哪些工作?
答案 分组,频数累计,计算频数和频率.
知识点二 其它统计图表
统计图表
主要应用
扇形图
直观描述各类数据占 的比例
条形图和直方图
直观描述不同类别或分组数据的___________
折线图
描述 随时间的变化趋势
总数
频数和频率
数据
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.频率分布直方图中小长方形的高表示该组上的个体在样本中出现的频率与组距的比值.( )
2.频率分布直方图中小长方形的面积表示该组的个体数.( )
3.频率分布直方图中所有小长方形面积之和为1.( )
4.样本容量越大,用样本的频率分布去估计总体的频率分布就越准确.
( )
√
×
√
√
2
题型探究
PART TWO
例1 从某校高三学生中抽取50名参加数学竞赛,成绩分组(单位:分)及各组的频数如下:
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表(含累积频率);
一、画频率分布直方图
解 频率分布表如下:
成绩分组
频数
频率
累积频率
[40,50)
2
0.04
0.04
[50,60)
3
0.06
0.1
[60,70)
10
0.2
0.3
[70,80)
15
0.3
0.6
[80,90)
12
0.24
0.84
[90,100]
8
0.16
1.00
合计
50
1.00
?
(2)画出频率分布直方图;
解 频率分布直方图如图所示.
(3)估计成绩在[60,90)分的学生比例.
解 学生成绩在[60,90)分的频率为0.2+0.3+0.24=0.74=74%,
所以估计成绩在[60,90)分的学生比例为74%.
反思感悟
绘制频率分布直方图的注意点
(1)各组频率的和等于1,因此,各小矩形的面积之和也等于1.
(3)同样一组数据,如果组距不同,横轴、纵轴单位不同,得到的频率分布直方图的形状也会不同.
跟踪训练1 为了了解九年级学生中女生的身高(单位:cm)情况,某中学对九年级部分女生身高进行了一次测量,所得数据整理后列出的频率分布表如右:
(1)求出表中m,n,M,N所表示的数分别是多少;
分组
频数
频率
[145.5,149.5)
1
0.02
[149.5,153.5)
4
0.08
[153.5,157.5)
20
0.40
[157.5,161.5)
15
0.30
[161.5,165.5)
8
0.16
[165.5,169.5]
m
n
合计
M
N
∴m=2,M=1+4+20+15+8+2=50.
(2)画出频率分布直方图;
解 作出直角坐标系,组距为4,纵轴表示 ,横轴表示身高,画出频率分布直方图如图所示.
(3)全体女生中身高在哪组范围内的人数最多?估计九年级学生中女生的身高在161.5 cm以上的频率.
解 由频率分布直方图可知,样本中身高在[153.5,157.5)范围内的人数最多,且身高在161.5 cm以上的频率为0.16+0.04=0.20,由此可估计全体女生中身高在[153.5,157.5)范围内的人数最多,九年级学生中女生的身高在161.5 cm以上的频率为0.20.
二、频率分布直方图的应用
例2 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?
样本容量是多少?
解 频率分布直方图是以面积的形式来反映数据落在各小组内的频率大小的,
(2)若次数在110以上(含110次)为达标,则该校高一年级全体学生的达标率约是多少?
反思感悟
(1)频率分布直方图的性质
①因为小矩形的面积=组距× =频率,所以各小矩形的
面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小组内的频率大小.
②在频率分布直方图中,各小矩形的面积之和等于1.
③ =样本容量.
(2)频率分布直方图反映了样本在各个范围内取值的可能性,由抽样的代表性利用样本在某一范围内的频率,可近似地估计总体在这一范围内的可能性.
跟踪训练2 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100?
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的比例;
解 根据频数分布表知,100名学生中一周课外阅读时间不少于12小时的学生共有6+2+2=10(名),
所以样本中的学生一周课外阅读时间少于12小时的频率是1- =0.9.
故从该校随机选取一名学生,估计其该周课外阅读时间少于12小时的比例为0.9.
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100?
(2)求频率分布直方图中a,b的值;
课外阅读时间落在[8,10)组内的有25人,频率为0.25,
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论).
解 样本中的100名学生该周课外阅读时间的平均数在第4组.
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18]
2
合计
100?
三、折线图、条形图、扇形图及应用
例3 如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计图和条形统计图.
解 该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期
1
2
3
4
5
6
7
8
9
10
最低气温(℃)
-3
-2
0
-1
1
2
0
-1
2
2
其中最低气温为-3 ℃的有1天,占10%,最低气温为-2 ℃的有1天,占10%,最低气温为-1 ℃的有2天,占20%,最低气温为0 ℃的有2天,占20%,最低气温为1 ℃的有1天,占10%,最低气温为2 ℃的有3天,占30%,扇形统计图如图所示.
条形统计图如图所示:
反思感悟
(1)条形图是用一个单位长度表示一定的数量或频率,根据数量的多少或频率的大小画成长短不同的矩形条,条形图能清楚地表示出每个项目的具体数目或频率.
(2)扇形图是用整个圆面积表示总数(100%),用圆内的扇形面积表示各个部分所占总数的百分数.
(3)在画折线图时,要注意明确横轴、纵轴的实际含义.
跟踪训练3 华为、抖音海外版事件暴露了我国计算机行业中芯片、软件两大短板,为防止“卡脖子”事件的再次发生,科技专业人才就成了决胜的关键.为了解我国在芯片、软件方面的潜力,某调查机构对我国若干大型科技公司进行调查统计,得到了这两个行业从业者的年龄分布的饼形图和“90后”从事这两个行业的岗位分布雷达图,
则下列说法中不一定正确的是
A.芯片、软件行业从业者中,“90后”占总人数的比例超过50%
B.芯片、软件行业中从事技术、设计岗位的“90后”人数超过总人数
的25%
C.芯片、软件行业从事技术岗位的人中,“90后”比“80后”多
D.芯片、软件行业中,“90后”从事市场岗位的人数比“80前”的总
人数多
√
解析 对于选项A,芯片、软件行业从业者中“90后”占总人数的55%,故选项A正确;
对于选项B,芯片、软件行业中从事技术、设计岗位的“90后”占总人数的(37%+13%)×55%=27.5%,故选项B正确;
对于选项C,芯片、软件行业中从事技术岗位的“90后”占总人数的37%×55%=20.35%,“80后”占总人数的40%,但从事技术的“80后”占总人数的百分比不知道,无法确定二者人数多少,故选项C错误;
对于选项D,芯片、软件行业中从事市场岗位的“90后”占总人数的14%×55%=7.7%,“80前”占总人数的5%,故选项D正确.
3
随堂演练
PART THREE
1
2
3
4
5
1.用样本频率分布估计总体频率分布的过程中,下列说法正确的是
A.总体容量越大,估计越精确
B.总体容量越小,估计越精确
C.样本容量越大,估计越精确
D.样本容量越小,估计越精确
√
解析 用样本的频率分布估计总体的频率分布时,在总体一定时,样本的容量越大,估计就越精确.
2.一个容量为20的样本数据,分组与频数如下表:
分组
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
[60,70]
频数
2
3
4
5
4
2
则样本在[10,50)内的频率为
A.0.5 B.0.24 C.0.6 D.0.7
√
解析 因为样本在[10,50)内的频数为2+3+4+5=14,样本容量为20,
1
2
3
4
5
3.(多选)容量为100的样本,其数据分布在[2,18]内,将样本数据分为4组:[2,6),[6,10),[10,14),[14,18],得到频率分布直方图如图所示,则下列说法中正确的是
A.样本数据分布在[6,10)内的频率为0.32
B.样本数据分布在[10,14)内的频数为40
C.样本数据分布在[2,10)内的频数为40
D.估计总体数据大约有10%分布在[10,14)内
√
√
√
1
2
3
4
5
1
2
3
4
5
对于C,由题图可得,样本数据分布在[2,10)内的频数为100×(0.02+0.08)×4=40,所以C正确.
对于D,由题图可估计,总体数据分布在[10,14)内的比例为0.1×4=0.4=40%,所以D错误,故选ABC.
解析 对于A,由题图可得,样本数据分布在[6,10)内的频率为0.08×4=0.32,所以A正确.
对于B,由题图可得,样本数据分布在[10,14)内的频数为100×(0.1×4)=40,所以B正确.
4.某地政府调查了工薪阶层1 000人的月工资,并根据调查结果画出如图所示的频率分布直方图,为了了解工薪阶层对月工资的满意程度,要用分层随机抽样的方法从调查的1 000人中抽出100人做电话询访,则月工资在区间[30,35)内的工薪阶层应抽出_____人.
15
解析 月工资落在区间[30,35)内的频率为1-(0.02+0.04+0.05+0.05+0.01)×5=0.15,
所以月工资在区间[30,35)内的工薪阶层应抽出100×0.15=15(人).
1
2
3
4
5
5.为了解今年某校高三毕业班准备报考飞行员学生的体重(单位:千克)情况,将所得的数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前三个小组的频率之比为1∶2∶3,其中第2小组的频数为12.则该校报考飞行员的总人数为_____.
48
1
2
3
4
5
解析 设报考飞行员的总人数为n,
设第1小组的频率为a,
则有a+2a+3a+(0.013+0.037)×5=1,
解得a=0.125,
所以第2小组的频率为0.25.
又第2小组的频数为12,
1
2
3
4
5
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)频数与频率.
(2)频率分布表.
(3)频率分布直方图.
(4)扇形图、条形图和折线图.
2.方法归纳:图表识别、数据分析.
3.常见误区:频率分布直方图中小矩形的高以及小矩形的面积代表的意义理解不清.
4
课时对点练
PART FOUR
基础巩固
1.从一堆苹果中任取10个,称得它们的质量如下(单位:克):125 120 122 105 130 114 116 95 120 134
则样本数据落在[114.5,124.5)内的频率为
A.0.2 B.0.3 C.0.4 D.0.5
√
解析 在125,120,122,105,130,114,116,95,120,134这10个数中,落在[114.5,124.5)内的有116,120,120,122,共4个,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.在抽查产品尺寸的过程中,将其尺寸分成若干组,[a,b)是其中的一组,该组的频率为m,在频率分布直方图中该组的小长方形的高为h,则|a-b|等于
√
3.容量为100的样本数据,按从小到大的顺序分为8组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
第三组的频数和频率分别是
√
解析 第三组的频数x=100-(10+13+14+15+13+12+9)=100-86=14,频率为 =0.14.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图所示,其中支出(单位:元)在[50,60]内的学生有30人,则n的值为
A.100 B.1 000 C.90 D.900
√
解析 由频率分布直方图可知,
前三组的频率之和为(0.01+0.024+0.036)×10=0.7,
∴支出在[50,60]内的频率为1-0.7=0.3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(多选)根据下面给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)的条形图.以下结论正确的是
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量呈增加趋势
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 从2006年,将每年的二氧化硫排放量与前一年作差比较,得到2008年二氧化硫排放量与2007年排放量的差最大,A选项正确;
从2007年开始二氧化硫排放量变少,B选项正确;
虽然2011年二氧化硫排放量较2010年多一些,但自2006年以来,整体呈递减趋势,C选项正确,D选项错误,故选ABC.
6.在样本的频率分布直方图中,共有5个小长方形,已知中间一个小长方形面积是其余4个小长方形面积之和的 ,且中间一组的频数为10,则样本容量是______.
40
解析 设中间长方形的面积为x,样本容量为n.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
90
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵样本中产品净重小于100克的频率为(0.050+0.100)×2=0.3,频数为36,
∵样本中净重大于或等于98克并且小于104克
的产品的频率为(0.100+0.150+0.125)×2=0.75,
∴样本中净重大于或等于98克并且小于104克的产品的个数为120×0.75=90.
8.某市共有5 000名高三学生参加联考,为了了解这些学生对数学知识的掌握情况,现从中随机抽出苦干名学生在这次测试中的数学成绩,制成频率分布表:
根据右面的频率分布表,可知①处的数值为____,②处的数值为_______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
分组
频数
频率
[80,90)
①
②
[90,100)
?
0.050
[100,110)
?
0.200
[110,120)
36
0.300
[120,130)
?
0.275
[130,140)
12
?
[140,150]
?
0.050
合计
?
?
3
0.025
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②处的数值为1-0.050-0.200-0.300-0.275-0.100-0.050=0.025.
①处的数值为0.025×120=3.
9.一个频数分布表(样本容量为50)不小心被损坏了一部分,只记得样本中数据在[20,60)内的频率为0.6,试计算样本在[40,50),[50,60)内的数据个数之和.
解 根据题意,设分布在[40,50),[50,60)内的数据个数分别为x,y.
∵样本中数据在[20,60)内的频率为0.6,样本容量为50,
解得x+y=21.
即样本在[40,50),[50,60)内的数据个数之和为21.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.从全校参加期末考试的试卷中抽取一个样本,考察成绩(均为整数)的分布,将样本分成5组,绘成频率分布直方图(如图所示),从左到右各小组的小矩形的高之比为2∶3∶6∶4∶1,最左边的一组频数为6.
(1)求样本容量;
解 在频率分布直方图中频数之比等于频率之比且样本的所有频率之和等于1.
小矩形的高之比为频率之比,
∴从左到右各小组的频率之比为2∶3∶6∶4∶1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求105.5~120.5这一组的频数及频率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)如果成绩大于120分为优秀,估计这次考试成绩的优秀率.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,
学生人数为
A.588 B.480 C.450 D.120
√
该模块测试成绩不少于60分的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵少于60分的学生人数为600×(0.05+0.15)=120,
∴不少于60分的学生人数为480.
12.样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是
A.32,0.4 B.8,0.1 C.32,0.1 D.8,0.4
√
解析 样本数据落在[6,10)内的频率为0.08×4=0.32,
则a=100×0.32=32;
由于样本数据落在[2,6)内的频率为0.02×4=0.08,
则样本数据落在[2,10)内的频率b=0.08+0.32=0.4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(多选)某健身房为了解运动健身减肥的效果,调查了20名肥胖者健身前(如直方图(1)所示)后(如直方图(2)所示)的体重(单位:kg)变化情况:
对比数据,关于这20名肥胖者,下面结论正确的是
A.他们健身后,体重在区间[90,100)内的
人数较健身前增加了2人
B.他们健身后,体重原在区间[100,110)
内的人员一定无变化
C.他们健身后,20人的平均体重大约减少
了8 kg
D.他们健身后,原来体重在区间[110,120]内的肥胖者体重都有减少
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 体重在区间[90,100)内的肥胖者由健身前的6人增加到健身后的8人,增加了2人,故A正确;
他们健身后,体重在区间[100,110]内的频率没有变,但人员组成可能改变,故B错误;
他们健身后,20人的平均体重大约减少了(0.3×95+0.5×105+0.2×115)-(0.1×85+0.4×95+0.5×105)=5 kg,故C错误;
因为图(2)中没有体重在区间[110,120]内的人员,所以原来体重在区间[110,120]内的肥胖者体重都有减少,故D正确.故选AD.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.为了解某地居民的月收入情况,一个社会调查机构调查了20 000人,并根据所得数据画出样本的频率分布直方图如图所示(最后一组包含两端值,其他组包含最小值,不包含最大值).现按月收入分层,用分层随机抽样的方法在这20 000人中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
抽出200人进一步调查,则月收入在[1 500,2 000)(单位:元)内的应抽取_____人.
40
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 月收入在[1 500,2 000)内的频率为1-(0.000 2+0.000 5×2+0.000 3+0.000 1)×500=0.2,故应抽取200×0.2=40(人).
拓广探究
15.某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则
(1)图中的x=________;
解析 由频率分布直方图知20x=1-20×(0.025+0.006 5+0.003+0.003),解得x=0.012 5.
0.012 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若上学所需时间不少于1小时的学生可申请在学校住宿,则该校600名新生中估计有_____名学生可以申请住宿.
72
解析 上学时间不少于1小时的学生的频率为0.003×2×20=0.12,
因此估计有0.12×600=72(人)可以申请住宿.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.某电视台随机在本省内15~65岁的人群中抽取了n人回答问题“本省内著名旅游景点有哪些”,统计结果如图表所示.
组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y
(1)分别求出a,b,x,y的值;
组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y
解 由频率表中第4组数据可知,第4组总人数为 =25,
再结合频率分布直方图可知n=
=100,
所以a=100×0.01×10×0.5=5,
b=100×0.03×10×0.9=27,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)从第2,3,4组回答正确的人中用分层随机抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y
解 第2,3,4组回答正确的共有18+27+9=54(人).
利用分层随机抽样在54人中抽取6人,
组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
