5.3.1平行线的性质 同步练习(含答案)
文档属性
| 名称 | 5.3.1平行线的性质 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 934.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
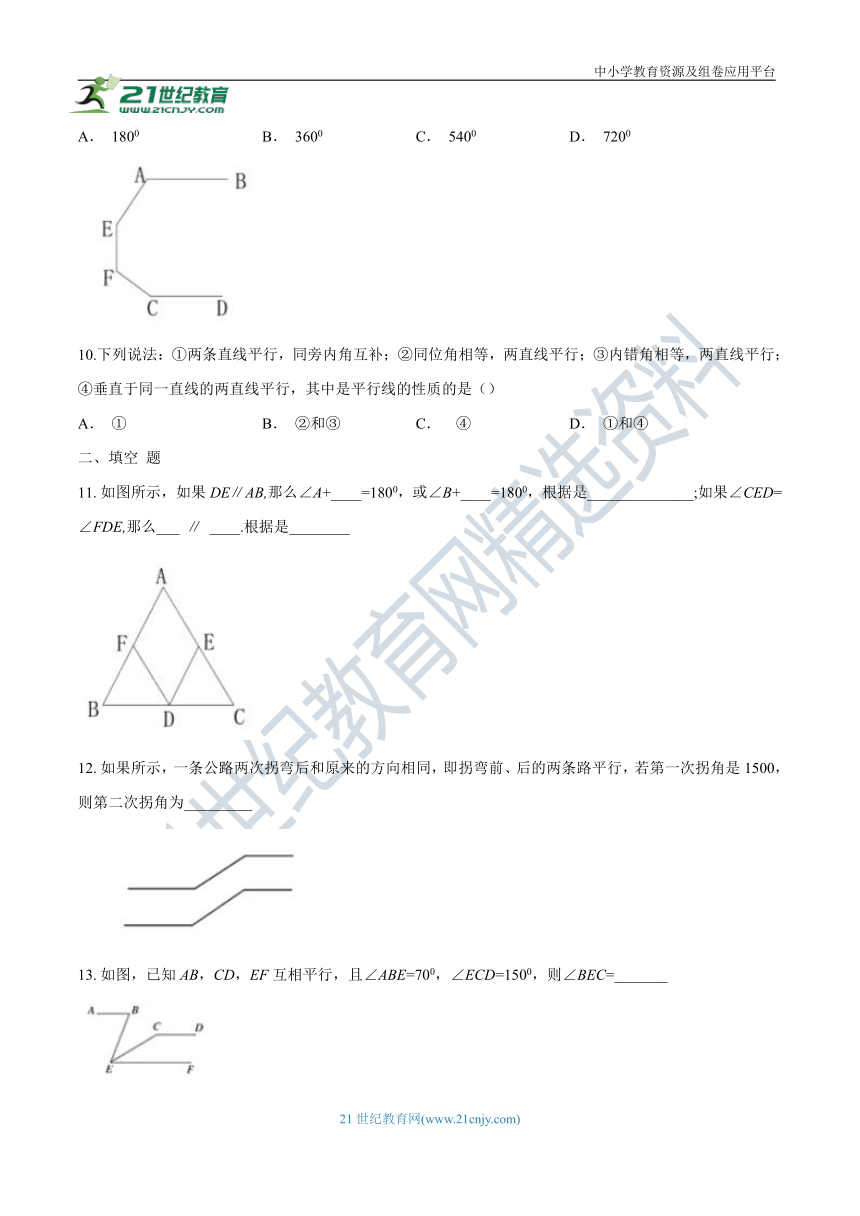
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 21:34:01 | ||
图片预览


文档简介
5.3.1平行线的性质同步练习
一、选择题
1. 如图所示,AB∥CD,则与∠1相等的角(∠1除外)共有()
A.5个 B. 4个 C. 3个 D. 2个
2.如图所示,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=600,则∠BOF为()
A. 350 B. 300 C. 250 D. 200
3.如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需再有下列条件中的()即可。
A. ∠1=∠2 B. ∠1=∠DFE C. ∠1=∠AFD D. ∠2=∠AFD
4.如图,过△ABC的边BC上一点D作DF∥AC,若∠A=400,∠B=600,则∠FDB的度数为()
A. 400 B. 600 C. 100 D. 1200
5.如图,直线a∥b,则∠A的度数是()
A.280 B. 310 C. 390 D. 420
6.如图,将三角板的直角顶点放在直尺的一边上,∠1=300,∠2=500,∠3=()
A. 100 B. 200 C. 300 D. 500
7.一条船停在海面上,从船上看灯塔位于北偏东600方向,那么从灯塔看船位于灯塔的____方向()
A. 南偏西600 B.西偏南600 C. 南偏西300 D. 北偏西300
如图,已知a∥b,把三角尺的直角顶点放在直线a上。若∠1=400,则∠2的度数为()
A.1300 B. 1400 C. 1450 D. 1500
8.如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角(∠1除外)共有()
A. 6个 B. 5个 C. 4个 D. 3个
9.如图,AB∥CD,则∠A+∠E+∠F等于()
A. 1800 B. 3600 C. 5400 D. 7200
10.下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是()
A. ① B. ②和③ C. ④ D. ①和④
二、填空 题
11. 如图所示,如果DE∥AB,那么∠A+____=1800,或∠B+____=1800,根据是______________;如果∠CED=∠FDE,那么___ ∥ ____.根据是________
12. 如果所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、后的两条路平行,若第一次拐角是1500,则第二次拐角为_________
13. 如图,已知AB,CD,EF互相平行,且∠ABE=700,∠ECD=1500,则∠BEC=_______
14. 如图,直线l1∥l2且l1,l2被直线l3所截,∠1=∠2=350,∠P=900,则∠3=_____度
15. 将一副学生用三角板按如图所示的位置放置,若AE∥BC,则∠DAF的度数是_____。
16. 如图所示,AB∥CD,∠1=1150,∠3=1400,则∠2=________.
三、解答题
17.如图,已知∠ABC=1800–∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=360,求∠EFC的度数。
18.如图,EF∥BC,AC平分∠BAF,∠B=800.求∠C的度数.
19.如图,已知a∥b,c、d是截线,若∠1=800,∠5=700.求∠2、∠3、∠4各是多少度?为什么?
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
C
B
B
C
C
B
A
B
C
A
二、填空题
11.∠AED, ∠BDE,两直线平行,同旁内角互补;DF AB,内错角相等,两直线平行
12.1500
13.400
14.550
15.150
16.750
三、解答题
17.解析:(1)∵∠ABC=1800–∠A(已知)
∴∠ABC+∠A=1800
∴AD∥BC(同旁内角互补,两直线平行)
(3)由(1)得AD∥BC
∴∠DBC=∠ADB=360(两直线平行,内错角相等)
∵BD⊥CD,EF⊥CD(已知)
∴∠BDC=∠FEC=900(垂直定义)
∴BD∥FE(同位角相等,两直线平行)
∴∠EFC=∠DBC=360
18.解析:∵EF∥BC(已知)
∴∠B+∠BAF=1800(两直线平行,同旁内角互补)
∵∠B=800
∴∠BAF=1800–800=1000
∵AC平分∠BAF,(已知)
∴∠CAF=false∠BAF=500(角平线定义)
∴∠C=∠CAF=500(两直线平行,内错角相等)
19.解析:∵a∥b(已知)
∴∠2=∠1=800(两直线平行,内错角相等)
∠5+∠3=1800(两直线平行,同旁内角互补)
∵∠5=700
∴∠3=1100
∵∠4+∠5=1800
∴∠4=1100
一、选择题
1. 如图所示,AB∥CD,则与∠1相等的角(∠1除外)共有()
A.5个 B. 4个 C. 3个 D. 2个
2.如图所示,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=600,则∠BOF为()
A. 350 B. 300 C. 250 D. 200
3.如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需再有下列条件中的()即可。
A. ∠1=∠2 B. ∠1=∠DFE C. ∠1=∠AFD D. ∠2=∠AFD
4.如图,过△ABC的边BC上一点D作DF∥AC,若∠A=400,∠B=600,则∠FDB的度数为()
A. 400 B. 600 C. 100 D. 1200
5.如图,直线a∥b,则∠A的度数是()
A.280 B. 310 C. 390 D. 420
6.如图,将三角板的直角顶点放在直尺的一边上,∠1=300,∠2=500,∠3=()
A. 100 B. 200 C. 300 D. 500
7.一条船停在海面上,从船上看灯塔位于北偏东600方向,那么从灯塔看船位于灯塔的____方向()
A. 南偏西600 B.西偏南600 C. 南偏西300 D. 北偏西300
如图,已知a∥b,把三角尺的直角顶点放在直线a上。若∠1=400,则∠2的度数为()
A.1300 B. 1400 C. 1450 D. 1500
8.如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角(∠1除外)共有()
A. 6个 B. 5个 C. 4个 D. 3个
9.如图,AB∥CD,则∠A+∠E+∠F等于()
A. 1800 B. 3600 C. 5400 D. 7200
10.下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是()
A. ① B. ②和③ C. ④ D. ①和④
二、填空 题
11. 如图所示,如果DE∥AB,那么∠A+____=1800,或∠B+____=1800,根据是______________;如果∠CED=∠FDE,那么___ ∥ ____.根据是________
12. 如果所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、后的两条路平行,若第一次拐角是1500,则第二次拐角为_________
13. 如图,已知AB,CD,EF互相平行,且∠ABE=700,∠ECD=1500,则∠BEC=_______
14. 如图,直线l1∥l2且l1,l2被直线l3所截,∠1=∠2=350,∠P=900,则∠3=_____度
15. 将一副学生用三角板按如图所示的位置放置,若AE∥BC,则∠DAF的度数是_____。
16. 如图所示,AB∥CD,∠1=1150,∠3=1400,则∠2=________.
三、解答题
17.如图,已知∠ABC=1800–∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=360,求∠EFC的度数。
18.如图,EF∥BC,AC平分∠BAF,∠B=800.求∠C的度数.
19.如图,已知a∥b,c、d是截线,若∠1=800,∠5=700.求∠2、∠3、∠4各是多少度?为什么?
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
C
B
B
C
C
B
A
B
C
A
二、填空题
11.∠AED, ∠BDE,两直线平行,同旁内角互补;DF AB,内错角相等,两直线平行
12.1500
13.400
14.550
15.150
16.750
三、解答题
17.解析:(1)∵∠ABC=1800–∠A(已知)
∴∠ABC+∠A=1800
∴AD∥BC(同旁内角互补,两直线平行)
(3)由(1)得AD∥BC
∴∠DBC=∠ADB=360(两直线平行,内错角相等)
∵BD⊥CD,EF⊥CD(已知)
∴∠BDC=∠FEC=900(垂直定义)
∴BD∥FE(同位角相等,两直线平行)
∴∠EFC=∠DBC=360
18.解析:∵EF∥BC(已知)
∴∠B+∠BAF=1800(两直线平行,同旁内角互补)
∵∠B=800
∴∠BAF=1800–800=1000
∵AC平分∠BAF,(已知)
∴∠CAF=false∠BAF=500(角平线定义)
∴∠C=∠CAF=500(两直线平行,内错角相等)
19.解析:∵a∥b(已知)
∴∠2=∠1=800(两直线平行,内错角相等)
∠5+∠3=1800(两直线平行,同旁内角互补)
∵∠5=700
∴∠3=1100
∵∠4+∠5=1800
∴∠4=1100
