5.2.2平行线的判定 同步练习(含答案)
文档属性
| 名称 | 5.2.2平行线的判定 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 941.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 21:06:53 | ||
图片预览

文档简介
11620500111760005.2.2平行线的判定同步练习
一、选择题
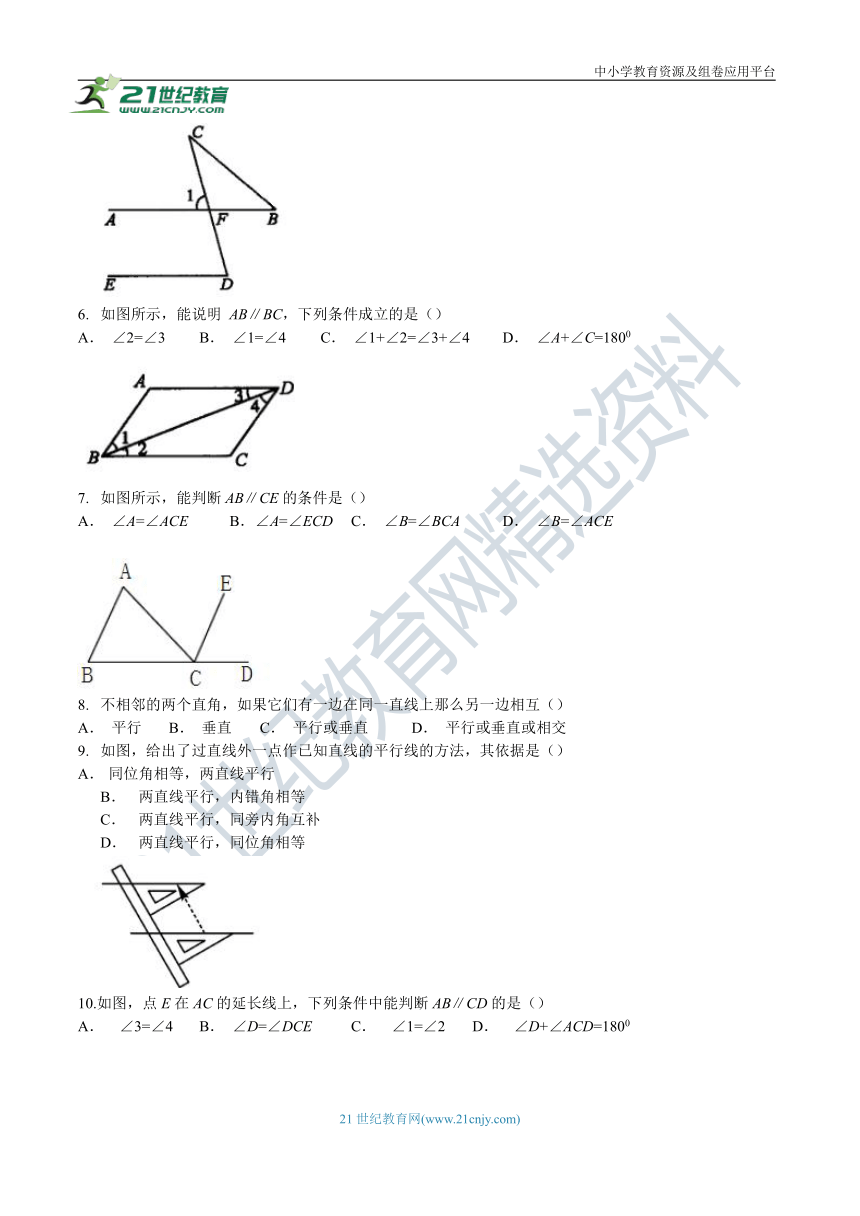
1. 如图,下列条件中能判定直线l1∥l2的是()
A. ∠1=∠2 B. ∠1=∠5 C.∠1+∠3=1800 D.∠3=∠5
2. 如图,下列条件中,能判定DE∥AC的是()
A. ∠EDC=∠EFC B. ∠AFE=∠ACD C. ∠1=∠2 D. ∠3=∠4
3. 如图,∠1=∠2,则下列结论正确的是()
A. AD∥BC B. AB∥CD C. EF∥AD D. EF∥BC
4. 如图所示,下列条件中,能判定AB∥CD的是()
A. ∠BAD=∠BCD B. ∠1=∠2 C. ∠3=∠4 D. ∠BAC=∠ACD
5. 如图所示,能说明AB∥DE的有()
①∠1=∠D; ②∠CFB+∠D=1800;③∠B=∠D;④∠BFD=∠ D.
A.1个 B.2个 C. 3个 D. 4个
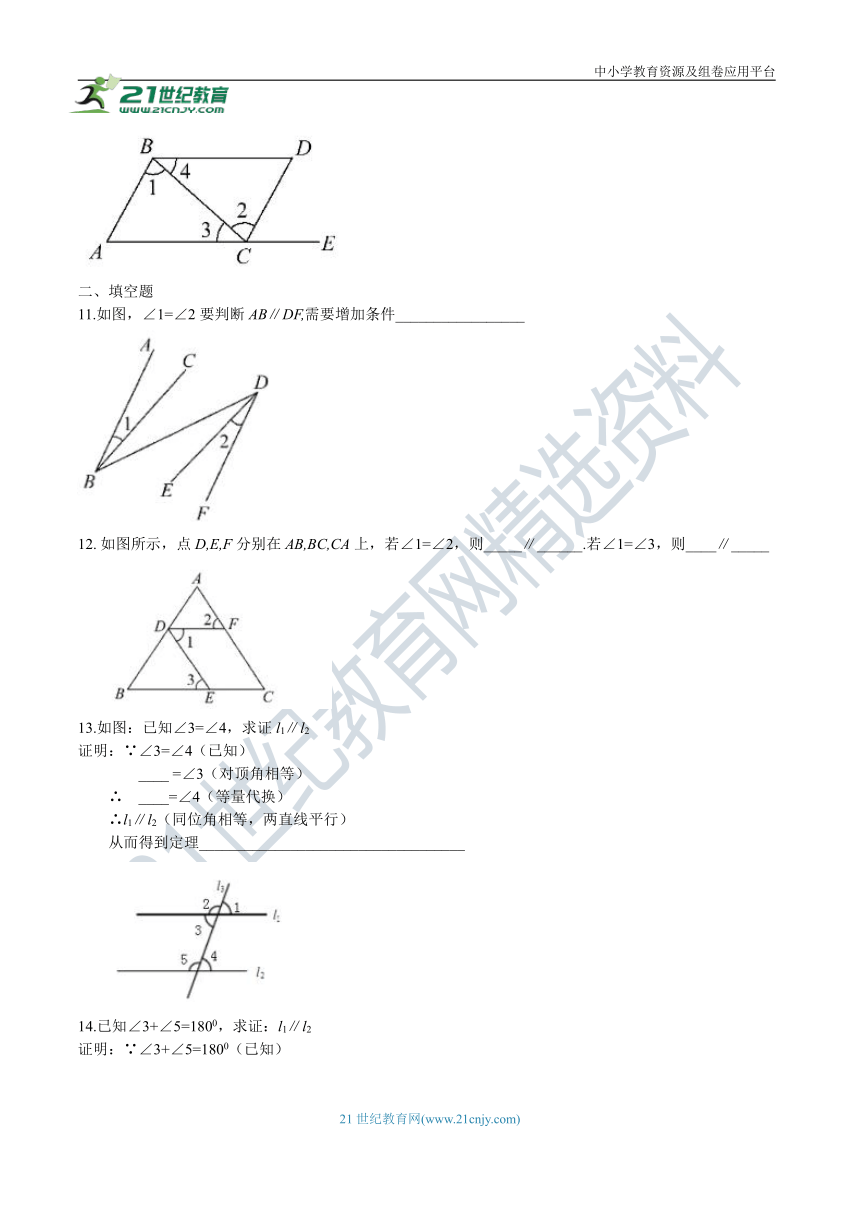
6. 如图所示,能说明 AB∥BC,下列条件成立的是()
A. ∠2=∠3 B. ∠1=∠4 C. ∠1+∠2=∠3+∠4 D. ∠A+∠C=1800
7. 如图所示,能判断AB∥CE的条件是()
A. ∠A=∠ACE B.∠A=∠ECD C. ∠B=∠BCA D. ∠B=∠ACE
8. 不相邻的两个直角,如果它们有一边在同一直线上那么另一边相互()
A. 平行 B. 垂直 C. 平行或垂直 D. 平行或垂直或相交
9. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是()
A. 同位角相等,两直线平行
B. 两直线平行,内错角相等
C. 两直线平行,同旁内角互补
D. 两直线平行,同位角相等
10.如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是()
A. ∠3=∠4 B. ∠D=∠DCE C. ∠1=∠2 D. ∠D+∠ACD=1800
二、填空题
11.如图,∠1=∠2要判断AB∥DF,需要增加条件_________________
12. 如图所示,点D,E,F分别在AB,BC,CA上,若∠1=∠2,则_____∥______.若∠1=∠3,则____∥_____
13.如图:已知∠3=∠4,求证l1∥l2
证明:∵∠3=∠4(已知)
____ =∠3(对顶角相等)
∴ ____=∠4(等量代换)
∴l1∥l2(同位角相等,两直线平行)
从而得到定理___________________________________
14.已知∠3+∠5=1800,求证:l1∥l2
证明:∵∠3+∠5=1800(已知)
____+∠5=1800(邻补角定义)
∴∠3=____(同角的补角相等)
∴l1∥l2(内错相等,两直线平行)
从而得到定理_______________________________
15.如图:
(1)如果∠1=∠B,那么___ ∥ ____
根据是_________________
(2)如果∠4+∠D=1800,那么___ ∥ ____
根据是_________________
(3)如果∠3=∠D,那么___ ∥ ____
根据是_________________
(4)如果∠B+___=1800,那么AB ∥ CD
根据是_________________
(5)要使BE∥DF,必须∠1=___,
根据是_________________
三、解答题
16.如图,∠B=∠C,∠B+∠D=1800,那么BC平行于DE吗?为什么?
17.如图,AF,CE,BD交于点B,且BE平分∠DBF,且∠1=∠C,问BD与AC平行吗?为什么?
18.如图,AD平分∠BAC, EF平分∠DEC,且∠1=∠2,试说明DE与AB的位置关系。
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
C
D
C
D
C
A
A
A
A
C
二、填空题
11. ∠ABD=∠BDF(或∠CBD=∠BDE)
12.AC DE , DF BC
13.∠1 , ∠1 内错角相等,两直线平行
14.∠4 , ∠4 同旁内角互补,两直线平行
15.(1)AB CD 同位角相等,两直线平行(2)BE DF 同旁内角互补,两直线平行
(3)BE DF 内错角相等,两直线平行(4)∠2,同旁内角互补,两直线平行(5)∠D,同位角相等,两直线平行
16.解析:BC∥DE,理由如下:
∵∠B=∠C,∠B+∠D=1800,
∴∠C+∠D=1800,(等量代换)
∴BC∥DE(同旁内角互补,两直线平行)
17.解析:BD∥AC,理由 如下:
∵BE平分∠DBF,
∴∠1=∠EBD(角平分线定义)
∵∠1=∠C
∴∠C=∠EBD(等量代换)
∴BD∥AC(同位角相等,两直线平行)
18.
解析:DE∥AB,理由 如下:
∵AD平分∠BAC,(已知)
∴∠BAC=2∠1.(角平线的定义 )
∵EF平分∠DEC,(已知)
∴∠DEC=2∠2.(角平线的定义 )
∵∠1=∠2(已知)
∴∠BAC=∠DEC(等量代换)
∴DE∥AB(同位角相等,两直线平行)
一、选择题
1. 如图,下列条件中能判定直线l1∥l2的是()
A. ∠1=∠2 B. ∠1=∠5 C.∠1+∠3=1800 D.∠3=∠5
2. 如图,下列条件中,能判定DE∥AC的是()
A. ∠EDC=∠EFC B. ∠AFE=∠ACD C. ∠1=∠2 D. ∠3=∠4
3. 如图,∠1=∠2,则下列结论正确的是()
A. AD∥BC B. AB∥CD C. EF∥AD D. EF∥BC
4. 如图所示,下列条件中,能判定AB∥CD的是()
A. ∠BAD=∠BCD B. ∠1=∠2 C. ∠3=∠4 D. ∠BAC=∠ACD
5. 如图所示,能说明AB∥DE的有()
①∠1=∠D; ②∠CFB+∠D=1800;③∠B=∠D;④∠BFD=∠ D.
A.1个 B.2个 C. 3个 D. 4个
6. 如图所示,能说明 AB∥BC,下列条件成立的是()
A. ∠2=∠3 B. ∠1=∠4 C. ∠1+∠2=∠3+∠4 D. ∠A+∠C=1800
7. 如图所示,能判断AB∥CE的条件是()
A. ∠A=∠ACE B.∠A=∠ECD C. ∠B=∠BCA D. ∠B=∠ACE
8. 不相邻的两个直角,如果它们有一边在同一直线上那么另一边相互()
A. 平行 B. 垂直 C. 平行或垂直 D. 平行或垂直或相交
9. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是()
A. 同位角相等,两直线平行
B. 两直线平行,内错角相等
C. 两直线平行,同旁内角互补
D. 两直线平行,同位角相等
10.如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是()
A. ∠3=∠4 B. ∠D=∠DCE C. ∠1=∠2 D. ∠D+∠ACD=1800
二、填空题
11.如图,∠1=∠2要判断AB∥DF,需要增加条件_________________
12. 如图所示,点D,E,F分别在AB,BC,CA上,若∠1=∠2,则_____∥______.若∠1=∠3,则____∥_____
13.如图:已知∠3=∠4,求证l1∥l2
证明:∵∠3=∠4(已知)
____ =∠3(对顶角相等)
∴ ____=∠4(等量代换)
∴l1∥l2(同位角相等,两直线平行)
从而得到定理___________________________________
14.已知∠3+∠5=1800,求证:l1∥l2
证明:∵∠3+∠5=1800(已知)
____+∠5=1800(邻补角定义)
∴∠3=____(同角的补角相等)
∴l1∥l2(内错相等,两直线平行)
从而得到定理_______________________________
15.如图:
(1)如果∠1=∠B,那么___ ∥ ____
根据是_________________
(2)如果∠4+∠D=1800,那么___ ∥ ____
根据是_________________
(3)如果∠3=∠D,那么___ ∥ ____
根据是_________________
(4)如果∠B+___=1800,那么AB ∥ CD
根据是_________________
(5)要使BE∥DF,必须∠1=___,
根据是_________________
三、解答题
16.如图,∠B=∠C,∠B+∠D=1800,那么BC平行于DE吗?为什么?
17.如图,AF,CE,BD交于点B,且BE平分∠DBF,且∠1=∠C,问BD与AC平行吗?为什么?
18.如图,AD平分∠BAC, EF平分∠DEC,且∠1=∠2,试说明DE与AB的位置关系。
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
C
D
C
D
C
A
A
A
A
C
二、填空题
11. ∠ABD=∠BDF(或∠CBD=∠BDE)
12.AC DE , DF BC
13.∠1 , ∠1 内错角相等,两直线平行
14.∠4 , ∠4 同旁内角互补,两直线平行
15.(1)AB CD 同位角相等,两直线平行(2)BE DF 同旁内角互补,两直线平行
(3)BE DF 内错角相等,两直线平行(4)∠2,同旁内角互补,两直线平行(5)∠D,同位角相等,两直线平行
16.解析:BC∥DE,理由如下:
∵∠B=∠C,∠B+∠D=1800,
∴∠C+∠D=1800,(等量代换)
∴BC∥DE(同旁内角互补,两直线平行)
17.解析:BD∥AC,理由 如下:
∵BE平分∠DBF,
∴∠1=∠EBD(角平分线定义)
∵∠1=∠C
∴∠C=∠EBD(等量代换)
∴BD∥AC(同位角相等,两直线平行)
18.
解析:DE∥AB,理由 如下:
∵AD平分∠BAC,(已知)
∴∠BAC=2∠1.(角平线的定义 )
∵EF平分∠DEC,(已知)
∴∠DEC=2∠2.(角平线的定义 )
∵∠1=∠2(已知)
∴∠BAC=∠DEC(等量代换)
∴DE∥AB(同位角相等,两直线平行)
