2020-2021学年苏科版七年级下册数学 第七章 平面的图形认识(二)解答题专项培优集训(二)(word版含解析)
文档属性
| 名称 | 2020-2021学年苏科版七年级下册数学 第七章 平面的图形认识(二)解答题专项培优集训(二)(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 218.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 07:01:59 | ||
图片预览



文档简介
苏科版七年级下册数学
第七章
平面的图形认识(二)
解答题专项培优集训(二)
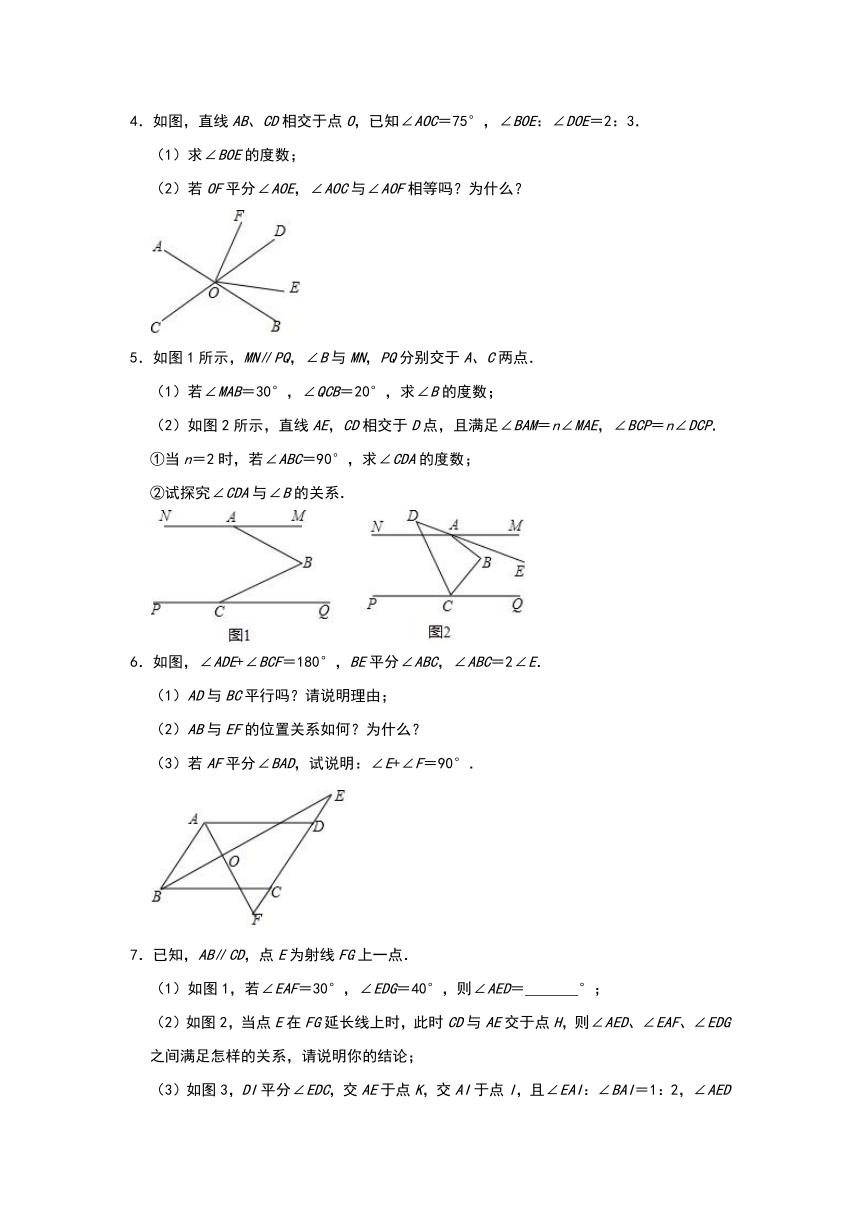
1.如图1,∠FBD=90°,EB=EF,CB=CD.
(1)求证:EF∥CD;
(2)如图2所示,若将△EBF沿射线BF平移,即EG∥BC,∠FBD=90°,EG=EF,CB=CD,请问(1)中的结论是否仍成立?请证明.
2.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
3.如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
(1)图中∠AOF的余角是
(把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据
可得∠BOD=
度;
(3)如果∠1=32°,求∠2和∠3的度数.
4.如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE:∠DOE=2:3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?
5.如图1所示,MN∥PQ,∠B与MN,PQ分别交于A、C两点.
(1)若∠MAB=30°,∠QCB=20°,求∠B的度数;
(2)如图2所示,直线AE,CD相交于D点,且满足∠BAM=n∠MAE,∠BCP=n∠DCP.
①当n=2时,若∠ABC=90°,求∠CDA的度数;
②试探究∠CDA与∠B的关系.
6.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:∠E+∠F=90°.
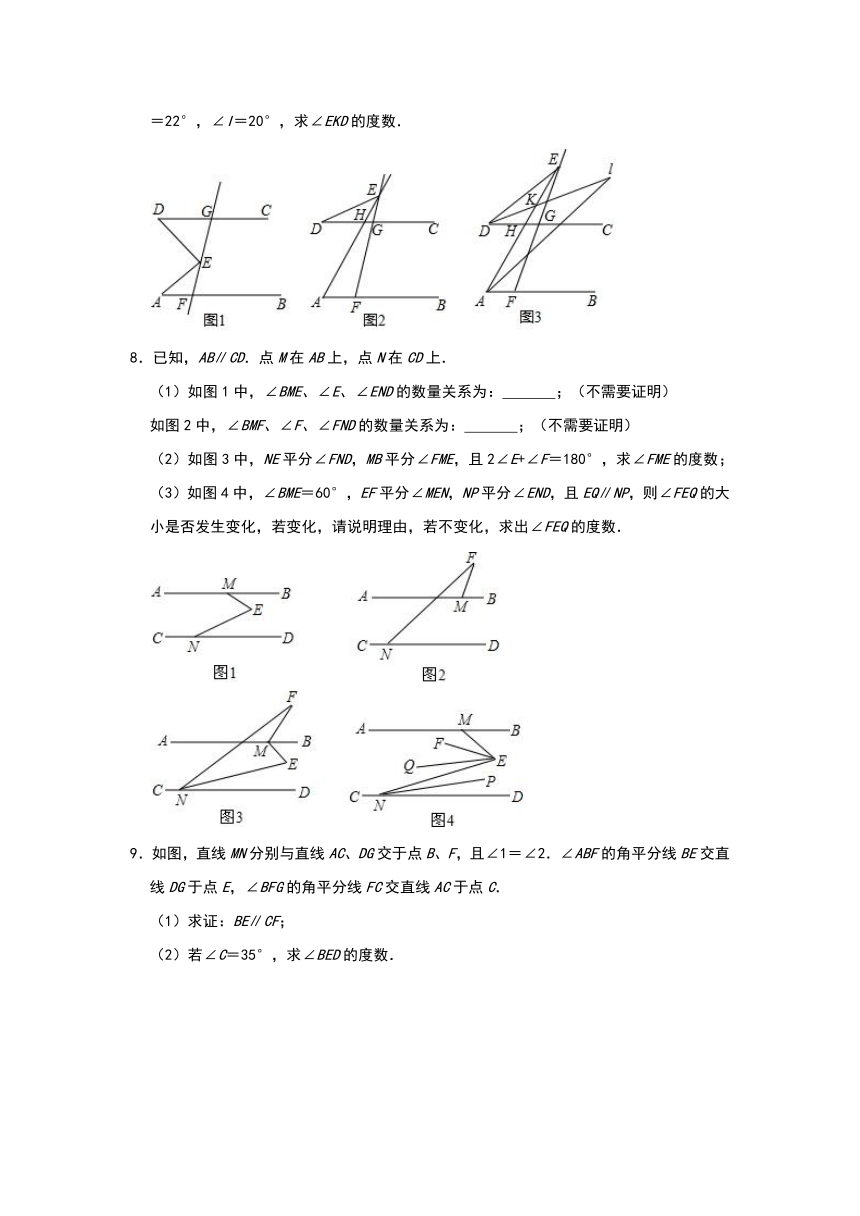
7.已知,AB∥CD,点E为射线FG上一点.
(1)如图1,若∠EAF=30°,∠EDG=40°,则∠AED=
°;
(2)如图2,当点E在FG延长线上时,此时CD与AE交于点H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;
(3)如图3,DI平分∠EDC,交AE于点K,交AI于点I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD的度数.
8.已知,AB∥CD.点M在AB上,点N在CD上.
(1)如图1中,∠BME、∠E、∠END的数量关系为:
;(不需要证明)
如图2中,∠BMF、∠F、∠FND的数量关系为:
;(不需要证明)
(2)如图3中,NE平分∠FND,MB平分∠FME,且2∠E+∠F=180°,求∠FME的度数;
(3)如图4中,∠BME=60°,EF平分∠MEN,NP平分∠END,且EQ∥NP,则∠FEQ的大小是否发生变化,若变化,请说明理由,若不变化,求出∠FEQ的度数.
9.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)求证:BE∥CF;
(2)若∠C=35°,求∠BED的度数.
10.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连接PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为
度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
11.如图1,已知直线CD∥EF,点A、B分别在直线CD与EF上.P为两平行线间一点.
(1)若∠DAP=40°,∠FBP=70°,则∠APB=
.
(2)猜想∠DAP,∠FBP,∠APB之间有什么关系?并说明理由.
(3)利用(2)的结论解答:
①如图2,AP1、BP1分别平分∠DAP、∠FBP,请你写出∠P与∠P1的数量关系,并说明理由.
②如图3,AP2、BP2分别平分∠CAP、∠EBP,若∠APB=β,求∠AP2B(用含β的代数式表示).
12.如图,已知直线AB,CD相交于点O,∠BOE=90°.
(1)若∠BOD=40°,求∠COE的度数;
(2)若∠AOC:∠BOC=3:7,求∠DOE的度数.
13.已知:
如图①,AB∥CD,∠1+∠3与∠2的关系是
;
如图②,AB∥CD,∠1+∠3+∠5与∠2+∠4的关系是
,证明你的结论.
说明理由:
如图③,AB∥CD,∠1+∠3+∠5+∠7与∠2+∠4+∠6的关系是
;
如图④,AB∥CD,∠1+∠3+∠5+…+∠(2n+1)与∠2+∠4+∠6+…+∠2n的关系.
14.已知,AB∥CD,CF平分∠ECD.
(1)如图1,若∠DCF=25°,∠E=20°,求∠ABE的度数.
(2)如图2,若∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,求∠ABE的度数.
(3)如图3,在(2)的条件下,P为射线BE上一点,H为CD上一点,PK平分∠BPH,HN∥PK,HM平分∠DHP,∠DHQ=2∠DHN,求∠PHQ的度数.
15.完成推理填空.
填写推理理由:
如图:EF∥AD,∠1=∠2,∠BAC=70°,把求∠AGD的过程填写完整.
∵EF∥AD,
∴∠2=
,(
)
又∵∠1=∠2,∴∠1=∠3,
∴AB∥
,(
)
∴∠BAC+
=180°,(
)
又∵∠BAC=70°,
∴∠AGD=110°.
参考答案
1.(1)证明:如图1,连接FD,
∵EB=EF,CB=CD,
∴∠EBF=∠EFB,∠CBD=∠CDB,
∵∠FBD=90°,
∴∠EBF+∠CBD=90°,∠BFD+∠BDF=90°,
∴∠EFB+∠CDB=90°,
∴∠EFD+∠CDF=180°,
∴EF∥CD;
(2)成立,
证明:如图2,连接FD,延长CB到H,
∵EG∥BC,
∴∠EGF=∠HBF,
∵∠FBD=90°,
∴∠HBF+∠CBD=90°,∠BFD+∠BDF=90°,
∴∠EGF+∠CBD=90°,
∵EG=EF,CB=CD,
∴∠EGF=∠EFB,∠CBD=∠CDB,
∴∠EFB+∠CDB=90°,
∴∠EFD+∠CDF=180°,
∴EF∥CD.
2.证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
3.解:(1)∵OF⊥OC,
∴∠COF=∠DOF=90°,
∴∠AOF+∠BOC=90°,∠AOF+∠AOD=90°,
∴∠AOF的余角是∠BOC、∠AOD;
故答案为:∠BOC、∠AOD;
(2)∵∠AOC=160°,
∴∠BOD=∠AOC=160°;
故答案为:对顶角相等;
160;
(3)∵OE平分∠AOD,
∴∠AOD=2∠1=64°,
∴∠2=∠AOD=64°,∠3=90°﹣64°=26°.
4.解:(1)设∠BOE=2x,则∠EOD=3x,
∠BOD=∠AOC=75°,
∴2x+3x=75°,
解得x=15°,
则2x=30°,
3x=45°,
∴∠BOE=30°;
(2)∵∠BOE=30°,
∴∠AOE=150°,
∵OF平分∠AOE,
∴∠AOF=75°,
∴∠AOC=∠AOF.
5.解:(1)如图1,过点B作BF∥MN,
则∠BAM=∠ABF=30°,
∵MN∥PQ,
∴PQ∥BF,
∴∠CBF=∠QCB=20°,
∴∠ABC=∠ABF+∠CBF=50°;
(2)①设∠MAE=x°,∠DCP=y°,
当n=2时,∠BAM=2x°,∠BCP=2y°,
∴∠BCQ=180°﹣2y°,
由(1)知,∠ABC=∠BAM+∠BCQ,
∴2x+180﹣2y=90,整理,得:x﹣y=﹣45,
如图2,延长DA交PQ于点G,
∵MN∥PQ,
∴∠MAE=∠DGC=x°,
则∠CDA=∠DCP﹣∠DGC
=y°﹣x°
=﹣(x﹣y)°
=45°;
②n∠CDA+∠ABC=180°,
设∠MAE=x°,∠DCP=y°,则∠BAM=n∠MAE=nx°,∠BCP=n∠DCP=ny°,
∴∠BCQ=180°﹣ny°,
由(1)知,∠ABC=nx°+180°﹣ny°,
∴y°﹣x°=,
∵MN∥PQ,
∴∠MAE=∠DGP=x°,
则∠CDA=∠DCP﹣∠DGC
=y°﹣x°
=,
即n∠CDA+∠ABC=180°.
6.解:(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=90°,
∴∠AOB=180°﹣90°=90°=∠EOF,
∴∠E+∠F=180°﹣∠EOF=90°.
7.解:(1)如图,延长DE交AB于H,
∵AB∥CD,
∴∠D=∠AHE=40°,
∵∠AED是△AEH的外角,
∴∠AED=∠A+∠AHE=30°+40°=70°,
故答案为:70;
(2)∠EAF=∠AED+∠EDG.
理由:∵AB∥CD,
∴∠EAF=∠EHC,
∵∠EHC是△DEH的外角,
∴∠EHG=∠AED+∠EDG,
∴∠EAF=∠AED+∠EDG;
(3)∵∠EAI:∠BAI=1:2,
∴设∠EAI=α,则∠BAE=3α,
∵∠AED=22°,∠I=20°,∠DKE=∠AKI,
又∵∠EDK+∠DKE+∠DEK=180°,∠KAI+∠KIA+∠AKI=180°,
∴∠EDK=α﹣2°,
∵DI平分∠EDC,
∴∠CDE=2∠EDK=2α﹣4°,
∵AB∥CD,
∴∠EHC=∠EAF=∠AED+∠EDG,
即3α=22°+2α﹣4°,
解得α=18°,
∴∠EDK=16°,
∴在△DKE中,∠EKD=180°﹣16°﹣22°=142°.
8.解:(1)过E作EH∥AB,如图1,
∴∠BME=∠MEH,
∵AB∥CD,
∴HE∥CD,
∴∠END=∠HEN,
∴∠MEN=∠MEH+∠HEN=∠BME+∠END,
即∠BME=∠MEN﹣∠END.
如图2,过F作FH∥AB,
∴∠BMF=∠MFK,
∵AB∥CD,
∴FH∥CD,
∴∠FND=∠KFN,
∴∠MFN=∠MFK﹣∠KFN=∠BMF﹣∠FND,
即:∠BMF=∠MFN+∠FND.
故答案为∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.
(2)由(1)得∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.
∵NE平分∠FND,MB平分∠FME,
∴∠FME=∠BME+∠BMF,∠FND=∠FNE+∠END,
∵2∠MEN+∠MFN=180°,
∴2(∠BME+∠END)+∠BMF﹣∠FND=180°,
∴2∠BME+2∠END+∠BMF﹣∠FND=180°,
即2∠BMF+∠FND+∠BMF﹣∠FND=180°,
解得∠BMF=60°,
∴∠FME=2∠BMF=120°;
(3)∠FEQ的大小没发生变化,∠FEQ=30°.
由(1)知:∠MEN=∠BME+∠END,
∵EF平分∠MEN,NP平分∠END,
∴∠FEN=∠MEN=(∠BME+∠END),∠ENP=∠END,
∵EQ∥NP,
∴∠NEQ=∠ENP,
∴∠FEQ=∠FEN﹣∠NEQ=(∠BME+∠END)﹣∠END=∠BME,
∵∠BME=60°,
∴∠FEQ=×60°=30°.
9.(1)证明:方法一:∵∠1=∠2,∠2=∠BFG,
∴∠1=∠BFG,
∴AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴∠EBF=∠ABF,BFG,
∴∠EBF=∠CFB,
∴BE∥CF;
方法二:∵∠1=∠2,∠1=∠ABF,∠2=∠BFG,
∴∠ABF=∠BFG,
∵∠ABF的平分线是BE,∠BFG的平分线是FC,
∴∠EBF=∠ABF,BFG,
∴∠EBF=∠CFB,
∴BE∥CF;
(2)解:∵AC∥DG,BE∥CF,∠C=35°,
∴∠C=∠CFG=35°,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
10.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
11.(1)证明:过P作PM∥CD,
∴∠APM=∠DAP.(两直线平行,内错角相等),
∵CD∥EF(已知),
∴PM∥CD(平行于同一条直线的两条直线互相平行),
∴∠MPB=∠FBP.(两直线平行,内错角相等),
∴∠APM+∠MPB=∠DAP+∠FBP.(等式性质)
即∠APB=∠DAP+∠FBP=40°+70°=110°.
(2)结论:∠APB=∠DAP+∠FBP.
理由:见(1)中证明.
(3)①结论:∠P=2∠P1;
理由:由(2)可知:∠P=∠DAP+∠FBP,∠P1=∠ADP1+∠FBP1,
∵∠DAP=2∠DAP1,∠FBP=2∠FBP1,
∴∠P=2∠P1.
②由①得∠APB=∠DAP+∠FBP,∠AP2B=∠CAP2+∠EBP2,
∵AP2、BP2分别平分∠CAP、∠EBP,
∴∠CAP2=∠CAP,∠EBP2=∠EBP,
∴∠AP2B=∠CAP+∠EBP,
=(180°﹣∠DAP)+(180°﹣∠FBP),
=180°﹣(∠DAP+∠FBP),
=180°﹣∠APB,
=180°﹣β.
12.解:(1)∵∠BOE=90°,∠BOD=40°,
∴∠AOE=90°,∠AOC=∠BOD=40°,
则∠COE=90°﹣40°=50°;
(2)∵∠AOC:∠BOC=3:7,
∴设∠AOC=3x,则∠BOC=7x,
∵∠AOC+∠BOC=180°,
∴3x+7x=180°,
解得:x=18°,
∴∠AOC=54°,
∵∠BOD=∠AOC,
∴∠BOD=54°,
∴∠DOE=∠BOE+∠BOD=90°+54°=144°.
13.解:如图①,AB∥CD,∠1+∠3与∠2的关系是∠2=∠1+∠3;
如图②,AB∥CD,∠1+∠3+∠5与∠2+∠4的关系是∠2+∠4=∠1+∠3+∠5,
证明:作EF∥AB,GH∥AB,MN∥AB,
∵AB∥CD,
∴AB∥EF∥GH∥DC∥MN,
∴∠1=∠BEF,∠FEM=∠EMN,∠NMG=∠MGH,∠HGD=∠5,
∵∠2=∠MEF+∠FEM,∠3=∠EMN+∠NMG,∠4=∠MGH+∠HGD,
∴∠2+∠4=∠MEF+∠FEM+∠MGH+∠HGD=∠BEF+∠EMN+∠NMG+∠HGD=∠1+∠3+∠5;
如图③,AB∥CD,∠1+∠3+∠5+∠7与∠2+∠4+∠6的关系是∠2+∠4+∠6=∠1+∠3+∠5+∠7;
如图④,AB∥CD,∠1+∠3+∠5+…+∠(2n+1)与∠2+∠4+∠6+…+∠2n的关系为:∠2+∠4+∠6+…+∠2n=∠1+∠3+∠5+…+∠(2n+1).
故答案为:∠2=∠1+∠3;∠2+∠4=∠1+∠3+∠5;∠2+∠4+∠6=∠1+∠3+∠5+∠7;∠2+∠4+∠6+…+∠2n=∠1+∠3+∠5+…+∠(2n+1)
14.解:(1)如图1,
过点E作ER∥AB,
∵AB∥CD,
∴ER∥CD,
∵∠DCF=25°,∠E=20°,
∵CF平分∠ECD,∴∠DCF=∠FCE=25°,
∴∠CER=∠DCE=2∠DCF=50°,
∴∠BER=∠CER﹣∠CEB=30°,
∴∠ABE=∠BER=30°
答:∠ABE的度数为30°.
(2)如图2,分别过点E、F作AB的平行线ET、FL,
∵∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,
设∠ABF=α,则∠EBF=2α,
∴∠ABE=3α,∴∠BET=∠ABE=3α,
设∠CEB=β,
则∠DCE=∠CET=∠CEB+∠BET=3α+β,
∵CF平分∠ECD,
∴∠DCF=∠FCE=,
∴∠CFL=,∠BFL=∠ABF=α,
∴∠CFB=∠CFL﹣∠BFL=,
∴2×+180﹣β=190,
∴α=10,
∴∠ABE=30°.
答:∠ABE的度数为30°.
(3)如图3,过点P作PJ∥AB,
∵AB∥CD,
∴PJ∥CD,
∵PK平分∠BPH,
∴∠KPH=∠KPB=x,
∵HN∥PK,
∴∠NHP=x,
设∠MHN=y,
∴∠MHP=x+y,
∵HM平分∠DHP,
∴∠DHM=∠MHP=x+y,
∵∠DHQ=2∠DHN,
∴∠DHQ=2(x+y+y)=2x+4y,
∴∠PHQ=∠DHQ﹣∠DHP=(2x+4y)﹣(2x+2y)=2y,
∴∠HPJ=∠DHP=2x+2y,
∴∠BPJ=∠ABE=30°=2y,
∴∠PHQ=30°
答:∠PHQ的度数为30°.
15.解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2,
∴∠1=∠3,
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补),
∵∠BAC=70°,
∴∠AGD=110°,
故答案为:∠3;两直线平行,同位角相等;DG;内错角相等,两直线平行;∠DGA;两直线平行,同旁内角互补.
第七章
平面的图形认识(二)
解答题专项培优集训(二)
1.如图1,∠FBD=90°,EB=EF,CB=CD.
(1)求证:EF∥CD;
(2)如图2所示,若将△EBF沿射线BF平移,即EG∥BC,∠FBD=90°,EG=EF,CB=CD,请问(1)中的结论是否仍成立?请证明.
2.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
3.如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
(1)图中∠AOF的余角是
(把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据
可得∠BOD=
度;
(3)如果∠1=32°,求∠2和∠3的度数.
4.如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE:∠DOE=2:3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?
5.如图1所示,MN∥PQ,∠B与MN,PQ分别交于A、C两点.
(1)若∠MAB=30°,∠QCB=20°,求∠B的度数;
(2)如图2所示,直线AE,CD相交于D点,且满足∠BAM=n∠MAE,∠BCP=n∠DCP.
①当n=2时,若∠ABC=90°,求∠CDA的度数;
②试探究∠CDA与∠B的关系.
6.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:∠E+∠F=90°.
7.已知,AB∥CD,点E为射线FG上一点.
(1)如图1,若∠EAF=30°,∠EDG=40°,则∠AED=
°;
(2)如图2,当点E在FG延长线上时,此时CD与AE交于点H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;
(3)如图3,DI平分∠EDC,交AE于点K,交AI于点I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD的度数.
8.已知,AB∥CD.点M在AB上,点N在CD上.
(1)如图1中,∠BME、∠E、∠END的数量关系为:
;(不需要证明)
如图2中,∠BMF、∠F、∠FND的数量关系为:
;(不需要证明)
(2)如图3中,NE平分∠FND,MB平分∠FME,且2∠E+∠F=180°,求∠FME的度数;
(3)如图4中,∠BME=60°,EF平分∠MEN,NP平分∠END,且EQ∥NP,则∠FEQ的大小是否发生变化,若变化,请说明理由,若不变化,求出∠FEQ的度数.
9.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)求证:BE∥CF;
(2)若∠C=35°,求∠BED的度数.
10.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连接PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为
度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
11.如图1,已知直线CD∥EF,点A、B分别在直线CD与EF上.P为两平行线间一点.
(1)若∠DAP=40°,∠FBP=70°,则∠APB=
.
(2)猜想∠DAP,∠FBP,∠APB之间有什么关系?并说明理由.
(3)利用(2)的结论解答:
①如图2,AP1、BP1分别平分∠DAP、∠FBP,请你写出∠P与∠P1的数量关系,并说明理由.
②如图3,AP2、BP2分别平分∠CAP、∠EBP,若∠APB=β,求∠AP2B(用含β的代数式表示).
12.如图,已知直线AB,CD相交于点O,∠BOE=90°.
(1)若∠BOD=40°,求∠COE的度数;
(2)若∠AOC:∠BOC=3:7,求∠DOE的度数.
13.已知:
如图①,AB∥CD,∠1+∠3与∠2的关系是
;
如图②,AB∥CD,∠1+∠3+∠5与∠2+∠4的关系是
,证明你的结论.
说明理由:
如图③,AB∥CD,∠1+∠3+∠5+∠7与∠2+∠4+∠6的关系是
;
如图④,AB∥CD,∠1+∠3+∠5+…+∠(2n+1)与∠2+∠4+∠6+…+∠2n的关系.
14.已知,AB∥CD,CF平分∠ECD.
(1)如图1,若∠DCF=25°,∠E=20°,求∠ABE的度数.
(2)如图2,若∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,求∠ABE的度数.
(3)如图3,在(2)的条件下,P为射线BE上一点,H为CD上一点,PK平分∠BPH,HN∥PK,HM平分∠DHP,∠DHQ=2∠DHN,求∠PHQ的度数.
15.完成推理填空.
填写推理理由:
如图:EF∥AD,∠1=∠2,∠BAC=70°,把求∠AGD的过程填写完整.
∵EF∥AD,
∴∠2=
,(
)
又∵∠1=∠2,∴∠1=∠3,
∴AB∥
,(
)
∴∠BAC+
=180°,(
)
又∵∠BAC=70°,
∴∠AGD=110°.
参考答案
1.(1)证明:如图1,连接FD,
∵EB=EF,CB=CD,
∴∠EBF=∠EFB,∠CBD=∠CDB,
∵∠FBD=90°,
∴∠EBF+∠CBD=90°,∠BFD+∠BDF=90°,
∴∠EFB+∠CDB=90°,
∴∠EFD+∠CDF=180°,
∴EF∥CD;
(2)成立,
证明:如图2,连接FD,延长CB到H,
∵EG∥BC,
∴∠EGF=∠HBF,
∵∠FBD=90°,
∴∠HBF+∠CBD=90°,∠BFD+∠BDF=90°,
∴∠EGF+∠CBD=90°,
∵EG=EF,CB=CD,
∴∠EGF=∠EFB,∠CBD=∠CDB,
∴∠EFB+∠CDB=90°,
∴∠EFD+∠CDF=180°,
∴EF∥CD.
2.证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
3.解:(1)∵OF⊥OC,
∴∠COF=∠DOF=90°,
∴∠AOF+∠BOC=90°,∠AOF+∠AOD=90°,
∴∠AOF的余角是∠BOC、∠AOD;
故答案为:∠BOC、∠AOD;
(2)∵∠AOC=160°,
∴∠BOD=∠AOC=160°;
故答案为:对顶角相等;
160;
(3)∵OE平分∠AOD,
∴∠AOD=2∠1=64°,
∴∠2=∠AOD=64°,∠3=90°﹣64°=26°.
4.解:(1)设∠BOE=2x,则∠EOD=3x,
∠BOD=∠AOC=75°,
∴2x+3x=75°,
解得x=15°,
则2x=30°,
3x=45°,
∴∠BOE=30°;
(2)∵∠BOE=30°,
∴∠AOE=150°,
∵OF平分∠AOE,
∴∠AOF=75°,
∴∠AOC=∠AOF.
5.解:(1)如图1,过点B作BF∥MN,
则∠BAM=∠ABF=30°,
∵MN∥PQ,
∴PQ∥BF,
∴∠CBF=∠QCB=20°,
∴∠ABC=∠ABF+∠CBF=50°;
(2)①设∠MAE=x°,∠DCP=y°,
当n=2时,∠BAM=2x°,∠BCP=2y°,
∴∠BCQ=180°﹣2y°,
由(1)知,∠ABC=∠BAM+∠BCQ,
∴2x+180﹣2y=90,整理,得:x﹣y=﹣45,
如图2,延长DA交PQ于点G,
∵MN∥PQ,
∴∠MAE=∠DGC=x°,
则∠CDA=∠DCP﹣∠DGC
=y°﹣x°
=﹣(x﹣y)°
=45°;
②n∠CDA+∠ABC=180°,
设∠MAE=x°,∠DCP=y°,则∠BAM=n∠MAE=nx°,∠BCP=n∠DCP=ny°,
∴∠BCQ=180°﹣ny°,
由(1)知,∠ABC=nx°+180°﹣ny°,
∴y°﹣x°=,
∵MN∥PQ,
∴∠MAE=∠DGP=x°,
则∠CDA=∠DCP﹣∠DGC
=y°﹣x°
=,
即n∠CDA+∠ABC=180°.
6.解:(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=90°,
∴∠AOB=180°﹣90°=90°=∠EOF,
∴∠E+∠F=180°﹣∠EOF=90°.
7.解:(1)如图,延长DE交AB于H,
∵AB∥CD,
∴∠D=∠AHE=40°,
∵∠AED是△AEH的外角,
∴∠AED=∠A+∠AHE=30°+40°=70°,
故答案为:70;
(2)∠EAF=∠AED+∠EDG.
理由:∵AB∥CD,
∴∠EAF=∠EHC,
∵∠EHC是△DEH的外角,
∴∠EHG=∠AED+∠EDG,
∴∠EAF=∠AED+∠EDG;
(3)∵∠EAI:∠BAI=1:2,
∴设∠EAI=α,则∠BAE=3α,
∵∠AED=22°,∠I=20°,∠DKE=∠AKI,
又∵∠EDK+∠DKE+∠DEK=180°,∠KAI+∠KIA+∠AKI=180°,
∴∠EDK=α﹣2°,
∵DI平分∠EDC,
∴∠CDE=2∠EDK=2α﹣4°,
∵AB∥CD,
∴∠EHC=∠EAF=∠AED+∠EDG,
即3α=22°+2α﹣4°,
解得α=18°,
∴∠EDK=16°,
∴在△DKE中,∠EKD=180°﹣16°﹣22°=142°.
8.解:(1)过E作EH∥AB,如图1,
∴∠BME=∠MEH,
∵AB∥CD,
∴HE∥CD,
∴∠END=∠HEN,
∴∠MEN=∠MEH+∠HEN=∠BME+∠END,
即∠BME=∠MEN﹣∠END.
如图2,过F作FH∥AB,
∴∠BMF=∠MFK,
∵AB∥CD,
∴FH∥CD,
∴∠FND=∠KFN,
∴∠MFN=∠MFK﹣∠KFN=∠BMF﹣∠FND,
即:∠BMF=∠MFN+∠FND.
故答案为∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.
(2)由(1)得∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.
∵NE平分∠FND,MB平分∠FME,
∴∠FME=∠BME+∠BMF,∠FND=∠FNE+∠END,
∵2∠MEN+∠MFN=180°,
∴2(∠BME+∠END)+∠BMF﹣∠FND=180°,
∴2∠BME+2∠END+∠BMF﹣∠FND=180°,
即2∠BMF+∠FND+∠BMF﹣∠FND=180°,
解得∠BMF=60°,
∴∠FME=2∠BMF=120°;
(3)∠FEQ的大小没发生变化,∠FEQ=30°.
由(1)知:∠MEN=∠BME+∠END,
∵EF平分∠MEN,NP平分∠END,
∴∠FEN=∠MEN=(∠BME+∠END),∠ENP=∠END,
∵EQ∥NP,
∴∠NEQ=∠ENP,
∴∠FEQ=∠FEN﹣∠NEQ=(∠BME+∠END)﹣∠END=∠BME,
∵∠BME=60°,
∴∠FEQ=×60°=30°.
9.(1)证明:方法一:∵∠1=∠2,∠2=∠BFG,
∴∠1=∠BFG,
∴AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴∠EBF=∠ABF,BFG,
∴∠EBF=∠CFB,
∴BE∥CF;
方法二:∵∠1=∠2,∠1=∠ABF,∠2=∠BFG,
∴∠ABF=∠BFG,
∵∠ABF的平分线是BE,∠BFG的平分线是FC,
∴∠EBF=∠ABF,BFG,
∴∠EBF=∠CFB,
∴BE∥CF;
(2)解:∵AC∥DG,BE∥CF,∠C=35°,
∴∠C=∠CFG=35°,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
10.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
11.(1)证明:过P作PM∥CD,
∴∠APM=∠DAP.(两直线平行,内错角相等),
∵CD∥EF(已知),
∴PM∥CD(平行于同一条直线的两条直线互相平行),
∴∠MPB=∠FBP.(两直线平行,内错角相等),
∴∠APM+∠MPB=∠DAP+∠FBP.(等式性质)
即∠APB=∠DAP+∠FBP=40°+70°=110°.
(2)结论:∠APB=∠DAP+∠FBP.
理由:见(1)中证明.
(3)①结论:∠P=2∠P1;
理由:由(2)可知:∠P=∠DAP+∠FBP,∠P1=∠ADP1+∠FBP1,
∵∠DAP=2∠DAP1,∠FBP=2∠FBP1,
∴∠P=2∠P1.
②由①得∠APB=∠DAP+∠FBP,∠AP2B=∠CAP2+∠EBP2,
∵AP2、BP2分别平分∠CAP、∠EBP,
∴∠CAP2=∠CAP,∠EBP2=∠EBP,
∴∠AP2B=∠CAP+∠EBP,
=(180°﹣∠DAP)+(180°﹣∠FBP),
=180°﹣(∠DAP+∠FBP),
=180°﹣∠APB,
=180°﹣β.
12.解:(1)∵∠BOE=90°,∠BOD=40°,
∴∠AOE=90°,∠AOC=∠BOD=40°,
则∠COE=90°﹣40°=50°;
(2)∵∠AOC:∠BOC=3:7,
∴设∠AOC=3x,则∠BOC=7x,
∵∠AOC+∠BOC=180°,
∴3x+7x=180°,
解得:x=18°,
∴∠AOC=54°,
∵∠BOD=∠AOC,
∴∠BOD=54°,
∴∠DOE=∠BOE+∠BOD=90°+54°=144°.
13.解:如图①,AB∥CD,∠1+∠3与∠2的关系是∠2=∠1+∠3;
如图②,AB∥CD,∠1+∠3+∠5与∠2+∠4的关系是∠2+∠4=∠1+∠3+∠5,
证明:作EF∥AB,GH∥AB,MN∥AB,
∵AB∥CD,
∴AB∥EF∥GH∥DC∥MN,
∴∠1=∠BEF,∠FEM=∠EMN,∠NMG=∠MGH,∠HGD=∠5,
∵∠2=∠MEF+∠FEM,∠3=∠EMN+∠NMG,∠4=∠MGH+∠HGD,
∴∠2+∠4=∠MEF+∠FEM+∠MGH+∠HGD=∠BEF+∠EMN+∠NMG+∠HGD=∠1+∠3+∠5;
如图③,AB∥CD,∠1+∠3+∠5+∠7与∠2+∠4+∠6的关系是∠2+∠4+∠6=∠1+∠3+∠5+∠7;
如图④,AB∥CD,∠1+∠3+∠5+…+∠(2n+1)与∠2+∠4+∠6+…+∠2n的关系为:∠2+∠4+∠6+…+∠2n=∠1+∠3+∠5+…+∠(2n+1).
故答案为:∠2=∠1+∠3;∠2+∠4=∠1+∠3+∠5;∠2+∠4+∠6=∠1+∠3+∠5+∠7;∠2+∠4+∠6+…+∠2n=∠1+∠3+∠5+…+∠(2n+1)
14.解:(1)如图1,
过点E作ER∥AB,
∵AB∥CD,
∴ER∥CD,
∵∠DCF=25°,∠E=20°,
∵CF平分∠ECD,∴∠DCF=∠FCE=25°,
∴∠CER=∠DCE=2∠DCF=50°,
∴∠BER=∠CER﹣∠CEB=30°,
∴∠ABE=∠BER=30°
答:∠ABE的度数为30°.
(2)如图2,分别过点E、F作AB的平行线ET、FL,
∵∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,
设∠ABF=α,则∠EBF=2α,
∴∠ABE=3α,∴∠BET=∠ABE=3α,
设∠CEB=β,
则∠DCE=∠CET=∠CEB+∠BET=3α+β,
∵CF平分∠ECD,
∴∠DCF=∠FCE=,
∴∠CFL=,∠BFL=∠ABF=α,
∴∠CFB=∠CFL﹣∠BFL=,
∴2×+180﹣β=190,
∴α=10,
∴∠ABE=30°.
答:∠ABE的度数为30°.
(3)如图3,过点P作PJ∥AB,
∵AB∥CD,
∴PJ∥CD,
∵PK平分∠BPH,
∴∠KPH=∠KPB=x,
∵HN∥PK,
∴∠NHP=x,
设∠MHN=y,
∴∠MHP=x+y,
∵HM平分∠DHP,
∴∠DHM=∠MHP=x+y,
∵∠DHQ=2∠DHN,
∴∠DHQ=2(x+y+y)=2x+4y,
∴∠PHQ=∠DHQ﹣∠DHP=(2x+4y)﹣(2x+2y)=2y,
∴∠HPJ=∠DHP=2x+2y,
∴∠BPJ=∠ABE=30°=2y,
∴∠PHQ=30°
答:∠PHQ的度数为30°.
15.解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2,
∴∠1=∠3,
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补),
∵∠BAC=70°,
∴∠AGD=110°,
故答案为:∠3;两直线平行,同位角相等;DG;内错角相等,两直线平行;∠DGA;两直线平行,同旁内角互补.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
