第二十章 数据的分析单元卷(Word版 含答案)
文档属性
| 名称 | 第二十章 数据的分析单元卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 482.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 21:05:05 | ||
图片预览



文档简介
第二十章 数据的分析
一、单选题(将唯一正确答案的代号填在题后括号内,每题3分,共30分)
1.小华在一次射击训练时,连续10次的成绩为3次10环、2次9环、5次8环,则小华这10次射击的平均成绩为( )
A.8.6环 B.8.7 环 C.8.8 环 D.8.9环
2.一组数据2、3、4、6、6、7的众数是( )
A.3 B.4 C.5 D.6
3.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩都为9环,方差分别为S甲2=0.56,S乙2=0.62,S丙2=0.39,S丁2=0.42,则四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
4.某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行考核(考核的满分均为100分),三个方面的重要性之比依次为3︰5︰2,小王经过考核后所得的分数依次为90、88、83分,那么小王的最后得分是( )
A.87 B.87.6 C.87.8 D.88
5.数据10,10,x,8的众数与平均数相同,那么这组数的中位数是( )
A.10 B.8 C.12 D.4
6.某校要从四名学生中选拔一名参加市风华小主播大赛,在校的挑战赛中,四名学生的平均成绩x和方差如表所示,如果要选一名成绩高且发挥稳定的学生参赛,那么应选的学生是( )
A.甲 B.乙 C.丙 D.丁
7.某市初中毕业生进行了一项技能测试,有4万名考生的得分都是不小于70的两位数,从中随机抽取4000个数据,统计如下表:
数据x 70≤x≤79 80≤x≤89 90≤x≤99
个数 800 2000 1200
平均数 78 85 92
请根据表格中的信息,估计这4万个数据的平均数约为( )
A.92.1 B.85.7 C.83.4 D.78.8
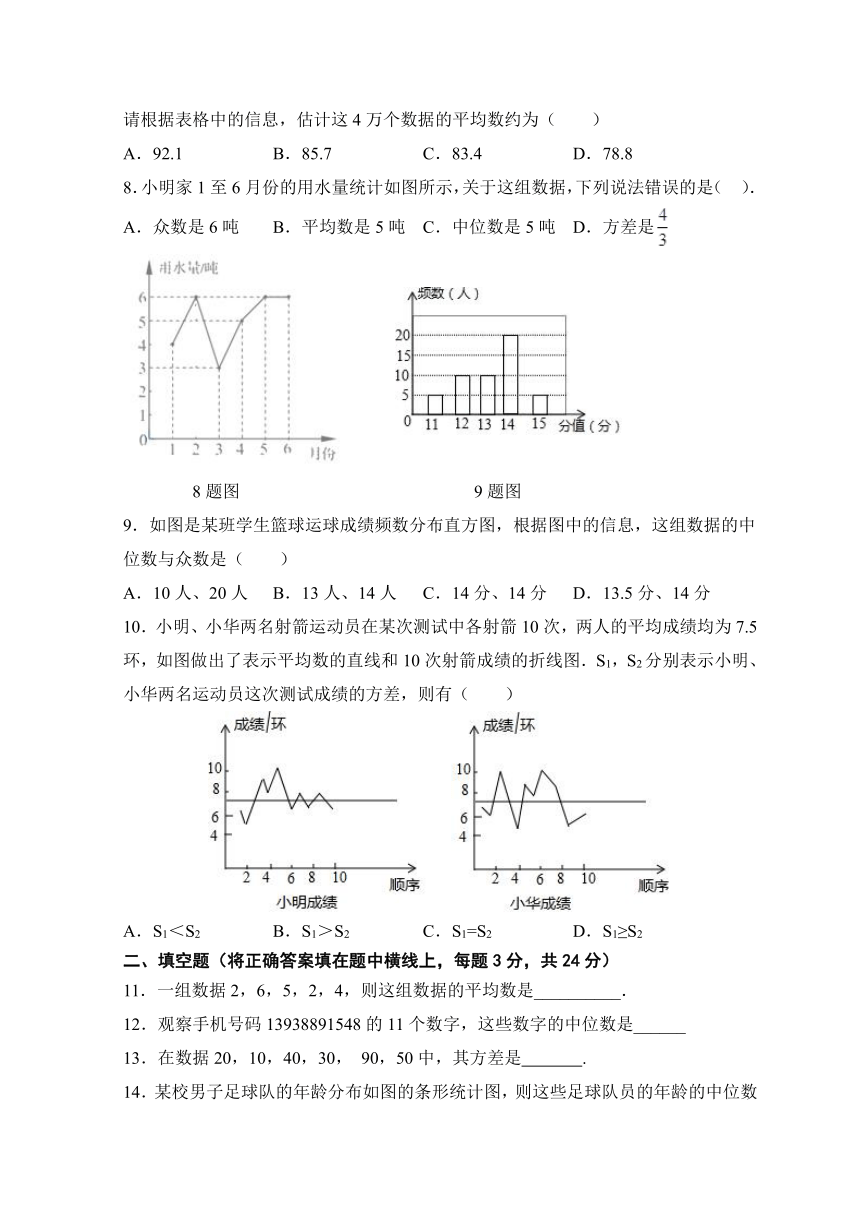
8.小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
A.众数是6吨 B.平均数是5吨 C.中位数是5吨 D.方差是
8题图 9题图
9.如图是某班学生篮球运球成绩频数分布直方图,根据图中的信息,这组数据的中位数与众数是( )
A.10人、20人 B.13人、14人 C.14分、14分 D.13.5分、14分
10.小明、小华两名射箭运动员在某次测试中各射箭10次,两人的平均成绩均为7.5环,如图做出了表示平均数的直线和10次射箭成绩的折线图.S1,S2分别表示小明、小华两名运动员这次测试成绩的方差,则有( )
A.S1<S2 B.S1>S2 C.S1=S2 D.S1≥S2
二、填空题(将正确答案填在题中横线上,每题3分,共24分)
11.一组数据2,6,5,2,4,则这组数据的平均数是__________.
12.观察手机号码13938891548的11个数字,这些数字的中位数是______
13.在数据20,10,40,30, 90,50中,其方差是 .
14.某校男子足球队的年龄分布如图的条形统计图,则这些足球队员的年龄的中位数是_______岁.
15.某“中学生暑期环保小组”的同学,随机调查了“金沙绿岛”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9,利用上述数据估计该小区500户家庭一周内需要环保方便袋__________只.
16.若一组数据3,3,4,x,8的平均数是4,则这组数据的中位数是___________.
17.两组数据m,6,n与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组新数据的中位数为_____.
18.已知点(x1,y1),(x2,y2),(x3,y3)都在函数y=-2x+7的图象上,若数据x1,x2,x3的方差为5,则另一组数据y1,y2,y3的方差为_________.
三、解答题(本题共有8小题,共66分)
19.(本题8分)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,然后再按笔试占60%、面试占40%计算候选人的综合成绩.他们的各项成绩如下表所示:
候选人 笔试成绩(分) 面试成绩(分)
甲 90 88
乙 84 92
丙 a 90
丁 88 86
(1)现得知候选人丙的综合成绩为87.6分,求表中a的值
(2)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
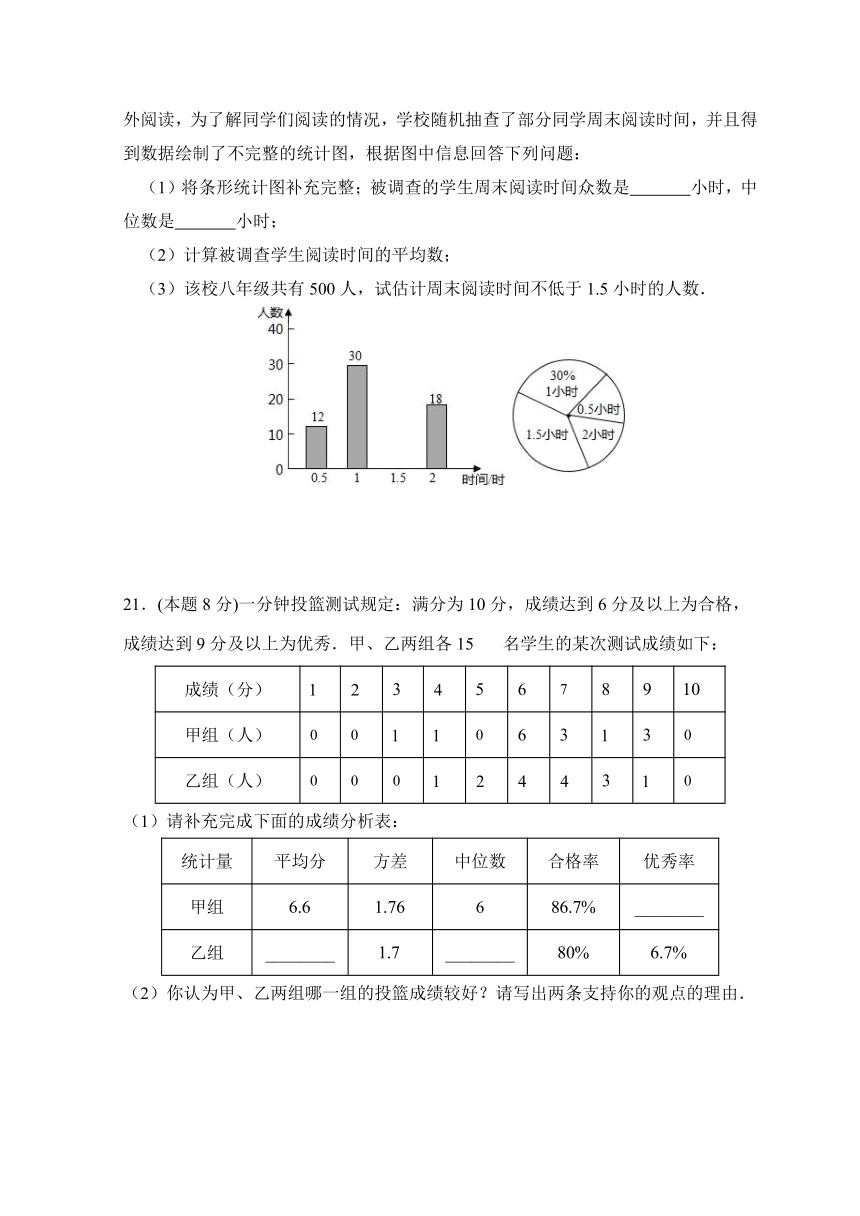
20.(本题8分)为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是 小时,中位数是 小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
21.(本题8分)一分钟投篮测试规定:满分为10分,成绩达到6分及以上为合格,成绩达到9分及以上为优秀.甲、乙两组各15名学生的某次测试成绩如下:
成绩(分)
甲组(人)
乙组(人)
(1)请补充完成下面的成绩分析表:
统计量 平均分 方差 中位数 合格率 优秀率
甲组
________
乙组 ________
________
(2)你认为甲、乙两组哪一组的投篮成绩较好?请写出两条支持你的观点的理由.
22.(本题8分)我市某校招聘数学教师,本次招聘进行专业技能笔试和课堂教学展示两个项目的考核,这两项考核的满分均为100分,学校将这两个项目的得分按一定的比例计算出总成绩.经统计,参加考核的4名考生的两个项目的得分如下:
考生序号 1 2 3 4
专业技能笔试 90 70 86 75
课堂教学展示 70 90 80 86
(1)经过计算,1号考生的总成绩为78分,求专业技能笔试得分和课堂教学展示得分分别占总成绩的百分比;
(2)若学校录取总成绩最高的考生,通过计算说明4名考生中哪一名考生会被录取?
23.(本题8分)某校八年级两个班,各选派10名学生参加学校举行的“美丽家乡风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 最高分 平均分 中位数 众数 方差
八(1)班 100 m 93 93 12
八(2)班 99 95 n 93 8.4
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好,请您写出两条支持八(2)班成绩好的理由.
24.(本题8分)某校德育处组织“四品八德”好少年评比活动,每班只有一个名额.现某班有甲、乙、丙三名学生参与竞选,第一轮根据“品行规范”、“学习规范”进行量化考核.甲、乙、丙他们的量化考核成绩(单位:分)分别用两种方式进行了统计,如下表和图1:
(1)请将表和图1中的空缺部分补充完整;
(2)竞选的第二轮是由本班的50位学生进行投票,每票计6分,甲、乙、丙三人的得票情况如图2(没有弃权票,每名学生只能选一人).
①若将“品行规范”、“学习规范”、“得票”三项测试得分按4:3:3的比例确定最后成绩,通过计算谁将会被推选为校“四品八德”好少年.
②若规定得票测试分占20%,要使甲学生最后得分不低于91分,则“品行规范”成绩在总分中所占比例的取值范围应是 .
25.(本题8分)某校八年级(1)班积极响应学校团委的号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐图书400册.特别值得一提的是李保、王刚两位同学在父母的支持下各捐献了90册图书.班长统计了全班捐书情况如下表(被粗心的马小虎用墨水污染了一部分):
册数 4 5 6 7 8 90
人数 6 8 15
2
(1)分别求出该班级捐献7册图书和8册图书的人数;
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪个统计量不能反映该班同学捐书册数的一般状况,说明理由.
26.(本题10分)某厂生产A、B两种产品.其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
A、B产品单价变化统计表
第一次 第二次 第三次
A产品单价(元/件) 6 5.2 6.5
B产品单价(元/件) 3.5 4 3
并求得A产品三次单价的平均数和方差:
:.
(1)补全图中B产品单价变化的折线图.B产品第三次的单价比上一次的单价降低了____%;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小:
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1.求m的值.
参考答案
1.C. 解析:=8.8(环),
故小华这10次射击的平均成绩为8.8环,故选:C.
2.D. 解析:6出现了2次,出现的次数最多,则众数是6;故选:D.
3.C. 解析:∵方差越小数据组中的数据越稳定,而四名同学这10射击的方差中,最小的是S丙2=0.39,∴这四人中丙的成绩最稳定. 故选C.
4.B. 解析:根据题意,有:
小王的最后得分为:;故选:B.
5.A. 解析:根据众数和平均数相等列方程.要分类讨论.
(1)当众数为10时,根据题意得:10+10+x+8=4×10,解得x=12,
则中位数是10;
(2)当x=8时,有两个众数,而平均数为(10×2+8×2)÷4=9,不合题意.
故选A.
6.C. 解析:∵9>8,∴乙、丙两名学生的平均成绩高于甲、丁两名学生,
又∵1<1.2,∴丙的方差小于乙的方差,∴丙发挥稳定,
∴要选一名成绩高且发挥稳定的学生参赛,则应选择的学生是丙.
故选:C.
7.B. 解析:由表可知,样本的平均数为
则估计这4万个数据的平均数约为
故选:B.
8.C. 解析:根据众数、平均数、中位数、方差:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
数据:3,4,5,6,6,6的众数是6,平均数是5,中位数是5.5,方差是,
所以,选项A、B、D正确,选项C错误,故选C.
9.D. 解析:由频数分布图可知,11分的有5人,12分的有10人,13分的有10人,14分的有20人,15分的有5个,所以共有50人,篮球运球成绩在第25位的是13分,在第26位的是14分,所以中位数是(13+14)÷2=13.5,14分的人数最多,所以众数是14,故选D.
10.A. 解析:根据图形可得,小明、小华两名射箭运动员在某次测试中各射箭10次所得的成绩中,小明的成绩与平均成绩离散程度小,而小华的成绩与平均成绩离散程度大,故S1<S2,故选:A.
11.. 解析:这组数据的平均数,故答案为:.
12.5. 解析:中位数的求法:把一组数据按从小到大的顺序排列,最中间的一个数或中间两个数的平均数就是这组数据的平均数. 把手机号码13938891548的11个数字按从小到大的顺序排列为11334588899,则这组数据的中位数为5.
13.. 解析:先计算平均数:(20+10+40+30+90+50)÷6=40,
方差为:S2=[(20-40)2+(10-40)2+(40-40)2+(30-40)2+(90-40)2+(50-40)2]
==,故方差为.
14.15. 解析:根据图示可得,共有:8+10+4+2=24(人),
中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)因此这些足球队员的年龄的中位数是第12名和第13名的平均年龄,为:15.
15.3500. 解析:由10户家庭一周内使用环保方便袋的数量可知,平均每户一周使用的环保方便袋的数量为,
则该小区500户家庭一周内需要环保方便袋约为,
故答案为3500.
16.3. 解析:由题意可知,(3+3+4+x+8)÷5=4,解得x=2,
这组数据从小到大排列2,3,3,4,8,
所以中位数是3.
17.7. 解析:∵组数据m,6,n与1,m,2n,7的平均数都是6,
∴,解得:,若将这两组数据合并为一组数据,按从小到大的顺序排列为1,4,6,7,8,8,8,一共7个数,第四个数是7,则这组数据的中位数是7;故答案为7.
18.20.解析:设这组数据x1,x2,x3的平均数为,
则另一组新数据-2x1+7,-2x2+7,-2x3+7的平均数为-2+7,
∵S2=[(x1-)2+(x2-)2+(x3-)2]=5,
∴方差为S′2= [(-2x1+7+2-7)2+(-2x2+7+2-7)2+(-2x3+7+2-7)2]
= [4(x1-)2+4(x2-)2+4(x3-)2]
=4S2
=4×5
=20,
故答案为:20.
19.解:(1)由题意得:,解得:
答:表中a的值为86
(2)甲候选人的综合成绩为:(分);
乙候选人的综合成绩为:(分);
丁候选人的综合成绩为:(分);
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙
20.解:(1)由题意可得,本次调查的学生数为:30÷30%=100,
阅读时间1.5小时的学生数为:100﹣12﹣30﹣18=40,
补全的条形统计图如图所示,
由补全的条形统计图可知,被调查的学生周末阅读时间众数是1.5小时,中位数是1.5小时,
故答案为1.5,1.5;
(2)所有被调查学生阅读时间的平均数为:×(12×0.5+30×1+40×1.5+18×2)=1.32小时,
即所有被调查同学的平均阅读时间为1.32小时.
(3)估计周末阅读时间不低于1.5小时的人数为500×=290(人).
21.解:(1)乙组的平均分是:(4×1+5×2+6×4+7×4+8×3+9×1)÷15=6.6;
把乙组的数据从小到大排列,最中间的数是第8个数,是7;则中位数是7,
∵成绩达到9分及以上为优秀,
∴甲组的优秀率是×100%=20%;
填表如下:
统计量 平均分 方差 中位数 合格率 优秀率
甲组
20%
乙组 6.6
7
(2)认为甲组的投篮成绩较好,理由如下:
①甲组成绩的合格率比乙组的高;②甲组成绩的优秀率比乙组的高.?
认为乙组的投篮成绩较好,理由如下:
①乙组成绩的中位数比甲组的高;②乙组成绩的方差比甲组的小.
22.解:(1)设专业技能笔试得分占总成绩的百分比是a.
根据题意,得90a+70(1-a)=78.
解这个方程,得a=40%.1-40%=60%.
所以专业技能笔试和课堂教学展示得分占总成绩的百分比分别是40%,60%.
(2)2号考生总成绩为70×0.4+90×0.6=82(分).
3号考生总成绩为86×0.4+80×0.6=82.4(分).
4号考生总成绩为75×0.4+86×0.6=81.6(分).
因为82.4>82>81.6>78,所以3号考生会被录取.
23.解:(1)八(1)班的平均分m=×(88+91+92+93+93+93+94+98+98+100)=94;八(2)班的中位数n==95.5; ∴m=94, n=95.5 .
(2)八(2)班的平均分高于八(1)班;八(2)班的成绩集中在中上游,故支持八(2)班成绩好.
24.解:(1)由统计表可知,乙的学习规范分数85;
(2)解:① 甲得票分,
乙得票分,
丙得票分,
分 ,
分 ,
分 ,
所以乙将被推荐为校“四品八德”好少年;
②设品行规范成绩在总分中所占比例为x,则学习规范在总分中所占比例为(1-0.2- x),根据题意,得,95×x+80×(1-0.2- x)+90×20%≥91,
化简,得15x≥9,解得x≥0.6,1-0.2- x>0,∴x<0.8.
故取值范围:
25.解:(1)设捐7册图书的有x人,捐8册图书的有y人.
则根据题意列出方程:
解得:
捐7册图书的有6人,捐8册图书的有3人.
(2)平均数是10册,中位数是6册,众数是6册.其中平均数10册不能反映该班同学捐书册数的一般情况,因为40名同学中,有38名同学的捐书册数都没有达到10册,平均数主要受到捐书90册的2位同学的捐书册数的影响,故而不能反映该班同学捐书册数的一般情况.
26.解:(1)如图所示
A、B产品单价变化的折线图,如上图.
即:B产品第三次的单价比上一次的单价降低了25%.
(2),
.
∵,∴B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为;
对于B产品,∵m>0,∴第四次单价大于3.
又∵,∴第四次单价小于4.
∴,∴m=25.
一、单选题(将唯一正确答案的代号填在题后括号内,每题3分,共30分)
1.小华在一次射击训练时,连续10次的成绩为3次10环、2次9环、5次8环,则小华这10次射击的平均成绩为( )
A.8.6环 B.8.7 环 C.8.8 环 D.8.9环
2.一组数据2、3、4、6、6、7的众数是( )
A.3 B.4 C.5 D.6
3.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩都为9环,方差分别为S甲2=0.56,S乙2=0.62,S丙2=0.39,S丁2=0.42,则四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
4.某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行考核(考核的满分均为100分),三个方面的重要性之比依次为3︰5︰2,小王经过考核后所得的分数依次为90、88、83分,那么小王的最后得分是( )
A.87 B.87.6 C.87.8 D.88
5.数据10,10,x,8的众数与平均数相同,那么这组数的中位数是( )
A.10 B.8 C.12 D.4
6.某校要从四名学生中选拔一名参加市风华小主播大赛,在校的挑战赛中,四名学生的平均成绩x和方差如表所示,如果要选一名成绩高且发挥稳定的学生参赛,那么应选的学生是( )
A.甲 B.乙 C.丙 D.丁
7.某市初中毕业生进行了一项技能测试,有4万名考生的得分都是不小于70的两位数,从中随机抽取4000个数据,统计如下表:
数据x 70≤x≤79 80≤x≤89 90≤x≤99
个数 800 2000 1200
平均数 78 85 92
请根据表格中的信息,估计这4万个数据的平均数约为( )
A.92.1 B.85.7 C.83.4 D.78.8
8.小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
A.众数是6吨 B.平均数是5吨 C.中位数是5吨 D.方差是
8题图 9题图
9.如图是某班学生篮球运球成绩频数分布直方图,根据图中的信息,这组数据的中位数与众数是( )
A.10人、20人 B.13人、14人 C.14分、14分 D.13.5分、14分
10.小明、小华两名射箭运动员在某次测试中各射箭10次,两人的平均成绩均为7.5环,如图做出了表示平均数的直线和10次射箭成绩的折线图.S1,S2分别表示小明、小华两名运动员这次测试成绩的方差,则有( )
A.S1<S2 B.S1>S2 C.S1=S2 D.S1≥S2
二、填空题(将正确答案填在题中横线上,每题3分,共24分)
11.一组数据2,6,5,2,4,则这组数据的平均数是__________.
12.观察手机号码13938891548的11个数字,这些数字的中位数是______
13.在数据20,10,40,30, 90,50中,其方差是 .
14.某校男子足球队的年龄分布如图的条形统计图,则这些足球队员的年龄的中位数是_______岁.
15.某“中学生暑期环保小组”的同学,随机调查了“金沙绿岛”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9,利用上述数据估计该小区500户家庭一周内需要环保方便袋__________只.
16.若一组数据3,3,4,x,8的平均数是4,则这组数据的中位数是___________.
17.两组数据m,6,n与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组新数据的中位数为_____.
18.已知点(x1,y1),(x2,y2),(x3,y3)都在函数y=-2x+7的图象上,若数据x1,x2,x3的方差为5,则另一组数据y1,y2,y3的方差为_________.
三、解答题(本题共有8小题,共66分)
19.(本题8分)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,然后再按笔试占60%、面试占40%计算候选人的综合成绩.他们的各项成绩如下表所示:
候选人 笔试成绩(分) 面试成绩(分)
甲 90 88
乙 84 92
丙 a 90
丁 88 86
(1)现得知候选人丙的综合成绩为87.6分,求表中a的值
(2)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
20.(本题8分)为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是 小时,中位数是 小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
21.(本题8分)一分钟投篮测试规定:满分为10分,成绩达到6分及以上为合格,成绩达到9分及以上为优秀.甲、乙两组各15名学生的某次测试成绩如下:
成绩(分)
甲组(人)
乙组(人)
(1)请补充完成下面的成绩分析表:
统计量 平均分 方差 中位数 合格率 优秀率
甲组
________
乙组 ________
________
(2)你认为甲、乙两组哪一组的投篮成绩较好?请写出两条支持你的观点的理由.
22.(本题8分)我市某校招聘数学教师,本次招聘进行专业技能笔试和课堂教学展示两个项目的考核,这两项考核的满分均为100分,学校将这两个项目的得分按一定的比例计算出总成绩.经统计,参加考核的4名考生的两个项目的得分如下:
考生序号 1 2 3 4
专业技能笔试 90 70 86 75
课堂教学展示 70 90 80 86
(1)经过计算,1号考生的总成绩为78分,求专业技能笔试得分和课堂教学展示得分分别占总成绩的百分比;
(2)若学校录取总成绩最高的考生,通过计算说明4名考生中哪一名考生会被录取?
23.(本题8分)某校八年级两个班,各选派10名学生参加学校举行的“美丽家乡风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 最高分 平均分 中位数 众数 方差
八(1)班 100 m 93 93 12
八(2)班 99 95 n 93 8.4
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好,请您写出两条支持八(2)班成绩好的理由.
24.(本题8分)某校德育处组织“四品八德”好少年评比活动,每班只有一个名额.现某班有甲、乙、丙三名学生参与竞选,第一轮根据“品行规范”、“学习规范”进行量化考核.甲、乙、丙他们的量化考核成绩(单位:分)分别用两种方式进行了统计,如下表和图1:
(1)请将表和图1中的空缺部分补充完整;
(2)竞选的第二轮是由本班的50位学生进行投票,每票计6分,甲、乙、丙三人的得票情况如图2(没有弃权票,每名学生只能选一人).
①若将“品行规范”、“学习规范”、“得票”三项测试得分按4:3:3的比例确定最后成绩,通过计算谁将会被推选为校“四品八德”好少年.
②若规定得票测试分占20%,要使甲学生最后得分不低于91分,则“品行规范”成绩在总分中所占比例的取值范围应是 .
25.(本题8分)某校八年级(1)班积极响应学校团委的号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐图书400册.特别值得一提的是李保、王刚两位同学在父母的支持下各捐献了90册图书.班长统计了全班捐书情况如下表(被粗心的马小虎用墨水污染了一部分):
册数 4 5 6 7 8 90
人数 6 8 15
2
(1)分别求出该班级捐献7册图书和8册图书的人数;
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪个统计量不能反映该班同学捐书册数的一般状况,说明理由.
26.(本题10分)某厂生产A、B两种产品.其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
A、B产品单价变化统计表
第一次 第二次 第三次
A产品单价(元/件) 6 5.2 6.5
B产品单价(元/件) 3.5 4 3
并求得A产品三次单价的平均数和方差:
:.
(1)补全图中B产品单价变化的折线图.B产品第三次的单价比上一次的单价降低了____%;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小:
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1.求m的值.
参考答案
1.C. 解析:=8.8(环),
故小华这10次射击的平均成绩为8.8环,故选:C.
2.D. 解析:6出现了2次,出现的次数最多,则众数是6;故选:D.
3.C. 解析:∵方差越小数据组中的数据越稳定,而四名同学这10射击的方差中,最小的是S丙2=0.39,∴这四人中丙的成绩最稳定. 故选C.
4.B. 解析:根据题意,有:
小王的最后得分为:;故选:B.
5.A. 解析:根据众数和平均数相等列方程.要分类讨论.
(1)当众数为10时,根据题意得:10+10+x+8=4×10,解得x=12,
则中位数是10;
(2)当x=8时,有两个众数,而平均数为(10×2+8×2)÷4=9,不合题意.
故选A.
6.C. 解析:∵9>8,∴乙、丙两名学生的平均成绩高于甲、丁两名学生,
又∵1<1.2,∴丙的方差小于乙的方差,∴丙发挥稳定,
∴要选一名成绩高且发挥稳定的学生参赛,则应选择的学生是丙.
故选:C.
7.B. 解析:由表可知,样本的平均数为
则估计这4万个数据的平均数约为
故选:B.
8.C. 解析:根据众数、平均数、中位数、方差:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
数据:3,4,5,6,6,6的众数是6,平均数是5,中位数是5.5,方差是,
所以,选项A、B、D正确,选项C错误,故选C.
9.D. 解析:由频数分布图可知,11分的有5人,12分的有10人,13分的有10人,14分的有20人,15分的有5个,所以共有50人,篮球运球成绩在第25位的是13分,在第26位的是14分,所以中位数是(13+14)÷2=13.5,14分的人数最多,所以众数是14,故选D.
10.A. 解析:根据图形可得,小明、小华两名射箭运动员在某次测试中各射箭10次所得的成绩中,小明的成绩与平均成绩离散程度小,而小华的成绩与平均成绩离散程度大,故S1<S2,故选:A.
11.. 解析:这组数据的平均数,故答案为:.
12.5. 解析:中位数的求法:把一组数据按从小到大的顺序排列,最中间的一个数或中间两个数的平均数就是这组数据的平均数. 把手机号码13938891548的11个数字按从小到大的顺序排列为11334588899,则这组数据的中位数为5.
13.. 解析:先计算平均数:(20+10+40+30+90+50)÷6=40,
方差为:S2=[(20-40)2+(10-40)2+(40-40)2+(30-40)2+(90-40)2+(50-40)2]
==,故方差为.
14.15. 解析:根据图示可得,共有:8+10+4+2=24(人),
中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)因此这些足球队员的年龄的中位数是第12名和第13名的平均年龄,为:15.
15.3500. 解析:由10户家庭一周内使用环保方便袋的数量可知,平均每户一周使用的环保方便袋的数量为,
则该小区500户家庭一周内需要环保方便袋约为,
故答案为3500.
16.3. 解析:由题意可知,(3+3+4+x+8)÷5=4,解得x=2,
这组数据从小到大排列2,3,3,4,8,
所以中位数是3.
17.7. 解析:∵组数据m,6,n与1,m,2n,7的平均数都是6,
∴,解得:,若将这两组数据合并为一组数据,按从小到大的顺序排列为1,4,6,7,8,8,8,一共7个数,第四个数是7,则这组数据的中位数是7;故答案为7.
18.20.解析:设这组数据x1,x2,x3的平均数为,
则另一组新数据-2x1+7,-2x2+7,-2x3+7的平均数为-2+7,
∵S2=[(x1-)2+(x2-)2+(x3-)2]=5,
∴方差为S′2= [(-2x1+7+2-7)2+(-2x2+7+2-7)2+(-2x3+7+2-7)2]
= [4(x1-)2+4(x2-)2+4(x3-)2]
=4S2
=4×5
=20,
故答案为:20.
19.解:(1)由题意得:,解得:
答:表中a的值为86
(2)甲候选人的综合成绩为:(分);
乙候选人的综合成绩为:(分);
丁候选人的综合成绩为:(分);
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙
20.解:(1)由题意可得,本次调查的学生数为:30÷30%=100,
阅读时间1.5小时的学生数为:100﹣12﹣30﹣18=40,
补全的条形统计图如图所示,
由补全的条形统计图可知,被调查的学生周末阅读时间众数是1.5小时,中位数是1.5小时,
故答案为1.5,1.5;
(2)所有被调查学生阅读时间的平均数为:×(12×0.5+30×1+40×1.5+18×2)=1.32小时,
即所有被调查同学的平均阅读时间为1.32小时.
(3)估计周末阅读时间不低于1.5小时的人数为500×=290(人).
21.解:(1)乙组的平均分是:(4×1+5×2+6×4+7×4+8×3+9×1)÷15=6.6;
把乙组的数据从小到大排列,最中间的数是第8个数,是7;则中位数是7,
∵成绩达到9分及以上为优秀,
∴甲组的优秀率是×100%=20%;
填表如下:
统计量 平均分 方差 中位数 合格率 优秀率
甲组
20%
乙组 6.6
7
(2)认为甲组的投篮成绩较好,理由如下:
①甲组成绩的合格率比乙组的高;②甲组成绩的优秀率比乙组的高.?
认为乙组的投篮成绩较好,理由如下:
①乙组成绩的中位数比甲组的高;②乙组成绩的方差比甲组的小.
22.解:(1)设专业技能笔试得分占总成绩的百分比是a.
根据题意,得90a+70(1-a)=78.
解这个方程,得a=40%.1-40%=60%.
所以专业技能笔试和课堂教学展示得分占总成绩的百分比分别是40%,60%.
(2)2号考生总成绩为70×0.4+90×0.6=82(分).
3号考生总成绩为86×0.4+80×0.6=82.4(分).
4号考生总成绩为75×0.4+86×0.6=81.6(分).
因为82.4>82>81.6>78,所以3号考生会被录取.
23.解:(1)八(1)班的平均分m=×(88+91+92+93+93+93+94+98+98+100)=94;八(2)班的中位数n==95.5; ∴m=94, n=95.5 .
(2)八(2)班的平均分高于八(1)班;八(2)班的成绩集中在中上游,故支持八(2)班成绩好.
24.解:(1)由统计表可知,乙的学习规范分数85;
(2)解:① 甲得票分,
乙得票分,
丙得票分,
分 ,
分 ,
分 ,
所以乙将被推荐为校“四品八德”好少年;
②设品行规范成绩在总分中所占比例为x,则学习规范在总分中所占比例为(1-0.2- x),根据题意,得,95×x+80×(1-0.2- x)+90×20%≥91,
化简,得15x≥9,解得x≥0.6,1-0.2- x>0,∴x<0.8.
故取值范围:
25.解:(1)设捐7册图书的有x人,捐8册图书的有y人.
则根据题意列出方程:
解得:
捐7册图书的有6人,捐8册图书的有3人.
(2)平均数是10册,中位数是6册,众数是6册.其中平均数10册不能反映该班同学捐书册数的一般情况,因为40名同学中,有38名同学的捐书册数都没有达到10册,平均数主要受到捐书90册的2位同学的捐书册数的影响,故而不能反映该班同学捐书册数的一般情况.
26.解:(1)如图所示
A、B产品单价变化的折线图,如上图.
即:B产品第三次的单价比上一次的单价降低了25%.
(2),
.
∵,∴B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为;
对于B产品,∵m>0,∴第四次单价大于3.
又∵,∴第四次单价小于4.
∴,∴m=25.
