2020-2021学年苏科版七年级下册数学 第七章 平面的图形认识(二)解答题专项培优集训(一)(word版含解析)
文档属性
| 名称 | 2020-2021学年苏科版七年级下册数学 第七章 平面的图形认识(二)解答题专项培优集训(一)(word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 138.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 00:00:00 | ||
图片预览


文档简介
苏科版七年级下册数学
第七章
平面的图形认识(二)
解答题专项培优集训(一)
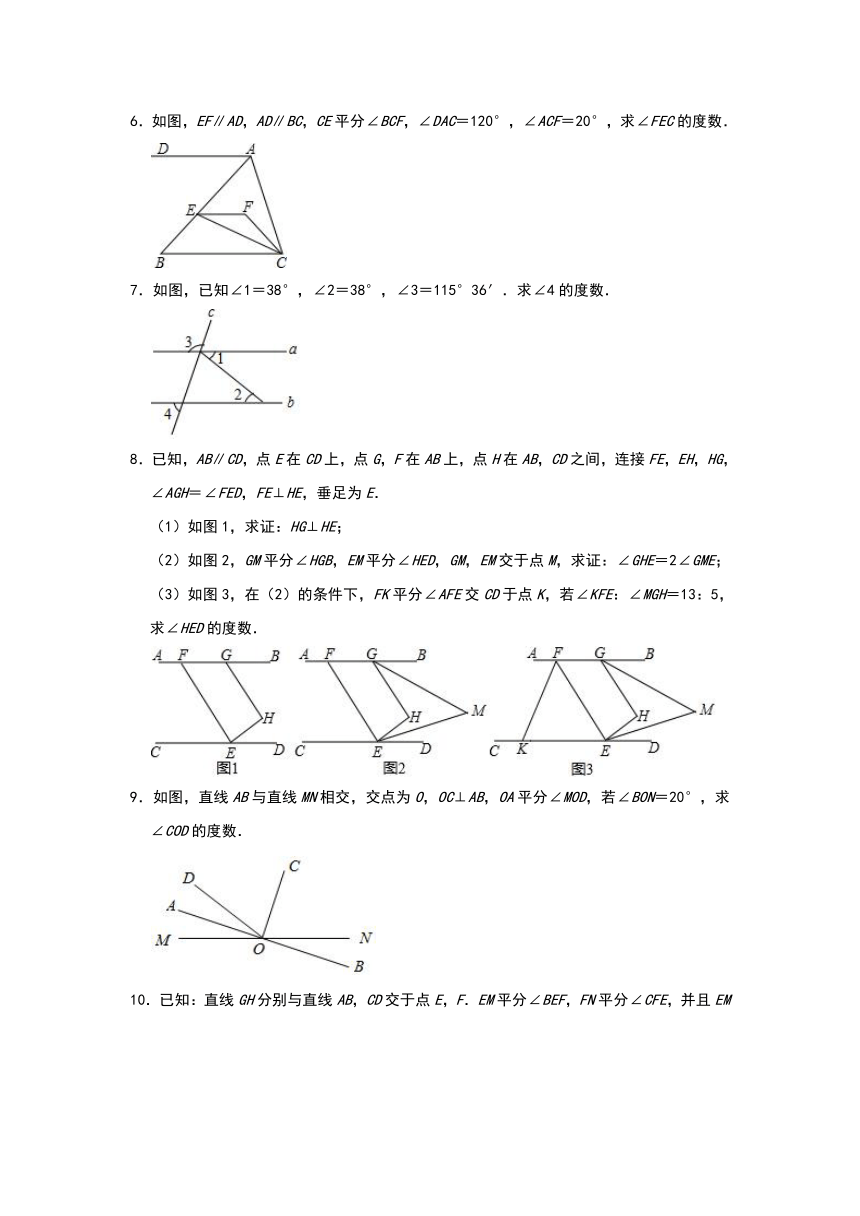
1.如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1.求证:AD平分∠BAC.
下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC于G(已知)
∴∠ADC=∠EGC=90°
∴AD∥EG
(
).
∴∠1=∠2
(
).
=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3
(
).
∴AD平分∠BAC
(
).
2.在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
(1)如图(1),若三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC间的数量关系;
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,∠CFG=β,则∠AEG与∠CFG的数量关系是什么?用含α,β的式子表示(不写理由).
3.如图,已知∠FEA=∠EAF,AE平分∠CAF.
(1)求证:EF∥AC;
(2)若AC平分∠DAB,∠BAF与∠BAD互补,∠FEA﹣∠DAC=50°,求∠F.
4.如图1,已知AB∥CD,∠B=30°,∠D=120°;
(1)若∠E=60°,则∠F=
;
(2)请探索∠E与∠F之间满足的数量关系?说明理由;
(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.
5.如图1,AB∥CD,点E在AB上,点H在CD上,点F在直线AB,CD之间,连接EF,FH,∠AEF+∠CHF=∠EFH.
(1)直接写出∠EFH的度数为
;
(2)如图2,HM平分∠CHF,交FE的延长线于点M,证明:∠FHD﹣2∠FMH=36°;
(3)如图3,点P在FE的延长线上,点K在AB上,点N在∠PEB内,连NE,NK,NK∥FH,∠PEN=2∠NEB,则2∠FHD﹣3∠ENK的值为
.
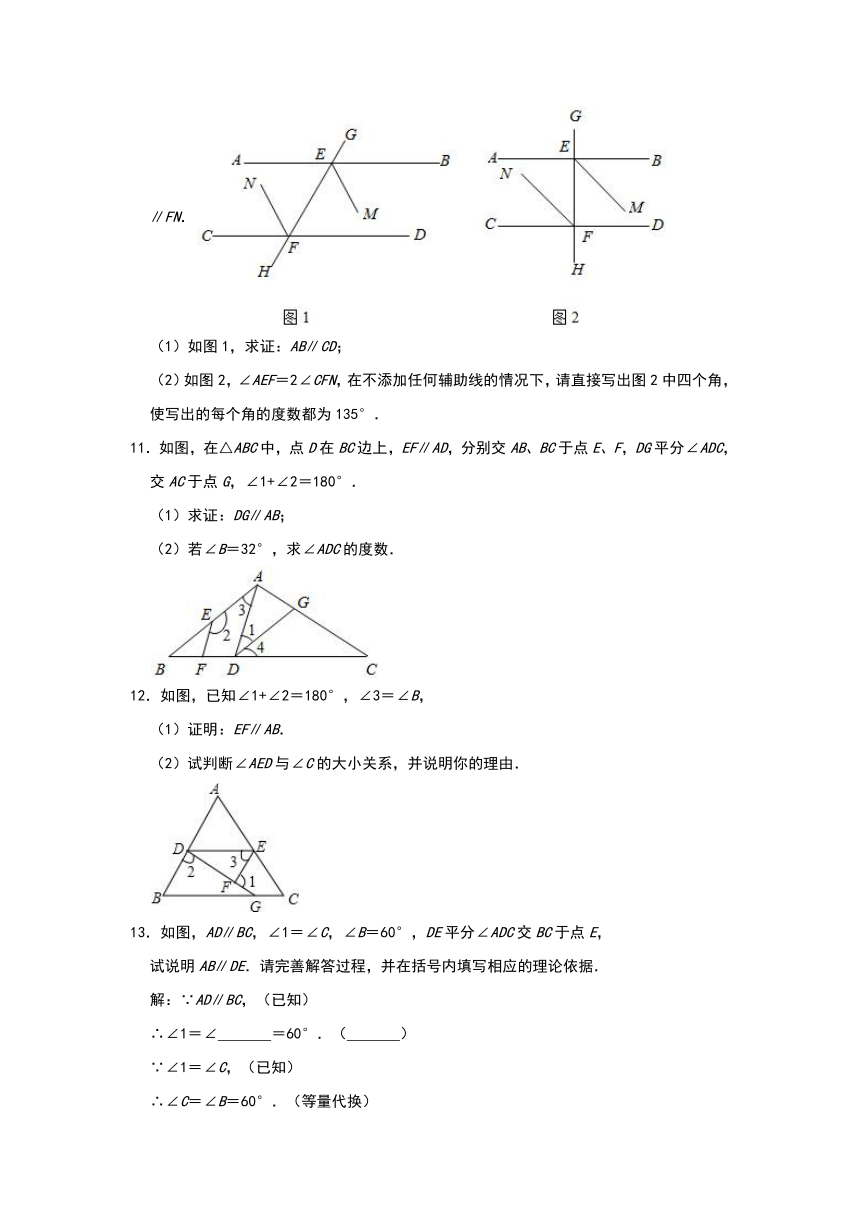
6.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
7.如图,已知∠1=38°,∠2=38°,∠3=115°36′.求∠4的度数.
8.已知,AB∥CD,点E在CD上,点G,F在AB上,点H在AB,CD之间,连接FE,EH,HG,∠AGH=∠FED,FE⊥HE,垂足为E.
(1)如图1,求证:HG⊥HE;
(2)如图2,GM平分∠HGB,EM平分∠HED,GM,EM交于点M,求证:∠GHE=2∠GME;
(3)如图3,在(2)的条件下,FK平分∠AFE交CD于点K,若∠KFE:∠MGH=13:5,求∠HED的度数.
9.如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,求∠COD的度数.
10.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
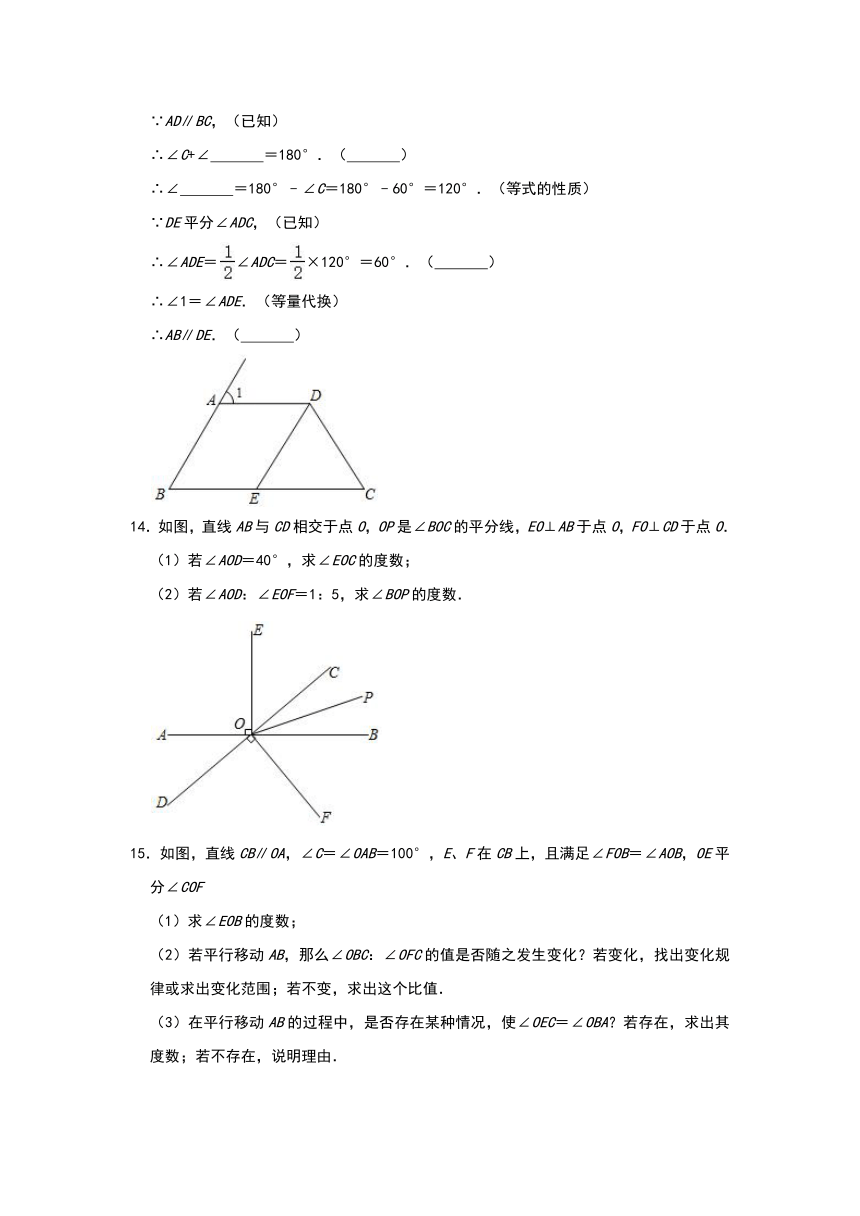
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
11.如图,在△ABC中,点D在BC边上,EF∥AD,分别交AB、BC于点E、F,DG平分∠ADC,交AC于点G,∠1+∠2=180°.
(1)求证:DG∥AB;
(2)若∠B=32°,求∠ADC的度数.
12.如图,已知∠1+∠2=180°,∠3=∠B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.
13.如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,
试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:∵AD∥BC,(已知)
∴∠1=∠
=60°.(
)
∵∠1=∠C,(已知)
∴∠C=∠B=60°.(等量代换)
∵AD∥BC,(已知)
∴∠C+∠
=180°.(
)
∴∠
=180°﹣∠C=180°﹣60°=120°.(等式的性质)
∵DE平分∠ADC,(已知)
∴∠ADE=∠ADC=×120°=60°.(
)
∴∠1=∠ADE.(等量代换)
∴AB∥DE.(
)
14.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,EO⊥AB于点O,FO⊥CD于点O.
(1)若∠AOD=40°,求∠EOC的度数;
(2)若∠AOD:∠EOF=1:5,求∠BOP的度数.
15.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
参考答案
1.解:∵AD⊥BC于D,EG⊥BC于G
(已知)
∴∠ADC=∠EGC=90°
∴AD∥EG,(同位角相等,两直线平行).
∴∠1=∠2,(两直线平行,内错角相等).
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3,(等量代换).
∴AD平分∠BAC.(角平分线的定义)
故答案为:同位角相等,两直线平行;两直线平行,内错角相等;∠E;等量代换;角平分线的定义.
2.解:(1)∵AB∥CD,
∴∠1=∠EGD.
∵∠2+∠FGE+∠EGD=180°,∠2=2∠1,
∴2∠1+60°+∠1=180°,解得∠1=40°;
(2)如图,过点F作FP∥AB,
∵CD∥AB,
∴FP∥AB∥CD.
∴∠AEF=∠EFP,∠FGC=∠GFP.
∴∠AEF+∠FGC=∠EFP+∠GFP=∠EFG.
∵∠EFG=90°,
∴∠AEF+∠FGC=90°;
(3)α+β=300°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°.
即α﹣30°+β﹣90°=180°,
整理得α+β=180°+120°=300°.
3.(1)证明:∵AE平分∠CAF,
∴∠EAF=∠EAC,
∵∠FEA=∠EAF,
∴∠FEA=∠EAC,
∴EF∥AC;
(2)解:∵AC平分∠DAB
∴∠DAC=∠BAC
设∠DAC=∠BAC=x,则∠DAB=2x
∵∠FEA﹣∠DAC=50°
∴∠FEA=∠DAC+50°=x+50°
∴∠EAF=∠EAC=∠FEA=x+50°
∴∠BAF=∠EAF+∠EAC+∠BAC=x+50°+x+50°+x=3x+100°
∵∠BAF与∠BAD互补
∴∠BAF+∠BAD=180°
∴3x+100°+2x=180°
解得:x=16°
∴∠EAF=∠FEA=x+50°=66°
∴∠F=180°﹣∠FEA﹣∠EAF=180°﹣66°﹣66°=48°
4.解:(1)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°
∴∠EFD=∠BEF+30°=90°;
故答案为:90°;
(2)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°,
∴∠EFD=∠BEF+30°;
(3)如图2,过点F作FH∥EP,
由(2)知,∠EFD=∠BEF+30°,
设∠BEF=2x°,则∠EFD=(2x+30)°,
∵EP平分∠BEF,GF平分∠EFD,
∴∠PEF=∠BEF=x°,∠EFG=∠EFD=(x+15)°,
∵FH∥EP,
∴∠PEF=∠EFH=x°,∠P=∠HFG,
∵∠HFG=∠EFG﹣∠EFH=15°,
∴∠P=15°.
5.解:(1)过点F作MN∥AB,如图1所示:
则∠BEF=∠EFM,
∵AB∥CD,
∴MN∥CD,
∴∠DHF=∠HFM,
∴∠AEF+∠CHF+∠EFH=360°,
∵∠AEF+∠CHF=∠EFH,
故∠EFH=108°,
故答案为108°;
(2)过点F作FF′∥AB,过点M作MM′∥AB.
∵AB∥CD,
∴FF′∥MM′∥AB∥CD,
∴∠F′FH=∠FHD,
∴∠3=∠EFH﹣∠F′FH=108°﹣∠FHD,
∴∠M′MF=∠3=108°﹣∠FHD,
∵∠1=∠2,
∴∠1=,
∵MM′∥CD,
∴∠M′MH=∠1,
∴∠FMH+108°﹣∠FHD=,
∴∠FHD﹣2∠FMH=36°;
(3)延长NK交CD于点R,
∵∠AEF+∠CHF=∠EFH,即∠1+∠2=∠3,
而∠1+∠2+∠3=360°,
故∠1+∠2=252°,
设∠NEB=α,则∠PEN=2∠NEB=2α,
则∠1=∠PEB=3α,
而∠2=180°﹣∠4,
故3α﹣∠4=72°,
则2∠FHD﹣3∠ENK=2∠4﹣3(∠NKB﹣∠NEB)=2∠4﹣3(∠4﹣α)=3α﹣∠4=72°,
故答案为72°.
6.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
7.解:∵∠1=∠2,
∴a∥b,
∴∠3=∠5;
又∵∠4+∠5=180°,
∴∠4=180°﹣∠5=180°﹣∠3=180°﹣115°36′=64°24′.
8.证明:(1)∵AB∥CD,
∴∠AFE=∠FED,
∵∠AGH=∠FED,
∴∠AFE=∠AGH,
∴EF∥GH,
∴∠FEH+∠H=180°,
∵FE⊥HE,
∴∠FEH=90°,
∴∠H=180°﹣∠FEH=90°,
∴HG⊥HE;
(2)过点M作MQ∥AB,
∵AB∥CD,
∴MQ∥CD,
过点H作HP∥AB,
∵AB∥CD,
∴HP∥CD,
∵GM平分∠HGB,
∴∠BGM=∠HGM=∠BGH,
∵EM平分∠HED,
∴∠HEM=∠DEM=∠HED,
∵MQ∥AB,
∴∠BGM=∠GMQ,
∵MQ∥CD,
∴∠QME=∠MED,
∴∠GME=∠GMQ+∠QME=∠BGM+∠MED,
∵HP∥AB,
∴∠BGH=∠GHP=2∠BGM,
∵HP∥CD,
∴∠PHE=∠HED=2∠MED,
∴∠GHE=∠GHP+∠PHE=2∠BGM+2∠MED=2(∠BGM+∠MED),
∴∠GHE=∠2GME;
(3)过点M作MQ∥AB,过点H作HP∥AB,
由∠KFE:∠MGH=13:5,设∠KFE=13x,∠MGH=5x,
由(2)可知:∠BGH=2∠MGH=10x,
∵∠AFE+∠BFE=180°,
∴∠AFE=180°﹣10x,
∵FK平分∠AFE,
∴∠AFK=∠KFE=∠AFE,
即,
解得:x=5°,
∴∠BGH=10x=50°,
∵HP∥AB,HP∥CD,
∴∠BGH=∠GHP=50°,∠PHE=∠HED,
∵∠GHE=90°,
∴∠PHE=∠GHE﹣∠GHP=90°﹣50°=40°,
∴∠HED=40°.
9.解:∵∠BON=20°,
∴∠AOM=20°,
∵OA平分∠MOD,
∴∠AOD=∠MOA=20°,
∵OC⊥AB,
∴∠AOC=90°,
∴∠COD=90°﹣20°=70°.
10.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
11.解:(1)证明:∵EF∥AD,
∴∠2+∠3=180°.
∵∠1+∠2=180°.
∴∠1=∠3.
∴DG∥AB;
(2)∵DG平分∠ADC,
∴∠ADC=2∠1=2∠4.
由(1)知DG∥AB,
∴∠4=∠B=32°,
∴∠ADC=2∠4=64°.
12.解:(1)∵∠1+∠DFE=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠DFE,
∴EF∥AB(内错角相等,两直线平行);
(2)∠AED与∠C相等.
∵EF∥AB,
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
13.解:∵AD∥BC,(已知)
∴∠1=∠B=60°.(
两直线平行,同位角相等)
∵∠1=∠C,(已知)
∴∠C=∠B=60°.(等量代换)
∵AD∥BC,(已知)
∴∠C+∠ADC=180°.(两直线平行,同旁内角互补)
∴∠ADC=180°﹣∠C=180°﹣60°=120°.(等式的性质)
∵DE平分∠ADC,(已知)
∴∠ADE=∠ADC=×120°=60°.(角平分线定义)
∴∠1=∠ADE.(等量代换)
∴AB∥DE.(内错角相等,两直线平行.)
故答案为:B,两直线平行,同位角相等,ADC,两直线平行,同旁内角互补,ADC,角平分线定义,内错角相等,两直线平行.
14.解:(1)∵EO⊥AB,
∴∠AOE=90°.
∵∠AOD=40°,
∴∠EOC=180°﹣∠AOD﹣∠AOE
=180°﹣40°﹣90°
=50°.
(2)∵∠AOD:∠EOF=1:5,设∠AOD为x°,则∠EOF为5x°
∵DO⊥FO,
∴∠DOF=90°.
∵∠AOD+∠AOE+∠EOF+∠DOF=360°,
∴x+90°+5x+90°=360°.
解得x=30°,即∠AOD=30°.
又∴∠BOC=∠AOD=30°(对顶角相等),
∵OP是∠BOC的平分线,
∴∠POB=∠BOC=×30°=15°.
15.解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×80°=40°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
第七章
平面的图形认识(二)
解答题专项培优集训(一)
1.如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1.求证:AD平分∠BAC.
下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC于G(已知)
∴∠ADC=∠EGC=90°
∴AD∥EG
(
).
∴∠1=∠2
(
).
=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3
(
).
∴AD平分∠BAC
(
).
2.在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
(1)如图(1),若三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC间的数量关系;
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,∠CFG=β,则∠AEG与∠CFG的数量关系是什么?用含α,β的式子表示(不写理由).
3.如图,已知∠FEA=∠EAF,AE平分∠CAF.
(1)求证:EF∥AC;
(2)若AC平分∠DAB,∠BAF与∠BAD互补,∠FEA﹣∠DAC=50°,求∠F.
4.如图1,已知AB∥CD,∠B=30°,∠D=120°;
(1)若∠E=60°,则∠F=
;
(2)请探索∠E与∠F之间满足的数量关系?说明理由;
(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.
5.如图1,AB∥CD,点E在AB上,点H在CD上,点F在直线AB,CD之间,连接EF,FH,∠AEF+∠CHF=∠EFH.
(1)直接写出∠EFH的度数为
;
(2)如图2,HM平分∠CHF,交FE的延长线于点M,证明:∠FHD﹣2∠FMH=36°;
(3)如图3,点P在FE的延长线上,点K在AB上,点N在∠PEB内,连NE,NK,NK∥FH,∠PEN=2∠NEB,则2∠FHD﹣3∠ENK的值为
.
6.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
7.如图,已知∠1=38°,∠2=38°,∠3=115°36′.求∠4的度数.
8.已知,AB∥CD,点E在CD上,点G,F在AB上,点H在AB,CD之间,连接FE,EH,HG,∠AGH=∠FED,FE⊥HE,垂足为E.
(1)如图1,求证:HG⊥HE;
(2)如图2,GM平分∠HGB,EM平分∠HED,GM,EM交于点M,求证:∠GHE=2∠GME;
(3)如图3,在(2)的条件下,FK平分∠AFE交CD于点K,若∠KFE:∠MGH=13:5,求∠HED的度数.
9.如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,求∠COD的度数.
10.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
11.如图,在△ABC中,点D在BC边上,EF∥AD,分别交AB、BC于点E、F,DG平分∠ADC,交AC于点G,∠1+∠2=180°.
(1)求证:DG∥AB;
(2)若∠B=32°,求∠ADC的度数.
12.如图,已知∠1+∠2=180°,∠3=∠B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.
13.如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,
试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:∵AD∥BC,(已知)
∴∠1=∠
=60°.(
)
∵∠1=∠C,(已知)
∴∠C=∠B=60°.(等量代换)
∵AD∥BC,(已知)
∴∠C+∠
=180°.(
)
∴∠
=180°﹣∠C=180°﹣60°=120°.(等式的性质)
∵DE平分∠ADC,(已知)
∴∠ADE=∠ADC=×120°=60°.(
)
∴∠1=∠ADE.(等量代换)
∴AB∥DE.(
)
14.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,EO⊥AB于点O,FO⊥CD于点O.
(1)若∠AOD=40°,求∠EOC的度数;
(2)若∠AOD:∠EOF=1:5,求∠BOP的度数.
15.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
参考答案
1.解:∵AD⊥BC于D,EG⊥BC于G
(已知)
∴∠ADC=∠EGC=90°
∴AD∥EG,(同位角相等,两直线平行).
∴∠1=∠2,(两直线平行,内错角相等).
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3,(等量代换).
∴AD平分∠BAC.(角平分线的定义)
故答案为:同位角相等,两直线平行;两直线平行,内错角相等;∠E;等量代换;角平分线的定义.
2.解:(1)∵AB∥CD,
∴∠1=∠EGD.
∵∠2+∠FGE+∠EGD=180°,∠2=2∠1,
∴2∠1+60°+∠1=180°,解得∠1=40°;
(2)如图,过点F作FP∥AB,
∵CD∥AB,
∴FP∥AB∥CD.
∴∠AEF=∠EFP,∠FGC=∠GFP.
∴∠AEF+∠FGC=∠EFP+∠GFP=∠EFG.
∵∠EFG=90°,
∴∠AEF+∠FGC=90°;
(3)α+β=300°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°.
即α﹣30°+β﹣90°=180°,
整理得α+β=180°+120°=300°.
3.(1)证明:∵AE平分∠CAF,
∴∠EAF=∠EAC,
∵∠FEA=∠EAF,
∴∠FEA=∠EAC,
∴EF∥AC;
(2)解:∵AC平分∠DAB
∴∠DAC=∠BAC
设∠DAC=∠BAC=x,则∠DAB=2x
∵∠FEA﹣∠DAC=50°
∴∠FEA=∠DAC+50°=x+50°
∴∠EAF=∠EAC=∠FEA=x+50°
∴∠BAF=∠EAF+∠EAC+∠BAC=x+50°+x+50°+x=3x+100°
∵∠BAF与∠BAD互补
∴∠BAF+∠BAD=180°
∴3x+100°+2x=180°
解得:x=16°
∴∠EAF=∠FEA=x+50°=66°
∴∠F=180°﹣∠FEA﹣∠EAF=180°﹣66°﹣66°=48°
4.解:(1)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°
∴∠EFD=∠BEF+30°=90°;
故答案为:90°;
(2)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°,
∴∠EFD=∠BEF+30°;
(3)如图2,过点F作FH∥EP,
由(2)知,∠EFD=∠BEF+30°,
设∠BEF=2x°,则∠EFD=(2x+30)°,
∵EP平分∠BEF,GF平分∠EFD,
∴∠PEF=∠BEF=x°,∠EFG=∠EFD=(x+15)°,
∵FH∥EP,
∴∠PEF=∠EFH=x°,∠P=∠HFG,
∵∠HFG=∠EFG﹣∠EFH=15°,
∴∠P=15°.
5.解:(1)过点F作MN∥AB,如图1所示:
则∠BEF=∠EFM,
∵AB∥CD,
∴MN∥CD,
∴∠DHF=∠HFM,
∴∠AEF+∠CHF+∠EFH=360°,
∵∠AEF+∠CHF=∠EFH,
故∠EFH=108°,
故答案为108°;
(2)过点F作FF′∥AB,过点M作MM′∥AB.
∵AB∥CD,
∴FF′∥MM′∥AB∥CD,
∴∠F′FH=∠FHD,
∴∠3=∠EFH﹣∠F′FH=108°﹣∠FHD,
∴∠M′MF=∠3=108°﹣∠FHD,
∵∠1=∠2,
∴∠1=,
∵MM′∥CD,
∴∠M′MH=∠1,
∴∠FMH+108°﹣∠FHD=,
∴∠FHD﹣2∠FMH=36°;
(3)延长NK交CD于点R,
∵∠AEF+∠CHF=∠EFH,即∠1+∠2=∠3,
而∠1+∠2+∠3=360°,
故∠1+∠2=252°,
设∠NEB=α,则∠PEN=2∠NEB=2α,
则∠1=∠PEB=3α,
而∠2=180°﹣∠4,
故3α﹣∠4=72°,
则2∠FHD﹣3∠ENK=2∠4﹣3(∠NKB﹣∠NEB)=2∠4﹣3(∠4﹣α)=3α﹣∠4=72°,
故答案为72°.
6.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
7.解:∵∠1=∠2,
∴a∥b,
∴∠3=∠5;
又∵∠4+∠5=180°,
∴∠4=180°﹣∠5=180°﹣∠3=180°﹣115°36′=64°24′.
8.证明:(1)∵AB∥CD,
∴∠AFE=∠FED,
∵∠AGH=∠FED,
∴∠AFE=∠AGH,
∴EF∥GH,
∴∠FEH+∠H=180°,
∵FE⊥HE,
∴∠FEH=90°,
∴∠H=180°﹣∠FEH=90°,
∴HG⊥HE;
(2)过点M作MQ∥AB,
∵AB∥CD,
∴MQ∥CD,
过点H作HP∥AB,
∵AB∥CD,
∴HP∥CD,
∵GM平分∠HGB,
∴∠BGM=∠HGM=∠BGH,
∵EM平分∠HED,
∴∠HEM=∠DEM=∠HED,
∵MQ∥AB,
∴∠BGM=∠GMQ,
∵MQ∥CD,
∴∠QME=∠MED,
∴∠GME=∠GMQ+∠QME=∠BGM+∠MED,
∵HP∥AB,
∴∠BGH=∠GHP=2∠BGM,
∵HP∥CD,
∴∠PHE=∠HED=2∠MED,
∴∠GHE=∠GHP+∠PHE=2∠BGM+2∠MED=2(∠BGM+∠MED),
∴∠GHE=∠2GME;
(3)过点M作MQ∥AB,过点H作HP∥AB,
由∠KFE:∠MGH=13:5,设∠KFE=13x,∠MGH=5x,
由(2)可知:∠BGH=2∠MGH=10x,
∵∠AFE+∠BFE=180°,
∴∠AFE=180°﹣10x,
∵FK平分∠AFE,
∴∠AFK=∠KFE=∠AFE,
即,
解得:x=5°,
∴∠BGH=10x=50°,
∵HP∥AB,HP∥CD,
∴∠BGH=∠GHP=50°,∠PHE=∠HED,
∵∠GHE=90°,
∴∠PHE=∠GHE﹣∠GHP=90°﹣50°=40°,
∴∠HED=40°.
9.解:∵∠BON=20°,
∴∠AOM=20°,
∵OA平分∠MOD,
∴∠AOD=∠MOA=20°,
∵OC⊥AB,
∴∠AOC=90°,
∴∠COD=90°﹣20°=70°.
10.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
11.解:(1)证明:∵EF∥AD,
∴∠2+∠3=180°.
∵∠1+∠2=180°.
∴∠1=∠3.
∴DG∥AB;
(2)∵DG平分∠ADC,
∴∠ADC=2∠1=2∠4.
由(1)知DG∥AB,
∴∠4=∠B=32°,
∴∠ADC=2∠4=64°.
12.解:(1)∵∠1+∠DFE=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠DFE,
∴EF∥AB(内错角相等,两直线平行);
(2)∠AED与∠C相等.
∵EF∥AB,
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
13.解:∵AD∥BC,(已知)
∴∠1=∠B=60°.(
两直线平行,同位角相等)
∵∠1=∠C,(已知)
∴∠C=∠B=60°.(等量代换)
∵AD∥BC,(已知)
∴∠C+∠ADC=180°.(两直线平行,同旁内角互补)
∴∠ADC=180°﹣∠C=180°﹣60°=120°.(等式的性质)
∵DE平分∠ADC,(已知)
∴∠ADE=∠ADC=×120°=60°.(角平分线定义)
∴∠1=∠ADE.(等量代换)
∴AB∥DE.(内错角相等,两直线平行.)
故答案为:B,两直线平行,同位角相等,ADC,两直线平行,同旁内角互补,ADC,角平分线定义,内错角相等,两直线平行.
14.解:(1)∵EO⊥AB,
∴∠AOE=90°.
∵∠AOD=40°,
∴∠EOC=180°﹣∠AOD﹣∠AOE
=180°﹣40°﹣90°
=50°.
(2)∵∠AOD:∠EOF=1:5,设∠AOD为x°,则∠EOF为5x°
∵DO⊥FO,
∴∠DOF=90°.
∵∠AOD+∠AOE+∠EOF+∠DOF=360°,
∴x+90°+5x+90°=360°.
解得x=30°,即∠AOD=30°.
又∴∠BOC=∠AOD=30°(对顶角相等),
∵OP是∠BOC的平分线,
∴∠POB=∠BOC=×30°=15°.
15.解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×80°=40°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
