18.1平行四边形同步练习(Word版 含解析)
文档属性
| 名称 | 18.1平行四边形同步练习(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 21:28:45 | ||
图片预览




文档简介
2020-2021学年数学人教版八年级下册18.1平行四边形同步练习
一.选择题(共6小题)
1.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.
其中正确结论的个数为( )
A.1 B.2 C.3 D.4
2.如图,?ABCD中,AC.BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
3.四边形ABCD的对角线AC,BD相交于点O,下列条件:
①AD=BC,AD∥BC;
②AD∥BC,AO=CO;
③AD∥BC,∠ADC=∠ABC;
④AB∥CD,AD=BC中
能判断四边形ABCD是平行四边形的是( )
A.①②④ B.①③④ C.①②③ D.②③④
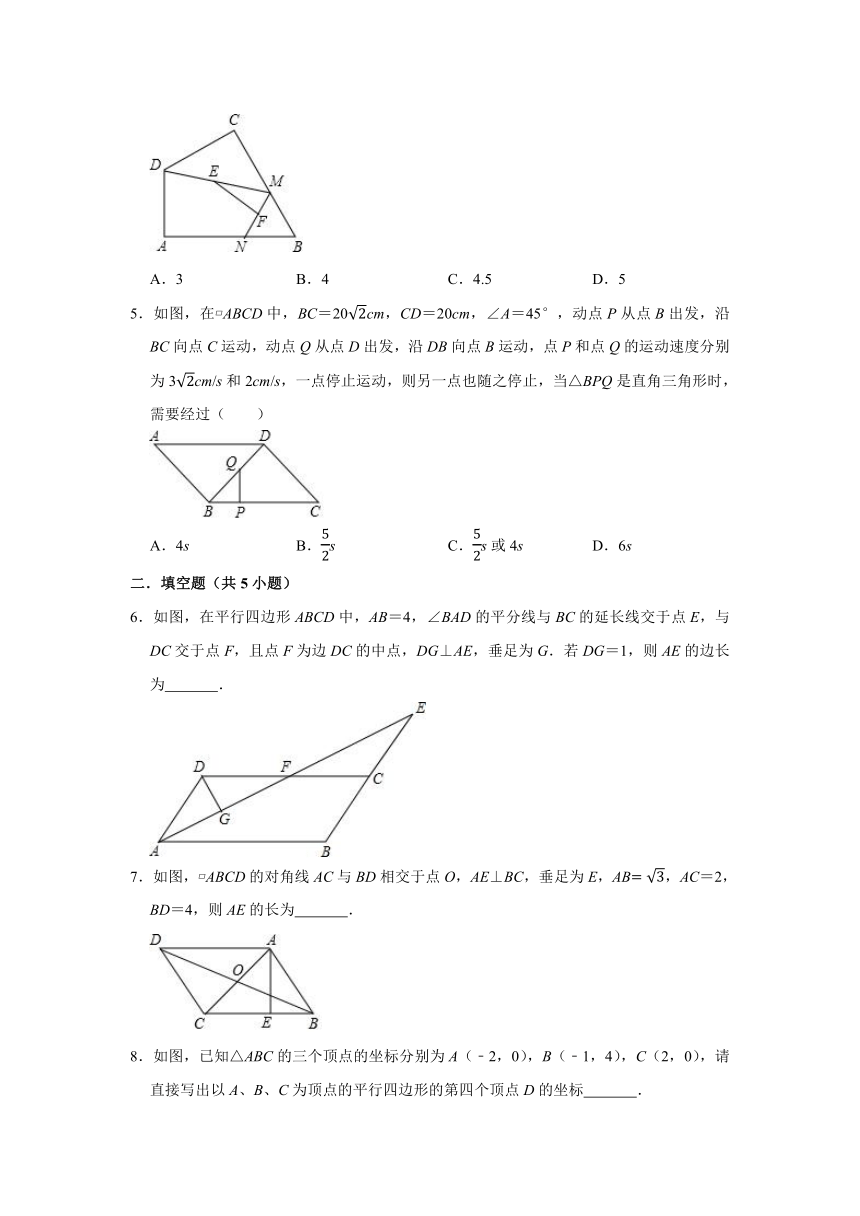
4.如图,四边形ABCD中,∠A=90°,AB=33,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3 B.4 C.4.5 D.5
5.如图,在?ABCD中,BC=202cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为32cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )
A.4s B.52s C.52s或4s D.6s
二.填空题(共5小题)
6.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G.若DG=1,则AE的边长为 .
7.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=3,AC=2,BD=4,则AE的长为 .
8.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,4),C(2,0),请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .
9.如图,△ABC中,BD平分∠ABC,且AD⊥BD,E为AC的中点,AD=6cm,BD=8cm,BC=16cm,则DE的长为 cm.
10.如图,?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为 .
三.解答题(共5小题)
11.如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
12.如图①,四边形ABCD和四边形EBFD都是平行四边形,点E、F在?ABCD的对角线AC上
(1)求证:∠ABE=∠CDF;
(2)若点E、F不在对角线AC上,而在对角线AC所在的直线上,如图②所示,则∠ABE=∠CDF是否还成立?请说明理由.
13.已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
14.如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.
15.已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2
(1)求证:E是AD的中点;
(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2.求证:CD=BF+DF.
一.选择题(共6小题)
1.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.
其中正确结论的个数为( )
A.1 B.2 C.3 D.4
【解答】证明:∵BC=EC,
∴∠CEB=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CEB=∠EBF,
∴∠CBE=∠EBF,
∴①BE平分∠CBF,正确;
∵BC=EC,CF⊥BE,
∴∠ECF=∠BCF,
∴②CF平分∠DCB,正确;
∵DC∥AB,
∴∠DCF=∠CFB,
∵∠ECF=∠BCF,
∴∠CFB=∠BCF,
∴BF=BC,
∴③正确;
∵FB=BC,CF⊥BE,
∴B点一定在FC的垂直平分线上,即PB垂直平分FC,
∴PF=PC,故④正确.
故选:D.
2.如图,?ABCD中,AC.BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
【解答】解:∵?ABCD中,AC.BD为对角线,BC=3,BC边上的高为2,
∴S?ABCD=3×2=6,AD∥BC,
∴OA=OC,∠OAE=∠OCF,
在△AOE和△COF中,
∠OAE=∠OCFOA=OC∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴S△AOE=S△COF,
同理:S△EOG=S△FOH,S△DOG=S△BOH,
∴S阴影=S△ABD=12S?ABCD=12×6=3.
故选:A.
3.四边形ABCD的对角线AC,BD相交于点O,下列条件:
①AD=BC,AD∥BC;
②AD∥BC,AO=CO;
③AD∥BC,∠ADC=∠ABC;
④AB∥CD,AD=BC中
能判断四边形ABCD是平行四边形的是( )
A.①②④ B.①③④ C.①②③ D.②③④
【解答】解:①正确.由一组对边平行且相等的四边形是平行四边形,得出四边形ABCD是平行四边形.
②正确.由AD∥BC,AO=CO,可以证出OB=OD,因为对角线互相平分的四边形是平行四边形,所以四边形ABCD是平行四边形.
③正确.由AD∥BC,∠ADC=∠ABC,可以推出∠BAD=∠BCD,因为两组对角分别相等的四边形是平行四边形,所以四边形ABCD是平行四边形.
④错误.四边形ABCD可能是等腰梯形.
故选:C.
4.如图,四边形ABCD中,∠A=90°,AB=33,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3 B.4 C.4.5 D.5
【解答】解:如图,连接DN,
∵DE=EM,FN=FM,
∴EF=12DN,
当点N与点B重合时,DN的值最大即EF最大,
在Rt△ABD中,∵∠A=90°,AD=3,AB=33,
∴BD=AD2+AB2=32+(33)2=6,
∴EF的最大值=12BD=3.
故选:A.
5.如图,在?ABCD中,BC=202cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为32cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )
A.4s B.52s C.52s或4s D.6s
【解答】解:如图作DH⊥BC于H.
∵四边形ABCD是平行四边形,
∴∠C=∠A=45°,
∴DH=CH,
∵CD=20,
∴DH=CH=102,
在Rt△DBH中,BD=DH2+BH2=20,
∴BD=CD,
∴∠DBC=∠C=45°,
∴当BQ=2PB或PB=2BQ时,△BQP是直角三角形,
∴20﹣2t=2×32t或32t=2(20﹣2t),
解得t=52或4s,
故选:C.
二.填空题(共5小题)
6.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G.若DG=1,则AE的边长为 43 .
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=4,
∴∠AFD=∠BAF,
∵点F为边DC的中点,
∴DF=12CD=2,
∵AE平分∠BAD,
∴∠DAF=∠BAF,
∴∠DAF=∠AFD,
∴AD=DF=2,
∵DG⊥AE,
∴AG=FG=DF2-DG2=22-12=3,
∴AF=23,
∵AD∥BC,
∴△ADF∽△ECF,
∴AF:EF=DF:CF=1,
∴EF=AF=23,
∴AE=43.
故答案为:43.
7.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=3,AC=2,BD=4,则AE的长为 2217 .
【解答】解:∵AC=2,BD=4,四边形ABCD是平行四边形,
∴AO=12AC=1,BO=12BD=2,
∵AB=3,
∴AB2+AO2=BO2,
∴∠BAC=90°,
∵在Rt△BAC中,BC=AB2+AC2=(3)2+22=7,
S△BAC=12×AB×AC=12×BC×AE,
∴23=7AE,
∴AE=2217,
故答案为:2217.
8.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,4),C(2,0),请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标 (3,4),(﹣5,4),(1,﹣4) .
【解答】解:AC=2﹣(﹣2)=4,
当平行四边形是BACD时,把B向右平移4个单位长度,则D的坐标是(3,4);
当平行四边形是ACBD时,把B向左平移4个单位长度就是D,则D的坐标是(﹣5,4);
当平行四边形是BADC时,AC的中点的坐标是原点O(0,0).
把B向右平移1个单位长度,向下平移4个单位长度得到AC中点O,则把A向右平移2个单位长度,向下平移8个单位长度即可得到D,D的坐标是(1,﹣4).
故答案是:(3,4),(﹣5,4),(1,﹣4).
9.如图,△ABC中,BD平分∠ABC,且AD⊥BD,E为AC的中点,AD=6cm,BD=8cm,BC=16cm,则DE的长为 3 cm.
【解答】解:如图,延长AD交BC于F,
∵BD平分∠ABC,
∴∠ABD=∠FBD,
∵AD⊥BD,
∴∠BDA=∠BDF=90°,AB=AD2+BD2=62+82=10(cm),
在△BDF和△BDA中,∠FBD=∠ABDBD=BD∠BDA=∠BDF,
∴△BDF≌△BDA(ASA),
∴DF=AD,FB=AB=10cm,
∴CF=BC﹣FB=16﹣10=6cm,
又∵点E为AC的中点,
∴DE是△ACF的中位线,
∴DE=12CF=3cm.
故答案为:3.
10.如图,?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为 2 .
【解答】解法一:∵四边形ABCD是平行四边形,BD=2,
∴BE=12BD=1.
如图2,连接BB′.
根据折叠的性质知,∠AEB=∠AEB′=45°,
BE=B′E.
∴∠BEB′=90°,
∴△BB′E是等腰直角三角形,
则BB′=2BE=2.
又∵BE=DE,B′E⊥BD,
∴DB′=BB′=2.
解法二:如图2,
根据折叠的性质知,∠BEA=∠B′EA=45°,则∠B′ED=90°.
又由折叠的性质和平行四边形ABCD的性质知,BE=B′E=DE,
∴△B′ED是等腰直角三角形,
∴DB′=2DE=2×12BD=2
故答案为:2.
三.解答题(共5小题)
11.如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,∠D=∠ECFDE=CE∠AED=∠FEC,
∴△ADE≌△FCE(ASA);
(2)解:∵△ADE≌△FCE,
∴AD=FC,
∵AD=BC,AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°﹣2×36°=108°.
12.如图①,四边形ABCD和四边形EBFD都是平行四边形,点E、F在?ABCD的对角线AC上
(1)求证:∠ABE=∠CDF;
(2)若点E、F不在对角线AC上,而在对角线AC所在的直线上,如图②所示,则∠ABE=∠CDF是否还成立?请说明理由.
【解答】(1)证明:连接BD交AC于O,如图①所示:
∵四边形ABCD和四边形EBFD都是平行四边形,
∴AB∥CD,AB=CD,OA=OC,OE=OF,
∴∠BAE=∠DCF,AE=CF,
在△ABE和△CDF中,AB=CD∠BAE=∠DCFAE=CF,
∴ABE≌△CDF(SAS),
∴∠ABE=∠CDF;
(2)解:∠ABE=∠CDF还成立,理由如下:
连接BD交AC于O,如图②所示:
∵四边形ABCD和四边形EBFD都是平行四边形,
∴BE∥DF,BE=DF,OA=OC,OE=OF,
∴∠BEA=∠DFC,AE=CF,
在△ABE和△CDF中,BE=DF∠BEA=∠DFCAE=CF,
∴ABE≌△CDF(SAS),
∴∠ABE=∠CDF.
13.已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
【解答】证明:(1)∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD﹣∠BAD,∠DAC=∠BAC﹣∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
AF=AD∠BAF=∠CADAB=AC,
∴△AFB≌△ADC(SAS);
(2)由①得△AFB≌△ADC,
∴∠ABF=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABF=∠BAC,
∴FB∥AC,
又∵BC∥EF,
∴四边形BCEF是平行四边形;
(3)成立,理由如下:
∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠BAC﹣∠FAE,∠DAC=∠FAD﹣∠FAE,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
AF=AD∠BAF=∠CADAB=AC,
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
14.如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.
【解答】解:问题一,取AC中点P,连接PF,PE,
可知PE=AB2,
PE∥AB,
∴∠PEF=∠ANF,
同理PF=CD2,
PF∥CD,
∴∠PFE=∠CME,
又∵PE=PF,
∴∠PFE=∠PEF,
∴∠OMN=∠ONM,
∴△OMN为等腰三角形.
问题二,结论:△AGD是直角三角形.
证明:如图连接BD,取BD的中点H,连接HF、HE,
∵F是AD的中点,
∴HF∥AB,HF=12AB,
同理,HE∥CD,HE=12CD,
∵AB=CD
∴HF=HE,
∵∠EFC=60°,
∴∠HEF=60°,
∴∠HEF=∠HFE=60°,
∴△EHF是等边三角形,
∴∠3=∠EFC=∠AFG=60°,
∴△AGF是等边三角形.
∵AF=FD,
∴GF=FD,
∴∠FGD=∠FDG=30°
∴∠AGD=90°
即△AGD是直角三角形.
15.已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2
(1)求证:E是AD的中点;
(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2.求证:CD=BF+DF.
【解答】解:∵四边形ABCD为平行四边形,
∴AD=BC,AB=CD,∠A=∠C,
在△AEB和△CDG中,
∠A=∠CAB=CD∠1=∠2,
∴△AEB≌△CDG,
∴AE=CG,
∵G为BC中点,
∴CG=12BC,
∴AE=12BC,
∵AD=BC,
∴AE=12AD,
∴E是AD的中点;
(2)如图,延长DF,BE,相交于点H,
∵E为AD的中点,G为BC的中点,
∴DE=12AD,BG=12BC,
:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∴DE=BG,DE∥BG,
∴四边形EBGD为平行四边形,
∴BE∥DG,
∴∠H=∠2,
∵∠3=∠2,
∴∠H=∠3,
∴BF=HF,
∵∠1=∠2,
∴∠H=∠1,
∵E为AD的中点,
∴AE=DE,
在△AEB和△DEH中,
∠1=∠H∠AEB=∠DEGAE=DE,
∴△AEB≌△DEH,
∴AB=DH,
∵AB=CD,
∴CD=DH,
∵DH=HF+FD,HF=BF,
∴DH=BF+FD,
∴CD=BF+FD。
一.选择题(共6小题)
1.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.
其中正确结论的个数为( )
A.1 B.2 C.3 D.4
2.如图,?ABCD中,AC.BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
3.四边形ABCD的对角线AC,BD相交于点O,下列条件:
①AD=BC,AD∥BC;
②AD∥BC,AO=CO;
③AD∥BC,∠ADC=∠ABC;
④AB∥CD,AD=BC中
能判断四边形ABCD是平行四边形的是( )
A.①②④ B.①③④ C.①②③ D.②③④
4.如图,四边形ABCD中,∠A=90°,AB=33,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3 B.4 C.4.5 D.5
5.如图,在?ABCD中,BC=202cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为32cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )
A.4s B.52s C.52s或4s D.6s
二.填空题(共5小题)
6.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G.若DG=1,则AE的边长为 .
7.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=3,AC=2,BD=4,则AE的长为 .
8.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,4),C(2,0),请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .
9.如图,△ABC中,BD平分∠ABC,且AD⊥BD,E为AC的中点,AD=6cm,BD=8cm,BC=16cm,则DE的长为 cm.
10.如图,?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为 .
三.解答题(共5小题)
11.如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
12.如图①,四边形ABCD和四边形EBFD都是平行四边形,点E、F在?ABCD的对角线AC上
(1)求证:∠ABE=∠CDF;
(2)若点E、F不在对角线AC上,而在对角线AC所在的直线上,如图②所示,则∠ABE=∠CDF是否还成立?请说明理由.
13.已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
14.如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.
15.已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2
(1)求证:E是AD的中点;
(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2.求证:CD=BF+DF.
一.选择题(共6小题)
1.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.
其中正确结论的个数为( )
A.1 B.2 C.3 D.4
【解答】证明:∵BC=EC,
∴∠CEB=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CEB=∠EBF,
∴∠CBE=∠EBF,
∴①BE平分∠CBF,正确;
∵BC=EC,CF⊥BE,
∴∠ECF=∠BCF,
∴②CF平分∠DCB,正确;
∵DC∥AB,
∴∠DCF=∠CFB,
∵∠ECF=∠BCF,
∴∠CFB=∠BCF,
∴BF=BC,
∴③正确;
∵FB=BC,CF⊥BE,
∴B点一定在FC的垂直平分线上,即PB垂直平分FC,
∴PF=PC,故④正确.
故选:D.
2.如图,?ABCD中,AC.BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
【解答】解:∵?ABCD中,AC.BD为对角线,BC=3,BC边上的高为2,
∴S?ABCD=3×2=6,AD∥BC,
∴OA=OC,∠OAE=∠OCF,
在△AOE和△COF中,
∠OAE=∠OCFOA=OC∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴S△AOE=S△COF,
同理:S△EOG=S△FOH,S△DOG=S△BOH,
∴S阴影=S△ABD=12S?ABCD=12×6=3.
故选:A.
3.四边形ABCD的对角线AC,BD相交于点O,下列条件:
①AD=BC,AD∥BC;
②AD∥BC,AO=CO;
③AD∥BC,∠ADC=∠ABC;
④AB∥CD,AD=BC中
能判断四边形ABCD是平行四边形的是( )
A.①②④ B.①③④ C.①②③ D.②③④
【解答】解:①正确.由一组对边平行且相等的四边形是平行四边形,得出四边形ABCD是平行四边形.
②正确.由AD∥BC,AO=CO,可以证出OB=OD,因为对角线互相平分的四边形是平行四边形,所以四边形ABCD是平行四边形.
③正确.由AD∥BC,∠ADC=∠ABC,可以推出∠BAD=∠BCD,因为两组对角分别相等的四边形是平行四边形,所以四边形ABCD是平行四边形.
④错误.四边形ABCD可能是等腰梯形.
故选:C.
4.如图,四边形ABCD中,∠A=90°,AB=33,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3 B.4 C.4.5 D.5
【解答】解:如图,连接DN,
∵DE=EM,FN=FM,
∴EF=12DN,
当点N与点B重合时,DN的值最大即EF最大,
在Rt△ABD中,∵∠A=90°,AD=3,AB=33,
∴BD=AD2+AB2=32+(33)2=6,
∴EF的最大值=12BD=3.
故选:A.
5.如图,在?ABCD中,BC=202cm,CD=20cm,∠A=45°,动点P从点B出发,沿BC向点C运动,动点Q从点D出发,沿DB向点B运动,点P和点Q的运动速度分别为32cm/s和2cm/s,一点停止运动,则另一点也随之停止,当△BPQ是直角三角形时,需要经过( )
A.4s B.52s C.52s或4s D.6s
【解答】解:如图作DH⊥BC于H.
∵四边形ABCD是平行四边形,
∴∠C=∠A=45°,
∴DH=CH,
∵CD=20,
∴DH=CH=102,
在Rt△DBH中,BD=DH2+BH2=20,
∴BD=CD,
∴∠DBC=∠C=45°,
∴当BQ=2PB或PB=2BQ时,△BQP是直角三角形,
∴20﹣2t=2×32t或32t=2(20﹣2t),
解得t=52或4s,
故选:C.
二.填空题(共5小题)
6.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G.若DG=1,则AE的边长为 43 .
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=4,
∴∠AFD=∠BAF,
∵点F为边DC的中点,
∴DF=12CD=2,
∵AE平分∠BAD,
∴∠DAF=∠BAF,
∴∠DAF=∠AFD,
∴AD=DF=2,
∵DG⊥AE,
∴AG=FG=DF2-DG2=22-12=3,
∴AF=23,
∵AD∥BC,
∴△ADF∽△ECF,
∴AF:EF=DF:CF=1,
∴EF=AF=23,
∴AE=43.
故答案为:43.
7.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=3,AC=2,BD=4,则AE的长为 2217 .
【解答】解:∵AC=2,BD=4,四边形ABCD是平行四边形,
∴AO=12AC=1,BO=12BD=2,
∵AB=3,
∴AB2+AO2=BO2,
∴∠BAC=90°,
∵在Rt△BAC中,BC=AB2+AC2=(3)2+22=7,
S△BAC=12×AB×AC=12×BC×AE,
∴23=7AE,
∴AE=2217,
故答案为:2217.
8.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,4),C(2,0),请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标 (3,4),(﹣5,4),(1,﹣4) .
【解答】解:AC=2﹣(﹣2)=4,
当平行四边形是BACD时,把B向右平移4个单位长度,则D的坐标是(3,4);
当平行四边形是ACBD时,把B向左平移4个单位长度就是D,则D的坐标是(﹣5,4);
当平行四边形是BADC时,AC的中点的坐标是原点O(0,0).
把B向右平移1个单位长度,向下平移4个单位长度得到AC中点O,则把A向右平移2个单位长度,向下平移8个单位长度即可得到D,D的坐标是(1,﹣4).
故答案是:(3,4),(﹣5,4),(1,﹣4).
9.如图,△ABC中,BD平分∠ABC,且AD⊥BD,E为AC的中点,AD=6cm,BD=8cm,BC=16cm,则DE的长为 3 cm.
【解答】解:如图,延长AD交BC于F,
∵BD平分∠ABC,
∴∠ABD=∠FBD,
∵AD⊥BD,
∴∠BDA=∠BDF=90°,AB=AD2+BD2=62+82=10(cm),
在△BDF和△BDA中,∠FBD=∠ABDBD=BD∠BDA=∠BDF,
∴△BDF≌△BDA(ASA),
∴DF=AD,FB=AB=10cm,
∴CF=BC﹣FB=16﹣10=6cm,
又∵点E为AC的中点,
∴DE是△ACF的中位线,
∴DE=12CF=3cm.
故答案为:3.
10.如图,?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为 2 .
【解答】解法一:∵四边形ABCD是平行四边形,BD=2,
∴BE=12BD=1.
如图2,连接BB′.
根据折叠的性质知,∠AEB=∠AEB′=45°,
BE=B′E.
∴∠BEB′=90°,
∴△BB′E是等腰直角三角形,
则BB′=2BE=2.
又∵BE=DE,B′E⊥BD,
∴DB′=BB′=2.
解法二:如图2,
根据折叠的性质知,∠BEA=∠B′EA=45°,则∠B′ED=90°.
又由折叠的性质和平行四边形ABCD的性质知,BE=B′E=DE,
∴△B′ED是等腰直角三角形,
∴DB′=2DE=2×12BD=2
故答案为:2.
三.解答题(共5小题)
11.如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,∠D=∠ECFDE=CE∠AED=∠FEC,
∴△ADE≌△FCE(ASA);
(2)解:∵△ADE≌△FCE,
∴AD=FC,
∵AD=BC,AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°﹣2×36°=108°.
12.如图①,四边形ABCD和四边形EBFD都是平行四边形,点E、F在?ABCD的对角线AC上
(1)求证:∠ABE=∠CDF;
(2)若点E、F不在对角线AC上,而在对角线AC所在的直线上,如图②所示,则∠ABE=∠CDF是否还成立?请说明理由.
【解答】(1)证明:连接BD交AC于O,如图①所示:
∵四边形ABCD和四边形EBFD都是平行四边形,
∴AB∥CD,AB=CD,OA=OC,OE=OF,
∴∠BAE=∠DCF,AE=CF,
在△ABE和△CDF中,AB=CD∠BAE=∠DCFAE=CF,
∴ABE≌△CDF(SAS),
∴∠ABE=∠CDF;
(2)解:∠ABE=∠CDF还成立,理由如下:
连接BD交AC于O,如图②所示:
∵四边形ABCD和四边形EBFD都是平行四边形,
∴BE∥DF,BE=DF,OA=OC,OE=OF,
∴∠BEA=∠DFC,AE=CF,
在△ABE和△CDF中,BE=DF∠BEA=∠DFCAE=CF,
∴ABE≌△CDF(SAS),
∴∠ABE=∠CDF.
13.已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
【解答】证明:(1)∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD﹣∠BAD,∠DAC=∠BAC﹣∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
AF=AD∠BAF=∠CADAB=AC,
∴△AFB≌△ADC(SAS);
(2)由①得△AFB≌△ADC,
∴∠ABF=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABF=∠BAC,
∴FB∥AC,
又∵BC∥EF,
∴四边形BCEF是平行四边形;
(3)成立,理由如下:
∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠BAC﹣∠FAE,∠DAC=∠FAD﹣∠FAE,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
AF=AD∠BAF=∠CADAB=AC,
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
14.如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.
【解答】解:问题一,取AC中点P,连接PF,PE,
可知PE=AB2,
PE∥AB,
∴∠PEF=∠ANF,
同理PF=CD2,
PF∥CD,
∴∠PFE=∠CME,
又∵PE=PF,
∴∠PFE=∠PEF,
∴∠OMN=∠ONM,
∴△OMN为等腰三角形.
问题二,结论:△AGD是直角三角形.
证明:如图连接BD,取BD的中点H,连接HF、HE,
∵F是AD的中点,
∴HF∥AB,HF=12AB,
同理,HE∥CD,HE=12CD,
∵AB=CD
∴HF=HE,
∵∠EFC=60°,
∴∠HEF=60°,
∴∠HEF=∠HFE=60°,
∴△EHF是等边三角形,
∴∠3=∠EFC=∠AFG=60°,
∴△AGF是等边三角形.
∵AF=FD,
∴GF=FD,
∴∠FGD=∠FDG=30°
∴∠AGD=90°
即△AGD是直角三角形.
15.已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2
(1)求证:E是AD的中点;
(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2.求证:CD=BF+DF.
【解答】解:∵四边形ABCD为平行四边形,
∴AD=BC,AB=CD,∠A=∠C,
在△AEB和△CDG中,
∠A=∠CAB=CD∠1=∠2,
∴△AEB≌△CDG,
∴AE=CG,
∵G为BC中点,
∴CG=12BC,
∴AE=12BC,
∵AD=BC,
∴AE=12AD,
∴E是AD的中点;
(2)如图,延长DF,BE,相交于点H,
∵E为AD的中点,G为BC的中点,
∴DE=12AD,BG=12BC,
:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∴DE=BG,DE∥BG,
∴四边形EBGD为平行四边形,
∴BE∥DG,
∴∠H=∠2,
∵∠3=∠2,
∴∠H=∠3,
∴BF=HF,
∵∠1=∠2,
∴∠H=∠1,
∵E为AD的中点,
∴AE=DE,
在△AEB和△DEH中,
∠1=∠H∠AEB=∠DEGAE=DE,
∴△AEB≌△DEH,
∴AB=DH,
∵AB=CD,
∴CD=DH,
∵DH=HF+FD,HF=BF,
∴DH=BF+FD,
∴CD=BF+FD。
