第12章 第3节机械效率—2020-2021学年人教版八年级物理下册课件(29张PPT)
文档属性
| 名称 | 第12章 第3节机械效率—2020-2021学年人教版八年级物理下册课件(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-25 14:19:41 | ||
图片预览





文档简介
机械效率
12.3
课前回顾
1、什么是功?
2、功的计算式是什么?
3、你如何理解功的原理?
教学目标
1、了解什么是“有用功”、“额外
功”和“总功”。
2、理解什么是“机械效率”。
1、“效率”这个词大家并不陌生,谁能给大家解释一下?
2、机械帮助我们做功也会涉及效率问题,我们称为机械效率,要研究机械效率就要先研究使用机械效率做功的情况
情景导入
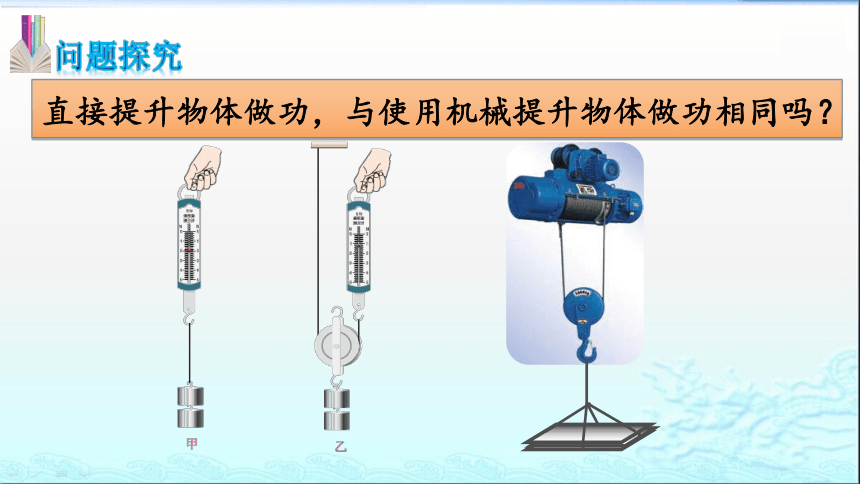
直接提升物体做功,与使用机械提升物体做功相同吗?
问题探究
G/N
h/m
W直/J
F/N
s/m
W机/J
2
0.1
0.2
1.2
0.2
0.24
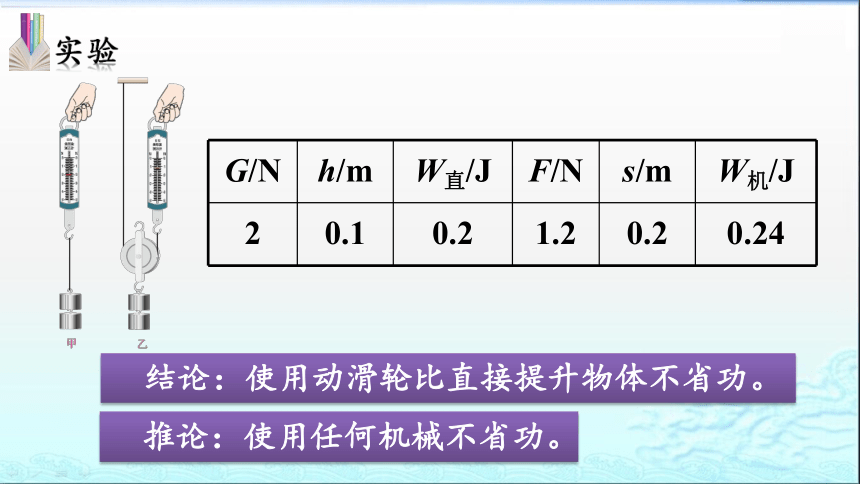
结论:使用动滑轮比直接提升物体不省功。
推论:使用任何机械不省功。
实验
G/N
h/m
W直/J
F/N
s/m
W机/J
2
0.1
0.2
1.2
0.2
0.24
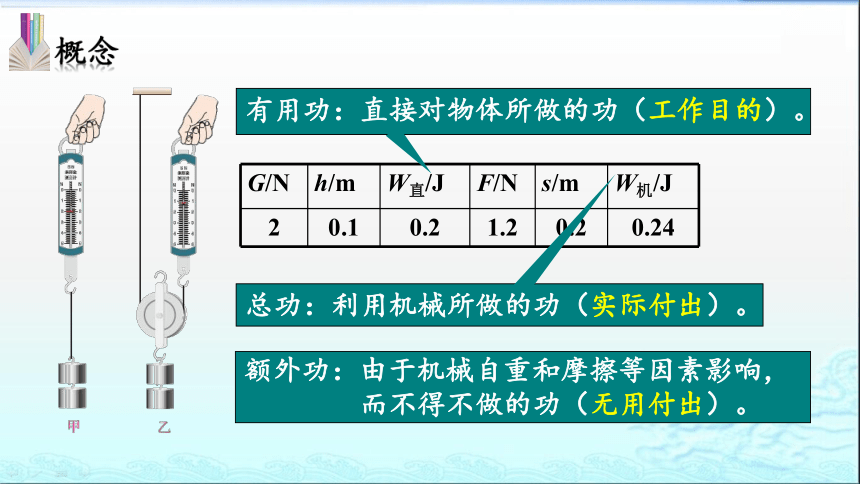
额外功:由于机械自重和摩擦等因素影响,
而不得不做的功(无用付出)。
有用功:直接对物体所做的功(工作目的)。
总功:利用机械所做的功(实际付出)。
概念
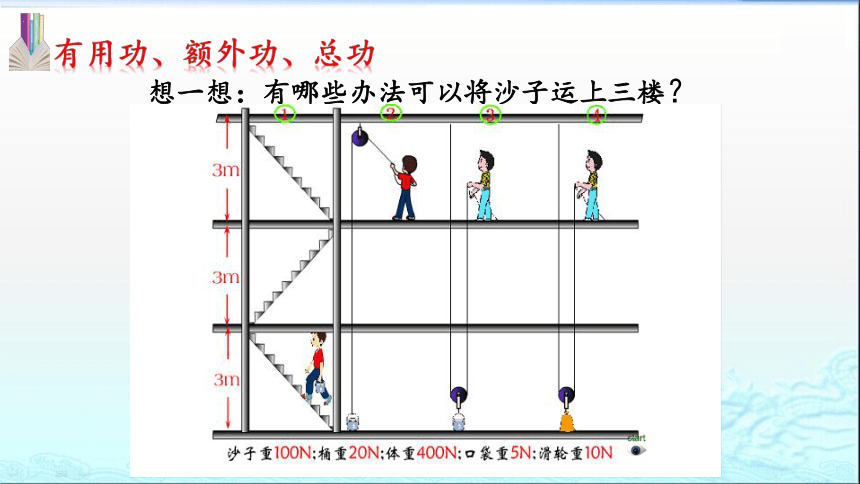
想一想:有哪些办法可以将沙子运上三楼?
有用功、额外功、总功
①
3克服自重做功
1对砂子做功
2对桶做功
②
1对砂子做功
2对桶做功
③
1对砂子做功
2对桶做功
3对动滑轮做功
④
1对砂子做功
2对口袋做功
3对动滑轮做功
思考:提升物体的过程中动力(人)对哪些物体做了功?
有用功概念:
满足我们做功的目的,对我们有价值的功,
计作:W有用
对重物(沙子)做的功
①
3克服自重做功
1对砂子做功
2对桶做功
②
1对砂子做功
2对桶做功
③
1对砂子做功
2对桶做功
3对动滑轮做功
④
1对砂子做功
2对口袋做功
3对动滑轮做功
问题1:哪些功达到了我们做功的目的?
1.桶、动滑轮、口袋等也随重物一起上升,也提升了它们,克服这些重力做的功。
2.此外,机械运转时都有摩擦克服机械的摩擦做的功。
额外功概念:
对我们既无利用价值而又不得不做的功。
计作:W额外
问题2:哪些功对我们没有价值,但又不得不做的功?
①
3克服自重做功
1对砂子做功
2对桶做功
②
1对砂子做功
2对桶做功
③
1对砂子做功
2对桶做功
3对动滑轮做功
④
1对砂子做功
2对口袋做功
3对动滑轮做功
三种功的计算
1、有用功(W有):对人们有用的功。
计算:提升物体(克服物重做功):W有=Gh
水平匀速(克服摩擦做功):W有=fS
2 、额外功(W额):人们不需要但又不得不做的功。
计算:提升物体(只计动滑轮重):W额=G动h
斜 面(克服摩擦做的功):W额=fL
3 、总功(W总):有用功与额外功的总和
(运用机械时动力F所做的功)。
计算:滑轮组:W总=FS [ F=(G+G动)/n;S=nh ];
斜 面:W总 =FL
4 、三者关系: W总= W有+ W额
1、用水桶从井中提水时,
所做的有用功是 ,
额外功是 ,
总功是 ;
2、如果桶掉到井里,从井里捞桶时,捞上来的桶里带了一些水,有用功是 ,
额外功是 ,
总功是 。
克服水的重力做功
克服桶的重力做功
拉力所做的功
克服桶的重力做功
克服水的重力做功
拉力所做的功
点拨释疑
算一算:算出有用功,额外功 总功分别是多少?
砂子重100N;桶重20N;人重400N;地面到三楼高6m
总功
=3120J
算一算:算出有用功,额外功 总功分别是多少?
1、对砂子做功(有用功)
W砂=G砂h=100N×6m=600J
2、对桶做功(额外功)
W桶=G桶h=20N×6m=120J
3、克服自重做功(额外功)
W人=G人h=400N×6m=2400J
砂子重100N;桶重20N;地面到三楼高6m
算一算:算出有用功,额外功 总功分别是多少?
总功
=720J
1、对砂子做功(有用功)
W砂=G砂h=100N×6m=600J
2、对桶做功(额外功)
W桶=G桶h=20N×6m=120J
砂子重100N;桶重20N;动滑轮重10N;地面到三楼高6m
算一算:算出有用功,额外功 总功分别是多少?
总功
=780J
1、对砂子做功(有用功)
W砂=G砂h=100N×6m=600J
2、对桶做功(额外功)
W桶=G桶h=20N×6m=120J
3、对滑轮做功(额外功)
W人=G滑h=10N×6m=60J
砂子重100N;动滑轮重10N;口袋重5N;地面到三楼高6m
算一算:算出有用功,额外功 总功分别是多少?
总功
=690J
1、对砂子做功(有用功)
W砂=G砂h=100N×6m=600J
2、对口袋做功(额外功)
W桶=G袋h=5N×6m=30J
3、对动滑轮做功(额外功)
W人=G滑h=10N×6m=60J
有用功相同时,希望额外功多好还是少好?
请算出几种种办法中有用功在总功中占的百分比。
19%
77%
87%
83%
机械效率
在使用机械工作时,有用功在总功中所占份额越多越好。它反映了机械的一种性能,物理学中表示为机械效率。
1.定义:有用功跟总功的比值。
2.公式:
机械效率
3.理解:a: η常用百分数表示;
b: η<100%;
c: η没有单位。
η读作“eta”
起重机的机械效率是60%
它表示什么意思?
使用起重机提升重物时所做的有用功跟总功的比值是60%,也可以说有用功在总功中占有60%,另外的40%是额外功。
机械效率的理解
1.有用功越多,机械效率越高 ( )
2.额外功越少,机械效率越高 ( )
3.物体做功越慢,机械效率越低 ( )
4.做总功越多,机械效率越低 ( )
5.做相同的有用功,额外功越少,机械效率越高 ( )
6.做相同的总功时,有用功越多,机械效率越高 ( )
7.用不同的滑轮组,做的有用功相同时,机械效率一定相同( )
8.因有用功总小于总功,所以机械效率总小于1 ( )
9.做的额外功一定时,总功越少,机械效率越高 ( )
10.有用功在总功中占的比例越大,机械效率越高 ( )
×
√
×
√
√
√
×
×
×
×
检测纠偏
例题:起重机把质量为0.6t的重物提升了3m,而它的电动机所做的功是3.4×104J,起重机的效率是多少?
检测纠偏
解: 起重机提升重物所用的力等于物体所受的重力:
F=G=mg=0.6 ×103 kg ×10 N / kg=6 × 103 N
起重机提升重物所做的功是有用功:
W有用 = Gh=6 × 103 N ×3m=1.8 × 104 J
起重机的电机所做的功是总功:
W总=3.4× 104J
起重机的机械效率是:
1.关于机械效率的说法中正确的是( )
A.越省力的机械,效率越高
B.做有用功越多的机械,效率越高
C.做相同的功,额外功的值越小,效率越高
D.做功越快的机械,效率越高
C
检测纠偏
2.如图,忽略绳重和摩擦,用拉力F拉着10 N的重物匀速上升,绳子自由端移动1 m,动滑轮重力2 N,求:
(1)拉力F;
(2)物体上升的距离;
(3)有用功,总功,机械效率。
检测纠偏
2.如图,忽略绳重和摩擦,用拉力F拉着10 N的重物匀速上升,绳子自由端移动1m,动滑轮重力2N,求:
(1)拉力F;
(2)物体上升的距离;
检测纠偏
n = 2,S = 1m
解:
2.如图,忽略绳重和摩擦,用拉力F拉着10 N的重物匀速上升,绳子自由端移动1m,动滑轮重力2N,求:
(3)有用功,总功,机械效率。
检测纠偏
解:
≈ 83.3%
方法二:
3.用一滑轮组将一重为2240N的货物匀速提起,所用向上的拉力为800N,不计阻力,此时机械效率为70%,则滑轮组应由( )
A、2个定滑轮,3个动滑轮组成
B、2个定滑轮,2个动滑轮组成
C、1个定滑轮,2个动滑轮组成
D、1个定滑轮,1个动滑轮组成
检测纠偏
C
一、有用功和额外功
1、有用功(W有)、额外功(W额)、总功(W总)
2、 W总= W有+ W额
二、机械效率(η)
1、概念:有用功跟总功的比值叫机械效率。
2、公式:
3、当W有一定时,W额越小, η 越高
三、斜面的机械效率
光滑程度一样的斜面,斜面越陡,机械效率越高;斜面越缓,机械效率越低。
倾斜程度一样的斜面,越光滑,机械效率越高;越粗糙,机械效率越低。
知识小结
12.3
课前回顾
1、什么是功?
2、功的计算式是什么?
3、你如何理解功的原理?
教学目标
1、了解什么是“有用功”、“额外
功”和“总功”。
2、理解什么是“机械效率”。
1、“效率”这个词大家并不陌生,谁能给大家解释一下?
2、机械帮助我们做功也会涉及效率问题,我们称为机械效率,要研究机械效率就要先研究使用机械效率做功的情况
情景导入
直接提升物体做功,与使用机械提升物体做功相同吗?
问题探究
G/N
h/m
W直/J
F/N
s/m
W机/J
2
0.1
0.2
1.2
0.2
0.24
结论:使用动滑轮比直接提升物体不省功。
推论:使用任何机械不省功。
实验
G/N
h/m
W直/J
F/N
s/m
W机/J
2
0.1
0.2
1.2
0.2
0.24
额外功:由于机械自重和摩擦等因素影响,
而不得不做的功(无用付出)。
有用功:直接对物体所做的功(工作目的)。
总功:利用机械所做的功(实际付出)。
概念
想一想:有哪些办法可以将沙子运上三楼?
有用功、额外功、总功
①
3克服自重做功
1对砂子做功
2对桶做功
②
1对砂子做功
2对桶做功
③
1对砂子做功
2对桶做功
3对动滑轮做功
④
1对砂子做功
2对口袋做功
3对动滑轮做功
思考:提升物体的过程中动力(人)对哪些物体做了功?
有用功概念:
满足我们做功的目的,对我们有价值的功,
计作:W有用
对重物(沙子)做的功
①
3克服自重做功
1对砂子做功
2对桶做功
②
1对砂子做功
2对桶做功
③
1对砂子做功
2对桶做功
3对动滑轮做功
④
1对砂子做功
2对口袋做功
3对动滑轮做功
问题1:哪些功达到了我们做功的目的?
1.桶、动滑轮、口袋等也随重物一起上升,也提升了它们,克服这些重力做的功。
2.此外,机械运转时都有摩擦克服机械的摩擦做的功。
额外功概念:
对我们既无利用价值而又不得不做的功。
计作:W额外
问题2:哪些功对我们没有价值,但又不得不做的功?
①
3克服自重做功
1对砂子做功
2对桶做功
②
1对砂子做功
2对桶做功
③
1对砂子做功
2对桶做功
3对动滑轮做功
④
1对砂子做功
2对口袋做功
3对动滑轮做功
三种功的计算
1、有用功(W有):对人们有用的功。
计算:提升物体(克服物重做功):W有=Gh
水平匀速(克服摩擦做功):W有=fS
2 、额外功(W额):人们不需要但又不得不做的功。
计算:提升物体(只计动滑轮重):W额=G动h
斜 面(克服摩擦做的功):W额=fL
3 、总功(W总):有用功与额外功的总和
(运用机械时动力F所做的功)。
计算:滑轮组:W总=FS [ F=(G+G动)/n;S=nh ];
斜 面:W总 =FL
4 、三者关系: W总= W有+ W额
1、用水桶从井中提水时,
所做的有用功是 ,
额外功是 ,
总功是 ;
2、如果桶掉到井里,从井里捞桶时,捞上来的桶里带了一些水,有用功是 ,
额外功是 ,
总功是 。
克服水的重力做功
克服桶的重力做功
拉力所做的功
克服桶的重力做功
克服水的重力做功
拉力所做的功
点拨释疑
算一算:算出有用功,额外功 总功分别是多少?
砂子重100N;桶重20N;人重400N;地面到三楼高6m
总功
=3120J
算一算:算出有用功,额外功 总功分别是多少?
1、对砂子做功(有用功)
W砂=G砂h=100N×6m=600J
2、对桶做功(额外功)
W桶=G桶h=20N×6m=120J
3、克服自重做功(额外功)
W人=G人h=400N×6m=2400J
砂子重100N;桶重20N;地面到三楼高6m
算一算:算出有用功,额外功 总功分别是多少?
总功
=720J
1、对砂子做功(有用功)
W砂=G砂h=100N×6m=600J
2、对桶做功(额外功)
W桶=G桶h=20N×6m=120J
砂子重100N;桶重20N;动滑轮重10N;地面到三楼高6m
算一算:算出有用功,额外功 总功分别是多少?
总功
=780J
1、对砂子做功(有用功)
W砂=G砂h=100N×6m=600J
2、对桶做功(额外功)
W桶=G桶h=20N×6m=120J
3、对滑轮做功(额外功)
W人=G滑h=10N×6m=60J
砂子重100N;动滑轮重10N;口袋重5N;地面到三楼高6m
算一算:算出有用功,额外功 总功分别是多少?
总功
=690J
1、对砂子做功(有用功)
W砂=G砂h=100N×6m=600J
2、对口袋做功(额外功)
W桶=G袋h=5N×6m=30J
3、对动滑轮做功(额外功)
W人=G滑h=10N×6m=60J
有用功相同时,希望额外功多好还是少好?
请算出几种种办法中有用功在总功中占的百分比。
19%
77%
87%
83%
机械效率
在使用机械工作时,有用功在总功中所占份额越多越好。它反映了机械的一种性能,物理学中表示为机械效率。
1.定义:有用功跟总功的比值。
2.公式:
机械效率
3.理解:a: η常用百分数表示;
b: η<100%;
c: η没有单位。
η读作“eta”
起重机的机械效率是60%
它表示什么意思?
使用起重机提升重物时所做的有用功跟总功的比值是60%,也可以说有用功在总功中占有60%,另外的40%是额外功。
机械效率的理解
1.有用功越多,机械效率越高 ( )
2.额外功越少,机械效率越高 ( )
3.物体做功越慢,机械效率越低 ( )
4.做总功越多,机械效率越低 ( )
5.做相同的有用功,额外功越少,机械效率越高 ( )
6.做相同的总功时,有用功越多,机械效率越高 ( )
7.用不同的滑轮组,做的有用功相同时,机械效率一定相同( )
8.因有用功总小于总功,所以机械效率总小于1 ( )
9.做的额外功一定时,总功越少,机械效率越高 ( )
10.有用功在总功中占的比例越大,机械效率越高 ( )
×
√
×
√
√
√
×
×
×
×
检测纠偏
例题:起重机把质量为0.6t的重物提升了3m,而它的电动机所做的功是3.4×104J,起重机的效率是多少?
检测纠偏
解: 起重机提升重物所用的力等于物体所受的重力:
F=G=mg=0.6 ×103 kg ×10 N / kg=6 × 103 N
起重机提升重物所做的功是有用功:
W有用 = Gh=6 × 103 N ×3m=1.8 × 104 J
起重机的电机所做的功是总功:
W总=3.4× 104J
起重机的机械效率是:
1.关于机械效率的说法中正确的是( )
A.越省力的机械,效率越高
B.做有用功越多的机械,效率越高
C.做相同的功,额外功的值越小,效率越高
D.做功越快的机械,效率越高
C
检测纠偏
2.如图,忽略绳重和摩擦,用拉力F拉着10 N的重物匀速上升,绳子自由端移动1 m,动滑轮重力2 N,求:
(1)拉力F;
(2)物体上升的距离;
(3)有用功,总功,机械效率。
检测纠偏
2.如图,忽略绳重和摩擦,用拉力F拉着10 N的重物匀速上升,绳子自由端移动1m,动滑轮重力2N,求:
(1)拉力F;
(2)物体上升的距离;
检测纠偏
n = 2,S = 1m
解:
2.如图,忽略绳重和摩擦,用拉力F拉着10 N的重物匀速上升,绳子自由端移动1m,动滑轮重力2N,求:
(3)有用功,总功,机械效率。
检测纠偏
解:
≈ 83.3%
方法二:
3.用一滑轮组将一重为2240N的货物匀速提起,所用向上的拉力为800N,不计阻力,此时机械效率为70%,则滑轮组应由( )
A、2个定滑轮,3个动滑轮组成
B、2个定滑轮,2个动滑轮组成
C、1个定滑轮,2个动滑轮组成
D、1个定滑轮,1个动滑轮组成
检测纠偏
C
一、有用功和额外功
1、有用功(W有)、额外功(W额)、总功(W总)
2、 W总= W有+ W额
二、机械效率(η)
1、概念:有用功跟总功的比值叫机械效率。
2、公式:
3、当W有一定时,W额越小, η 越高
三、斜面的机械效率
光滑程度一样的斜面,斜面越陡,机械效率越高;斜面越缓,机械效率越低。
倾斜程度一样的斜面,越光滑,机械效率越高;越粗糙,机械效率越低。
知识小结
