8.1 第2课时 圆柱、圆锥、圆台、球、简单组合体 课件(共53张PPT)2020-2021年高一下学期数学人教A版(2019)必修第二册第八章
文档属性
| 名称 | 8.1 第2课时 圆柱、圆锥、圆台、球、简单组合体 课件(共53张PPT)2020-2021年高一下学期数学人教A版(2019)必修第二册第八章 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览











文档简介
第八章 §8.1 基本立体图形
第2课时 圆柱、圆锥、圆台、球、简单组合体
学习目标
XUE XI MU BIAO
1.了解圆柱、圆锥、圆台、球的定义.
2.掌握圆柱、圆锥、圆台、球的结构特征.
3.了解简单组合体的概念及结构特征.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 圆柱的结构特征
圆柱
图形及表示
定义:以 所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱
?
图中圆柱表示为圆柱O′O
相关概念:
圆柱的轴:_______
圆柱的底面: 的边旋转而成的圆面
圆柱的侧面: 的边旋转而成的曲面
圆柱侧面的母线:无论旋转到什么位置,________
的边
矩形的一边
旋转轴
垂直于轴
平行于轴
平行于轴
思考 圆柱的轴截面有_______个,它们______(填“全等”或“相似”),圆柱的母线有________条,它们与圆柱的高______.
无穷多
全等
无穷多
相等
知识点二 圆锥的结构特征
圆锥
图形及表示
定义:以直角三角形的 所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体
?
图中圆锥表示为圆锥SO
相关概念:
圆锥的轴:旋转轴
圆锥的底面:垂直于轴的边旋转而成的圆面
侧面:直角三角形的斜边旋转而成的曲面
母线:无论旋转到什么位置 ,不垂直于轴的边
一条直角边
思考 圆锥的轴截面有多少个?母线有多少条?圆锥顶点和底面圆周上任意一点的连线都是母线吗?
答案 圆锥的轴截面有无穷多个,母线有无穷多条,圆锥顶点和底面圆周上任意一点的连线都是母线.
知识点三 圆台的结构特征
圆台
图形及表示
定义:用 的平面去截圆锥,_______
之间的部分叫做圆台
?
图中圆台表示为圆台O′O
相关概念:
圆台的轴:旋转轴
圆台的底面:垂直于轴的边旋转一周所形成的圆面
圆台的侧面:不垂直于轴的边旋转一周所形成的曲面
母线:无论旋转到什么位置,不垂直于轴的边
平行于圆锥底面
底面与
截面
知识点四 球的结构特征
球
图形及表示
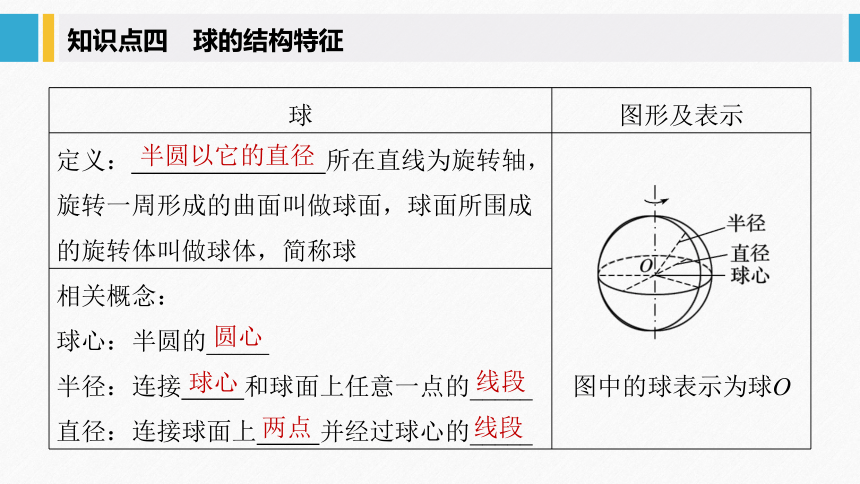
定义: 所在直线为旋转轴,旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称球
?
图中的球表示为球O
相关概念:
球心:半圆的_____
半径:连接 和球面上任意一点的_____
直径:连接球面上 并经过球心的_____
半圆以它的直径
圆心
球心
线段
两点
线段
知识点五 简单组合体的结构特征
1.概念:由 组合而成的,这些几何体叫做简单组合体.
2.基本形式:一种是由简单几何体 而成,另一种是由简单几何体 或 一部分而成.
简单几何体
拼接
截去
挖去
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.直角三角形绕一边所在直线旋转得到的旋转体是圆锥.( )
2.经过圆柱任意两条母线的截面都是一个矩形面.( )
3.球的直径是球面上任意两点所连线段的长.( )
4.半圆绕其直径所在直线旋转一周形成球.( )
×
√
×
×
2
题型探究
PART TWO
例1 下列说法正确的是______.(填序号)
①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;
②圆柱、圆锥、圆台的底面都是圆;
③以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋转一周形成的曲面所围成的几何体是圆锥;
④用一个平面去截球,得到的截面是一个圆面.
一、旋转体的结构特征
③④
解析 ①以直角梯形垂直于底边的一腰所在直线为轴旋转一周可得到圆台;
②它们的底面为圆面;
③④正确.
反思感悟
(1)判断简单旋转体结构特征的方法
①明确由哪个平面图形旋转而成.
②明确旋转轴是哪条直线.
(2)简单旋转体的轴截面及其应用
①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量.
②在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想.
跟踪训练1 (多选)下列说法,正确的是
A.圆柱的母线与它的轴可以不平行
B.圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的
连线都可以构成直角三角形
C.在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台
的母线
D.圆柱的任意两条母线所在直线是互相平行的
√
√
解析 由圆柱、圆锥、圆台的定义及母线的性质可知BD正确,AC错误.
二、简单组合体的结构特征
例2 请描述如图所示的几何体是如何形成的.
解 ①是由一个圆锥和一个圆台拼接而成的组合体;
②是由一个长方体截去一个三棱锥后得到的几何体;
③是由一个圆柱挖去一个三棱锥后得到的几何体.
反思感悟
判断组合体构成的方法
(1)判定实物图是由哪些简单几何体组成的问题时,首先要熟练掌握简单几何体的结构特征;其次要善于将复杂的组合体“分割”为几个简单的几何体.
(2)组合体是由简单几何体拼接或截去一部分构成的.要仔细观察组合体的构成,结合柱、锥、台、球的结构特征,先分割,后验证.
跟踪训练2 (1)如图所示的简单组合体的组成是
A.棱柱、棱台 B.棱柱、棱锥
C.棱锥、棱台 D.棱柱、棱柱
√
(2)将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括
A.一个圆台、两个圆锥 B.两个圆柱、一个圆锥
C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥
√
解析 图①是一个等腰梯形,CD为较长的底边,以CD边所在直线为旋转轴旋转一周所得几何体为一个组合体,如图②,包括一个圆柱、两个圆锥.
三、旋转体的有关计算
例3 已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同侧,且距离等于1,求这个球的半径.
解 如图,设这两个截面圆的半径分别为r1,r2,球心到截面的距离分别为d1,d2,球的半径为R,
即(d1-d2)(d1+d2)=3,
又d1-d2=1,
即球的半径等于3.
反思感悟
(1)用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中的经过旋转轴的截面(轴截面)的性质,利用相似三角形中的相似比,构设相关几何变量的方程(组)而得解.
(2)利用球的截面,将立体问题转化为平面问题是解决球的有关问题的关键.
跟踪训练3 如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台O′O的母线长.
解 设圆台的母线长为l cm,由截得的圆台上、下底面面积之比为1∶16,
可设截得的圆台的上、下底面的半径分别为r cm,4r cm.
过轴SO作截面,如图所示.
则△SO′A′∽△SOA,SA′=3 cm.
解得l=9,即圆台的母线长为9 cm.
3
随堂演练
PART THREE
1.(多选)下列说法中不正确的是
A.将正方形旋转不可能形成圆柱
B.夹在圆柱的两个平行截面间的几何体还是一个旋转体
C.圆锥截去一个小圆锥后剩余部分是圆台
D.通过圆台侧面上一点,有无数条母线
√
√
√
解析 将正方形绕其一边所在直线旋转可以形成圆柱,所以A错误;
B中没有说明这两个平行截面的位置关系,当这两个平行截面与底面平行时正确,其他情况下结论不一定正确,所以B错误;
通过圆台侧面上一点,只有一条母线,所以D错误.
1
2
3
4
5
1
2
3
4
5
2.下列选项中的三角形绕直线l旋转一周,能得到如图所示几何体的是
√
解析 由题意知,该几何体是组合体,上、下各一圆锥,显然B正确.
1
2
3
4
5
3.下面几何体的截面一定是圆面的是
A.圆台 B.球
C.圆柱 D.圆锥
√
解析 截面可以从各个不同的部位截取,截得的截面都是圆面的几何体只有球.
4.关于图中的组合体的结构特征有以下几种说法:
①由一个长方体挖去一个四棱柱构成;
②由一个长方体与两个四棱柱组合而成;
③由一个长方体挖去一个四棱台构成;
④由一个长方体与两个四棱台组合而成.
其中正确说法的序号是________.
1
2
3
4
5
①②
5.两相邻边长分别为3 cm和4 cm的矩形,以一边所在的直线为轴旋转所成的圆柱的底面积为_________ cm2.
1
2
3
4
5
16π或9π
解析 当以3 cm长的一边所在直线为轴旋转时,
得到的圆柱的底面半径为4 cm,底面积为16π cm2;
当以4 cm长的一边所在直线为轴旋转时,
得到的圆柱的底面半径为3 cm,底面积为9π cm2.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)圆柱、圆锥、圆台的结构特征.
(2)球的结构特征.
(3)简单组合体的结构特征.
2.方法归纳:分类讨论,转化与化归.
3.常见误区:同一平面图形以不同的轴旋转形成的旋转体一般是不同的.
4
课时对点练
PART FOUR
基础巩固
1.下列几何体中不是旋转体的是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
2.(多选)下列命题中正确的是
A.过球心的截面所截得的圆面的半径等于球的半径
B.母线长相等的不同圆锥的轴截面的面积相等
C.圆台中所有平行于底面的截面都是圆面
D.圆锥所有的轴截面都是全等的等腰三角形
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
3.如图所示的平面中阴影部分绕中间轴旋转一周,形成的几何体形状为
A.一个球体
B.一个球体中间挖去一个圆柱
C.一个圆柱
D.一个球体中间挖去一个长方体
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 圆面绕着直径所在的轴,旋转而形成球,矩形绕着轴旋转而形成圆柱. 故选B.
4.过球面上任意两点A,B作大圆,可能的个数是
A.有且只有一个 B.一个或无穷多个
C.无数个 D.以上均不正确
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 当过A,B的直线经过球心时,经过A,B的截面所得的圆都是球的大圆,这时过A,B作球的大圆有无数个;
当直线AB不经过球心O时,经过A,B,O的截面就是一个大圆,这时只能作出一个大圆.
5.用长为4,宽为2的矩形作侧面围成一个圆柱,此圆柱轴截面的面积为
√
解析 当围成的圆柱底面周长为4,高为2时,
设圆柱底面圆的半径为r,则2πr=4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.观察下列四个几何体,其中可看作是由两个棱柱组合而成的是______.
(填序号)
①④
解析 ①可看作由一个四棱柱和一个三棱柱组合而成,
④可看作由两个四棱柱组合而成.
7.已知一个圆柱的轴截面是一个正方形,且其面积是Q,则此圆柱的
底面半径为______.(用Q表示)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设圆柱的底面半径为r,则母线长为2r.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.一圆锥底面半径为2,母线长为6,将此圆锥沿一条母线展开,得到的扇形的面积为________.
12π
解析 因为圆锥的底面半径为2,
所以底面圆的周长为4π,
故将此圆锥沿一条母线展开,
9.一个圆锥的高为2 cm,母线与轴的夹角为30°,求圆锥的母线长及圆锥的轴截面的面积.
解 如图轴截面SAB,圆锥SO的底面直径为AB,SO为高,SA为母线,则∠ASO=30°.
在Rt△SOA中,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图所示,四边形ABCD绕边AD所在的直线EF旋转,其中AD∥BC,AD⊥CD.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,比较其不同点.
解 当AD>BC时,四边形ABCD绕EF旋转一周所得的
几何体是由底面半径为CD的圆柱和圆锥拼成的组合体,
当AD=BC时,四边形ABCD绕EF旋转一周所得的几何体是圆柱,
当AD1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.上、下底面面积分别为36π和49π,母线长为5的圆台,其两底面之间的距离为
√
解析 圆台的母线长l、高h和上、下两底面圆的半径r,R满足关系式l2=h2+(R-r)2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.如果圆锥的侧面展开图是直径为a的半圆面,那么此圆锥的轴截面是
A.等边三角形
B.等腰直角三角形
C.顶角为30°的等腰三角形
D.其他等腰三角形
√
解析 因为圆锥的侧面展开图是直径为a的半圆面,
所以此圆锥的轴截面是等边三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(多选)如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
解析 一个圆柱挖去一个圆锥后,剩下的几何体被一个竖直的平面所截后,圆柱的轮廓是矩形除去一条边,圆锥的轮廓是三角形除去一条边或抛物线的一部分.
14.如图所示的立体图形可由平面图形________绕轴旋转而成.
③④
解析 题图中的半球可由③绕轴旋转一周而成,
也可由④绕轴旋转180°而成.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.如图,模块①~⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.
(1)若从模块⑥中拿掉一个小正方体,再从模块①~⑤中选出一个模块放到模块⑥上,使得模块⑥成为长方体,则①~⑤中选出的模块可以是_____________(答案不唯一).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
①(或②或⑤)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由图可知,①~⑤中选出的一个模块可以是①,也可以是②,也可以是⑤.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若从模块①~⑤中选出3个放到模块⑥上,使模块⑥成为棱长为3的大正方体,则选出的3个模块是_________________(答案不唯一).
①②⑤(或①④⑤)
解析 先补齐中间一层,只能用⑤,再补最上一层,则可用①②,也可用①④.
16.圆台的上、下底面半径分别为5 cm,10 cm,母线长AB=20 cm,从圆台母线AB的中点M拉一条绳子绕圆台侧面转到点A,求:
(1)绳子的最短长度;
解 如图所示,将侧面展开,绳子的最短长度为侧面展开图中AM的长度,
设OB=l,
则θ·l=2π×5,θ·(l+20)=2π×10,
∴OA=40 cm,OM=30 cm.
即绳子最短长度为50 cm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)在绳子最短时,上底圆周上的点到绳子的最短距离.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 作OQ⊥AM于点Q,交弧BB′于点P,
则PQ为所求的最短距离.
∵OA·OM=AM·OQ,∴OQ=24 cm.
故PQ=OQ-OP=24-20=4(cm),
即上底圆周上的点到绳子的最短距离为4 cm.
本课结束
第2课时 圆柱、圆锥、圆台、球、简单组合体
学习目标
XUE XI MU BIAO
1.了解圆柱、圆锥、圆台、球的定义.
2.掌握圆柱、圆锥、圆台、球的结构特征.
3.了解简单组合体的概念及结构特征.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 圆柱的结构特征
圆柱
图形及表示
定义:以 所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱
?
图中圆柱表示为圆柱O′O
相关概念:
圆柱的轴:_______
圆柱的底面: 的边旋转而成的圆面
圆柱的侧面: 的边旋转而成的曲面
圆柱侧面的母线:无论旋转到什么位置,________
的边
矩形的一边
旋转轴
垂直于轴
平行于轴
平行于轴
思考 圆柱的轴截面有_______个,它们______(填“全等”或“相似”),圆柱的母线有________条,它们与圆柱的高______.
无穷多
全等
无穷多
相等
知识点二 圆锥的结构特征
圆锥
图形及表示
定义:以直角三角形的 所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体
?
图中圆锥表示为圆锥SO
相关概念:
圆锥的轴:旋转轴
圆锥的底面:垂直于轴的边旋转而成的圆面
侧面:直角三角形的斜边旋转而成的曲面
母线:无论旋转到什么位置 ,不垂直于轴的边
一条直角边
思考 圆锥的轴截面有多少个?母线有多少条?圆锥顶点和底面圆周上任意一点的连线都是母线吗?
答案 圆锥的轴截面有无穷多个,母线有无穷多条,圆锥顶点和底面圆周上任意一点的连线都是母线.
知识点三 圆台的结构特征
圆台
图形及表示
定义:用 的平面去截圆锥,_______
之间的部分叫做圆台
?
图中圆台表示为圆台O′O
相关概念:
圆台的轴:旋转轴
圆台的底面:垂直于轴的边旋转一周所形成的圆面
圆台的侧面:不垂直于轴的边旋转一周所形成的曲面
母线:无论旋转到什么位置,不垂直于轴的边
平行于圆锥底面
底面与
截面
知识点四 球的结构特征
球
图形及表示
定义: 所在直线为旋转轴,旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称球
?
图中的球表示为球O
相关概念:
球心:半圆的_____
半径:连接 和球面上任意一点的_____
直径:连接球面上 并经过球心的_____
半圆以它的直径
圆心
球心
线段
两点
线段
知识点五 简单组合体的结构特征
1.概念:由 组合而成的,这些几何体叫做简单组合体.
2.基本形式:一种是由简单几何体 而成,另一种是由简单几何体 或 一部分而成.
简单几何体
拼接
截去
挖去
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.直角三角形绕一边所在直线旋转得到的旋转体是圆锥.( )
2.经过圆柱任意两条母线的截面都是一个矩形面.( )
3.球的直径是球面上任意两点所连线段的长.( )
4.半圆绕其直径所在直线旋转一周形成球.( )
×
√
×
×
2
题型探究
PART TWO
例1 下列说法正确的是______.(填序号)
①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;
②圆柱、圆锥、圆台的底面都是圆;
③以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋转一周形成的曲面所围成的几何体是圆锥;
④用一个平面去截球,得到的截面是一个圆面.
一、旋转体的结构特征
③④
解析 ①以直角梯形垂直于底边的一腰所在直线为轴旋转一周可得到圆台;
②它们的底面为圆面;
③④正确.
反思感悟
(1)判断简单旋转体结构特征的方法
①明确由哪个平面图形旋转而成.
②明确旋转轴是哪条直线.
(2)简单旋转体的轴截面及其应用
①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量.
②在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想.
跟踪训练1 (多选)下列说法,正确的是
A.圆柱的母线与它的轴可以不平行
B.圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的
连线都可以构成直角三角形
C.在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台
的母线
D.圆柱的任意两条母线所在直线是互相平行的
√
√
解析 由圆柱、圆锥、圆台的定义及母线的性质可知BD正确,AC错误.
二、简单组合体的结构特征
例2 请描述如图所示的几何体是如何形成的.
解 ①是由一个圆锥和一个圆台拼接而成的组合体;
②是由一个长方体截去一个三棱锥后得到的几何体;
③是由一个圆柱挖去一个三棱锥后得到的几何体.
反思感悟
判断组合体构成的方法
(1)判定实物图是由哪些简单几何体组成的问题时,首先要熟练掌握简单几何体的结构特征;其次要善于将复杂的组合体“分割”为几个简单的几何体.
(2)组合体是由简单几何体拼接或截去一部分构成的.要仔细观察组合体的构成,结合柱、锥、台、球的结构特征,先分割,后验证.
跟踪训练2 (1)如图所示的简单组合体的组成是
A.棱柱、棱台 B.棱柱、棱锥
C.棱锥、棱台 D.棱柱、棱柱
√
(2)将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括
A.一个圆台、两个圆锥 B.两个圆柱、一个圆锥
C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥
√
解析 图①是一个等腰梯形,CD为较长的底边,以CD边所在直线为旋转轴旋转一周所得几何体为一个组合体,如图②,包括一个圆柱、两个圆锥.
三、旋转体的有关计算
例3 已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同侧,且距离等于1,求这个球的半径.
解 如图,设这两个截面圆的半径分别为r1,r2,球心到截面的距离分别为d1,d2,球的半径为R,
即(d1-d2)(d1+d2)=3,
又d1-d2=1,
即球的半径等于3.
反思感悟
(1)用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中的经过旋转轴的截面(轴截面)的性质,利用相似三角形中的相似比,构设相关几何变量的方程(组)而得解.
(2)利用球的截面,将立体问题转化为平面问题是解决球的有关问题的关键.
跟踪训练3 如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台O′O的母线长.
解 设圆台的母线长为l cm,由截得的圆台上、下底面面积之比为1∶16,
可设截得的圆台的上、下底面的半径分别为r cm,4r cm.
过轴SO作截面,如图所示.
则△SO′A′∽△SOA,SA′=3 cm.
解得l=9,即圆台的母线长为9 cm.
3
随堂演练
PART THREE
1.(多选)下列说法中不正确的是
A.将正方形旋转不可能形成圆柱
B.夹在圆柱的两个平行截面间的几何体还是一个旋转体
C.圆锥截去一个小圆锥后剩余部分是圆台
D.通过圆台侧面上一点,有无数条母线
√
√
√
解析 将正方形绕其一边所在直线旋转可以形成圆柱,所以A错误;
B中没有说明这两个平行截面的位置关系,当这两个平行截面与底面平行时正确,其他情况下结论不一定正确,所以B错误;
通过圆台侧面上一点,只有一条母线,所以D错误.
1
2
3
4
5
1
2
3
4
5
2.下列选项中的三角形绕直线l旋转一周,能得到如图所示几何体的是
√
解析 由题意知,该几何体是组合体,上、下各一圆锥,显然B正确.
1
2
3
4
5
3.下面几何体的截面一定是圆面的是
A.圆台 B.球
C.圆柱 D.圆锥
√
解析 截面可以从各个不同的部位截取,截得的截面都是圆面的几何体只有球.
4.关于图中的组合体的结构特征有以下几种说法:
①由一个长方体挖去一个四棱柱构成;
②由一个长方体与两个四棱柱组合而成;
③由一个长方体挖去一个四棱台构成;
④由一个长方体与两个四棱台组合而成.
其中正确说法的序号是________.
1
2
3
4
5
①②
5.两相邻边长分别为3 cm和4 cm的矩形,以一边所在的直线为轴旋转所成的圆柱的底面积为_________ cm2.
1
2
3
4
5
16π或9π
解析 当以3 cm长的一边所在直线为轴旋转时,
得到的圆柱的底面半径为4 cm,底面积为16π cm2;
当以4 cm长的一边所在直线为轴旋转时,
得到的圆柱的底面半径为3 cm,底面积为9π cm2.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)圆柱、圆锥、圆台的结构特征.
(2)球的结构特征.
(3)简单组合体的结构特征.
2.方法归纳:分类讨论,转化与化归.
3.常见误区:同一平面图形以不同的轴旋转形成的旋转体一般是不同的.
4
课时对点练
PART FOUR
基础巩固
1.下列几何体中不是旋转体的是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
2.(多选)下列命题中正确的是
A.过球心的截面所截得的圆面的半径等于球的半径
B.母线长相等的不同圆锥的轴截面的面积相等
C.圆台中所有平行于底面的截面都是圆面
D.圆锥所有的轴截面都是全等的等腰三角形
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
3.如图所示的平面中阴影部分绕中间轴旋转一周,形成的几何体形状为
A.一个球体
B.一个球体中间挖去一个圆柱
C.一个圆柱
D.一个球体中间挖去一个长方体
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 圆面绕着直径所在的轴,旋转而形成球,矩形绕着轴旋转而形成圆柱. 故选B.
4.过球面上任意两点A,B作大圆,可能的个数是
A.有且只有一个 B.一个或无穷多个
C.无数个 D.以上均不正确
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 当过A,B的直线经过球心时,经过A,B的截面所得的圆都是球的大圆,这时过A,B作球的大圆有无数个;
当直线AB不经过球心O时,经过A,B,O的截面就是一个大圆,这时只能作出一个大圆.
5.用长为4,宽为2的矩形作侧面围成一个圆柱,此圆柱轴截面的面积为
√
解析 当围成的圆柱底面周长为4,高为2时,
设圆柱底面圆的半径为r,则2πr=4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.观察下列四个几何体,其中可看作是由两个棱柱组合而成的是______.
(填序号)
①④
解析 ①可看作由一个四棱柱和一个三棱柱组合而成,
④可看作由两个四棱柱组合而成.
7.已知一个圆柱的轴截面是一个正方形,且其面积是Q,则此圆柱的
底面半径为______.(用Q表示)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设圆柱的底面半径为r,则母线长为2r.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.一圆锥底面半径为2,母线长为6,将此圆锥沿一条母线展开,得到的扇形的面积为________.
12π
解析 因为圆锥的底面半径为2,
所以底面圆的周长为4π,
故将此圆锥沿一条母线展开,
9.一个圆锥的高为2 cm,母线与轴的夹角为30°,求圆锥的母线长及圆锥的轴截面的面积.
解 如图轴截面SAB,圆锥SO的底面直径为AB,SO为高,SA为母线,则∠ASO=30°.
在Rt△SOA中,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图所示,四边形ABCD绕边AD所在的直线EF旋转,其中AD∥BC,AD⊥CD.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,比较其不同点.
解 当AD>BC时,四边形ABCD绕EF旋转一周所得的
几何体是由底面半径为CD的圆柱和圆锥拼成的组合体,
当AD=BC时,四边形ABCD绕EF旋转一周所得的几何体是圆柱,
当AD
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.上、下底面面积分别为36π和49π,母线长为5的圆台,其两底面之间的距离为
√
解析 圆台的母线长l、高h和上、下两底面圆的半径r,R满足关系式l2=h2+(R-r)2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.如果圆锥的侧面展开图是直径为a的半圆面,那么此圆锥的轴截面是
A.等边三角形
B.等腰直角三角形
C.顶角为30°的等腰三角形
D.其他等腰三角形
√
解析 因为圆锥的侧面展开图是直径为a的半圆面,
所以此圆锥的轴截面是等边三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(多选)如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
解析 一个圆柱挖去一个圆锥后,剩下的几何体被一个竖直的平面所截后,圆柱的轮廓是矩形除去一条边,圆锥的轮廓是三角形除去一条边或抛物线的一部分.
14.如图所示的立体图形可由平面图形________绕轴旋转而成.
③④
解析 题图中的半球可由③绕轴旋转一周而成,
也可由④绕轴旋转180°而成.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.如图,模块①~⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.
(1)若从模块⑥中拿掉一个小正方体,再从模块①~⑤中选出一个模块放到模块⑥上,使得模块⑥成为长方体,则①~⑤中选出的模块可以是_____________(答案不唯一).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
①(或②或⑤)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由图可知,①~⑤中选出的一个模块可以是①,也可以是②,也可以是⑤.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若从模块①~⑤中选出3个放到模块⑥上,使模块⑥成为棱长为3的大正方体,则选出的3个模块是_________________(答案不唯一).
①②⑤(或①④⑤)
解析 先补齐中间一层,只能用⑤,再补最上一层,则可用①②,也可用①④.
16.圆台的上、下底面半径分别为5 cm,10 cm,母线长AB=20 cm,从圆台母线AB的中点M拉一条绳子绕圆台侧面转到点A,求:
(1)绳子的最短长度;
解 如图所示,将侧面展开,绳子的最短长度为侧面展开图中AM的长度,
设OB=l,
则θ·l=2π×5,θ·(l+20)=2π×10,
∴OA=40 cm,OM=30 cm.
即绳子最短长度为50 cm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)在绳子最短时,上底圆周上的点到绳子的最短距离.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 作OQ⊥AM于点Q,交弧BB′于点P,
则PQ为所求的最短距离.
∵OA·OM=AM·OQ,∴OQ=24 cm.
故PQ=OQ-OP=24-20=4(cm),
即上底圆周上的点到绳子的最短距离为4 cm.
本课结束
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
