第18章平行四边形 单元训练卷(Word版 含解析)
文档属性
| 名称 | 第18章平行四边形 单元训练卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 677.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 00:00:00 | ||
图片预览

文档简介
第18章平行四边形 单元训练卷
1.已知四边形ABCD是平行四边形,下列说法正确的有( )
①当AB=BC时,它是矩形
②AC⊥BD时,它是菱形
③当∠ABC=90°时,它是菱形
④当AC=BD时,它是正方形
A.①② B.② C.②④ D.③④
2.如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
3.已知平行四边形ABCD中,∠A+∠C=110°,则∠B的度数为( )
A.125° B.135° C.145° D.155°
4.如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为( )
A.12 B.11 C.10 D.9
5.如图,在?ABCD中,∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=6,BC=10,CF=4,则BE的长为( )
A.4 B.8 C.8 D.10
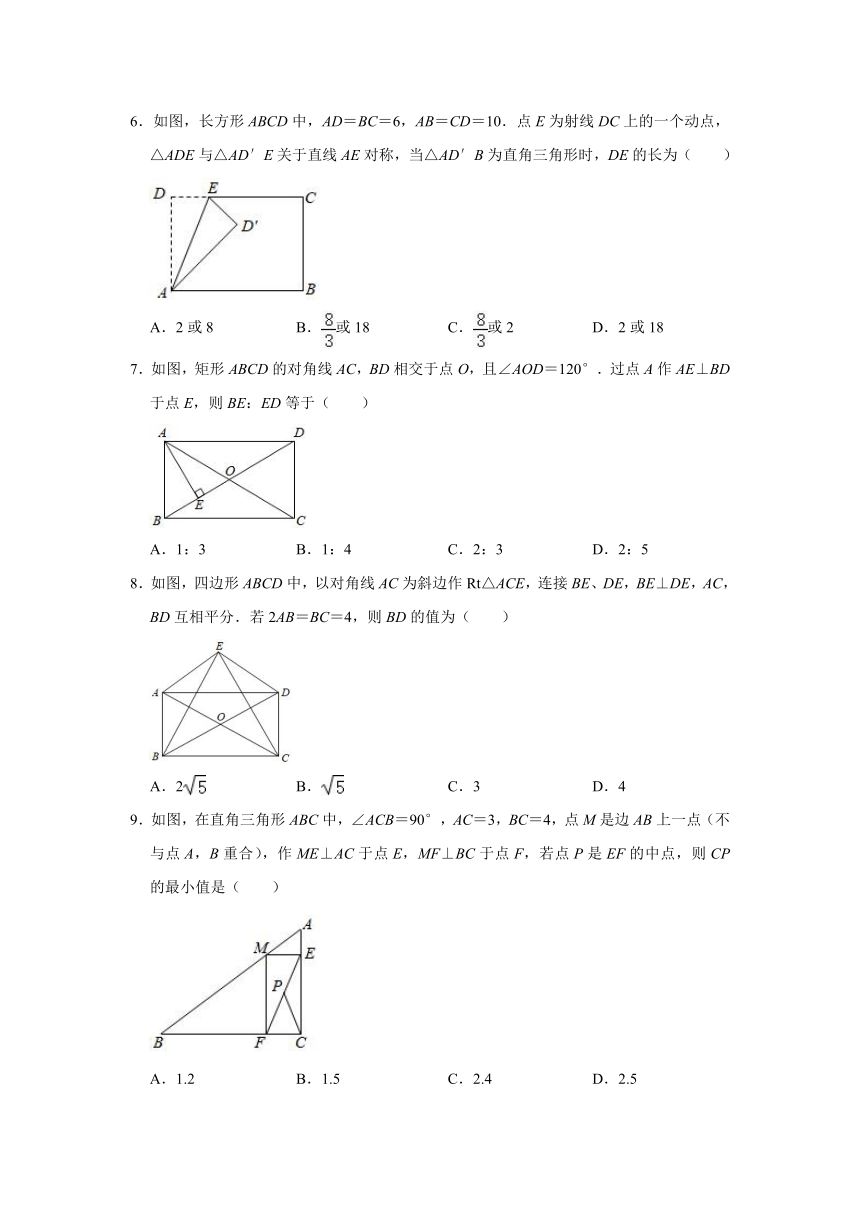
6.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
7.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
8.如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE、DE,BE⊥DE,AC,BD互相平分.若2AB=BC=4,则BD的值为( )
A.2 B. C.3 D.4
9.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
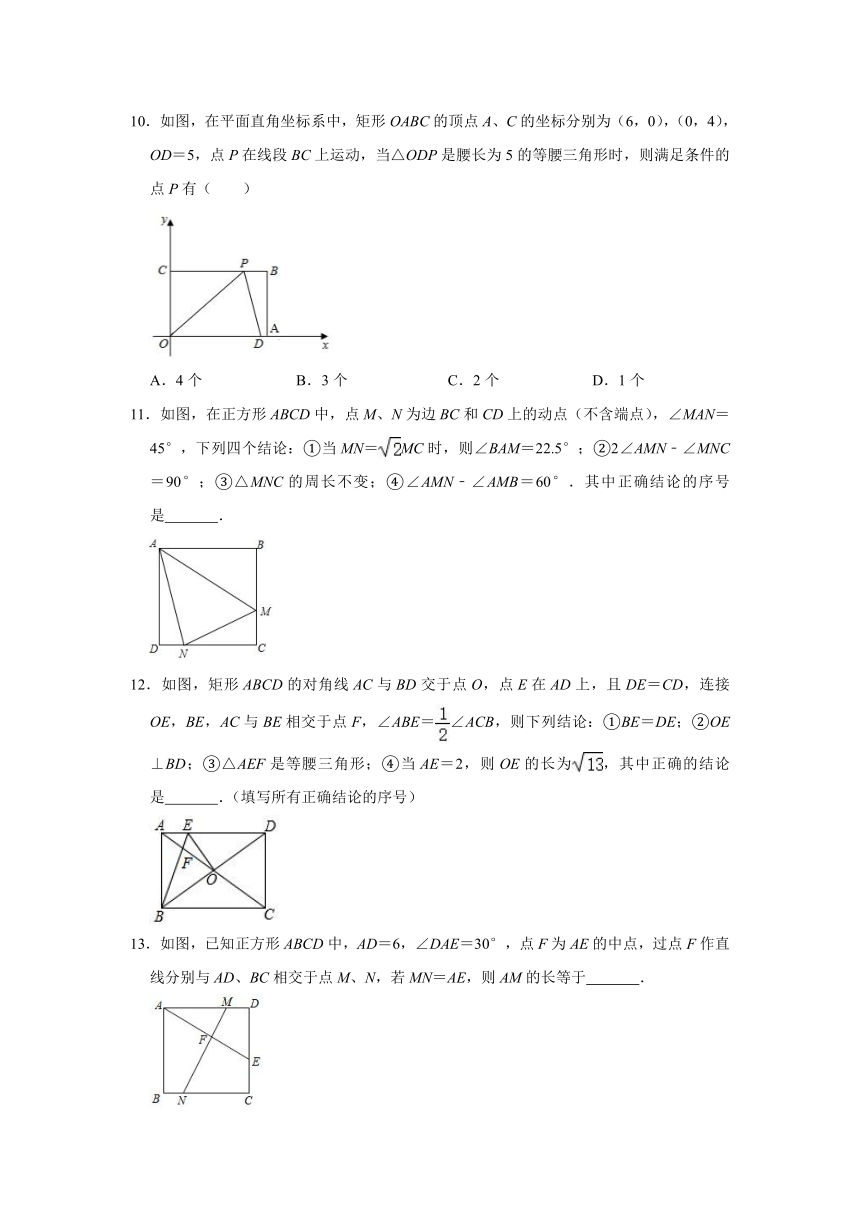
10.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0),(0,4),OD=5,点P在线段BC上运动,当△ODP是腰长为5的等腰三角形时,则满足条件的点P有( )
A.4个 B.3个 C.2个 D.1个
11.如图,在正方形ABCD中,点M、N为边BC和CD上的动点(不含端点),∠MAN=45°,下列四个结论:①当MN=MC时,则∠BAM=22.5°;②2∠AMN﹣∠MNC=90°;③△MNC的周长不变;④∠AMN﹣∠AMB=60°.其中正确结论的序号是 .
12.如图,矩形ABCD的对角线AC与BD交于点O,点E在AD上,且DE=CD,连接OE,BE,AC与BE相交于点F,∠ABE=∠ACB,则下列结论:①BE=DE;②OE⊥BD;③△AEF是等腰三角形;④当AE=2,则OE的长为,其中正确的结论是 .(填写所有正确结论的序号)
13.如图,已知正方形ABCD中,AD=6,∠DAE=30°,点F为AE的中点,过点F作直线分别与AD、BC相交于点M、N,若MN=AE,则AM的长等于 .
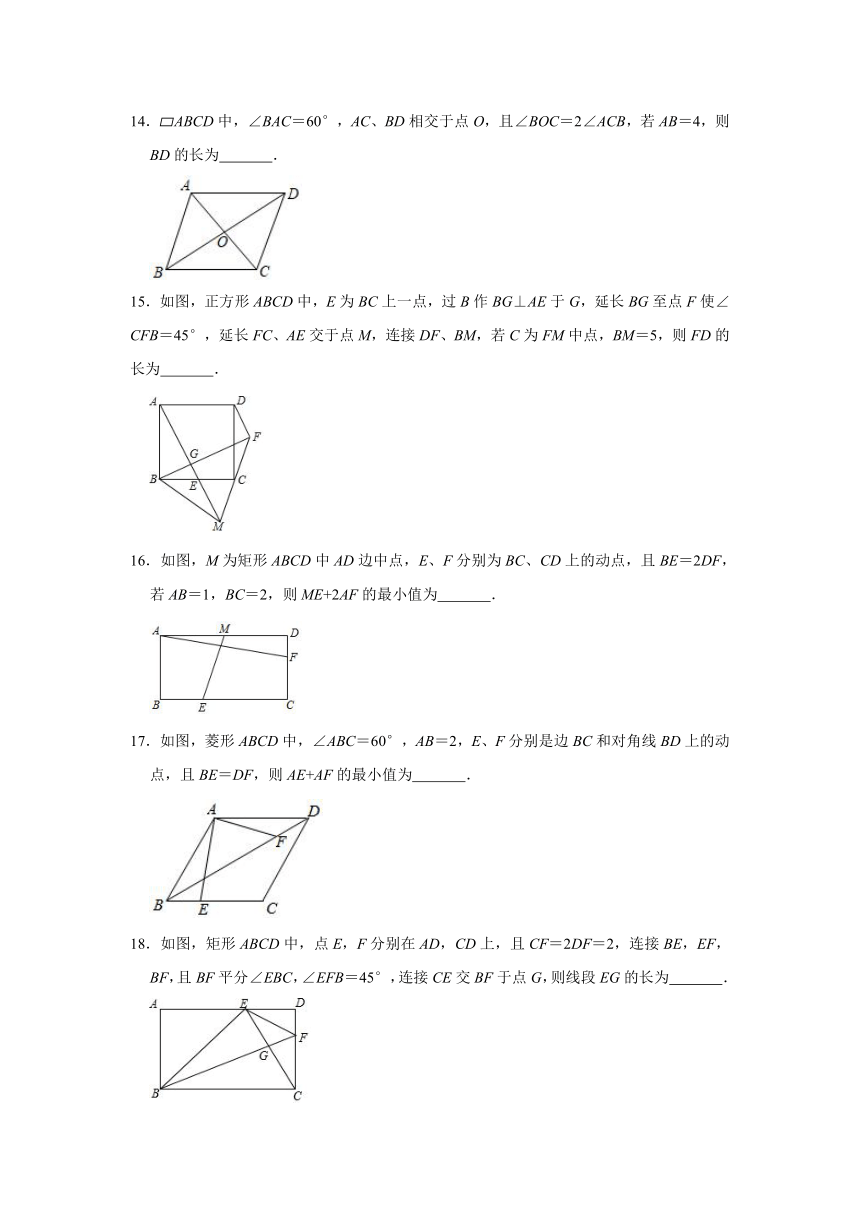
14.?ABCD中,∠BAC=60°,AC、BD相交于点O,且∠BOC=2∠ACB,若AB=4,则BD的长为 .
15.如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°,延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=5,则FD的长为 .
16.如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为 .
17.如图,菱形ABCD中,∠ABC=60°,AB=2,E、F分别是边BC和对角线BD上的动点,且BE=DF,则AE+AF的最小值为 .
18.如图,矩形ABCD中,点E,F分别在AD,CD上,且CF=2DF=2,连接BE,EF,BF,且BF平分∠EBC,∠EFB=45°,连接CE交BF于点G,则线段EG的长为 .
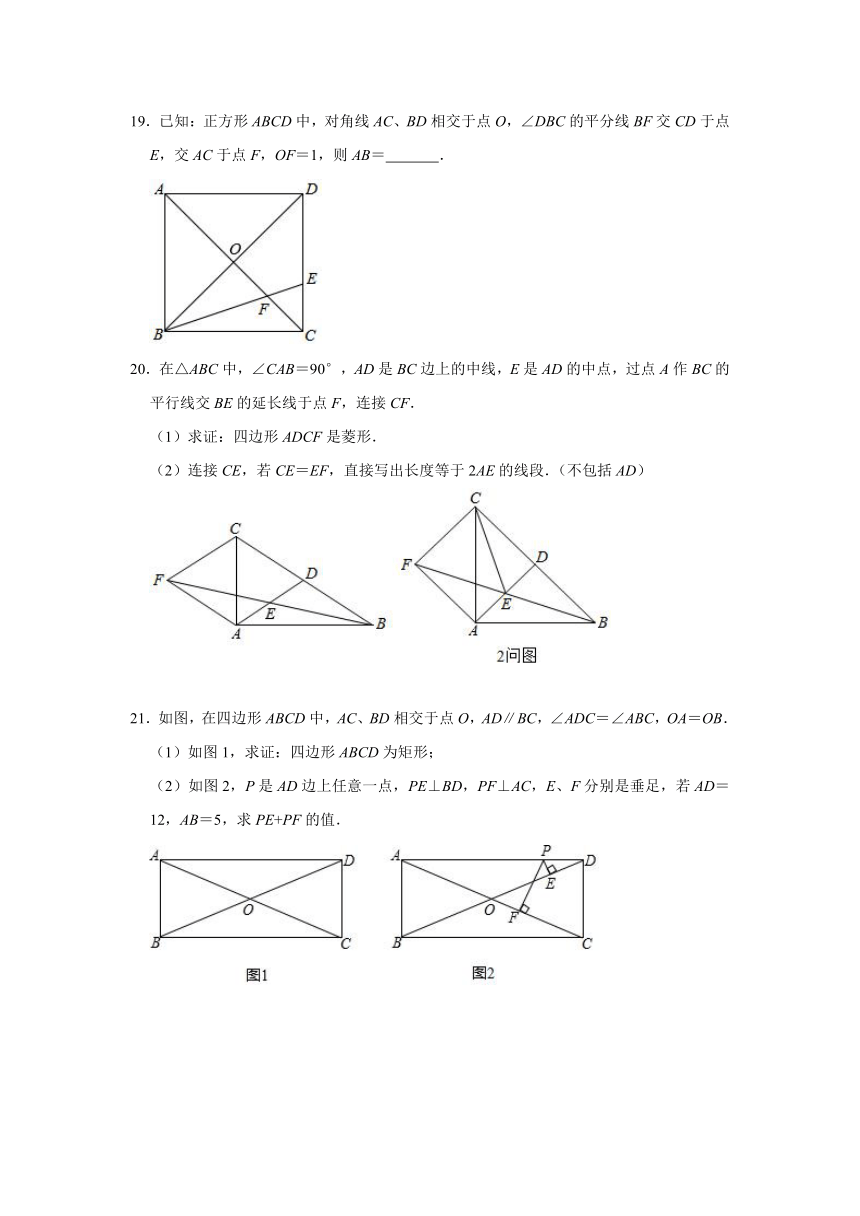
19.已知:正方形ABCD中,对角线AC、BD相交于点O,∠DBC的平分线BF交CD于点E,交AC于点F,OF=1,则AB= .
20.在△ABC中,∠CAB=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是菱形.
(2)连接CE,若CE=EF,直接写出长度等于2AE的线段.(不包括AD)
21.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
22.如图,已知正方形ABCD的边长为6,点E在CD边上,以线段CE为边长在正方形ABCD的外部作正方形CEFG,以线段AD和DE为邻边作矩形ADEH,若S正方形CEFG=S矩形ADEH.
(1)求线段CE的长;
(2)若点M为BC边的中点,连接MD,求证:MD=MG.
23.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:DE=CE.
(2)当EA⊥AB于点A,AE=ED=1时,求菱形的边长.
24.在四边形ABCD中,AB=BC,AD=CD,AC和BD交于点O,CE∥BD,DE∥AC,CE和DE交于点E.
(1)如图1,求证:四边形ODEC是矩形;
(2)如图2,连接OE,当AD∥BC时,在不添加任何辅助线及字母的情况下,请直接写出图中所有的平行四边形.
25.如图,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠A与∠DME之间的关系,并证明你的猜想.
(3)当∠BAC变为钝角时,如图②,上述(1)(2)中的结论是否都成立?若成立,直接回答,不需证明;若不成立,请说明理由.
26.如图,在?ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作?ECFG.
(1)证明?ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
27.如图1,△ABC是以∠ACB为直角的直角三角形,分别以AB,BC为边向外作正方形ABFG,BCED,连接AD,CF,AD与CF交于点M,AB与CF交于点N.
(1)求证:△ABD≌△FBC;
(2)如图2,在图1基础上连接AF和FD,若AD=6,求四边形ACDF的面积.
28.如图,已知正方形ABCD,点E在BC上,点F在CD延长线上,BE=DF
(1)求证:AE=AF;
(2)若BD与EF交于点M,连接AM,试判断AM与EF的数量与位置关系,并说明理由.
参考答案
1.解:①若AB=BC,则?ABCD是菱形,选项说法错误;
②若AC⊥BD,则?ABCD是菱形,选项说法正确;
③若∠ABC=90°,则?ABCD是矩形,选项说法错误;
④若AC=BD,则?ABCD是矩形,选项说法错误;
故选:B.
2.解:∵四边形ABCD是矩形,
∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,
∴DE=DC=2,
∴EC=2,
∵∠DCE=45°,
∴∠DEC=45°,
∵EB平分∠AEC,
∴∠AEC=∠AEC=,
∴∠BEC=180°﹣45°﹣67.5°=67.5°,
∴∠AEC=∠BEC,
∴BC=CE=2,
∴AD=BC=2,
∴AE=AD﹣DE=2﹣2,
故选:B.
3.解:∵四边形ABCD为平行四边形,∠A+∠C=110°,
∴∠A=∠C=55°,AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣55°=125°,
故选:A.
4.解:如图,延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=8,BN=ND,
又∵M是△ABC的边BC的中点,
∴MN是△BCD的中位线,
∴DC=2MN=4,
∴AC=AD+CD=8+4=12,
故选:A.
5.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,
∴∠EBC+∠FCB=∠ABC+∠DCB=90°,
∴EB⊥FC,
∴∠FGB=90°.
过A作AM∥FC,交BC于M,交BE于O,如图所示:
∵AM∥FC,
∴∠AOB=∠FGB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=6,
∵AO⊥BE,
∴BO=EO,
在△AOE和△MOB中,
,
∴△AOE≌△MOB(ASA),
∴AO=MO,
∵AF∥CM,AM∥FC,
∴四边形AMCF是平行四边形,
∴AM=FC=4,
∴AO=2,
∴EO===4,
∴BE=8.
故选:C.
6.解:分两种情况讨论:
①当E点在线段DC上时,
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵,AD'=AD,
∴BE=AB=10,
∵,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上时,如下图,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∵,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵,
∴DE=D″E=BD''+BE=8+10=18.
综上所知,DE=2或18.
故选:D.
7.解:∵四边形ABCD是矩形,
∴OA=OB=OD,
∵∠AOD=120°,
∴∠AOB=180°﹣120°=60°,
∴△AOB为等边三角形,
∵AE⊥BD,
∴BE=OE=OB,
∴ED=3BE,
∴=,
故选:A.
8.解:连接OE,如图所示:
∵2AB=BC=4,
∴AB=2,
∵AC,BD互相平分,
∴OA=OC,OB=OD,四边形ABCD是平行四边形,
∵以AC为斜边作Rt△ACE,
∴OE=OA=OC=AC,
∵BE⊥DE,
∴OE=OB=OD=BD,
∴AC=BD,
∴四边形ABCD是矩形,
∴AD=BC=4,∠BAD=90°,
∴BD===2,
故选:A.
9.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
10.解:由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如答图①所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD﹣DE=5﹣3=2,
∴此时点P坐标为(2,4);
(2)如答图②所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:OE===3,
∴此时点P坐标为(3,4);
(3)如答图③所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4)(舍弃).
综上所述,点P的坐标为:(2,4)或(3,4);
故选:C.
11.解:①:∵正方形ABCD中,AB=AD,∠B=∠ADC=∠C=90°
∴MN2=MC2+NC2
当MN=MC时,
MN2=2MC2,
∴MC2=NC2,
∴MC=NC,
∴BM=DN,
∴△ABM≌△ADN(SAS)
∴∠BAM=∠DAN,
∵∠MAN=45°,
∴∠BAM=22.5°,故①正确;
②:如图,将△ABM绕点A顺时针旋转90°得△ADE,
则∠EAN=∠EAM﹣∠MAN=90°﹣45°=45°,
则在△EAN和△MAN中,
,
∴△EAN≌△MAN(SAS)
∴∠AMN=∠AED,
∴∠AED+∠EAM+∠ENM+∠AMN=360°,
∴2∠AMN+90°+(180°﹣∠MNC)=360°,
∴2∠AMN﹣∠MNC=90°,
故②正确;
③:∵△EAN≌△MAN,
∴MN=EN=DE+DN=BM+DN,
∴△MNC的周长为:
MC+NC+MN=(MC+BM)+(NC+DN)=DC+BC,
∵DC和BC均为正方形ABCD的边长,故△MNC的周长不变.故③正确;
④如图,将△ADN绕点A逆时针旋转90°得△ABF,
∴∠MAF=90°﹣∠MAN=45°,
∴∠MAN=∠MAF,
在△MAN和△MAF中,
,
∴△MAN≌△MAF(SAS),
∴∠AMN=∠AMB,
故④错误.
综上①②③正确.
故答案为:①②③.
12.解:∵四边形ABCD是矩形,
∴AB=CD,∠BAE=90°,
∵DE=CD,
∴AB=DE,
∵AB<BE,
∴BE≠DE,故①错误;
∵BO=DO,BE≠DE,
∴OE与BD不垂直,故②错误;
如图,作CH⊥BE于H,EG⊥BD于G.设BE与AC的交点为F.
则∠HBC+∠BCH=∠BHC=90°,
∵四边形ABCD为矩形,
∴AD=BC,AB=CD,∠ABC=∠BAD=90°,AD∥BC,AC=BD
∴∠ABE+∠CBH=90°,
∴∠ABE=∠BCH,
∵∠ABE=∠ACB,
∴∠BCH=∠GCH,
∴BH=FH,BC=CG,∠CBH=∠CGH,
设AB=x,则ED=CD=AB=x,
∵AE=2,所以AD=AE+ED=2+x,
∴CG=CB=2+x,
∵AD∥BC,
∴∠AEG=∠CBH=∠CGH=∠AGE,
∴AF=AE=2,故③正确;
∴AC=AG+CG=4+x,
在Rt△ABC中:AB2+BC2=AC2,
∴x2+(x+2)2=(x+4)2,解得x1=6,x2=﹣2(舍),
∴AB=CD=6,AD=AC=8,AC=BD=10,
∵AC与BD交于点O,
∴AO=BO=CO=DO=5,
∵sin∠BDA===,cos∠BDA===,
∴EF=ED=,DF=ED=,
∴OF=OD﹣DF=5﹣=,
在Rt△EFO中:
OE2=OF2+EF2=()2+()2==13,
∴OE=,故④正确.
故其中正确的结论是③④.
故答案为:③④.
13.解:在正方形ABCD中,AD=6,∠DAE=30°,
设DE=x,则AE=2x,由勾股定理x2+62=(2x)2,
解得:x=2(负值舍去),
∴AE=4,
∵点F为AE的中点,
∴AF=EF=2,
分两种情况:
①过M作MG⊥BC,G为垂足,则MG=DC=AD,
在Rt△MGN和Rt△ADE中,
,
∴Rt△MGN≌Rt△ADE(HL),
∴∠NMG=∠EAD,
∴∠NMG+∠AMF=90°,
∴∠EAD+∠AMF=90°,
∴∠AFM=90°,
在Rt△AFM中,∠DAE=30°,AF=2,
设MF=m,则AM=2m,
由勾股定理,得
4m2﹣m2=12,
解得m=2(负值舍去),则AM=4;
②如图,过N作NG⊥AD于G,过M作MH⊥AE于H,
则NG=CD=AD,
在Rt△ADE和Rt△NGM中,
,
∴Rt△ADE≌Rt△NGM(HL),
∴∠GNM=∠DAE=30°,
∴∠GMN=60°,
△AMF中,∠GMN=∠MAF+∠AFM,
∴∠AFM=∠DAE=30°,
∴AM=MF,
∵MH⊥AF,
∴AH=FH,
设MH=x,则AM=2x,AH=FH=x,
∵F是AE的中点,
∴AE=2AF=4AH=4x,
Rt△ADE中,∠DAE=30°,
∴DE=AE=2x,AD=DE=6x,
∵AD=6,即6x=6,
x=1,即AM=2x=2;
故答案为:4或2.
14.解:如图,作BE⊥AC于点E,延长CE到点C′,使EC′=EC,连接BC′,
∴BE是CC′的垂直平分线,
∴BC=BC′,
∴∠C′=∠ACB,
∵∠BOC=∠C′BO+∠C′,
∴∠BOC=∠C′BO+∠ACB,
∵∠BOC=2∠ACB,
∴2∠ACB=∠C′BO+∠ACB,
∴∠ACB=∠C′BO,
∴∠C′=∠C′BO,
∴OB=OC′,
设OE=x,
∴C′E=CE=OE+OC=x+OC,
∴CC′=2CE=2(x+OC)=2x+2OC,
∵AC=2OC,
∴AC′=CC′﹣AC=2x,
∴OC′=AC′+OA=2x+OC,
∴OB=OC′=2x+OC,
在Rt△ABE中,∠BAE=60°,
∴∠ABE=30°,
∴AE=AB=2,BE=2,
∴OB=OC′=2+3x,
在Rt△OBE中,根据勾股定理,得
OB2=OE2+BE2,
∴(2+3x)2=x2+(2)2,
解得x=或x=﹣2(舍去),
∴OB=2+3x=,
∴BD=2OB=7.
故答案为:7.
15.解:如图,过C点作CH⊥BF于H点,过B点作BK⊥CM于K,过D作DQ⊥MF交MF延长线于Q.
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°,
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC(AAS),
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=GM,
∴BG=GM,
∵BM=5,
∴BG=,GM=2,
∴AG=2,AB=5,
∴HF=,
∴CF=×=,
∴CM=,
∵CK=CM=CF=,
∴BK=,
∵在△BKC和△CQD中,
∵∠CBK=∠DCQ,∠BKC=∠CQD=90°,BC=CD,
∴△BKC≌△CQD(AAS),
∴CQ=BK=,
DQ=CK=,
∴QF=CQ﹣CF=﹣=,
∴DQ=QF=,
∴DF=×=.
故答案为.
16.解:如图,过点M作MH⊥BC于H.设DF=x,则BE=2x.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,
∵MH⊥BC,
∴∠MHB=90°,
∴四边形ABHM是矩形,
∴AM=DM=BH=1,AB=MH=1,
∴EH=1﹣2x,
∴ME+2AF=+2=+,
欲求ME+2AF的最小值,相当于在x轴上找一点Q(2x,0),使得点Q到J(0,4),和K(1,1)的距离之和最小(如下图),
作点J关于x轴的对称点J′,连接KJ′交x轴于Q,连接JQ,此时JQ+QK的值最小,最小值=KJ′,
∵J′(0,﹣4),K(1,1),
∴KJ′==,
∴ME+2AF的最小值为,
故答案为.
17.解:如图,BC的下方作∠CBT=30°,在BT上截取BT,使得BT=AD,连接ET,AT.
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ADC=∠ABC=60°,∠ADF=∠ADC=30°,
∵AD=BT,∠ADF=∠TBE=30°,DF=BE,
∴△ADF≌△TBE(SAS),
∴AF=ET,
∵∠ABT=∠ABC+∠CBT=60°+30°=90°,AB=AD=BT=2,
∴AT===2,
∴AE+AF=AE+ET,
∵AE+ET≥AT,
∴AE+AF≥2,
∴AE+AF的最小值为2,
故答案为2.
18.解:在BC上截取BN,使BN=BE,过点G作GH⊥EF于点H,
∵BF平分∠EBC,
∴∠EBF=∠CBF,
又∵BE=BN,BF=BF,
∴△BEF≌△BNF(SAS),
∴EF=NF,∠EFB=∠NFB=45°,
∴∠EFN=90°,
∴∠EFD+∠NFC=90°,
又∵∠EFD+∠FED=90°,
∴∠NFC=∠FED,
又∵∠D=∠NCF=90°,
∴△NFC≌△FED(AAS),
∴ED=FC=2,
在Rt△FED中,DF=1,
∴EF===,
在Rt△EDC中,EC===,
设BN=BE=x,作GQ⊥BE于Q,GP⊥BC于P.
在Rt△ABE中,∵AB2+AE2=BE2,
∴32+(x﹣1)2=x2,
解得x=5,
∵BG平分∠EBC,GQ⊥BE,GP⊥BC,
∴GQ=GP,
∴==,
∴==,
∴EG=EC=,
故答案为.
19.解:如图作FH∥BC交BD于点H.
∵四边形ABCD是正方形,
∴∠OBC=∠OCB=45°,OB=OC,∠BOC=90°
∵FH∥BC,
∴∠OHF=∠OBC,∠OFH=∠OCB,
∴∠OHF=∠OFH,
∴OH=OF=1,FH==,
∵BF平分∠OBC,
∴∠HBF=∠FBC=∠BFH,
∴BH=FH=,
∴OB=OC=1+,
∴BC=OB=2+.
故答案为2+.
20.(1)证明:∵AF∥BC,
∴∠FAE=∠BDE,
又∵E为AD的中点,
∴AE=DE,
在△AEF和△DEB中,,
∴△AEF≌△DEB(ASA),
∴AF=BD,
∴四边形ADCF是平行四边形,
又∵∠CAB=90°,AD是BC边上的中点,
∴AD=BC=DC=BD,
∴?ADCF是菱形;
(2)解:长度等于2AE的线段为CD、CF、AF、DB(不包括AD),理由如下:
由(1)得:四边形ADCF是菱形,AD=BC=DC=BD,
∴AD=AF=CF=CD,
∴CD=CF=AF=BD=AD=2AE.
21.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
22.(1)解:设CE=x,则FG=EF=x,FH=6+x,
∵S正方形CEFG=S矩形ADEH,
∴S正方形CEFG+S矩形BCEH=S矩形BCEH+S矩形ADEH,
即S矩形BGFE=S正方形ABCD,
∴x(x+6)=36,解得x1=3﹣3,x2=﹣3﹣3(舍去),
即CE的长为3﹣3;
(2)证明:∵点M为BC边的中点,
∴MC=3,
在Rt△MCD中,DM==3,
∵MG=MC+CG=3+3﹣3=3,
∴MD=MG.
23.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
又∵AE=DE,
∴DE=CE.
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,BH=DH,AH=CH,
∴∠ABD=∠ADB,
∵AE═ED=1,
∴∠DAE=∠EDA,
∴∠DAE=∠ADE=∠ABD,
∵∠DAE+∠ADE+∠BAE+∠ABD=180°,
∴∠DAE=∠ADE=∠ABD=30°,
∴BE=2AE=2,
∴BD=BE+DE=3,
∴BH=DH=,
∵∠ABD=30°,AH⊥BD,
∴AB=2AH,BH=AH,
∴AH=,AB=2AH=,
即菱形的边长为.
24.(1)证明:∵AB=BC,AD=CD,
∴BD垂直平分AC,
∴∠COD=90°,
∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形,
∵∠COD=90°,
∴四边形ODEC是矩形;
(2)解:∵AB=BC,AD=CD,
∴BD垂直平分AC,
∴AO=OC,∠BOC=∠AOD,
∵AD∥BC,
∴∠BCO=∠DAO,
∴△AOD≌△COB(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形,
∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形,
∴DE=CO,
∴DE=AO,
∴四边形AOED是平行四边形,
∴AD=OE,AD∥OE,
∴BC=OE,BC∥OE,
∴四边形OECB是平行四边形,
综上所述,四边形ABCD,四边形ODEC,四边形AOED,四边形OECB是平行四边形.
25.(1)证明:如图(1),连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=BC,ME=BC,
∴DM=ME,
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB)
=360°﹣2(∠ABC+∠ACB)
=360°﹣2(180°﹣∠A)
=2∠A,
∴∠DME=180°﹣2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:连接DM,ME,
在△ABC中,∠ABC+∠ACB=180°﹣∠BAC,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC
=2(180°﹣∠BAC)
=360°﹣2∠BAC,
∴∠DME=180°﹣(360°﹣2∠BAC)
=2∠BAC﹣180°.
26.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DM=BD=5.
27.(1)证明:∵四边形ABFG和四边形BCED是正方形,
∴BC=BD,AB=BF,∠CBD=∠ABF=90°,
∴∠CBD+∠ABC=∠ABF+∠ABC,
∴∠ABD=∠CBF,
在△ABD和△FBC中
,
∴△ABD≌△FBC(SAS);
(2)解:∵△ABD≌△FBC,
∴∠BAD=∠BFC,AD=FC=6,
∴∠AMF=180°﹣(∠BAD+∠ANM)
=180°﹣(∠BFC+∠BNM)=180°﹣(180°﹣∠ABF)
=180°﹣(180°﹣90°)=90°,
即AD⊥CF,
∴四边形ACDF的面积S=S△ACD+S△ADF
=+===18.
28.(1)证明:∵四边形ABCD为正方形,
∴∠ABE=∠ADC=∠ADF=90°,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)AM⊥EF,AM=EF,理由是:
由(1)得:△ABE≌△ADF,
∴∠FAD=∠EAB,
∴∠FAE=∠DAB=90°,
∴△FAE是直角三角形,
如图,过E作EN∥CD,交BD于N,
∴∠MNE=∠MDF,∠MEN=∠MFD,
∵四边形ABCD为正方形,
∴∠NBE=45°,
∴△NBE是等腰直角三角形,
∴EN=BE=DF,
在△MNE和△MDF中,
∵,
∴△MNE≌△MDF(ASA),
∴EM=FM,
∵AE=AF,
∴AM⊥EF,AM=EF.
1.已知四边形ABCD是平行四边形,下列说法正确的有( )
①当AB=BC时,它是矩形
②AC⊥BD时,它是菱形
③当∠ABC=90°时,它是菱形
④当AC=BD时,它是正方形
A.①② B.② C.②④ D.③④
2.如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
3.已知平行四边形ABCD中,∠A+∠C=110°,则∠B的度数为( )
A.125° B.135° C.145° D.155°
4.如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为( )
A.12 B.11 C.10 D.9
5.如图,在?ABCD中,∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=6,BC=10,CF=4,则BE的长为( )
A.4 B.8 C.8 D.10
6.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
7.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
8.如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE、DE,BE⊥DE,AC,BD互相平分.若2AB=BC=4,则BD的值为( )
A.2 B. C.3 D.4
9.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
10.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0),(0,4),OD=5,点P在线段BC上运动,当△ODP是腰长为5的等腰三角形时,则满足条件的点P有( )
A.4个 B.3个 C.2个 D.1个
11.如图,在正方形ABCD中,点M、N为边BC和CD上的动点(不含端点),∠MAN=45°,下列四个结论:①当MN=MC时,则∠BAM=22.5°;②2∠AMN﹣∠MNC=90°;③△MNC的周长不变;④∠AMN﹣∠AMB=60°.其中正确结论的序号是 .
12.如图,矩形ABCD的对角线AC与BD交于点O,点E在AD上,且DE=CD,连接OE,BE,AC与BE相交于点F,∠ABE=∠ACB,则下列结论:①BE=DE;②OE⊥BD;③△AEF是等腰三角形;④当AE=2,则OE的长为,其中正确的结论是 .(填写所有正确结论的序号)
13.如图,已知正方形ABCD中,AD=6,∠DAE=30°,点F为AE的中点,过点F作直线分别与AD、BC相交于点M、N,若MN=AE,则AM的长等于 .
14.?ABCD中,∠BAC=60°,AC、BD相交于点O,且∠BOC=2∠ACB,若AB=4,则BD的长为 .
15.如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°,延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=5,则FD的长为 .
16.如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为 .
17.如图,菱形ABCD中,∠ABC=60°,AB=2,E、F分别是边BC和对角线BD上的动点,且BE=DF,则AE+AF的最小值为 .
18.如图,矩形ABCD中,点E,F分别在AD,CD上,且CF=2DF=2,连接BE,EF,BF,且BF平分∠EBC,∠EFB=45°,连接CE交BF于点G,则线段EG的长为 .
19.已知:正方形ABCD中,对角线AC、BD相交于点O,∠DBC的平分线BF交CD于点E,交AC于点F,OF=1,则AB= .
20.在△ABC中,∠CAB=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是菱形.
(2)连接CE,若CE=EF,直接写出长度等于2AE的线段.(不包括AD)
21.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
22.如图,已知正方形ABCD的边长为6,点E在CD边上,以线段CE为边长在正方形ABCD的外部作正方形CEFG,以线段AD和DE为邻边作矩形ADEH,若S正方形CEFG=S矩形ADEH.
(1)求线段CE的长;
(2)若点M为BC边的中点,连接MD,求证:MD=MG.
23.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:DE=CE.
(2)当EA⊥AB于点A,AE=ED=1时,求菱形的边长.
24.在四边形ABCD中,AB=BC,AD=CD,AC和BD交于点O,CE∥BD,DE∥AC,CE和DE交于点E.
(1)如图1,求证:四边形ODEC是矩形;
(2)如图2,连接OE,当AD∥BC时,在不添加任何辅助线及字母的情况下,请直接写出图中所有的平行四边形.
25.如图,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠A与∠DME之间的关系,并证明你的猜想.
(3)当∠BAC变为钝角时,如图②,上述(1)(2)中的结论是否都成立?若成立,直接回答,不需证明;若不成立,请说明理由.
26.如图,在?ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作?ECFG.
(1)证明?ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
27.如图1,△ABC是以∠ACB为直角的直角三角形,分别以AB,BC为边向外作正方形ABFG,BCED,连接AD,CF,AD与CF交于点M,AB与CF交于点N.
(1)求证:△ABD≌△FBC;
(2)如图2,在图1基础上连接AF和FD,若AD=6,求四边形ACDF的面积.
28.如图,已知正方形ABCD,点E在BC上,点F在CD延长线上,BE=DF
(1)求证:AE=AF;
(2)若BD与EF交于点M,连接AM,试判断AM与EF的数量与位置关系,并说明理由.
参考答案
1.解:①若AB=BC,则?ABCD是菱形,选项说法错误;
②若AC⊥BD,则?ABCD是菱形,选项说法正确;
③若∠ABC=90°,则?ABCD是矩形,选项说法错误;
④若AC=BD,则?ABCD是矩形,选项说法错误;
故选:B.
2.解:∵四边形ABCD是矩形,
∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,
∴DE=DC=2,
∴EC=2,
∵∠DCE=45°,
∴∠DEC=45°,
∵EB平分∠AEC,
∴∠AEC=∠AEC=,
∴∠BEC=180°﹣45°﹣67.5°=67.5°,
∴∠AEC=∠BEC,
∴BC=CE=2,
∴AD=BC=2,
∴AE=AD﹣DE=2﹣2,
故选:B.
3.解:∵四边形ABCD为平行四边形,∠A+∠C=110°,
∴∠A=∠C=55°,AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣55°=125°,
故选:A.
4.解:如图,延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=8,BN=ND,
又∵M是△ABC的边BC的中点,
∴MN是△BCD的中位线,
∴DC=2MN=4,
∴AC=AD+CD=8+4=12,
故选:A.
5.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,
∴∠EBC+∠FCB=∠ABC+∠DCB=90°,
∴EB⊥FC,
∴∠FGB=90°.
过A作AM∥FC,交BC于M,交BE于O,如图所示:
∵AM∥FC,
∴∠AOB=∠FGB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=6,
∵AO⊥BE,
∴BO=EO,
在△AOE和△MOB中,
,
∴△AOE≌△MOB(ASA),
∴AO=MO,
∵AF∥CM,AM∥FC,
∴四边形AMCF是平行四边形,
∴AM=FC=4,
∴AO=2,
∴EO===4,
∴BE=8.
故选:C.
6.解:分两种情况讨论:
①当E点在线段DC上时,
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵,AD'=AD,
∴BE=AB=10,
∵,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上时,如下图,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∵,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵,
∴DE=D″E=BD''+BE=8+10=18.
综上所知,DE=2或18.
故选:D.
7.解:∵四边形ABCD是矩形,
∴OA=OB=OD,
∵∠AOD=120°,
∴∠AOB=180°﹣120°=60°,
∴△AOB为等边三角形,
∵AE⊥BD,
∴BE=OE=OB,
∴ED=3BE,
∴=,
故选:A.
8.解:连接OE,如图所示:
∵2AB=BC=4,
∴AB=2,
∵AC,BD互相平分,
∴OA=OC,OB=OD,四边形ABCD是平行四边形,
∵以AC为斜边作Rt△ACE,
∴OE=OA=OC=AC,
∵BE⊥DE,
∴OE=OB=OD=BD,
∴AC=BD,
∴四边形ABCD是矩形,
∴AD=BC=4,∠BAD=90°,
∴BD===2,
故选:A.
9.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
10.解:由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如答图①所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD﹣DE=5﹣3=2,
∴此时点P坐标为(2,4);
(2)如答图②所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:OE===3,
∴此时点P坐标为(3,4);
(3)如答图③所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4)(舍弃).
综上所述,点P的坐标为:(2,4)或(3,4);
故选:C.
11.解:①:∵正方形ABCD中,AB=AD,∠B=∠ADC=∠C=90°
∴MN2=MC2+NC2
当MN=MC时,
MN2=2MC2,
∴MC2=NC2,
∴MC=NC,
∴BM=DN,
∴△ABM≌△ADN(SAS)
∴∠BAM=∠DAN,
∵∠MAN=45°,
∴∠BAM=22.5°,故①正确;
②:如图,将△ABM绕点A顺时针旋转90°得△ADE,
则∠EAN=∠EAM﹣∠MAN=90°﹣45°=45°,
则在△EAN和△MAN中,
,
∴△EAN≌△MAN(SAS)
∴∠AMN=∠AED,
∴∠AED+∠EAM+∠ENM+∠AMN=360°,
∴2∠AMN+90°+(180°﹣∠MNC)=360°,
∴2∠AMN﹣∠MNC=90°,
故②正确;
③:∵△EAN≌△MAN,
∴MN=EN=DE+DN=BM+DN,
∴△MNC的周长为:
MC+NC+MN=(MC+BM)+(NC+DN)=DC+BC,
∵DC和BC均为正方形ABCD的边长,故△MNC的周长不变.故③正确;
④如图,将△ADN绕点A逆时针旋转90°得△ABF,
∴∠MAF=90°﹣∠MAN=45°,
∴∠MAN=∠MAF,
在△MAN和△MAF中,
,
∴△MAN≌△MAF(SAS),
∴∠AMN=∠AMB,
故④错误.
综上①②③正确.
故答案为:①②③.
12.解:∵四边形ABCD是矩形,
∴AB=CD,∠BAE=90°,
∵DE=CD,
∴AB=DE,
∵AB<BE,
∴BE≠DE,故①错误;
∵BO=DO,BE≠DE,
∴OE与BD不垂直,故②错误;
如图,作CH⊥BE于H,EG⊥BD于G.设BE与AC的交点为F.
则∠HBC+∠BCH=∠BHC=90°,
∵四边形ABCD为矩形,
∴AD=BC,AB=CD,∠ABC=∠BAD=90°,AD∥BC,AC=BD
∴∠ABE+∠CBH=90°,
∴∠ABE=∠BCH,
∵∠ABE=∠ACB,
∴∠BCH=∠GCH,
∴BH=FH,BC=CG,∠CBH=∠CGH,
设AB=x,则ED=CD=AB=x,
∵AE=2,所以AD=AE+ED=2+x,
∴CG=CB=2+x,
∵AD∥BC,
∴∠AEG=∠CBH=∠CGH=∠AGE,
∴AF=AE=2,故③正确;
∴AC=AG+CG=4+x,
在Rt△ABC中:AB2+BC2=AC2,
∴x2+(x+2)2=(x+4)2,解得x1=6,x2=﹣2(舍),
∴AB=CD=6,AD=AC=8,AC=BD=10,
∵AC与BD交于点O,
∴AO=BO=CO=DO=5,
∵sin∠BDA===,cos∠BDA===,
∴EF=ED=,DF=ED=,
∴OF=OD﹣DF=5﹣=,
在Rt△EFO中:
OE2=OF2+EF2=()2+()2==13,
∴OE=,故④正确.
故其中正确的结论是③④.
故答案为:③④.
13.解:在正方形ABCD中,AD=6,∠DAE=30°,
设DE=x,则AE=2x,由勾股定理x2+62=(2x)2,
解得:x=2(负值舍去),
∴AE=4,
∵点F为AE的中点,
∴AF=EF=2,
分两种情况:
①过M作MG⊥BC,G为垂足,则MG=DC=AD,
在Rt△MGN和Rt△ADE中,
,
∴Rt△MGN≌Rt△ADE(HL),
∴∠NMG=∠EAD,
∴∠NMG+∠AMF=90°,
∴∠EAD+∠AMF=90°,
∴∠AFM=90°,
在Rt△AFM中,∠DAE=30°,AF=2,
设MF=m,则AM=2m,
由勾股定理,得
4m2﹣m2=12,
解得m=2(负值舍去),则AM=4;
②如图,过N作NG⊥AD于G,过M作MH⊥AE于H,
则NG=CD=AD,
在Rt△ADE和Rt△NGM中,
,
∴Rt△ADE≌Rt△NGM(HL),
∴∠GNM=∠DAE=30°,
∴∠GMN=60°,
△AMF中,∠GMN=∠MAF+∠AFM,
∴∠AFM=∠DAE=30°,
∴AM=MF,
∵MH⊥AF,
∴AH=FH,
设MH=x,则AM=2x,AH=FH=x,
∵F是AE的中点,
∴AE=2AF=4AH=4x,
Rt△ADE中,∠DAE=30°,
∴DE=AE=2x,AD=DE=6x,
∵AD=6,即6x=6,
x=1,即AM=2x=2;
故答案为:4或2.
14.解:如图,作BE⊥AC于点E,延长CE到点C′,使EC′=EC,连接BC′,
∴BE是CC′的垂直平分线,
∴BC=BC′,
∴∠C′=∠ACB,
∵∠BOC=∠C′BO+∠C′,
∴∠BOC=∠C′BO+∠ACB,
∵∠BOC=2∠ACB,
∴2∠ACB=∠C′BO+∠ACB,
∴∠ACB=∠C′BO,
∴∠C′=∠C′BO,
∴OB=OC′,
设OE=x,
∴C′E=CE=OE+OC=x+OC,
∴CC′=2CE=2(x+OC)=2x+2OC,
∵AC=2OC,
∴AC′=CC′﹣AC=2x,
∴OC′=AC′+OA=2x+OC,
∴OB=OC′=2x+OC,
在Rt△ABE中,∠BAE=60°,
∴∠ABE=30°,
∴AE=AB=2,BE=2,
∴OB=OC′=2+3x,
在Rt△OBE中,根据勾股定理,得
OB2=OE2+BE2,
∴(2+3x)2=x2+(2)2,
解得x=或x=﹣2(舍去),
∴OB=2+3x=,
∴BD=2OB=7.
故答案为:7.
15.解:如图,过C点作CH⊥BF于H点,过B点作BK⊥CM于K,过D作DQ⊥MF交MF延长线于Q.
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°,
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC(AAS),
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=GM,
∴BG=GM,
∵BM=5,
∴BG=,GM=2,
∴AG=2,AB=5,
∴HF=,
∴CF=×=,
∴CM=,
∵CK=CM=CF=,
∴BK=,
∵在△BKC和△CQD中,
∵∠CBK=∠DCQ,∠BKC=∠CQD=90°,BC=CD,
∴△BKC≌△CQD(AAS),
∴CQ=BK=,
DQ=CK=,
∴QF=CQ﹣CF=﹣=,
∴DQ=QF=,
∴DF=×=.
故答案为.
16.解:如图,过点M作MH⊥BC于H.设DF=x,则BE=2x.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,
∵MH⊥BC,
∴∠MHB=90°,
∴四边形ABHM是矩形,
∴AM=DM=BH=1,AB=MH=1,
∴EH=1﹣2x,
∴ME+2AF=+2=+,
欲求ME+2AF的最小值,相当于在x轴上找一点Q(2x,0),使得点Q到J(0,4),和K(1,1)的距离之和最小(如下图),
作点J关于x轴的对称点J′,连接KJ′交x轴于Q,连接JQ,此时JQ+QK的值最小,最小值=KJ′,
∵J′(0,﹣4),K(1,1),
∴KJ′==,
∴ME+2AF的最小值为,
故答案为.
17.解:如图,BC的下方作∠CBT=30°,在BT上截取BT,使得BT=AD,连接ET,AT.
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ADC=∠ABC=60°,∠ADF=∠ADC=30°,
∵AD=BT,∠ADF=∠TBE=30°,DF=BE,
∴△ADF≌△TBE(SAS),
∴AF=ET,
∵∠ABT=∠ABC+∠CBT=60°+30°=90°,AB=AD=BT=2,
∴AT===2,
∴AE+AF=AE+ET,
∵AE+ET≥AT,
∴AE+AF≥2,
∴AE+AF的最小值为2,
故答案为2.
18.解:在BC上截取BN,使BN=BE,过点G作GH⊥EF于点H,
∵BF平分∠EBC,
∴∠EBF=∠CBF,
又∵BE=BN,BF=BF,
∴△BEF≌△BNF(SAS),
∴EF=NF,∠EFB=∠NFB=45°,
∴∠EFN=90°,
∴∠EFD+∠NFC=90°,
又∵∠EFD+∠FED=90°,
∴∠NFC=∠FED,
又∵∠D=∠NCF=90°,
∴△NFC≌△FED(AAS),
∴ED=FC=2,
在Rt△FED中,DF=1,
∴EF===,
在Rt△EDC中,EC===,
设BN=BE=x,作GQ⊥BE于Q,GP⊥BC于P.
在Rt△ABE中,∵AB2+AE2=BE2,
∴32+(x﹣1)2=x2,
解得x=5,
∵BG平分∠EBC,GQ⊥BE,GP⊥BC,
∴GQ=GP,
∴==,
∴==,
∴EG=EC=,
故答案为.
19.解:如图作FH∥BC交BD于点H.
∵四边形ABCD是正方形,
∴∠OBC=∠OCB=45°,OB=OC,∠BOC=90°
∵FH∥BC,
∴∠OHF=∠OBC,∠OFH=∠OCB,
∴∠OHF=∠OFH,
∴OH=OF=1,FH==,
∵BF平分∠OBC,
∴∠HBF=∠FBC=∠BFH,
∴BH=FH=,
∴OB=OC=1+,
∴BC=OB=2+.
故答案为2+.
20.(1)证明:∵AF∥BC,
∴∠FAE=∠BDE,
又∵E为AD的中点,
∴AE=DE,
在△AEF和△DEB中,,
∴△AEF≌△DEB(ASA),
∴AF=BD,
∴四边形ADCF是平行四边形,
又∵∠CAB=90°,AD是BC边上的中点,
∴AD=BC=DC=BD,
∴?ADCF是菱形;
(2)解:长度等于2AE的线段为CD、CF、AF、DB(不包括AD),理由如下:
由(1)得:四边形ADCF是菱形,AD=BC=DC=BD,
∴AD=AF=CF=CD,
∴CD=CF=AF=BD=AD=2AE.
21.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
22.(1)解:设CE=x,则FG=EF=x,FH=6+x,
∵S正方形CEFG=S矩形ADEH,
∴S正方形CEFG+S矩形BCEH=S矩形BCEH+S矩形ADEH,
即S矩形BGFE=S正方形ABCD,
∴x(x+6)=36,解得x1=3﹣3,x2=﹣3﹣3(舍去),
即CE的长为3﹣3;
(2)证明:∵点M为BC边的中点,
∴MC=3,
在Rt△MCD中,DM==3,
∵MG=MC+CG=3+3﹣3=3,
∴MD=MG.
23.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
又∵AE=DE,
∴DE=CE.
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,BH=DH,AH=CH,
∴∠ABD=∠ADB,
∵AE═ED=1,
∴∠DAE=∠EDA,
∴∠DAE=∠ADE=∠ABD,
∵∠DAE+∠ADE+∠BAE+∠ABD=180°,
∴∠DAE=∠ADE=∠ABD=30°,
∴BE=2AE=2,
∴BD=BE+DE=3,
∴BH=DH=,
∵∠ABD=30°,AH⊥BD,
∴AB=2AH,BH=AH,
∴AH=,AB=2AH=,
即菱形的边长为.
24.(1)证明:∵AB=BC,AD=CD,
∴BD垂直平分AC,
∴∠COD=90°,
∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形,
∵∠COD=90°,
∴四边形ODEC是矩形;
(2)解:∵AB=BC,AD=CD,
∴BD垂直平分AC,
∴AO=OC,∠BOC=∠AOD,
∵AD∥BC,
∴∠BCO=∠DAO,
∴△AOD≌△COB(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形,
∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形,
∴DE=CO,
∴DE=AO,
∴四边形AOED是平行四边形,
∴AD=OE,AD∥OE,
∴BC=OE,BC∥OE,
∴四边形OECB是平行四边形,
综上所述,四边形ABCD,四边形ODEC,四边形AOED,四边形OECB是平行四边形.
25.(1)证明:如图(1),连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=BC,ME=BC,
∴DM=ME,
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB)
=360°﹣2(∠ABC+∠ACB)
=360°﹣2(180°﹣∠A)
=2∠A,
∴∠DME=180°﹣2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:连接DM,ME,
在△ABC中,∠ABC+∠ACB=180°﹣∠BAC,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC
=2(180°﹣∠BAC)
=360°﹣2∠BAC,
∴∠DME=180°﹣(360°﹣2∠BAC)
=2∠BAC﹣180°.
26.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DM=BD=5.
27.(1)证明:∵四边形ABFG和四边形BCED是正方形,
∴BC=BD,AB=BF,∠CBD=∠ABF=90°,
∴∠CBD+∠ABC=∠ABF+∠ABC,
∴∠ABD=∠CBF,
在△ABD和△FBC中
,
∴△ABD≌△FBC(SAS);
(2)解:∵△ABD≌△FBC,
∴∠BAD=∠BFC,AD=FC=6,
∴∠AMF=180°﹣(∠BAD+∠ANM)
=180°﹣(∠BFC+∠BNM)=180°﹣(180°﹣∠ABF)
=180°﹣(180°﹣90°)=90°,
即AD⊥CF,
∴四边形ACDF的面积S=S△ACD+S△ADF
=+===18.
28.(1)证明:∵四边形ABCD为正方形,
∴∠ABE=∠ADC=∠ADF=90°,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)AM⊥EF,AM=EF,理由是:
由(1)得:△ABE≌△ADF,
∴∠FAD=∠EAB,
∴∠FAE=∠DAB=90°,
∴△FAE是直角三角形,
如图,过E作EN∥CD,交BD于N,
∴∠MNE=∠MDF,∠MEN=∠MFD,
∵四边形ABCD为正方形,
∴∠NBE=45°,
∴△NBE是等腰直角三角形,
∴EN=BE=DF,
在△MNE和△MDF中,
∵,
∴△MNE≌△MDF(ASA),
∴EM=FM,
∵AE=AF,
∴AM⊥EF,AM=EF.
