人教版数学八年级下册:18.2.1 矩形 同步练习(2课时Word版附答案)
文档属性
| 名称 | 人教版数学八年级下册:18.2.1 矩形 同步练习(2课时Word版附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 148.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览




文档简介
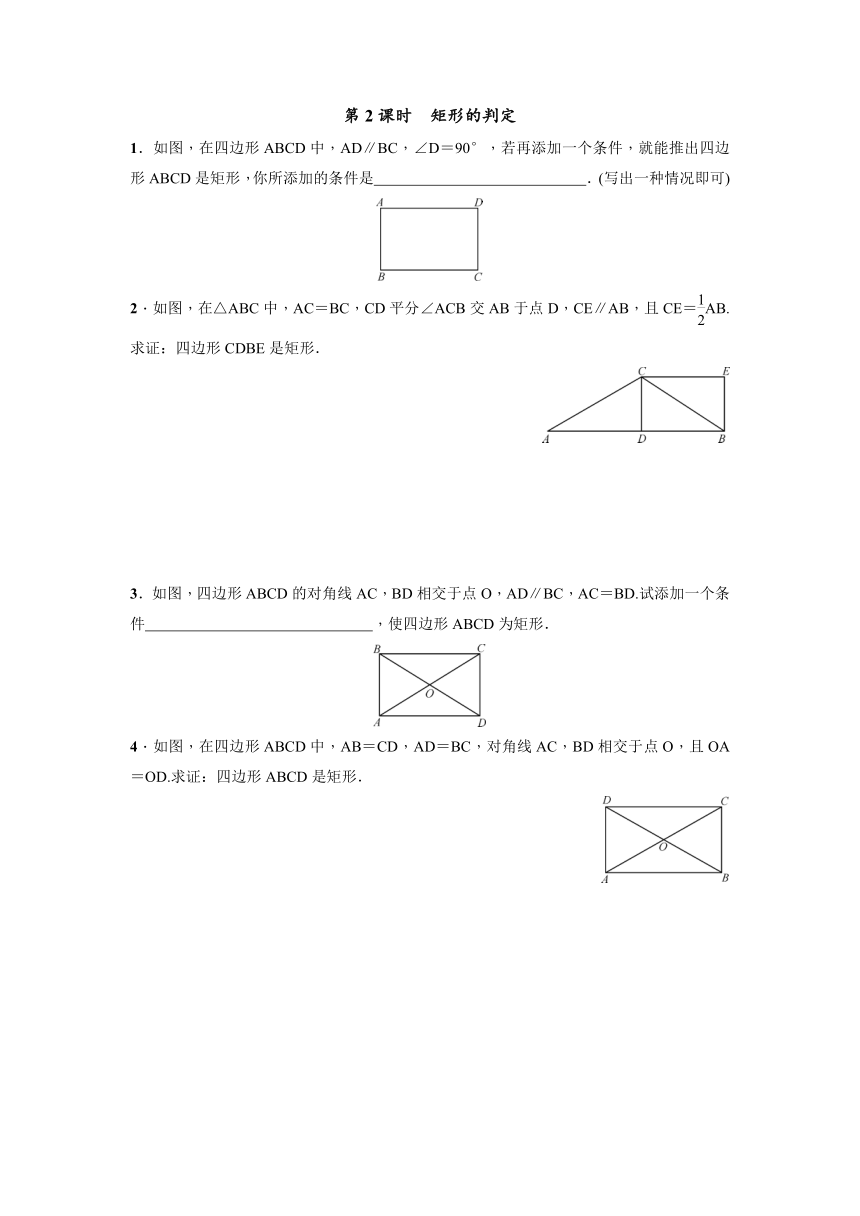
18.2.1 矩形
第1课时 矩形的性质
1.如图,在矩形ABCD中,对角线AC,BD相交于点O,以下说法错误的是( )
∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
2.如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是( )
A.8 B.6 C.4 D.2
3.如果矩形的一边长为6,一条对角线的长为10,那么这个矩形的另一边长是8.
4.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF.若AB=6 cm,BC=8 cm,则EF的长是 .
5.如图,在矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10.求:
42989500(1)矩形较短边的长;
(2)矩形较长边的长;
(3)矩形的面积.
6.如图,在Rt△ABC中,CD是斜边AB上的中线.若∠A=20°,则∠BDC=( )
A.30° B.40° C.45° D.60°
7.如图,在Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,则CD= .
8.如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于点H,FD=12,则HE等于( )
A.24 B.12 C.6 D.8
9.如图,矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于E.若OE∶ED=1∶3.AE=,则BD=( )
A.2 B.4 C.4 D.2
10.如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A.1 B. C.2 D.
11.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连接PB,PD.若AE=2,PF=8,则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
12.如图,已知矩形ABCD中,AB=3 cm,AD=9 cm,将此矩形折叠,使点B与点D重合,折痕为EF,求△ABE的面积.
13.如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF.求证:BF=CD.
14.如图,在矩形ABCD中,AB=3,BC=4.M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)求证:△ABM≌△CDN;
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
第2课时 矩形的判定
1.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是 .(写出一种情况即可)
2.如图,在△ABC中,AC=BC,CD平分∠ACB交AB于点D,CE∥AB,且CE=AB.求证:四边形CDBE是矩形.
3.如图,四边形ABCD的对角线AC,BD相交于点O,AD∥BC,AC=BD.试添加一个条件 ,使四边形ABCD为矩形.
4.如图,在四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
5.如图,在?ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.
6.下列命题正确的是( )
A.有一个角是直角的平行四边形是矩形
B.四条边相等的四边形是矩形
C.有一组邻边相等的平行四边形是矩形
D.对角线相等的四边形是矩形
7.如图,在平行四边形ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO
C.BD⊥AC D.∠AMB=∠CND
8.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
9.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为 .
10.如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.若AD=AF,求证:四边形ABFC是矩形.
11.如图,在四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若ED=EC,求证:EA=EG.
12.如图,在△ABC中,点Q是边AC上一个动点,过点Q作直线EF∥BC分别交∠ACB,外角∠ACD的平分线于点E,F.
(1)若CE=8,CF=6,求QC的长;
(2)连接AE,AF.问:当点Q在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
参考答案:
18.2.1 矩形
第1课时 矩形的性质
1.D
2.C
3. 8.
4.2.5_cm.
5.解:(1)∵四边形ABCD是矩形,∴OA=OB.
又∵∠AOB=60°,∴△AOB是等边三角形.
∴AB=OA=AC=5,即矩形较短边的长为5.
(2)在Rt△ABC中,∠ABC=90°,AB=5,AC=10,
则BC===5.
即矩形较长边的长是5.
(3)矩形的面积S=AB·BC=5×5=25.
6.B
7.3.
8.B
9.C
10.B
11.C
12.解:∵BE为ED所折,
∴BE=ED.∵AD=9,
设AE=x,则ED=BE=9-x,
在Rt△ABE中,AB=3,AE=x,BE=9-x.
∴BE2=AE2+AB2.
∴(9-x)2=x2+32.
∴x=4.
∴AE=4.
∴S△ABE=AB·AE=×3×4=6.
13.证明:∵四边形ABCD为矩形,∴∠B=∠C=90°.
∴∠BFE+∠BEF=90°.
∵EF⊥DF,∴∠DFE=90°.∴∠BFE+∠CFD=90°.
∴∠BEF=∠CFD.
在△BEF和△CFD中,
∴△BEF≌△CFD(ASA).
∴BF=CD.
14.解:(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD.
∴∠MAB=∠NCD.
在△ABM和△CDN中,
∴△ABM≌△CDN(SAS).
(2)连接EF,交AC于点O.
在△AEO和△CFO中,
∴△AEO≌△CFO(AAS).
∴EO=FO,AO=CO.
∴O为EF,AC中点.
∵∠EGF=90°,∴OG=EF=AB=.
在Rt△ABC中,AC==5,
∴OA=.
∴AG=OA-OG=1或AG=OA+OG=4.
∴AG的长为1或4.
第2课时 矩形的判定
1.答案不唯一,如:AD=BC或AB∥CD等.
2.证明:∵AC=BC,CD平分∠ACB交AB于点D,
∴CD⊥AB,AD=BD=AB.∴∠CDB=90°.
∵CE=AB,∴CE=BD.
∵CE∥AB,∴CE∥BD.
∴四边形CDBE为平行四边形.
又∵∠CDB=90°,
∴四边形CDBE是矩形.
3.答案不唯一,如:AB∥CD
4.证明:∵在四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
∴AC=2AO,BD=2OD.
∵OA=OD,
∴AC=BD.
∴四边形ABCD是矩形.
5.证明:∵四边形ABCD是平行四边形,
∴AB∥DC.
∴∠DAB+∠ADC=180°.
∵AF,DF分别是∠DAB,∠ADC的平分线,
∴∠FAD=∠BAE=∠DAB,
∠ADF=∠CDF=∠ADC.
∴∠FAD+∠FDA=90°.∴∠AFD=90°.
同理:∠BHC=∠HEF=90°.
∴∠AFD=∠BHC=∠HEF=90°.
∴四边形EFGH是矩形.
6.A
7.A
8. 12.
9..
10.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC.
∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E为BC的中点,∴EB=EC.
∴△ABE≌△FCE(AAS).∴AB=CF.
又∵AB∥CF,
∴四边形ABFC是平行四边形.
∵AD=BC,AD=AF,
∴BC=AF.
∴四边形ABFC是矩形.
11.证明:(1)∵AB∥DC,FC=AB,
∴四边形ABCF是平行四边形.
又∵∠B=90°,∴四边形ABCF是矩形.
(2)∵四边形ABCF是矩形,
∴∠AFC=∠AFD=90°.
∴∠DAF=90°-∠D,∠CGF=90°-∠ECD.
∵ED=EC,
∴∠D=∠ECD.
∴∠DAF=∠CGF.
又∵∠EGA=∠CGF,
∴∠DAF=∠EGA.
∴EA=EG.
12.解:(1)∵EF交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠QCE=∠BCE,∠QCF=∠DCF.
∵EF∥BC,
∴∠QEC=∠BCE,∠QFC=∠DCF.
∴∠QEC=∠QCE,∠QFC=∠QCF.
∴QE=QC,QF=QC.
∴QE=QF.
∵∠QCE+∠BCE+∠QCF+∠DCF=180°,
∴∠ECF=90°.
在Rt△CEF中,由勾股定理,得
EF==10,
∴QC=QE=EF=5.
(2)当点Q在边AC上运动到AC的中点时,四边形AECF是矩形.理由如下:
连接AE,AF.
当Q为AC的中点时,AQ=CQ,
∵EQ=FQ,
∴四边形AECF是平行四边形.
又∵∠ECF=90°,
∴四边形AECF是矩形.
第1课时 矩形的性质
1.如图,在矩形ABCD中,对角线AC,BD相交于点O,以下说法错误的是( )
∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
2.如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是( )
A.8 B.6 C.4 D.2
3.如果矩形的一边长为6,一条对角线的长为10,那么这个矩形的另一边长是8.
4.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF.若AB=6 cm,BC=8 cm,则EF的长是 .
5.如图,在矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10.求:
42989500(1)矩形较短边的长;
(2)矩形较长边的长;
(3)矩形的面积.
6.如图,在Rt△ABC中,CD是斜边AB上的中线.若∠A=20°,则∠BDC=( )
A.30° B.40° C.45° D.60°
7.如图,在Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,则CD= .
8.如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于点H,FD=12,则HE等于( )
A.24 B.12 C.6 D.8
9.如图,矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于E.若OE∶ED=1∶3.AE=,则BD=( )
A.2 B.4 C.4 D.2
10.如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A.1 B. C.2 D.
11.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连接PB,PD.若AE=2,PF=8,则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
12.如图,已知矩形ABCD中,AB=3 cm,AD=9 cm,将此矩形折叠,使点B与点D重合,折痕为EF,求△ABE的面积.
13.如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF.求证:BF=CD.
14.如图,在矩形ABCD中,AB=3,BC=4.M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)求证:△ABM≌△CDN;
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
第2课时 矩形的判定
1.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是 .(写出一种情况即可)
2.如图,在△ABC中,AC=BC,CD平分∠ACB交AB于点D,CE∥AB,且CE=AB.求证:四边形CDBE是矩形.
3.如图,四边形ABCD的对角线AC,BD相交于点O,AD∥BC,AC=BD.试添加一个条件 ,使四边形ABCD为矩形.
4.如图,在四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
5.如图,在?ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.
6.下列命题正确的是( )
A.有一个角是直角的平行四边形是矩形
B.四条边相等的四边形是矩形
C.有一组邻边相等的平行四边形是矩形
D.对角线相等的四边形是矩形
7.如图,在平行四边形ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO
C.BD⊥AC D.∠AMB=∠CND
8.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
9.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为 .
10.如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.若AD=AF,求证:四边形ABFC是矩形.
11.如图,在四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若ED=EC,求证:EA=EG.
12.如图,在△ABC中,点Q是边AC上一个动点,过点Q作直线EF∥BC分别交∠ACB,外角∠ACD的平分线于点E,F.
(1)若CE=8,CF=6,求QC的长;
(2)连接AE,AF.问:当点Q在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
参考答案:
18.2.1 矩形
第1课时 矩形的性质
1.D
2.C
3. 8.
4.2.5_cm.
5.解:(1)∵四边形ABCD是矩形,∴OA=OB.
又∵∠AOB=60°,∴△AOB是等边三角形.
∴AB=OA=AC=5,即矩形较短边的长为5.
(2)在Rt△ABC中,∠ABC=90°,AB=5,AC=10,
则BC===5.
即矩形较长边的长是5.
(3)矩形的面积S=AB·BC=5×5=25.
6.B
7.3.
8.B
9.C
10.B
11.C
12.解:∵BE为ED所折,
∴BE=ED.∵AD=9,
设AE=x,则ED=BE=9-x,
在Rt△ABE中,AB=3,AE=x,BE=9-x.
∴BE2=AE2+AB2.
∴(9-x)2=x2+32.
∴x=4.
∴AE=4.
∴S△ABE=AB·AE=×3×4=6.
13.证明:∵四边形ABCD为矩形,∴∠B=∠C=90°.
∴∠BFE+∠BEF=90°.
∵EF⊥DF,∴∠DFE=90°.∴∠BFE+∠CFD=90°.
∴∠BEF=∠CFD.
在△BEF和△CFD中,
∴△BEF≌△CFD(ASA).
∴BF=CD.
14.解:(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD.
∴∠MAB=∠NCD.
在△ABM和△CDN中,
∴△ABM≌△CDN(SAS).
(2)连接EF,交AC于点O.
在△AEO和△CFO中,
∴△AEO≌△CFO(AAS).
∴EO=FO,AO=CO.
∴O为EF,AC中点.
∵∠EGF=90°,∴OG=EF=AB=.
在Rt△ABC中,AC==5,
∴OA=.
∴AG=OA-OG=1或AG=OA+OG=4.
∴AG的长为1或4.
第2课时 矩形的判定
1.答案不唯一,如:AD=BC或AB∥CD等.
2.证明:∵AC=BC,CD平分∠ACB交AB于点D,
∴CD⊥AB,AD=BD=AB.∴∠CDB=90°.
∵CE=AB,∴CE=BD.
∵CE∥AB,∴CE∥BD.
∴四边形CDBE为平行四边形.
又∵∠CDB=90°,
∴四边形CDBE是矩形.
3.答案不唯一,如:AB∥CD
4.证明:∵在四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
∴AC=2AO,BD=2OD.
∵OA=OD,
∴AC=BD.
∴四边形ABCD是矩形.
5.证明:∵四边形ABCD是平行四边形,
∴AB∥DC.
∴∠DAB+∠ADC=180°.
∵AF,DF分别是∠DAB,∠ADC的平分线,
∴∠FAD=∠BAE=∠DAB,
∠ADF=∠CDF=∠ADC.
∴∠FAD+∠FDA=90°.∴∠AFD=90°.
同理:∠BHC=∠HEF=90°.
∴∠AFD=∠BHC=∠HEF=90°.
∴四边形EFGH是矩形.
6.A
7.A
8. 12.
9..
10.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC.
∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E为BC的中点,∴EB=EC.
∴△ABE≌△FCE(AAS).∴AB=CF.
又∵AB∥CF,
∴四边形ABFC是平行四边形.
∵AD=BC,AD=AF,
∴BC=AF.
∴四边形ABFC是矩形.
11.证明:(1)∵AB∥DC,FC=AB,
∴四边形ABCF是平行四边形.
又∵∠B=90°,∴四边形ABCF是矩形.
(2)∵四边形ABCF是矩形,
∴∠AFC=∠AFD=90°.
∴∠DAF=90°-∠D,∠CGF=90°-∠ECD.
∵ED=EC,
∴∠D=∠ECD.
∴∠DAF=∠CGF.
又∵∠EGA=∠CGF,
∴∠DAF=∠EGA.
∴EA=EG.
12.解:(1)∵EF交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠QCE=∠BCE,∠QCF=∠DCF.
∵EF∥BC,
∴∠QEC=∠BCE,∠QFC=∠DCF.
∴∠QEC=∠QCE,∠QFC=∠QCF.
∴QE=QC,QF=QC.
∴QE=QF.
∵∠QCE+∠BCE+∠QCF+∠DCF=180°,
∴∠ECF=90°.
在Rt△CEF中,由勾股定理,得
EF==10,
∴QC=QE=EF=5.
(2)当点Q在边AC上运动到AC的中点时,四边形AECF是矩形.理由如下:
连接AE,AF.
当Q为AC的中点时,AQ=CQ,
∵EQ=FQ,
∴四边形AECF是平行四边形.
又∵∠ECF=90°,
∴四边形AECF是矩形.
