人教版数学八年级下册:18.1.1 平行四边形的性质 同步练习(2课时Word版附答案)
文档属性
| 名称 | 人教版数学八年级下册:18.1.1 平行四边形的性质 同步练习(2课时Word版附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 163.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览



文档简介
18.1.1 平行四边形的性质
第1课时 平行四边形边、角的性质
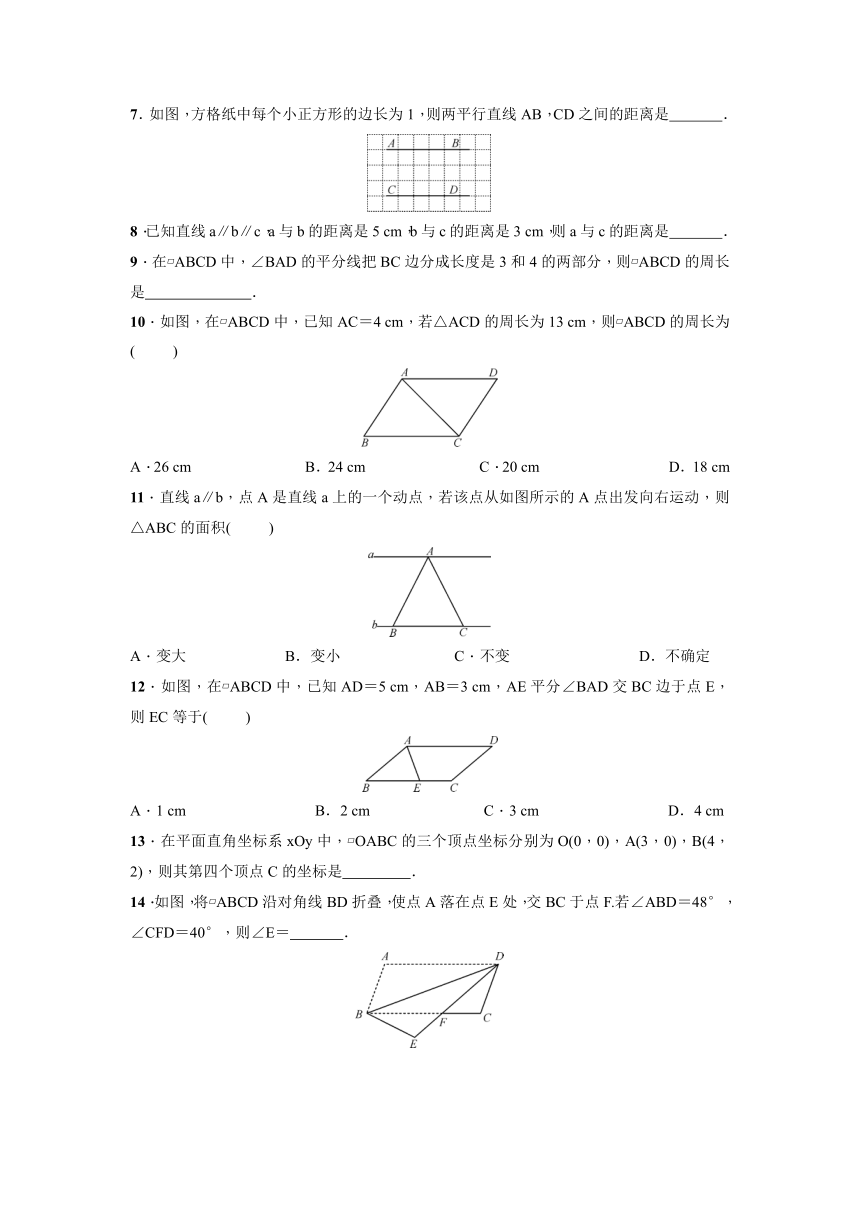
1.如图,在?ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有( )
A.12个 B.9个 C.7个 D.5个
2.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合部分构成一个四边形,这个四边形是 ;理由是 .
3.如图,在?ABCD中,E是AB延长线上的一点,若∠D=120°,则∠1的度数为( )
A.120° B.60° C.45° D.30°
4.在?ABCD中,∠A∶∠B∶∠C∶∠D的值可能是( )
A.2∶5∶2∶5 B.3∶4∶4∶5
C.4∶4∶3∶2 D.2∶3∶5∶6
5.(1)在?ABCD 中,若∠B+∠D=200°,则∠A= ;若∠A∶∠B=5∶4,则∠C= ;
(2)已知?ABCD 的周长为28 cm,若AB∶BC=3∶4,则AB= ,BC= .
6.已知:如图,E是?ABCD的边BC延长线上的一点,且CE=BC.求证:△ABC≌△DCE.
7.如图,方格纸中每个小正方形的边长为1,则两平行直线AB,CD之间的距离是 .
8.已知直线a∥b∥c,a与b的距离是5 cm,b与c的距离是3 cm,则a与c的距离是 .
9.在?ABCD中,∠BAD的平分线把BC边分成长度是3和4的两部分,则?ABCD的周长是 .
10.如图,在?ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则?ABCD的周长为( )
A.26 cm B.24 cm C.20 cm D.18 cm
11.直线a∥b,点A是直线a上的一个动点,若该点从如图所示的A点出发向右运动,则△ABC的面积( )
A.变大 B.变小 C.不变 D.不确定
12.如图,在?ABCD中,已知AD=5 cm,AB=3 cm,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 cm B.2 cm C.3 cm D.4 cm
13.在平面直角坐标系xOy中,?OABC的三个顶点坐标分别为O(0,0),A(3,0),B(4,2),则其第四个顶点C的坐标是 .
14.如图,将?ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E= .
15.如图,点E是?ABCD的边CD的中点,AE,BC的延长线交于点F,CF=3,CE=2,求?ABCD的周长.
16.如图,?ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于点O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AD的长.
第2课时 平行四边形对角线的性质
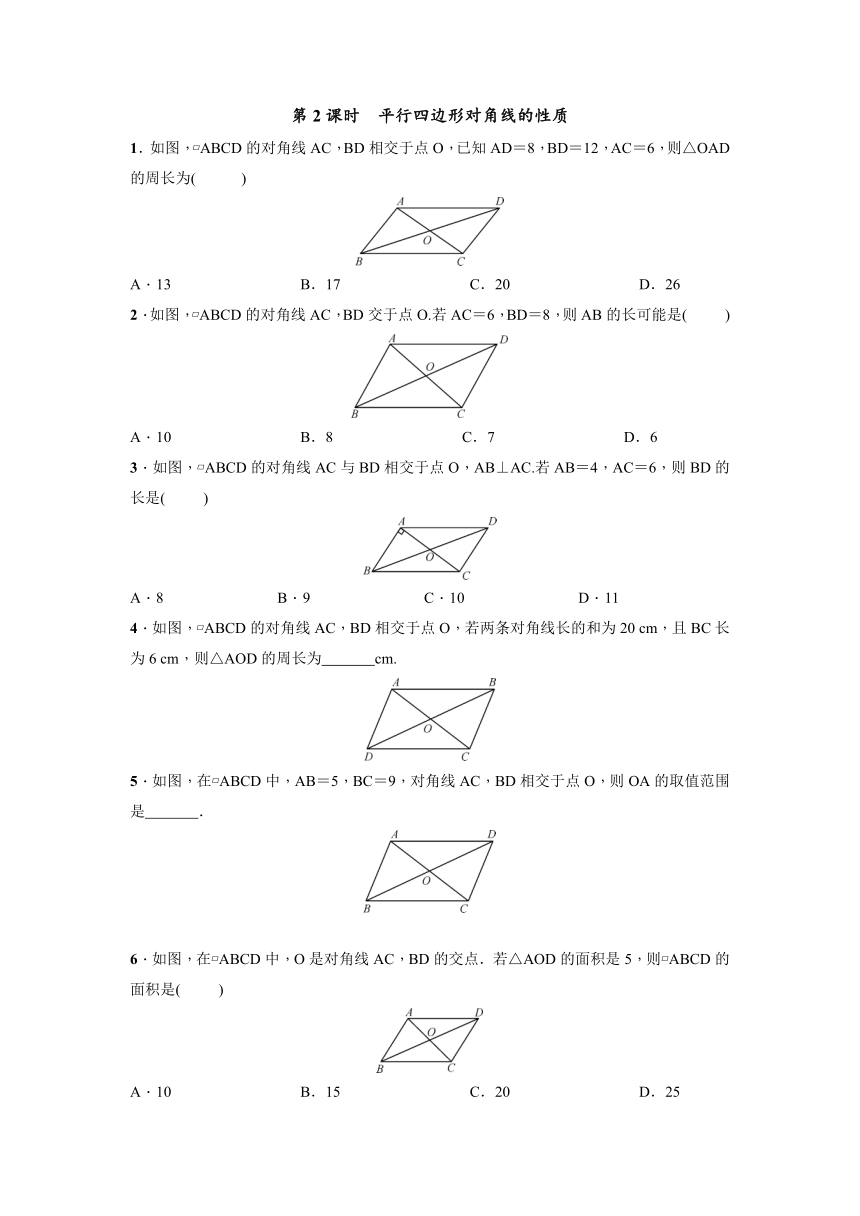
1.如图,?ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OAD的周长为( )
A.13 B.17 C.20 D.26
2.如图,?ABCD的对角线AC,BD交于点O.若AC=6,BD=8,则AB的长可能是( )
A.10 B.8 C.7 D.6
3.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
4.如图,?ABCD的对角线AC,BD相交于点O,若两条对角线长的和为20 cm,且BC长为6 cm,则△AOD的周长为 cm.
5.如图,在?ABCD中,AB=5,BC=9,对角线AC,BD相交于点O,则OA的取值范围是 .
6.如图,在?ABCD中,O是对角线AC,BD的交点.若△AOD的面积是5,则?ABCD的面积是( )
A.10 B.15 C.20 D.25
7.如图,?ABCD的对角线AC的长为10 cm,∠CAB=30°,AB的长为6 cm,则?ABCD的面积为( )
A.60 cm2 B.30 cm2 C.20 cm2 D.16 cm2
8.在?ABCD中,AE⊥BC于点E,若AB=10 cm,BC=15 cm,BE=6 cm,则?ABCD的面积为 .
9.如图,在?ABCD中,对角线AC与BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,则图中全等三角形共有( )
A.7对 B.6对 C.5对 D.4对
10.如图,?ABCD的对角线AC,BD相交于点O,下列结论正确的是( )
A.S?ABCD=4S△AOB B.AC=BD
C.AC⊥BD D.?ABCD是轴对称图形
11.如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线长的和是( )
A.18 B.28 C.36 D.46
12.如图,?ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
13.如图,在?ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若?ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
14.以?ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为(-2,1),则C点坐标为 .
15.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E.若AB=,AC=2,BD=4,则AE的长为 .
16.如图,?ABCD的对角线AC,BD相交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.
37655500(1)求AC的长;
(2)求?ABCD的面积.
17.如图,在?ABCD中,E是AB边上一点,Q是CE的中点,连接BQ并延长交CD于F,连接AF与DE相交于点P.若S△APD=3,S△BQC=5,则图中阴影部分的面积为 .
18.如图1,?ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F,则OE=OF.若将EF向两方延长与平行四边形的两对边的延长线分别相交(图2和图3),OE与OF还相等吗?若相等,请说明你的理由.
参考答案:
18.1.1 平行四边形的性质
第1课时 平行四边形边、角的性质
1.B
2. 平行四边形;理由是两组对边分别平行的四边形是平行四边形.
3.B
4.A
5.(1)在?ABCD 中,若∠B+∠D=200°,则∠A=80°;若∠A∶∠B=5∶4,则∠C=100°;
(2)已知?ABCD 的周长为28 cm,若AB∶BC=3∶4,则AB=6_cm,BC=8_cm.
6.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠B=∠DCE.
在△ABC和△DCE中,
∴△ABC≌△DCE(SAS).
7.3.
8.已知直线a∥b∥c,a与b的距离是5 cm,b与c的距离是3 cm,则a与c的距离是8_cm或2_cm.
9.在?ABCD中,∠BAD的平分线把BC边分成长度是3和4的两部分,则?ABCD的周长是22或20.
10.D
11.C
12.B
13.在平面直角坐标系xOy中,?OABC的三个顶点坐标分别为O(0,0),A(3,0),B(4,2),则其第四个顶点C的坐标是(1,2).
14.112°.
15.解:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠F,∠D=∠ECF.
又∵E是CD的中点,∴ED=EC.
∴△ADE≌△FCE(AAS).
∴AD=CF=3,DE=CE=2.
∴DC=4.
∴?ABCD的周长为2(AD+DC)=14.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB.
∴∠ODF=∠OBE.
在△ODF和△OBE中,
∴△ODF≌△OBE(AAS).∴BO=DO.
(2)∵BD⊥AD,∴∠ADB=90°.
∵∠A=45°,∴∠DBA=∠A=45°.
∴AD=DB.
∵EF⊥AB,∴∠G=∠A=45°.
又∵∠ADB=90°,∴∠DOG=∠G=45°.
∴DO=DG.
∵AB∥CD,EF⊥AB,∴EF⊥CD.∴∠DFG=90°.
∵∠G=45°,∴∠GDF=∠G=45°.
∴DF=FG=1.
∴DG==.
∵BO=DO,
∴DB=2DO=2DG=2.
∴AD=DB=2.
第2课时 平行四边形对角线的性质
1.B
2.D
3.C
4.16cm.
5.2<OA<7.
6.C
7.B
8. 120_cm2.
9.A
10.A
11.C
12.C
13.D
14. (2,-1).
15..
16.解:(1)∵AO∶BO=2∶3,
∴设AO=2x,BO=3x(x>0).
∵AC⊥AB,AB=2,
∴(2x)2+(2)2=(3x)2.
解得x=2.∴AO=4.
∵四边形ABCD是平行四边形,
∴AC=2AO=8.
(2)∵S△ABC=AB·AC=×2×8=8,
∴S?ABCD=2S△ABC=2×8=16.
17.13.
18.解:图2中仍然相等.理由:
∵在?ABCD中,
AB∥CD,OA=OC,
∴∠E=∠F.
在△AOE和△COF中,
∴△AOE≌△COF(AAS).
∴OE=OF.
图3中仍然相等.理由:
∵在?ABCD中,
AD∥BC,OA=OC,
∴∠E=∠F.
在△AOE和△COF中,
∴△AOE≌△COF(AAS).
∴OE=OF.
第1课时 平行四边形边、角的性质
1.如图,在?ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有( )
A.12个 B.9个 C.7个 D.5个
2.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合部分构成一个四边形,这个四边形是 ;理由是 .
3.如图,在?ABCD中,E是AB延长线上的一点,若∠D=120°,则∠1的度数为( )
A.120° B.60° C.45° D.30°
4.在?ABCD中,∠A∶∠B∶∠C∶∠D的值可能是( )
A.2∶5∶2∶5 B.3∶4∶4∶5
C.4∶4∶3∶2 D.2∶3∶5∶6
5.(1)在?ABCD 中,若∠B+∠D=200°,则∠A= ;若∠A∶∠B=5∶4,则∠C= ;
(2)已知?ABCD 的周长为28 cm,若AB∶BC=3∶4,则AB= ,BC= .
6.已知:如图,E是?ABCD的边BC延长线上的一点,且CE=BC.求证:△ABC≌△DCE.
7.如图,方格纸中每个小正方形的边长为1,则两平行直线AB,CD之间的距离是 .
8.已知直线a∥b∥c,a与b的距离是5 cm,b与c的距离是3 cm,则a与c的距离是 .
9.在?ABCD中,∠BAD的平分线把BC边分成长度是3和4的两部分,则?ABCD的周长是 .
10.如图,在?ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则?ABCD的周长为( )
A.26 cm B.24 cm C.20 cm D.18 cm
11.直线a∥b,点A是直线a上的一个动点,若该点从如图所示的A点出发向右运动,则△ABC的面积( )
A.变大 B.变小 C.不变 D.不确定
12.如图,在?ABCD中,已知AD=5 cm,AB=3 cm,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 cm B.2 cm C.3 cm D.4 cm
13.在平面直角坐标系xOy中,?OABC的三个顶点坐标分别为O(0,0),A(3,0),B(4,2),则其第四个顶点C的坐标是 .
14.如图,将?ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E= .
15.如图,点E是?ABCD的边CD的中点,AE,BC的延长线交于点F,CF=3,CE=2,求?ABCD的周长.
16.如图,?ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于点O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AD的长.
第2课时 平行四边形对角线的性质
1.如图,?ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OAD的周长为( )
A.13 B.17 C.20 D.26
2.如图,?ABCD的对角线AC,BD交于点O.若AC=6,BD=8,则AB的长可能是( )
A.10 B.8 C.7 D.6
3.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
4.如图,?ABCD的对角线AC,BD相交于点O,若两条对角线长的和为20 cm,且BC长为6 cm,则△AOD的周长为 cm.
5.如图,在?ABCD中,AB=5,BC=9,对角线AC,BD相交于点O,则OA的取值范围是 .
6.如图,在?ABCD中,O是对角线AC,BD的交点.若△AOD的面积是5,则?ABCD的面积是( )
A.10 B.15 C.20 D.25
7.如图,?ABCD的对角线AC的长为10 cm,∠CAB=30°,AB的长为6 cm,则?ABCD的面积为( )
A.60 cm2 B.30 cm2 C.20 cm2 D.16 cm2
8.在?ABCD中,AE⊥BC于点E,若AB=10 cm,BC=15 cm,BE=6 cm,则?ABCD的面积为 .
9.如图,在?ABCD中,对角线AC与BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,则图中全等三角形共有( )
A.7对 B.6对 C.5对 D.4对
10.如图,?ABCD的对角线AC,BD相交于点O,下列结论正确的是( )
A.S?ABCD=4S△AOB B.AC=BD
C.AC⊥BD D.?ABCD是轴对称图形
11.如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线长的和是( )
A.18 B.28 C.36 D.46
12.如图,?ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3 B.6 C.12 D.24
13.如图,在?ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若?ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
14.以?ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为(-2,1),则C点坐标为 .
15.如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E.若AB=,AC=2,BD=4,则AE的长为 .
16.如图,?ABCD的对角线AC,BD相交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.
37655500(1)求AC的长;
(2)求?ABCD的面积.
17.如图,在?ABCD中,E是AB边上一点,Q是CE的中点,连接BQ并延长交CD于F,连接AF与DE相交于点P.若S△APD=3,S△BQC=5,则图中阴影部分的面积为 .
18.如图1,?ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F,则OE=OF.若将EF向两方延长与平行四边形的两对边的延长线分别相交(图2和图3),OE与OF还相等吗?若相等,请说明你的理由.
参考答案:
18.1.1 平行四边形的性质
第1课时 平行四边形边、角的性质
1.B
2. 平行四边形;理由是两组对边分别平行的四边形是平行四边形.
3.B
4.A
5.(1)在?ABCD 中,若∠B+∠D=200°,则∠A=80°;若∠A∶∠B=5∶4,则∠C=100°;
(2)已知?ABCD 的周长为28 cm,若AB∶BC=3∶4,则AB=6_cm,BC=8_cm.
6.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠B=∠DCE.
在△ABC和△DCE中,
∴△ABC≌△DCE(SAS).
7.3.
8.已知直线a∥b∥c,a与b的距离是5 cm,b与c的距离是3 cm,则a与c的距离是8_cm或2_cm.
9.在?ABCD中,∠BAD的平分线把BC边分成长度是3和4的两部分,则?ABCD的周长是22或20.
10.D
11.C
12.B
13.在平面直角坐标系xOy中,?OABC的三个顶点坐标分别为O(0,0),A(3,0),B(4,2),则其第四个顶点C的坐标是(1,2).
14.112°.
15.解:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠F,∠D=∠ECF.
又∵E是CD的中点,∴ED=EC.
∴△ADE≌△FCE(AAS).
∴AD=CF=3,DE=CE=2.
∴DC=4.
∴?ABCD的周长为2(AD+DC)=14.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB.
∴∠ODF=∠OBE.
在△ODF和△OBE中,
∴△ODF≌△OBE(AAS).∴BO=DO.
(2)∵BD⊥AD,∴∠ADB=90°.
∵∠A=45°,∴∠DBA=∠A=45°.
∴AD=DB.
∵EF⊥AB,∴∠G=∠A=45°.
又∵∠ADB=90°,∴∠DOG=∠G=45°.
∴DO=DG.
∵AB∥CD,EF⊥AB,∴EF⊥CD.∴∠DFG=90°.
∵∠G=45°,∴∠GDF=∠G=45°.
∴DF=FG=1.
∴DG==.
∵BO=DO,
∴DB=2DO=2DG=2.
∴AD=DB=2.
第2课时 平行四边形对角线的性质
1.B
2.D
3.C
4.16cm.
5.2<OA<7.
6.C
7.B
8. 120_cm2.
9.A
10.A
11.C
12.C
13.D
14. (2,-1).
15..
16.解:(1)∵AO∶BO=2∶3,
∴设AO=2x,BO=3x(x>0).
∵AC⊥AB,AB=2,
∴(2x)2+(2)2=(3x)2.
解得x=2.∴AO=4.
∵四边形ABCD是平行四边形,
∴AC=2AO=8.
(2)∵S△ABC=AB·AC=×2×8=8,
∴S?ABCD=2S△ABC=2×8=16.
17.13.
18.解:图2中仍然相等.理由:
∵在?ABCD中,
AB∥CD,OA=OC,
∴∠E=∠F.
在△AOE和△COF中,
∴△AOE≌△COF(AAS).
∴OE=OF.
图3中仍然相等.理由:
∵在?ABCD中,
AD∥BC,OA=OC,
∴∠E=∠F.
在△AOE和△COF中,
∴△AOE≌△COF(AAS).
∴OE=OF.
