人教版数学八年级下册:第十八章 平行四边形 章末练习(word版附答案)
文档属性
| 名称 | 人教版数学八年级下册:第十八章 平行四边形 章末练习(word版附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 110.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 07:24:59 | ||
图片预览

文档简介
平行四边形 章末复习
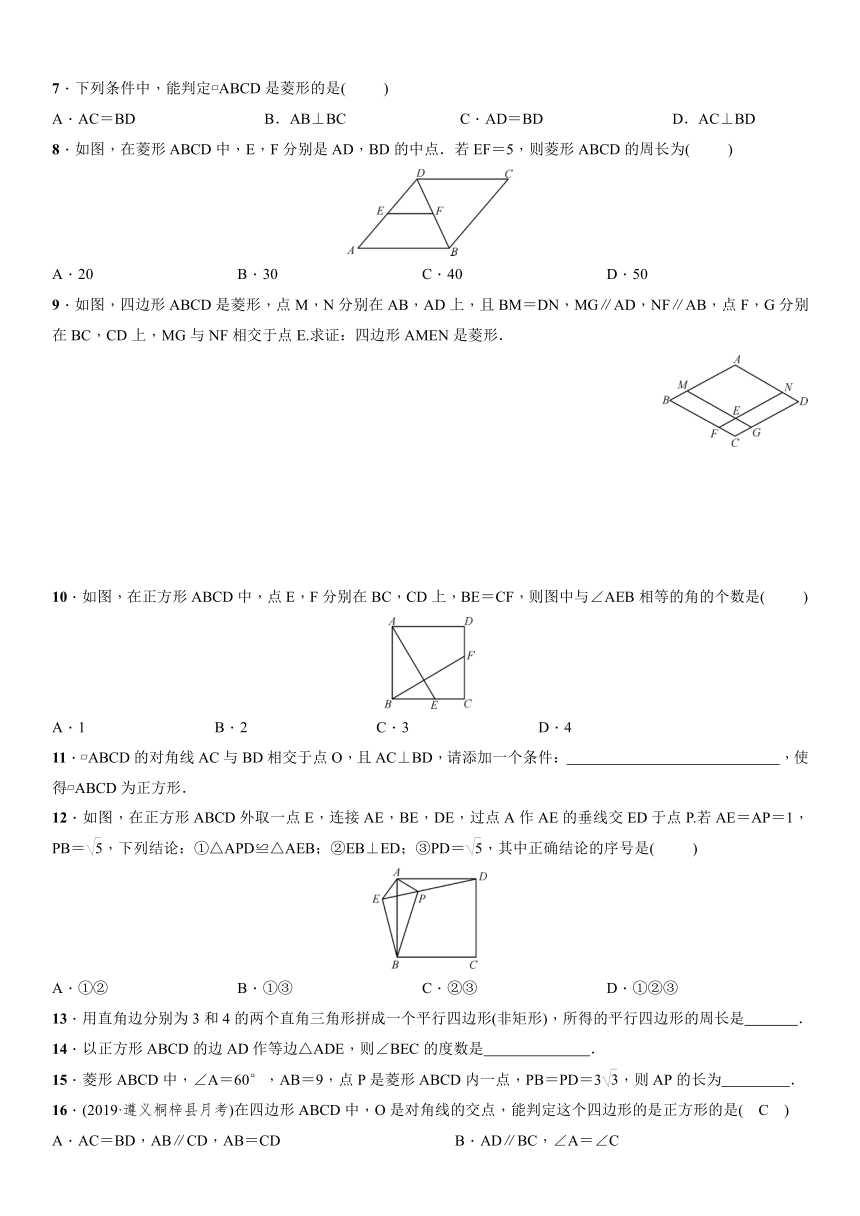
1.如图,?ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
2.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为( )
A.8 B.10 C.12 D.14
3.如图,在?ABCD中,AE=CF,M,N分别是BE,DF的中点,求证:四边形MFNE是平行四边形.
4.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°.若AB=5,BC=8,则EF的长为 .
5.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=( )
A.5 B.4 C.3.5 D.3
6.如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形.
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
7.下列条件中,能判定?ABCD是菱形的是( )
A.AC=BD B.AB⊥BC C.AD=BD D.AC⊥BD
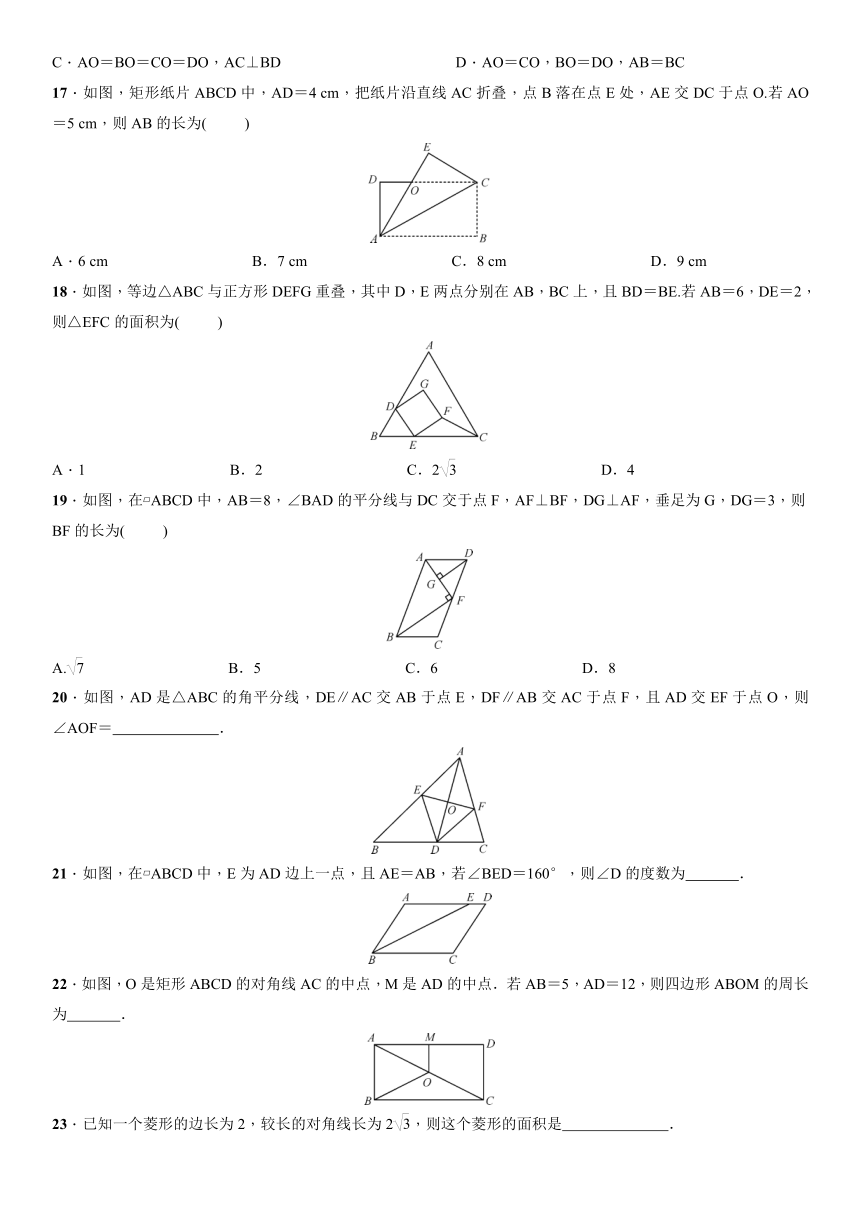
8.如图,在菱形ABCD中,E,F分别是AD,BD的中点.若EF=5,则菱形ABCD的周长为( )
A.20 B.30 C.40 D.50
9.如图,四边形ABCD是菱形,点M,N分别在AB,AD上,且BM=DN,MG∥AD,NF∥AB,点F,G分别在BC,CD上,MG与NF相交于点E.求证:四边形AMEN是菱形.
10.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
11.?ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得?ABCD为正方形.
12.如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交ED于点P.若AE=AP=1,PB=,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=,其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
13.用直角边分别为3和4的两个直角三角形拼成一个平行四边形(非矩形),所得的平行四边形的周长是 .
14.以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是 .
15.菱形ABCD中,∠A=60°,AB=9,点P是菱形ABCD内一点,PB=PD=3,则AP的长为 .
16.(2019·遵义桐梓县月考)在四边形ABCD中,O是对角线的交点,能判定这个四边形的是正方形的是( C )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC
17.如图,矩形纸片ABCD中,AD=4 cm,把纸片沿直线AC折叠,点B落在点E处,AE交DC于点O.若AO=5 cm,则AB的长为( )
A.6 cm B.7 cm C.8 cm D.9 cm
18.如图,等边△ABC与正方形DEFG重叠,其中D,E两点分别在AB,BC上,且BD=BE.若AB=6,DE=2,则△EFC的面积为( )
A.1 B.2 C.2 D.4
19.如图,在?ABCD中,AB=8,∠BAD的平分线与DC交于点F,AF⊥BF,DG⊥AF,垂足为G,DG=3,则BF的长为( )
A. B.5 C.6 D.8
20.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,且AD交EF于点O,则∠AOF= .
21.如图,在?ABCD中,E为AD边上一点,且AE=AB,若∠BED=160°,则∠D的度数为 .
22.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .
23.已知一个菱形的边长为2,较长的对角线长为2,则这个菱形的面积是 .
24.如图,ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F,G.求证:BF-DG=FG.
25.△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连接BE.
(1)如图1所示,当点D在线段BC上时,探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图2所示,当点D在BC的延长线上运动到什么位置时,四边形BCGE是菱形?并说明理由.
参考答案:
1.B
2.B
3.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
又∵AE=CF,∴AD-AE=BC-CF,即DE=BF.
∴四边形BEDF是平行四边形.
∴BE∥DF,BE=DF.
∵M,N分别是BE,DF的中点,
∴EM=BE=DF=NF.
∴四边形MFNE是平行四边形.
4..
5.B
6.解:(1)证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形.
∵∠AOB=∠OAD+∠ADO=2∠OAD,
∴∠OAD=∠ADO.
∴AO=DO.∴AC=BD.
∴四边形ABCD是矩形.
(2)∵四边形ABCD是矩形,
∴AB∥CD,∠BAD=90°.∴∠ABO=∠ODC.
∵∠AOB∶∠ODC=4∶3,
∴∠AOB∶∠ABO=4∶3.
∴∠BAO∶∠AOB∶∠ABO=3∶4∶3.
∴∠ABO=180°×=54°.
∴∠ADO=90°-∠ABO=36°.
7.D
8.C
9.证明:∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形.
∵四边形ABCD是菱形,
∴AB=AD.
∵BM=DN,
∴AB-BM=AD-DN,即AM=AN.
∴四边形AMEN是菱形.
10.C
11.答案不唯一,如:AC=BD
12.A
13. 16或18.
14. 30°或150°.
15. 3或6.
16.C
17.C
18.B
19.C
20. 90°.
21.40°.
22.20.
23.2.
24.证明:∵四边形ABCD是正方形,
∴AB=AD,∠DAB=90°.
∵BF⊥AE,DG⊥AE,
∴∠AFB=∠AGD=∠ADG+∠DAG=90°.
∵∠DAG+∠BAF=90°,
∴∠ADG=∠BAF.
在△BAF和△ADG中,
∴△BAF≌△ADG(AAS).
∴BF=AG,AF=DG.
∵AG=AF+FG,
∴BF=AG=DG+FG.
∴BF-DG=FG.
25.解:(1)四边形BCGE是平行四边形.
理由:∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵∠EAB=∠EAD-∠BAD,
∠DAC=∠BAC-∠BAD,
∴∠EAB=∠DAC.
∴△AEB≌△ADC(SAS).
∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,∴∠ABE=∠BAC.
∴EB∥GC.
又∵EG∥BC,∴四边形BCGE是平行四边形.
(2)当CD=CB(∠CAD=30°或∠BAD=90°或∠ADC=30°)时,四边形BCGE是菱形.
理由:由(1)得△AEB≌△ADC,
∴BE=CD,∠ACD=∠ABE=120°.
又∵∠ABC=∠ACB=∠DCG=60°,
∴∠EBC=∠ABE-∠ABC=120°-60°=60°=∠DCG.
∴BE∥CG.
又∵EG∥BC,∴四边形BCGE是平行四边形.
又∵CD=CB,∴BE=CD.
∴BE=BC,∴四边形BCGE是菱形.
1.如图,?ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
2.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为( )
A.8 B.10 C.12 D.14
3.如图,在?ABCD中,AE=CF,M,N分别是BE,DF的中点,求证:四边形MFNE是平行四边形.
4.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°.若AB=5,BC=8,则EF的长为 .
5.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=( )
A.5 B.4 C.3.5 D.3
6.如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形.
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
7.下列条件中,能判定?ABCD是菱形的是( )
A.AC=BD B.AB⊥BC C.AD=BD D.AC⊥BD
8.如图,在菱形ABCD中,E,F分别是AD,BD的中点.若EF=5,则菱形ABCD的周长为( )
A.20 B.30 C.40 D.50
9.如图,四边形ABCD是菱形,点M,N分别在AB,AD上,且BM=DN,MG∥AD,NF∥AB,点F,G分别在BC,CD上,MG与NF相交于点E.求证:四边形AMEN是菱形.
10.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
11.?ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得?ABCD为正方形.
12.如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交ED于点P.若AE=AP=1,PB=,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=,其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
13.用直角边分别为3和4的两个直角三角形拼成一个平行四边形(非矩形),所得的平行四边形的周长是 .
14.以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是 .
15.菱形ABCD中,∠A=60°,AB=9,点P是菱形ABCD内一点,PB=PD=3,则AP的长为 .
16.(2019·遵义桐梓县月考)在四边形ABCD中,O是对角线的交点,能判定这个四边形的是正方形的是( C )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC
17.如图,矩形纸片ABCD中,AD=4 cm,把纸片沿直线AC折叠,点B落在点E处,AE交DC于点O.若AO=5 cm,则AB的长为( )
A.6 cm B.7 cm C.8 cm D.9 cm
18.如图,等边△ABC与正方形DEFG重叠,其中D,E两点分别在AB,BC上,且BD=BE.若AB=6,DE=2,则△EFC的面积为( )
A.1 B.2 C.2 D.4
19.如图,在?ABCD中,AB=8,∠BAD的平分线与DC交于点F,AF⊥BF,DG⊥AF,垂足为G,DG=3,则BF的长为( )
A. B.5 C.6 D.8
20.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,且AD交EF于点O,则∠AOF= .
21.如图,在?ABCD中,E为AD边上一点,且AE=AB,若∠BED=160°,则∠D的度数为 .
22.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .
23.已知一个菱形的边长为2,较长的对角线长为2,则这个菱形的面积是 .
24.如图,ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F,G.求证:BF-DG=FG.
25.△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连接BE.
(1)如图1所示,当点D在线段BC上时,探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图2所示,当点D在BC的延长线上运动到什么位置时,四边形BCGE是菱形?并说明理由.
参考答案:
1.B
2.B
3.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
又∵AE=CF,∴AD-AE=BC-CF,即DE=BF.
∴四边形BEDF是平行四边形.
∴BE∥DF,BE=DF.
∵M,N分别是BE,DF的中点,
∴EM=BE=DF=NF.
∴四边形MFNE是平行四边形.
4..
5.B
6.解:(1)证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形.
∵∠AOB=∠OAD+∠ADO=2∠OAD,
∴∠OAD=∠ADO.
∴AO=DO.∴AC=BD.
∴四边形ABCD是矩形.
(2)∵四边形ABCD是矩形,
∴AB∥CD,∠BAD=90°.∴∠ABO=∠ODC.
∵∠AOB∶∠ODC=4∶3,
∴∠AOB∶∠ABO=4∶3.
∴∠BAO∶∠AOB∶∠ABO=3∶4∶3.
∴∠ABO=180°×=54°.
∴∠ADO=90°-∠ABO=36°.
7.D
8.C
9.证明:∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形.
∵四边形ABCD是菱形,
∴AB=AD.
∵BM=DN,
∴AB-BM=AD-DN,即AM=AN.
∴四边形AMEN是菱形.
10.C
11.答案不唯一,如:AC=BD
12.A
13. 16或18.
14. 30°或150°.
15. 3或6.
16.C
17.C
18.B
19.C
20. 90°.
21.40°.
22.20.
23.2.
24.证明:∵四边形ABCD是正方形,
∴AB=AD,∠DAB=90°.
∵BF⊥AE,DG⊥AE,
∴∠AFB=∠AGD=∠ADG+∠DAG=90°.
∵∠DAG+∠BAF=90°,
∴∠ADG=∠BAF.
在△BAF和△ADG中,
∴△BAF≌△ADG(AAS).
∴BF=AG,AF=DG.
∵AG=AF+FG,
∴BF=AG=DG+FG.
∴BF-DG=FG.
25.解:(1)四边形BCGE是平行四边形.
理由:∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵∠EAB=∠EAD-∠BAD,
∠DAC=∠BAC-∠BAD,
∴∠EAB=∠DAC.
∴△AEB≌△ADC(SAS).
∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,∴∠ABE=∠BAC.
∴EB∥GC.
又∵EG∥BC,∴四边形BCGE是平行四边形.
(2)当CD=CB(∠CAD=30°或∠BAD=90°或∠ADC=30°)时,四边形BCGE是菱形.
理由:由(1)得△AEB≌△ADC,
∴BE=CD,∠ACD=∠ABE=120°.
又∵∠ABC=∠ACB=∠DCG=60°,
∴∠EBC=∠ABE-∠ABC=120°-60°=60°=∠DCG.
∴BE∥CG.
又∵EG∥BC,∴四边形BCGE是平行四边形.
又∵CD=CB,∴BE=CD.
∴BE=BC,∴四边形BCGE是菱形.
