2020—2021学年八年级数学北师大版下册同步课件 第2章6 一元一次不等式组 第1课时(27张PPT)
文档属性
| 名称 | 2020—2021学年八年级数学北师大版下册同步课件 第2章6 一元一次不等式组 第1课时(27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 231.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 08:29:49 | ||
图片预览







文档简介
(共27张PPT)
第二章
一元一次不等式与一元一次不等式组
6
一元一次不等式组
第1课时
一元一次不等式组(一)
目录
02
课堂讲练
01
名师导学
03
分层训练
名师导学
A.
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个__________________.
1.
下列不等式组是一元一次不等式组的是(
)
A.
x>2,
B.
x+1>0,
x<-3
y-2<0
C.
3x-2>0,
D.
3x-2>0,
(x-2)(x+3)>0
x+1<
一元一次不等式组
A
B.
一元一次不等式组中各个不等式的解集的_________部分,叫做这个一元一次不等式组的解集.
求不等式组解集的过程叫做解不等式组.
公共
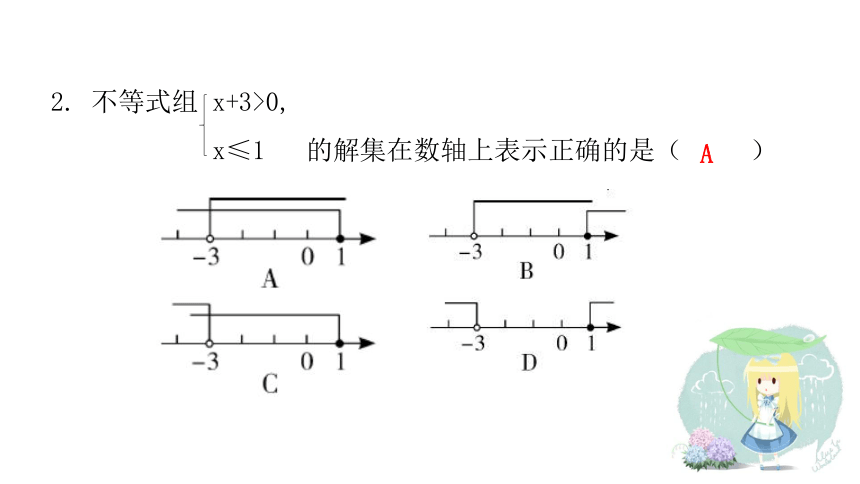
2.
不等式组
x+3>0,
x≤1
的解集在数轴上表示正确的是(
)
A
课堂讲练
【例1】判断下列各不等式组是否为一元一次不等式组.
(1)
x+2<3x,
(2)
x2+1>2x,
y>1;
x<1;
(3)
x+1>2x,
(4)
x-1>0,
x<-1;
x+1<0,
(5)
2x-8≤7-x,
x-3>2x-1;
7-x<5.
典型例题
知识点1:
一元一次不等式组的概念
解:(3)
(4)
(5)
是一元一次不等式组.
思路点拨:根据一元一次不等式组的定义判断.
1.
下列不等式组中,一元一次不等式组的个数有(
)
①
x>-2,
②
x>0,
③
x>x2+1,
x<3;
x+2>0;
x2+2x>4;
④
x+3x>0,⑤
x+1>0,
x<-7;
y-1<x.
A.
2个
B.
3个
C.
4个
D.
5个
举一反三
B
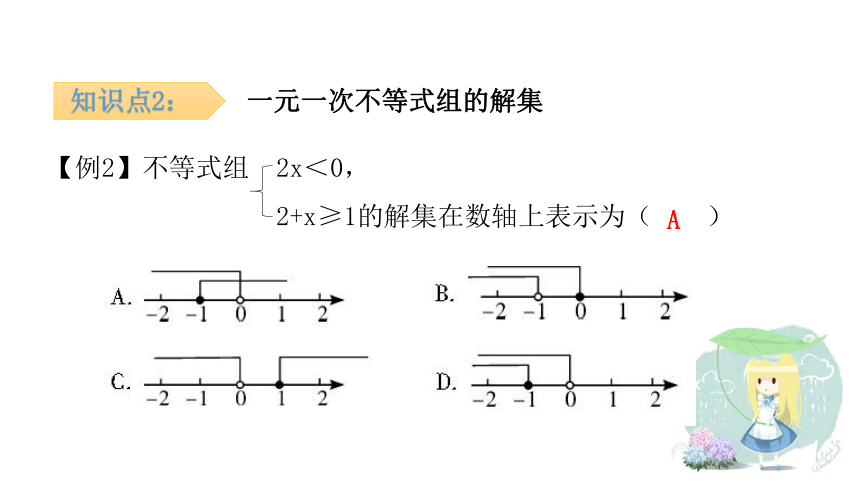
【例2】不等式组
2x<0,
2+x≥1的解集在数轴上表示为(
)
知识点2:
一元一次不等式组的解集
A
2.
如图2-6-1,解集是数轴上表示的不等式组为(
)
图2-6-1
A.
x-2≥0,
B.
x+2≥0,
3-x>0
x-3>0
C.
x-2≥0,
D.
2-x≥0,
3+x>0
3-x>0
A
【例3】关于x的不等式组
x-m<0,
3x-1>2(x-1)
无解,
那么m的取值范围是(
)
A.
m≤-1
B.
m<-1
C.
-1<m≤0
D.
-1≤m<0
思路点拨:根据“同小取小、同大取大、大大小小无解、大小小大取中间”,即可得出答案.
A
3.
若不等式组
1+x>a,
2x-4<0
有解,则a的取值范围是(
)
A.
a≤3
B.
a<3
C.
a<2
D.
a≤2
B
分层训练
【A组】
1.
下列不是一元一次不等式组的是(
)
A.
y<-
,
B.
3x-5>0,
y>5
4x+2<0
C.
a-1<0,
D.
x-5>0,
b+2>0
x+2<0,
4x+8<9
C
2.
下列不等式组:①
5x>-2,
②
x>0,
15x<3;
x-3>4;
③
x2+5④
x+3>0,
⑤
x2+1>0,
x2+2>4;
x<25;
y-18<0,
其中一元一次不等式组有(
)
A.
2个
B.
3个
C.
4个
D.
5个
B
3.
不等式组
2x-1≥1,
x-2<0
的解集在数轴上表示为(
)
C
4.
在平面直角坐标系中,点P(6-2x,x-5)在第三象限,则x的取值范围是(
)
A.
x>5
B.
3<x<5
C.
x<3
D.
-3<x<5
B
5.
写出下列数轴上所表示的不等式组的解集:
(1)
_____________;
(2)
____________.
-2≤x<3
x>2
6.
不等式组的解集在数轴上表示如图2-6-2所示,则该不等式组是(
)
图2-6-2
A.
x-1<3
B.
x-1<3
x+1<3
x+1>3
C.
x-1>3
D.
x-1>3
x+1>3
x+1<3
B
7.
不等式组
2x+1≥-3,
x<1
的解集在数轴上表示正确的是(
)
B
【B组】
8.
已知关于x的不等式
x-a≥0,
5-2x>1只有四个整数解,则实数a的取值范是_______________.
9.
关于x的不等式组
x-a≤0,
2x+3a>0
的解集中至少有5个整数解,则正数a的最小值是(
)
A.
3
B.
2
C.
1
D.
23
-3<a≤-2
B
10.
已知关于x的不等式组
3x-1<4(x-1),
x<m
无解,则m的取值范围是(
)
A.
m≤3
B.
m>3
C.
m<3
D.
m≥3
A
【C组】
11.
已知关于x,y的方程组
x-2y=m,①
2x+3y=2m+4②
的解满足不等式组
3x+y≤0,
x+5y>0.
求满足条件的m的整数值.
解:①×2,得2x-4y=2m.③
②-③,得y=
.
把y=
代入①,得x=m+
.
把x=m+
,y=
代入不等式组
3x+y≤0,
x+5y>0,
得
3m+4≤0,
m+4>0.
解该不等式组,得-4<m≤-
.
则m的整数值为-3,-2.
4
___
7
4
___
7
8
___
7
8
___
7
4
___
3
4
___
7
12.
若一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
例如:方程2x-6=0的解为x=3,不等式组
x-1>0,
x<4
的解集为1<x<4.
因为1<3<4,所以称方程2x-6=0为不等式组
x-1>0,
x<4
的关联方程.
(1)在方程
①3x-2=0,②
x+1=0,③x-(3x+1)=-5中,不等式组
2x+3>3x-1,
-4x-3<x+2
的关联方程是_____;(填序号)
(2)若方程2x-1=x+2,x+3=2(x+
)都是关于x的
不等式组
x<2x-m,
x-2≤m
的关联方程,
求m的取值范围.
①③
解:(2)由
x<2x-m,
x-2≤m,
解得m<x≤m+2.
∵方程2x-1=x+2的解为x=3,
方程x+3=2(x+
)的解为x=2,
∴m的取值范围为1≤m<2.
1
___
2
谢
谢
第二章
一元一次不等式与一元一次不等式组
6
一元一次不等式组
第1课时
一元一次不等式组(一)
目录
02
课堂讲练
01
名师导学
03
分层训练
名师导学
A.
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个__________________.
1.
下列不等式组是一元一次不等式组的是(
)
A.
x>2,
B.
x+1>0,
x<-3
y-2<0
C.
3x-2>0,
D.
3x-2>0,
(x-2)(x+3)>0
x+1<
一元一次不等式组
A
B.
一元一次不等式组中各个不等式的解集的_________部分,叫做这个一元一次不等式组的解集.
求不等式组解集的过程叫做解不等式组.
公共
2.
不等式组
x+3>0,
x≤1
的解集在数轴上表示正确的是(
)
A
课堂讲练
【例1】判断下列各不等式组是否为一元一次不等式组.
(1)
x+2<3x,
(2)
x2+1>2x,
y>1;
x<1;
(3)
x+1>2x,
(4)
x-1>0,
x<-1;
x+1<0,
(5)
2x-8≤7-x,
x-3>2x-1;
7-x<5.
典型例题
知识点1:
一元一次不等式组的概念
解:(3)
(4)
(5)
是一元一次不等式组.
思路点拨:根据一元一次不等式组的定义判断.
1.
下列不等式组中,一元一次不等式组的个数有(
)
①
x>-2,
②
x>0,
③
x>x2+1,
x<3;
x+2>0;
x2+2x>4;
④
x+3x>0,⑤
x+1>0,
x<-7;
y-1<x.
A.
2个
B.
3个
C.
4个
D.
5个
举一反三
B
【例2】不等式组
2x<0,
2+x≥1的解集在数轴上表示为(
)
知识点2:
一元一次不等式组的解集
A
2.
如图2-6-1,解集是数轴上表示的不等式组为(
)
图2-6-1
A.
x-2≥0,
B.
x+2≥0,
3-x>0
x-3>0
C.
x-2≥0,
D.
2-x≥0,
3+x>0
3-x>0
A
【例3】关于x的不等式组
x-m<0,
3x-1>2(x-1)
无解,
那么m的取值范围是(
)
A.
m≤-1
B.
m<-1
C.
-1<m≤0
D.
-1≤m<0
思路点拨:根据“同小取小、同大取大、大大小小无解、大小小大取中间”,即可得出答案.
A
3.
若不等式组
1+x>a,
2x-4<0
有解,则a的取值范围是(
)
A.
a≤3
B.
a<3
C.
a<2
D.
a≤2
B
分层训练
【A组】
1.
下列不是一元一次不等式组的是(
)
A.
y<-
,
B.
3x-5>0,
y>5
4x+2<0
C.
a-1<0,
D.
x-5>0,
b+2>0
x+2<0,
4x+8<9
C
2.
下列不等式组:①
5x>-2,
②
x>0,
15x<3;
x-3>4;
③
x2+5
x+3>0,
⑤
x2+1>0,
x2+2>4;
x<25;
y-18<0,
其中一元一次不等式组有(
)
A.
2个
B.
3个
C.
4个
D.
5个
B
3.
不等式组
2x-1≥1,
x-2<0
的解集在数轴上表示为(
)
C
4.
在平面直角坐标系中,点P(6-2x,x-5)在第三象限,则x的取值范围是(
)
A.
x>5
B.
3<x<5
C.
x<3
D.
-3<x<5
B
5.
写出下列数轴上所表示的不等式组的解集:
(1)
_____________;
(2)
____________.
-2≤x<3
x>2
6.
不等式组的解集在数轴上表示如图2-6-2所示,则该不等式组是(
)
图2-6-2
A.
x-1<3
B.
x-1<3
x+1<3
x+1>3
C.
x-1>3
D.
x-1>3
x+1>3
x+1<3
B
7.
不等式组
2x+1≥-3,
x<1
的解集在数轴上表示正确的是(
)
B
【B组】
8.
已知关于x的不等式
x-a≥0,
5-2x>1只有四个整数解,则实数a的取值范是_______________.
9.
关于x的不等式组
x-a≤0,
2x+3a>0
的解集中至少有5个整数解,则正数a的最小值是(
)
A.
3
B.
2
C.
1
D.
23
-3<a≤-2
B
10.
已知关于x的不等式组
3x-1<4(x-1),
x<m
无解,则m的取值范围是(
)
A.
m≤3
B.
m>3
C.
m<3
D.
m≥3
A
【C组】
11.
已知关于x,y的方程组
x-2y=m,①
2x+3y=2m+4②
的解满足不等式组
3x+y≤0,
x+5y>0.
求满足条件的m的整数值.
解:①×2,得2x-4y=2m.③
②-③,得y=
.
把y=
代入①,得x=m+
.
把x=m+
,y=
代入不等式组
3x+y≤0,
x+5y>0,
得
3m+4≤0,
m+4>0.
解该不等式组,得-4<m≤-
.
则m的整数值为-3,-2.
4
___
7
4
___
7
8
___
7
8
___
7
4
___
3
4
___
7
12.
若一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
例如:方程2x-6=0的解为x=3,不等式组
x-1>0,
x<4
的解集为1<x<4.
因为1<3<4,所以称方程2x-6=0为不等式组
x-1>0,
x<4
的关联方程.
(1)在方程
①3x-2=0,②
x+1=0,③x-(3x+1)=-5中,不等式组
2x+3>3x-1,
-4x-3<x+2
的关联方程是_____;(填序号)
(2)若方程2x-1=x+2,x+3=2(x+
)都是关于x的
不等式组
x<2x-m,
x-2≤m
的关联方程,
求m的取值范围.
①③
解:(2)由
x<2x-m,
x-2≤m,
解得m<x≤m+2.
∵方程2x-1=x+2的解为x=3,
方程x+3=2(x+
)的解为x=2,
∴m的取值范围为1≤m<2.
1
___
2
谢
谢
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
