2020-2021学年八年级数学人教版 下册 17.1 用勾股定理求最短路径课件(23张)
文档属性
| 名称 | 2020-2021学年八年级数学人教版 下册 17.1 用勾股定理求最短路径课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 836.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
勾股定理的应用之
求解几何体的最短路线长
B
A
蚂蚁怎么走最近?
例1
如图
在一个底面周长为20cm,高AA′为4cm的圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A
处爬向B处,你们想一想,蚂蚁怎么走最近?
问题情境
A
′
应有公,字财有,公元一千九百三十三年农历五月二十一生,檀林河东罗家冲人氏。于世不久,父丧母亡。家居深山,交通闭塞,徒存四壁,苦不堪言,少有田亩,衣食两难。有兄二人,相继出外谋生;公及弟妹,时龄尚幼,不谙世事,幸叔收养,方有立锥丸地,借以喘息栖身。年稍长,学耕耘,事稼穑,吃苦耐劳,得以早熟,学农活一学即会,长浑身干事气力。公虽无缘学堂,然敏学善思,苦难心悟,茅塞顿开,以精明聪敏为众所闻。是时,社会黑暗,世道无公,虽勤爬苦做、精打细算,仍忍受饥寒、难以为继。每遇春荒,不知饱饭何在;历载彻寒,未得棉衣裹身。所尝之苦,每思之,潸然泪下矣;常忆念,概莫能及哉! 然沧海桑田,星移斗转;世事更迭,其为必然。刘邓大军,挺进大别,战略反攻,序幕拉开。高山铺一役,威慑敌胆,史之所书,甚为壮怀。及至一千九百四十九年,蕲阳民众得见天日,檀林深山拥揽光明。公激情昂奋,一腔赤诚,投身新政。劳作之余,习练文化;公务之中,宣讲政策。浑身之正气,满脑之机灵,始得基层组织赏识,并于一千九百六十四年为党之一员。娶妻孙氏,亦为中共纳新。公任小队保管,饥荒连连,秋毫无犯;履会计岗位,账清目明,分厘不贪;担队长之职,身先士卒,农活拚干。红旗飘飘,尽显党员本色;忠心耿耿,常持赤子情怀。 公所事小队之公务,甚得组织褒奖,遂委以大队财经队长、村主任之职至殁年。公之于公兮,可谓披胆沥胆,催耕催种、兴修水利、抗洪救灾、急难险重,无一不冲锋在前;公之于民兮,可谓倾其所能,邻里纠纷、儿婚女嫁、稚童辍学、扶困助弱,无一不情至力竭。时至今夕,人常念道,修赤东大堤,时值腊月,严寒刺骨,公往返百余公里,徒步来回。只因里程遥偏,无宿营之处,为不违工期,遂河床挖坑、权当床铺,扁担垫身、且作床单,蓑衣覆体、是为棉被。朔风起,霜花降,焉能入睡?夜露寒,冰凝背,何以寝安?又年岁中,暴雨如注,山洪突发,河水暴涨,抗旱机泵,卷入洪流,雨水洗刷,深陷泥潭。公无视湍流之急,冒雨投河,众人感佩,悉数相帮,汗雨淋身,腾挪许久,方遂愿淘出。于公如斯,于民亦然。不乏村民难之受帮、困之受济者,口口相传,嘱晚辈、告儿孙,记公之恩德。此番情景,孰可忘怀? 公虽家境贫寒,但强而不怠,白手起家,兴室创业。常叨念古训:一粥一饭、当思来处不易,半丝半缕、恒念物力维艰。公既念之,亦践行之,严苛以求已,宽厚始待人。时年,三子女继出,家仅瓦屋两间,尤显拥蹇,添缮居室,迫在眉尖。环顾四周,窥视家底,既乏料乏粮,亦无钱无帮,境之所困,未曾吁叹,迎难而上,决然速行。乏料,遂起早贪黑,房前屋后,就地取材;乏粮,则节餐缩食,饥餐饿顿,肚中省粮;无钱无帮,即少请帮工,压减开支,片刻不歇,自行张罗。时约一周,瓦屋两间,遂以垒成。子女年幼,幸有避风挡雨之所;贤妻梦圆,方奠安居乐业之基。责任制后,公值盛年,公干之余,更是披星戴月,劲足冲天,忙碌中不知倦怠。或耕种收获、或上山打柴,或出外卖炭、或与人帮工;即便年卅,或逢阴雨,亦田间地头、山岭沟壑,忙若常态,未曾清闲。抵年末,盘收成,信心满,欣慰露,总胜乡邻几分。公足矣! 呜呼!天有不测风云,地有无端变故,人岂能避祸灾?公元一千九百九十年农历十月二十二日,公寝矣,时值壮年!檀河含悲,泗流垂首,妻儿恸哭,山乡哀号。后有人感公盛年早逝、业绩昭昭,作挽联缅怀,联曰: 天孰有道,可怜幼出寒门含辛茹苦拚事业 地岂瞒情,无愧心连集体沥胆披肝报家园 公外襄田垄,内重家道,严于教子,以身示范,邻里景仰。公时在世,节衣缩食,供孩上学,豁达乐观,涵养家风,深得族人传颂,亦得子女传承。公之两女,均受家风熏陶,品行善良,持家守道,掌衬夫家,上孝下亲,左邻右舍,堪念其范;公之一子,更得公之真传,义薄云天,高朋满座,勤奋敬业,能力过人,赢得侪辈拥戴,深为组织器重。公之孙子女,天资聪慧,术有专攻,学业有成,皆取硕士头衔,一供职于央企要位,一奉薪于鄂省机关。人常言:在世播恩爱,积德荫子孙。公之所为,应此渊源,公寝亦安矣! 噫吁!公之一生,乐善好施,帮人于急切之时;公之此世,正义凛然,挺身于危重之处。世之促,泽被子孙,香火燎原;行之难,名留后世,口碑犹在。有后生赞公生之所为、晚辈之忠孝,感概系之,作诗曰: 幼时命苦失双亲,兄妹低龄陷赤贫。 幸得堂前幺叔养,从兹处境运辰轮。 居家克己亲朋眷,为队廉公远小人。 儿女玄孙三辈旺,朱家代代育贤臣。 注:清明前后,应友之托,代其捉笔,为父述传,欣然承应,以表缅怀,寄字天堂,遥祝寝安!
方案(1)
方案(2)
方案(3)
方案(4)
蚂蚁A→B的路线
B
A
A’
d
A
B
A’
A
B
B
A
O
B
A
A’
r
O
4
怎样计算AB?
在Rt△AA’B中,利用勾股定理可得,
侧面展开图
其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)
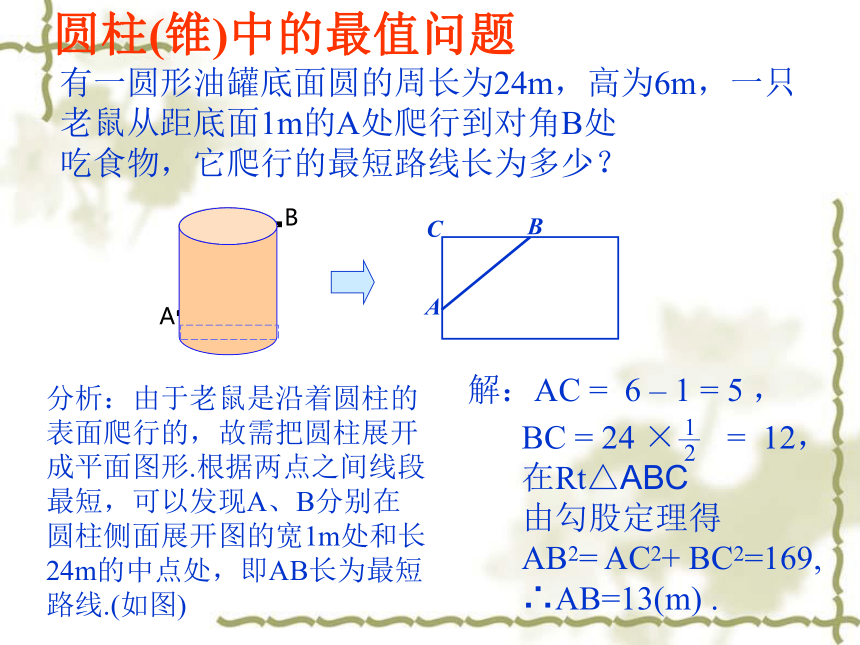
圆柱(锥)中的最值问题
有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)
解:AC
=
6
–
1
=
5
,
BC
=
24
×
=
12,
在Rt△ABC
由勾股定理得
AB2=
AC2+
BC2=169,
∴AB=13(m)
.
2
1
B
A
C
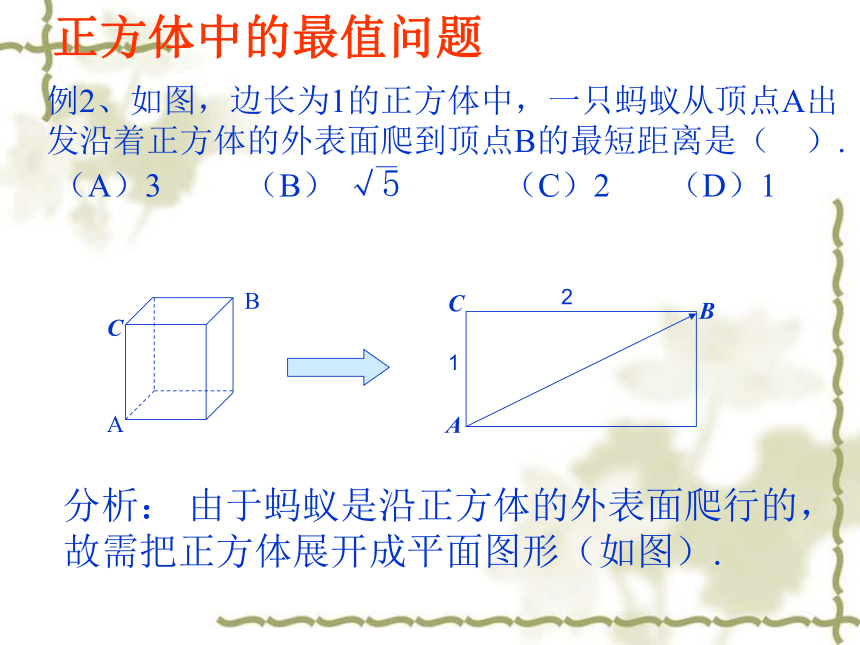
正方体中的最值问题
例2、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是(
).
(A)3
(B)
√5
(C)2
(D)1
A
B
分析:
由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).
C
A
B
C
2
1
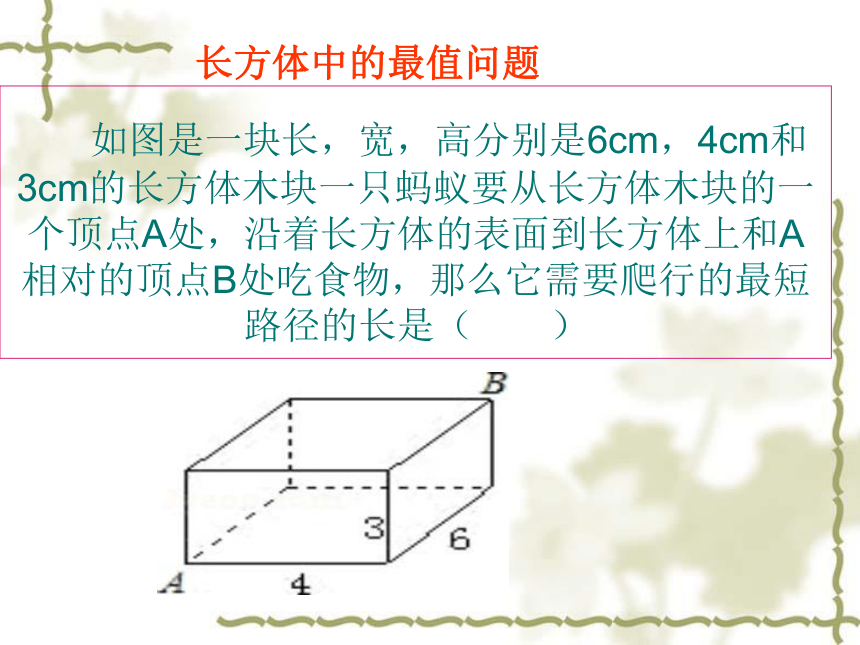
如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
长方体中的最值问题
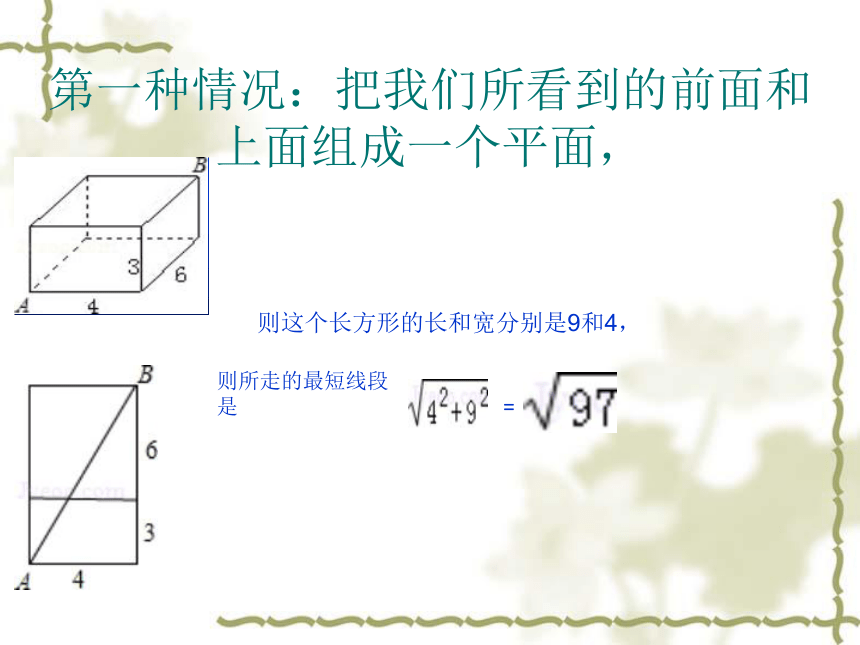
第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是9和4,
则所走的最短线段是
=
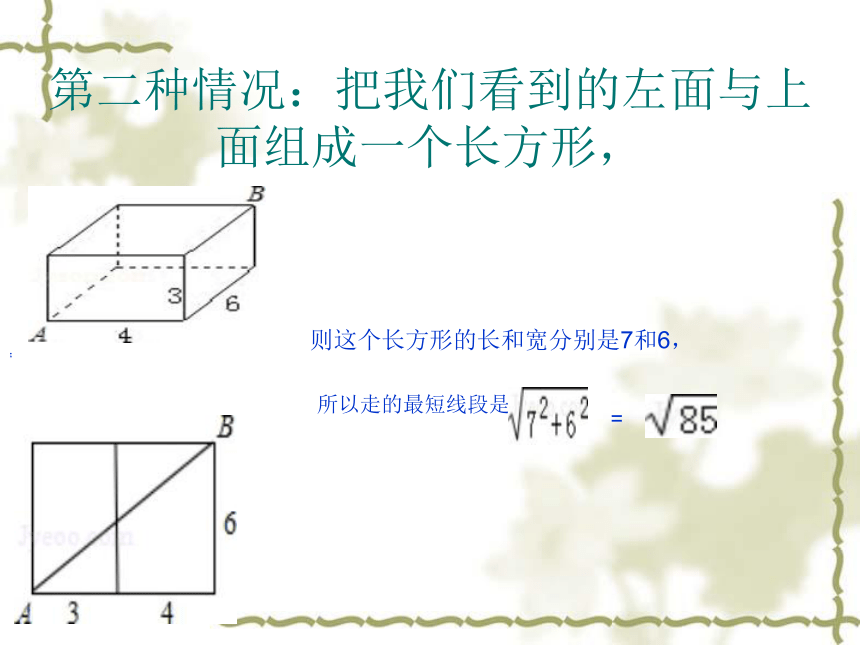
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是7和6,
所以走的最短线段是
;
=
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是10和3,
所以走的最短线段是
=
三种情况比较而言,第二种情况最短
答案:
台阶中的最值问题
例1、如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
AB=25
例4、如图,长方体的长为15
cm,宽为
10
cm,高为20
cm,点B离点C
5
cm,一只蚂蚁如果要沿着长方体的表面从点
A爬到点B,需要爬行的最短距离是多少?
?
10
20
B
A
C
15
5
长方体中的最值问题(续)
10
20
B
5
B
5
10
20
A
C
E
F
E
10
20
A
C
F
A
E
C
B
20
15
10
5
找方法、巧归纳
分别画出立体图形和对应的平面展开图
制作实体模型
归纳出所在直角三角形的两直角边的一般性规律,并记录在平面图或模型上
检测题一:如图,一只蚂蚁沿边长为a的正方体表面从顶点A爬到顶点B,则它走过的路程最短为( )
答案:
检测题二、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )
检测题三、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A沿表面爬到点B处吃食,要爬行的最短路程(π取3)是( )
如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
分析:
根据题意分析蚂蚁爬行的路线有三种情况(如图①②③
),由勾股定理可求得图1中AC1爬行的路线最短.
A
B
D
C
D1
C1
①
4
2
1
AC1
=√42+32
=√25
;
②
A
B
B1
C
A1
C1
4
1
2
AC1
=√62+12
=√37
;
A
B1
D1
D
A1
C1
③
4
1
2
AC1
=√52+22
=√29
.
检测题四
小
结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
一、台阶中的最值问题
a
b
c
A
B
a
b
c
b
c
b
A
B
C
AB=
c
二、正方体中的最值问题
A
B
C
A
B
C
2a
a
三、长方体中的最值问题
左面和上面
前面和上面
前面和右面
四、圆柱(锥)中的最值问题
A
B
B
A
C
h
底面圆周长的一半
结论:圆柱体中的最短路径为展开图中一半矩形的对角线长
勾股定理的应用之
求解几何体的最短路线长
B
A
蚂蚁怎么走最近?
例1
如图
在一个底面周长为20cm,高AA′为4cm的圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A
处爬向B处,你们想一想,蚂蚁怎么走最近?
问题情境
A
′
应有公,字财有,公元一千九百三十三年农历五月二十一生,檀林河东罗家冲人氏。于世不久,父丧母亡。家居深山,交通闭塞,徒存四壁,苦不堪言,少有田亩,衣食两难。有兄二人,相继出外谋生;公及弟妹,时龄尚幼,不谙世事,幸叔收养,方有立锥丸地,借以喘息栖身。年稍长,学耕耘,事稼穑,吃苦耐劳,得以早熟,学农活一学即会,长浑身干事气力。公虽无缘学堂,然敏学善思,苦难心悟,茅塞顿开,以精明聪敏为众所闻。是时,社会黑暗,世道无公,虽勤爬苦做、精打细算,仍忍受饥寒、难以为继。每遇春荒,不知饱饭何在;历载彻寒,未得棉衣裹身。所尝之苦,每思之,潸然泪下矣;常忆念,概莫能及哉! 然沧海桑田,星移斗转;世事更迭,其为必然。刘邓大军,挺进大别,战略反攻,序幕拉开。高山铺一役,威慑敌胆,史之所书,甚为壮怀。及至一千九百四十九年,蕲阳民众得见天日,檀林深山拥揽光明。公激情昂奋,一腔赤诚,投身新政。劳作之余,习练文化;公务之中,宣讲政策。浑身之正气,满脑之机灵,始得基层组织赏识,并于一千九百六十四年为党之一员。娶妻孙氏,亦为中共纳新。公任小队保管,饥荒连连,秋毫无犯;履会计岗位,账清目明,分厘不贪;担队长之职,身先士卒,农活拚干。红旗飘飘,尽显党员本色;忠心耿耿,常持赤子情怀。 公所事小队之公务,甚得组织褒奖,遂委以大队财经队长、村主任之职至殁年。公之于公兮,可谓披胆沥胆,催耕催种、兴修水利、抗洪救灾、急难险重,无一不冲锋在前;公之于民兮,可谓倾其所能,邻里纠纷、儿婚女嫁、稚童辍学、扶困助弱,无一不情至力竭。时至今夕,人常念道,修赤东大堤,时值腊月,严寒刺骨,公往返百余公里,徒步来回。只因里程遥偏,无宿营之处,为不违工期,遂河床挖坑、权当床铺,扁担垫身、且作床单,蓑衣覆体、是为棉被。朔风起,霜花降,焉能入睡?夜露寒,冰凝背,何以寝安?又年岁中,暴雨如注,山洪突发,河水暴涨,抗旱机泵,卷入洪流,雨水洗刷,深陷泥潭。公无视湍流之急,冒雨投河,众人感佩,悉数相帮,汗雨淋身,腾挪许久,方遂愿淘出。于公如斯,于民亦然。不乏村民难之受帮、困之受济者,口口相传,嘱晚辈、告儿孙,记公之恩德。此番情景,孰可忘怀? 公虽家境贫寒,但强而不怠,白手起家,兴室创业。常叨念古训:一粥一饭、当思来处不易,半丝半缕、恒念物力维艰。公既念之,亦践行之,严苛以求已,宽厚始待人。时年,三子女继出,家仅瓦屋两间,尤显拥蹇,添缮居室,迫在眉尖。环顾四周,窥视家底,既乏料乏粮,亦无钱无帮,境之所困,未曾吁叹,迎难而上,决然速行。乏料,遂起早贪黑,房前屋后,就地取材;乏粮,则节餐缩食,饥餐饿顿,肚中省粮;无钱无帮,即少请帮工,压减开支,片刻不歇,自行张罗。时约一周,瓦屋两间,遂以垒成。子女年幼,幸有避风挡雨之所;贤妻梦圆,方奠安居乐业之基。责任制后,公值盛年,公干之余,更是披星戴月,劲足冲天,忙碌中不知倦怠。或耕种收获、或上山打柴,或出外卖炭、或与人帮工;即便年卅,或逢阴雨,亦田间地头、山岭沟壑,忙若常态,未曾清闲。抵年末,盘收成,信心满,欣慰露,总胜乡邻几分。公足矣! 呜呼!天有不测风云,地有无端变故,人岂能避祸灾?公元一千九百九十年农历十月二十二日,公寝矣,时值壮年!檀河含悲,泗流垂首,妻儿恸哭,山乡哀号。后有人感公盛年早逝、业绩昭昭,作挽联缅怀,联曰: 天孰有道,可怜幼出寒门含辛茹苦拚事业 地岂瞒情,无愧心连集体沥胆披肝报家园 公外襄田垄,内重家道,严于教子,以身示范,邻里景仰。公时在世,节衣缩食,供孩上学,豁达乐观,涵养家风,深得族人传颂,亦得子女传承。公之两女,均受家风熏陶,品行善良,持家守道,掌衬夫家,上孝下亲,左邻右舍,堪念其范;公之一子,更得公之真传,义薄云天,高朋满座,勤奋敬业,能力过人,赢得侪辈拥戴,深为组织器重。公之孙子女,天资聪慧,术有专攻,学业有成,皆取硕士头衔,一供职于央企要位,一奉薪于鄂省机关。人常言:在世播恩爱,积德荫子孙。公之所为,应此渊源,公寝亦安矣! 噫吁!公之一生,乐善好施,帮人于急切之时;公之此世,正义凛然,挺身于危重之处。世之促,泽被子孙,香火燎原;行之难,名留后世,口碑犹在。有后生赞公生之所为、晚辈之忠孝,感概系之,作诗曰: 幼时命苦失双亲,兄妹低龄陷赤贫。 幸得堂前幺叔养,从兹处境运辰轮。 居家克己亲朋眷,为队廉公远小人。 儿女玄孙三辈旺,朱家代代育贤臣。 注:清明前后,应友之托,代其捉笔,为父述传,欣然承应,以表缅怀,寄字天堂,遥祝寝安!
方案(1)
方案(2)
方案(3)
方案(4)
蚂蚁A→B的路线
B
A
A’
d
A
B
A’
A
B
B
A
O
B
A
A’
r
O
4
怎样计算AB?
在Rt△AA’B中,利用勾股定理可得,
侧面展开图
其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)
圆柱(锥)中的最值问题
有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)
解:AC
=
6
–
1
=
5
,
BC
=
24
×
=
12,
在Rt△ABC
由勾股定理得
AB2=
AC2+
BC2=169,
∴AB=13(m)
.
2
1
B
A
C
正方体中的最值问题
例2、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是(
).
(A)3
(B)
√5
(C)2
(D)1
A
B
分析:
由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).
C
A
B
C
2
1
如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
长方体中的最值问题
第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是9和4,
则所走的最短线段是
=
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是7和6,
所以走的最短线段是
;
=
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是10和3,
所以走的最短线段是
=
三种情况比较而言,第二种情况最短
答案:
台阶中的最值问题
例1、如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
AB=25
例4、如图,长方体的长为15
cm,宽为
10
cm,高为20
cm,点B离点C
5
cm,一只蚂蚁如果要沿着长方体的表面从点
A爬到点B,需要爬行的最短距离是多少?
?
10
20
B
A
C
15
5
长方体中的最值问题(续)
10
20
B
5
B
5
10
20
A
C
E
F
E
10
20
A
C
F
A
E
C
B
20
15
10
5
找方法、巧归纳
分别画出立体图形和对应的平面展开图
制作实体模型
归纳出所在直角三角形的两直角边的一般性规律,并记录在平面图或模型上
检测题一:如图,一只蚂蚁沿边长为a的正方体表面从顶点A爬到顶点B,则它走过的路程最短为( )
答案:
检测题二、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )
检测题三、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A沿表面爬到点B处吃食,要爬行的最短路程(π取3)是( )
如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
分析:
根据题意分析蚂蚁爬行的路线有三种情况(如图①②③
),由勾股定理可求得图1中AC1爬行的路线最短.
A
B
D
C
D1
C1
①
4
2
1
AC1
=√42+32
=√25
;
②
A
B
B1
C
A1
C1
4
1
2
AC1
=√62+12
=√37
;
A
B1
D1
D
A1
C1
③
4
1
2
AC1
=√52+22
=√29
.
检测题四
小
结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
一、台阶中的最值问题
a
b
c
A
B
a
b
c
b
c
b
A
B
C
AB=
c
二、正方体中的最值问题
A
B
C
A
B
C
2a
a
三、长方体中的最值问题
左面和上面
前面和上面
前面和右面
四、圆柱(锥)中的最值问题
A
B
B
A
C
h
底面圆周长的一半
结论:圆柱体中的最短路径为展开图中一半矩形的对角线长
