苏科版七年级下册数学课件 7.1探索直线平行的条件(22张)
文档属性
| 名称 | 苏科版七年级下册数学课件 7.1探索直线平行的条件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览

文档简介
(共22张PPT)
探索直线平行的条件(2)
回顾 & 思考
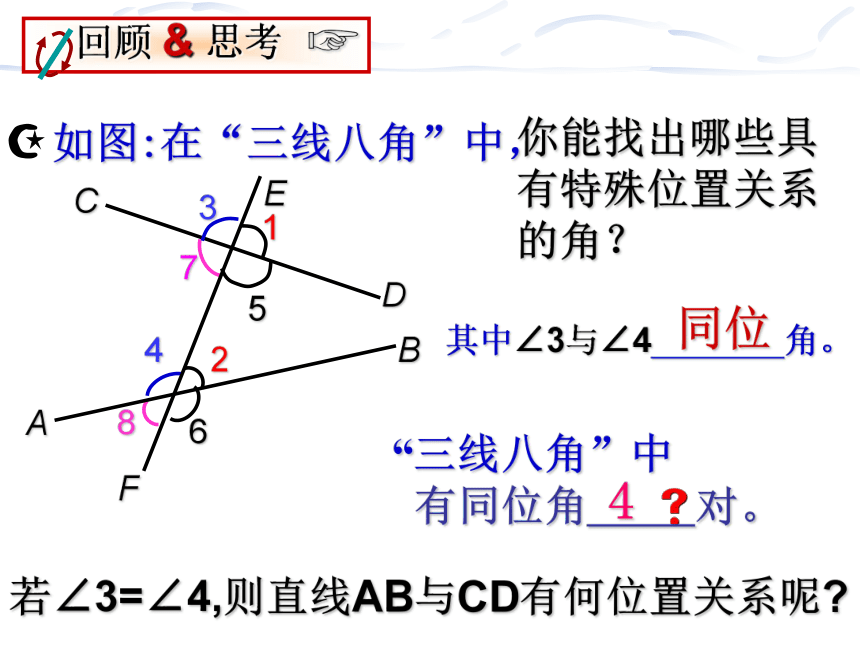
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
你能找出哪些具有特殊位置关系的角?
其中∠3与∠4 角。
同位
4
“三线八角”中
有同位角 对。
若∠3=∠4,则直线AB与CD有何位置关系呢
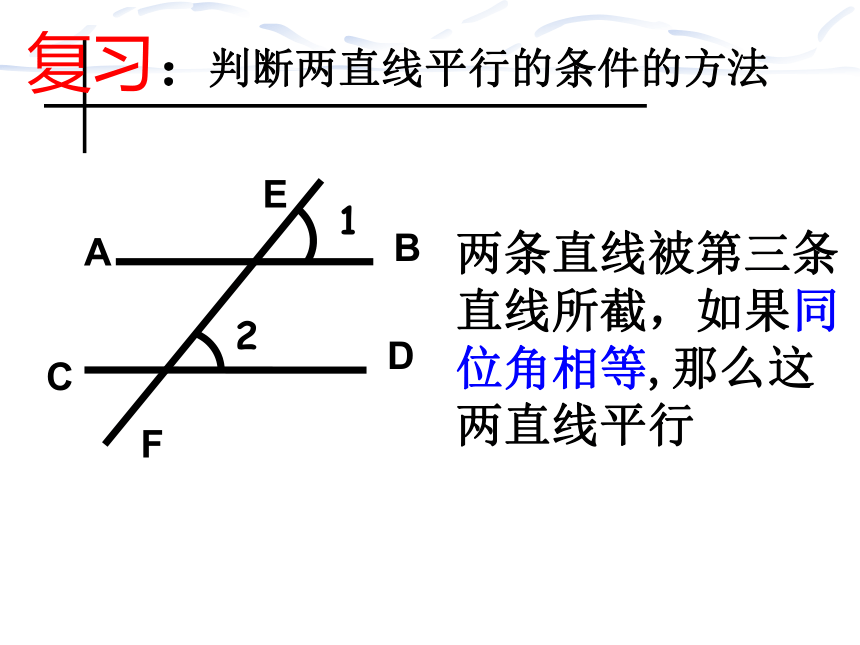
判断两直线平行的条件的方法
两条直线被第三条直线所截,如果同位角相等,那么这两直线平行
E
B
A
C
D
F
1
2
复习:
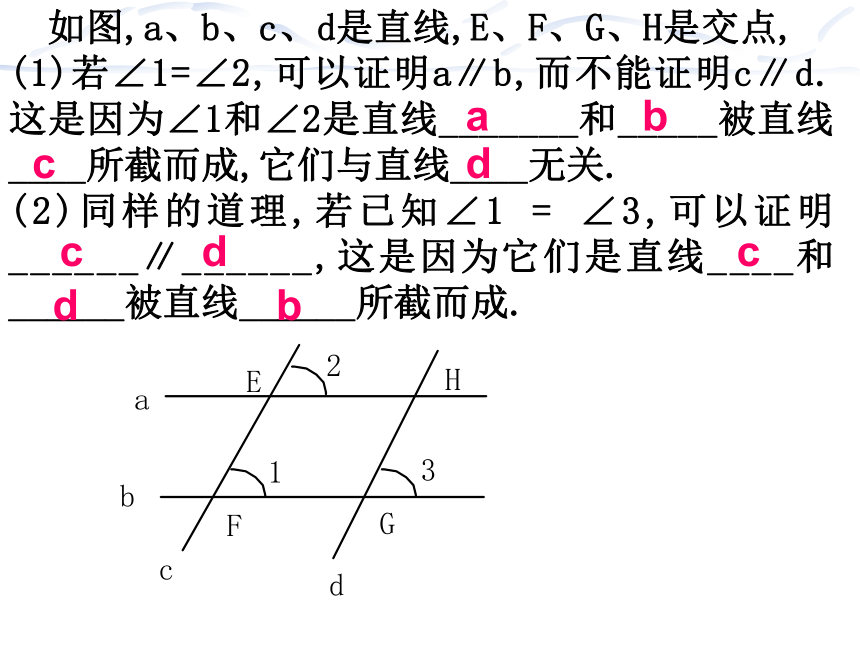
如图,a、b、c、d是直线,E、F、G、H是交点,
(1)若∠1=∠2,可以证明a∥b,而不能证明c∥d.这是因为∠1和∠2是直线_______和_____被直线____所截而成,它们与直线____无关.
(2)同样的道理,若已知∠1 = ∠3,可以证明______∥______,这是因为它们是直线____和______被直线______所截而成.
a
c
b
c
d
c
d
d
b
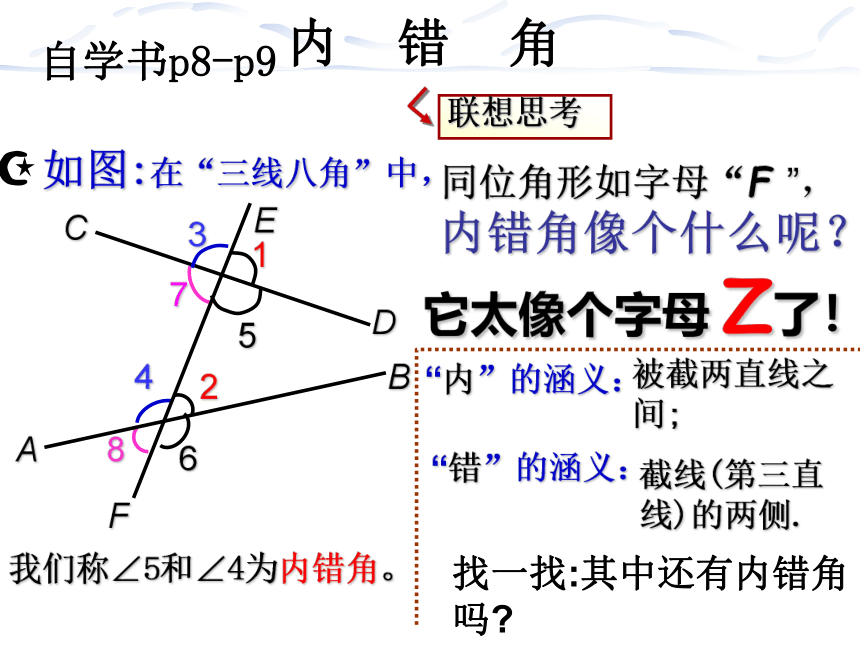
内错角像个什么呢?
我们称∠5和∠4为内错角。
联想思考
同位角形如字母“F ”,
它太像个字母 Z了!
内 错 角
“内”的涵义:
被截两直线之间;
“错”的涵义:
截线(第三直线)的两侧.
找一找:其中还有内错角吗
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
自学书p8-p9
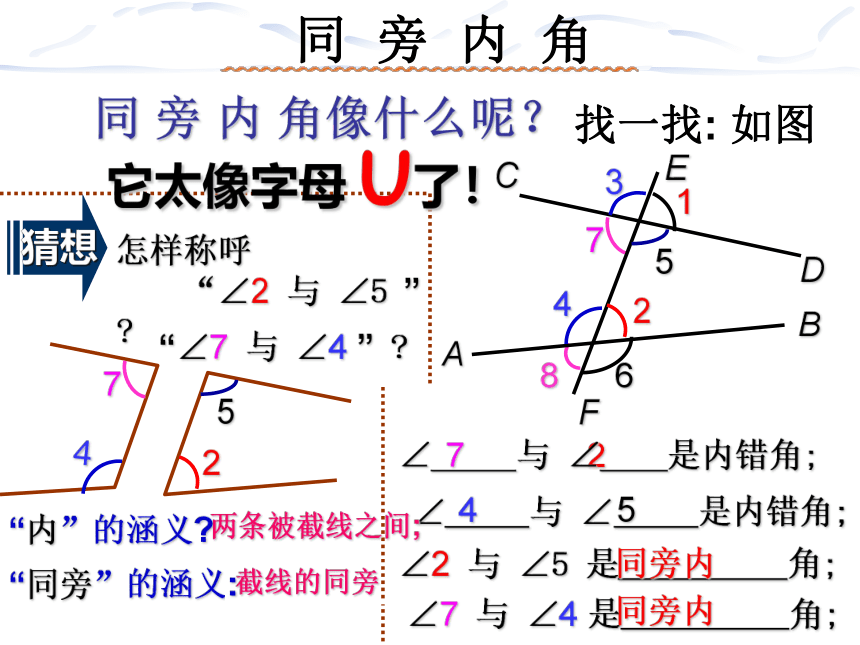
同 旁 内 角
F
1
3
7
5
2
8
6
D
C
A
B
E
4
7
2
∠ 与 ∠ 是内错角;
4
5
∠ 与 ∠ 是内错角;
5
2
7
4
∠2 与 ∠5 是 角;
∠7 与 ∠4 是 角;
同旁内
同旁内
找一找: 如图
“内”的涵义
“同旁”的涵义:
两条被截线之间;
猜想
怎样称呼
“∠2 与 ∠5 ”
“∠7 与 ∠4 ”
截线的同旁
同 旁 内 角像什么呢?
它太像字母 U了!
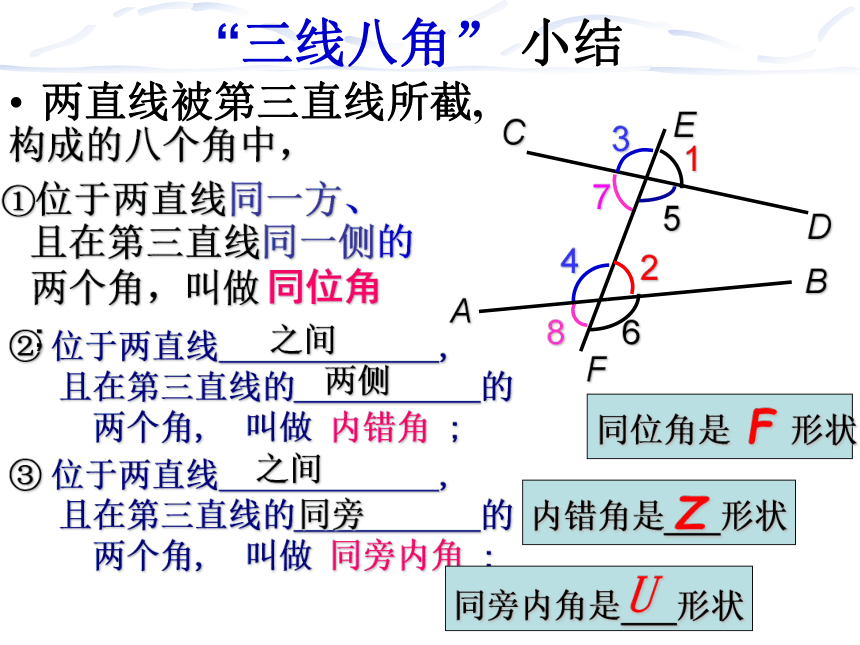
“三线八角” 小结
F
1
3
7
5
2
8
6
D
C
A
B
E
4
构成的八个角中,
两直线被第三直线所截,
①位于两直线同一方、
② 位于两直线 ,
且在第三直线的 的
两个角, 叫做 内错角 ;
且在第三直线同一侧的
两个角,叫做 ;
同位角
之间
两侧
③ 位于两直线 ,
且在第三直线的 的
两个角, 叫做 同旁内角 ;
之间
同旁
同位角是 F 形状
内错角是 形状
Z
同旁内角是 形状
U
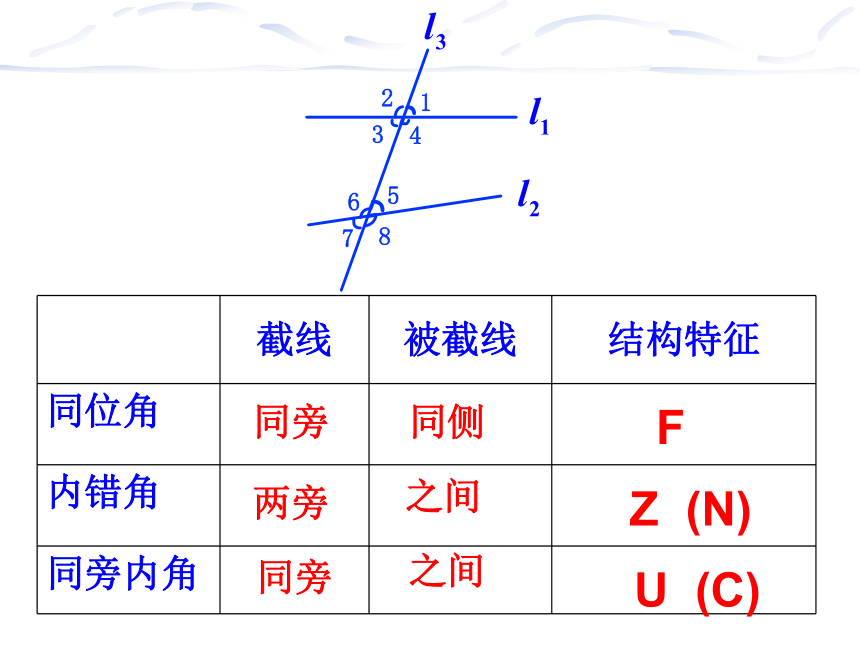
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z (N)
U (C)
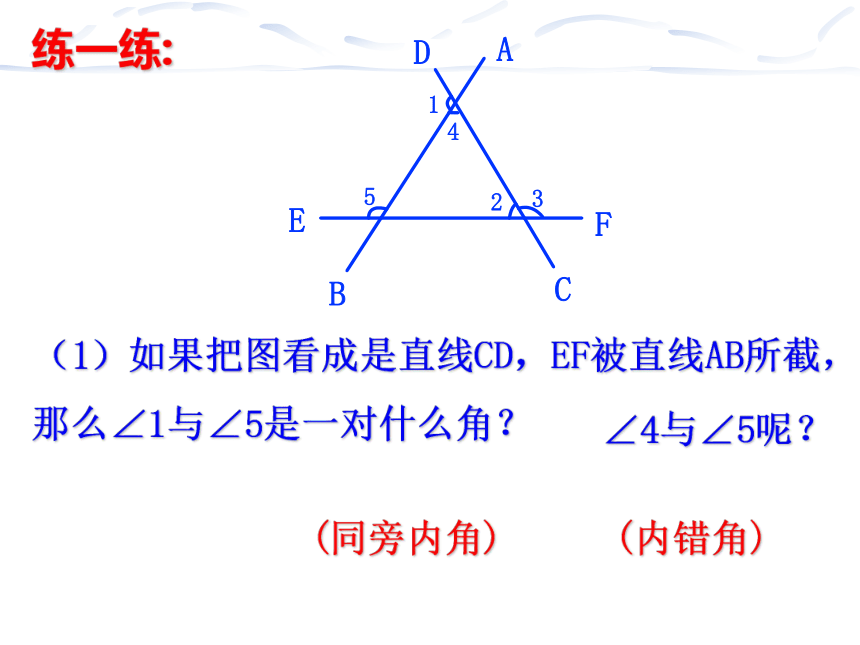
练一练:
(1)如果把图看成是直线CD,EF被直线AB所截,那么∠1与∠5是一对什么角?
∠4与∠5呢?
(同旁内角)
(内错角)
A
B
C
D
E
1
3
2
4
5
6
(1)AB、CD被BD截成的∠3和
_ 是内错角;
∠4
(2) ∠1和∠2是__角;
(3) ∠5和∠ABC是__ 角,
∠6和∠ABC是___ 角;
(4)AB、CD被AD所截成的
__和___是同旁内角.
内错
同位
同旁内
∠6
∠ADC
下图中,如果∠2=∠3,
能得出AB∥CD吗
思考
B
2
A
C
D
F
1
3
E
议一议
2
b
a
c
3
1
证明:
∵ ∠2 = ∠1,
( )
对顶角相等
∠2 = ∠3, ( )
已知
∴ ∠3 = ∠1; ( )
∴ 直线 a∥b. ( ).
等量代换
同位角相等,两直线平行.
证明思路
两直线平行
同位角相等
对顶角相等
内错角相等
B
1
2
A
D
E
F
两直线平行的条件:
两条直线被第三条直线所截,
如果内错角相等,那么这两直线平行.
C
下图中,如果∠1+∠2=180°,
能得出AB∥CD
思考
2
B
A
C
D
E
F
1
议一议
证明:
∵ ∠2 + ∠1=180o,
( )
∠1+ ∠3=180o, ( )
已知
∴ ∠3 = ∠2; ( )
∴ 直线 AB∥CD . ( ).
同角的补角相等
同位角相等,两直线平行
证明思路
两直线平行
同位角相等
两角互补
两角互补
2
B
A
C
D
E
F
1
3
邻补角定义
两直线平行的条件:
两条直线被第三条直线所截,
如果同旁内角互补,那么这两直线平行.
7
B
A
C
D
E
F
4
两直线平行 的 判定
议一议
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
应用:
如图:∠1=∠2, ∠B+∠BDE=180°.图中哪些线互相平行 为什么
A
D
B
F
C
E
1
2
思考:
当∠2=______时,DE∥BC
( )
当∠A=______时,AB∥EF
( )
∠EFC
∠FEC
内错角相等,两直线平行
同位角相等,两直线平行
1、观察右图并填空:
∠1 与 是同位角;
(2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角;
随堂练习
随堂练习
b
a
n
m
2
3
1
4
5
∠4
∠3
∠2
2、当图中各角满足下列条件时,你能指出哪两条直线平行
(1) ∠1 = ∠4;
(2) ∠2 = ∠4;
(3) ∠1 + ∠3 = 180 ;
a
b
l
m
n
1
2
3
4
a∥b.
l∥m.
l∥n .
如图所示,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么,直线AB、CD的位置关系如何?说明你的理由.
3
① 同位角有4对:
② 内错角有2对:
③ 同旁内角有2对:
∠1和∠2,
∠3和∠4,
∠5和∠6,
∠7和∠8.
∠7和∠2,
∠5和∠4.
∠7和∠4,
∠5和∠2
在三线八角中:
F
1
3
7
5
2
8
6
D
C
A
B
E
4
如何根据已知条件,说明(证明)两直线平行
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
探索直线平行的条件(2)
回顾 & 思考
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
你能找出哪些具有特殊位置关系的角?
其中∠3与∠4 角。
同位
4
“三线八角”中
有同位角 对。
若∠3=∠4,则直线AB与CD有何位置关系呢
判断两直线平行的条件的方法
两条直线被第三条直线所截,如果同位角相等,那么这两直线平行
E
B
A
C
D
F
1
2
复习:
如图,a、b、c、d是直线,E、F、G、H是交点,
(1)若∠1=∠2,可以证明a∥b,而不能证明c∥d.这是因为∠1和∠2是直线_______和_____被直线____所截而成,它们与直线____无关.
(2)同样的道理,若已知∠1 = ∠3,可以证明______∥______,这是因为它们是直线____和______被直线______所截而成.
a
c
b
c
d
c
d
d
b
内错角像个什么呢?
我们称∠5和∠4为内错角。
联想思考
同位角形如字母“F ”,
它太像个字母 Z了!
内 错 角
“内”的涵义:
被截两直线之间;
“错”的涵义:
截线(第三直线)的两侧.
找一找:其中还有内错角吗
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
自学书p8-p9
同 旁 内 角
F
1
3
7
5
2
8
6
D
C
A
B
E
4
7
2
∠ 与 ∠ 是内错角;
4
5
∠ 与 ∠ 是内错角;
5
2
7
4
∠2 与 ∠5 是 角;
∠7 与 ∠4 是 角;
同旁内
同旁内
找一找: 如图
“内”的涵义
“同旁”的涵义:
两条被截线之间;
猜想
怎样称呼
“∠2 与 ∠5 ”
“∠7 与 ∠4 ”
截线的同旁
同 旁 内 角像什么呢?
它太像字母 U了!
“三线八角” 小结
F
1
3
7
5
2
8
6
D
C
A
B
E
4
构成的八个角中,
两直线被第三直线所截,
①位于两直线同一方、
② 位于两直线 ,
且在第三直线的 的
两个角, 叫做 内错角 ;
且在第三直线同一侧的
两个角,叫做 ;
同位角
之间
两侧
③ 位于两直线 ,
且在第三直线的 的
两个角, 叫做 同旁内角 ;
之间
同旁
同位角是 F 形状
内错角是 形状
Z
同旁内角是 形状
U
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z (N)
U (C)
练一练:
(1)如果把图看成是直线CD,EF被直线AB所截,那么∠1与∠5是一对什么角?
∠4与∠5呢?
(同旁内角)
(内错角)
A
B
C
D
E
1
3
2
4
5
6
(1)AB、CD被BD截成的∠3和
_ 是内错角;
∠4
(2) ∠1和∠2是__角;
(3) ∠5和∠ABC是__ 角,
∠6和∠ABC是___ 角;
(4)AB、CD被AD所截成的
__和___是同旁内角.
内错
同位
同旁内
∠6
∠ADC
下图中,如果∠2=∠3,
能得出AB∥CD吗
思考
B
2
A
C
D
F
1
3
E
议一议
2
b
a
c
3
1
证明:
∵ ∠2 = ∠1,
( )
对顶角相等
∠2 = ∠3, ( )
已知
∴ ∠3 = ∠1; ( )
∴ 直线 a∥b. ( ).
等量代换
同位角相等,两直线平行.
证明思路
两直线平行
同位角相等
对顶角相等
内错角相等
B
1
2
A
D
E
F
两直线平行的条件:
两条直线被第三条直线所截,
如果内错角相等,那么这两直线平行.
C
下图中,如果∠1+∠2=180°,
能得出AB∥CD
思考
2
B
A
C
D
E
F
1
议一议
证明:
∵ ∠2 + ∠1=180o,
( )
∠1+ ∠3=180o, ( )
已知
∴ ∠3 = ∠2; ( )
∴ 直线 AB∥CD . ( ).
同角的补角相等
同位角相等,两直线平行
证明思路
两直线平行
同位角相等
两角互补
两角互补
2
B
A
C
D
E
F
1
3
邻补角定义
两直线平行的条件:
两条直线被第三条直线所截,
如果同旁内角互补,那么这两直线平行.
7
B
A
C
D
E
F
4
两直线平行 的 判定
议一议
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
应用:
如图:∠1=∠2, ∠B+∠BDE=180°.图中哪些线互相平行 为什么
A
D
B
F
C
E
1
2
思考:
当∠2=______时,DE∥BC
( )
当∠A=______时,AB∥EF
( )
∠EFC
∠FEC
内错角相等,两直线平行
同位角相等,两直线平行
1、观察右图并填空:
∠1 与 是同位角;
(2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角;
随堂练习
随堂练习
b
a
n
m
2
3
1
4
5
∠4
∠3
∠2
2、当图中各角满足下列条件时,你能指出哪两条直线平行
(1) ∠1 = ∠4;
(2) ∠2 = ∠4;
(3) ∠1 + ∠3 = 180 ;
a
b
l
m
n
1
2
3
4
a∥b.
l∥m.
l∥n .
如图所示,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么,直线AB、CD的位置关系如何?说明你的理由.
3
① 同位角有4对:
② 内错角有2对:
③ 同旁内角有2对:
∠1和∠2,
∠3和∠4,
∠5和∠6,
∠7和∠8.
∠7和∠2,
∠5和∠4.
∠7和∠4,
∠5和∠2
在三线八角中:
F
1
3
7
5
2
8
6
D
C
A
B
E
4
如何根据已知条件,说明(证明)两直线平行
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
