【参赛课件】数学:1.1.1《任意角》(新人教A版必修4)
文档属性
| 名称 | 【参赛课件】数学:1.1.1《任意角》(新人教A版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 123.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-01 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
1.1.1 任 意 角
第一章 三角函数
1.1 任意角和弧度制
举例实际生活中是否有些角度超出初中所学的范围?
回忆初中所学的角是如何定义?角的范围?
探讨:
①体操比赛中术语:“ 转体720°” (即转体 周),“转体 1080° ” ( 即转体 周);
2
3
逆
30
顺
30
生活实例:
②时钟快了5分钟,现要校正,需将分针怎样旋转?( 时针旋转 度)如果慢了 5 分钟,又该如何校正? ( 时针旋转 度)
③ 又如:自行车车轮;螺丝扳手;
二、新课导学
问题:
上面的实例中,已经形成了更大范围内的角,这些角显然超出了我们已有的认识范围.如何重新给出角的定义,并研究这些角的分类及记法呢?
探究任务一:角的概念
角可以看成平面内一条 绕着 从一个位置旋转到另一个位置所成的图形.
如图,一条射线由原来的位置 OA,绕着它的端点 O按逆时针方向旋转到终止位置 OB,就形成角 ,
旋转开始时的射线 OA 叫做角的 ,
OB叫 ,
射线的端点 O 叫做叫的顶点.
初中所研究的角的范围为 .
射线
端点
始边
终边
[0 , 360 )
新知:
新知:
按逆时针方向旋转所形成的角叫 角
按顺时针方向旋转所形成的角叫 角,
未作任何旋转所形成的角叫 角.
正
负
零
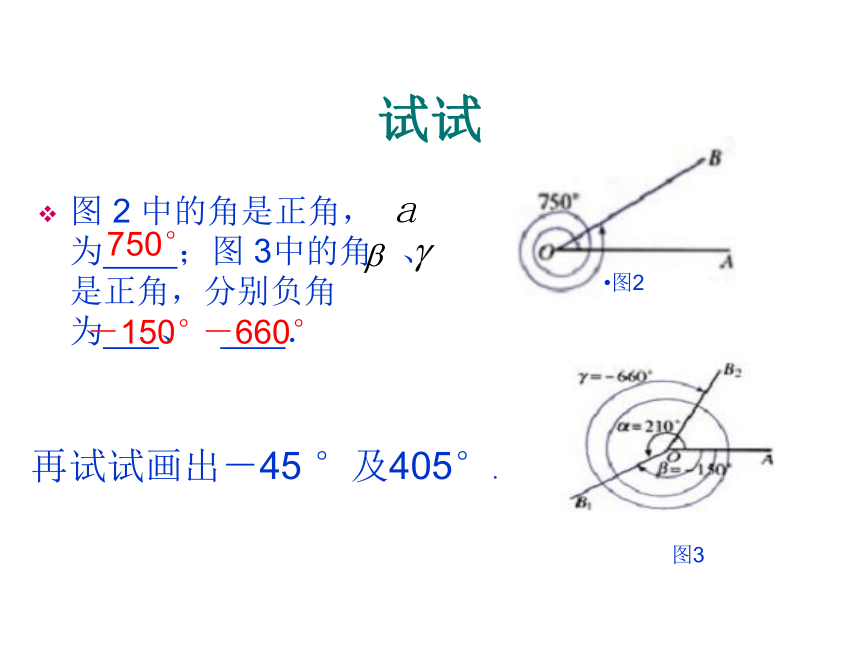
试试
图 2 中的角是正角,为 ;图 3中的角 、是正角,分别负角为 、 .
图2
图3
再试试画出-45 °及405°.
750°
-150°
-660°
反思:
角的概念推广到了 ,
包括任意大小的 角、 角和 角.
正
负
零
探究任务二:坐标系中讨论角
如何将角放入坐标系中讨论?
.
角的顶点与 重合,角的 与 Χ轴的非负半轴重合
新知:
角的终边(除端点外)在第几象限,
我们就说这个角是第几象限角.
试试:在坐标系中表示300°、390°、-330°角,并判别它们分别在第 、 、 象限.
反思:角的终边在坐标轴上,属于哪一个象限?
原点
始边
四
一
一
探究任务三:终边相同的角
问题:
与 60°终边相同的角有 、 、 、…
都可以用代数式表示为 .
420°
-300°
780°
与终边相同的角如何表示?
反思:
420°=60°+360°
-300°=60°-360°
780°=60°+2×360°
新知:
与角终边相同的角,都可用式子 k·360°+表示,k∈Z,写成集合为: .
试试:
与 390°终边相同的角
可表示为 ,
也可以表示为 .
S={ | = + k·360°,k∈Z }
S={ | = 390° + k·360°,k∈Z }
S={ | = 30° + k·360°,k∈Z }
反思:
终边相同的角 相等;
但相等的角,终边 相同;
终边相同的角有无数多个,
它们相差 360°的整数倍.
不一定
一定
例 1 在 0°~360°间,找出下列终边相同角:
(1)-150°;(2)1040°;(3)-940°
变式:写出与下列终边相同的角的集合,并写出
-720°~360°间角.
(1)120°;(2)-270°;(3)1020°
解:
-150°=210°-360 °
1040°=320 °+2×360 °
-940°=140 °-3×360 °
小组讨论:
例 2 写出终边在下列位置上的角的集合:
(1)y 轴; (2)直线y=x .
解:
在 0°~360°范围内,终边在y轴上的角有两个,即90°,270 °角。
因此,所有与90°角终边相同的角构成集合
S ={β|β= 90°+k·360°, k∈Z }
而所有与270°角终边相同的角构成集合
S =﹛β|β=270°+k·360°,k∈Z﹜
于是,终边在y轴上的角的集合
S=S ∪S ={β|β=90°+2k·180°,k∈Z﹜
∪﹛β|β=90°+180°+2k·180°,k∈Z﹜
= {β|β=90°+2k·180°,k∈Z﹜
∪﹛β|β=90°+(2k+1)·180°,k∈Z﹜
= {β|β=90°+n·180°,n∈Z﹜
小组讨论第(2)小题
注意:
0°~360°是指
小结
1.角的推广;
2.象限角的定义;
3.终边相同角的表示.
0°≤α<360°
当堂检测
1.460° 是( ).
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
2.在 0°~360°范围内,与﹣60 °终边相同的角是( ).
A.30° B.60° C.300° D.330°
3.0°~90°间的角可表示为( ).
A.{ | 0°<α<90°} B.{ | 0°≤α< 90°}
C. { | 0°≤α<90°} D. { | 0°≤α≤90°}
4. 一个角为 30°,其终边按逆时针方向旋转一周后的角的度数为 .
5. 集合 M={α|α =k×90°,k∈Z}中,各角的终边都在 .
B
C
C
390°
坐标轴上
动手试试
练 1. 如图,终边落在 OA位置时的角的集合是 :
终边落在OB 位置,且在-360°~360°内的角的集合是_ _ ;
终边落在阴影部分(含边界)的角的集合是 _.
1.1.1 任 意 角
第一章 三角函数
1.1 任意角和弧度制
举例实际生活中是否有些角度超出初中所学的范围?
回忆初中所学的角是如何定义?角的范围?
探讨:
①体操比赛中术语:“ 转体720°” (即转体 周),“转体 1080° ” ( 即转体 周);
2
3
逆
30
顺
30
生活实例:
②时钟快了5分钟,现要校正,需将分针怎样旋转?( 时针旋转 度)如果慢了 5 分钟,又该如何校正? ( 时针旋转 度)
③ 又如:自行车车轮;螺丝扳手;
二、新课导学
问题:
上面的实例中,已经形成了更大范围内的角,这些角显然超出了我们已有的认识范围.如何重新给出角的定义,并研究这些角的分类及记法呢?
探究任务一:角的概念
角可以看成平面内一条 绕着 从一个位置旋转到另一个位置所成的图形.
如图,一条射线由原来的位置 OA,绕着它的端点 O按逆时针方向旋转到终止位置 OB,就形成角 ,
旋转开始时的射线 OA 叫做角的 ,
OB叫 ,
射线的端点 O 叫做叫的顶点.
初中所研究的角的范围为 .
射线
端点
始边
终边
[0 , 360 )
新知:
新知:
按逆时针方向旋转所形成的角叫 角
按顺时针方向旋转所形成的角叫 角,
未作任何旋转所形成的角叫 角.
正
负
零
试试
图 2 中的角是正角,为 ;图 3中的角 、是正角,分别负角为 、 .
图2
图3
再试试画出-45 °及405°.
750°
-150°
-660°
反思:
角的概念推广到了 ,
包括任意大小的 角、 角和 角.
正
负
零
探究任务二:坐标系中讨论角
如何将角放入坐标系中讨论?
.
角的顶点与 重合,角的 与 Χ轴的非负半轴重合
新知:
角的终边(除端点外)在第几象限,
我们就说这个角是第几象限角.
试试:在坐标系中表示300°、390°、-330°角,并判别它们分别在第 、 、 象限.
反思:角的终边在坐标轴上,属于哪一个象限?
原点
始边
四
一
一
探究任务三:终边相同的角
问题:
与 60°终边相同的角有 、 、 、…
都可以用代数式表示为 .
420°
-300°
780°
与终边相同的角如何表示?
反思:
420°=60°+360°
-300°=60°-360°
780°=60°+2×360°
新知:
与角终边相同的角,都可用式子 k·360°+表示,k∈Z,写成集合为: .
试试:
与 390°终边相同的角
可表示为 ,
也可以表示为 .
S={ | = + k·360°,k∈Z }
S={ | = 390° + k·360°,k∈Z }
S={ | = 30° + k·360°,k∈Z }
反思:
终边相同的角 相等;
但相等的角,终边 相同;
终边相同的角有无数多个,
它们相差 360°的整数倍.
不一定
一定
例 1 在 0°~360°间,找出下列终边相同角:
(1)-150°;(2)1040°;(3)-940°
变式:写出与下列终边相同的角的集合,并写出
-720°~360°间角.
(1)120°;(2)-270°;(3)1020°
解:
-150°=210°-360 °
1040°=320 °+2×360 °
-940°=140 °-3×360 °
小组讨论:
例 2 写出终边在下列位置上的角的集合:
(1)y 轴; (2)直线y=x .
解:
在 0°~360°范围内,终边在y轴上的角有两个,即90°,270 °角。
因此,所有与90°角终边相同的角构成集合
S ={β|β= 90°+k·360°, k∈Z }
而所有与270°角终边相同的角构成集合
S =﹛β|β=270°+k·360°,k∈Z﹜
于是,终边在y轴上的角的集合
S=S ∪S ={β|β=90°+2k·180°,k∈Z﹜
∪﹛β|β=90°+180°+2k·180°,k∈Z﹜
= {β|β=90°+2k·180°,k∈Z﹜
∪﹛β|β=90°+(2k+1)·180°,k∈Z﹜
= {β|β=90°+n·180°,n∈Z﹜
小组讨论第(2)小题
注意:
0°~360°是指
小结
1.角的推广;
2.象限角的定义;
3.终边相同角的表示.
0°≤α<360°
当堂检测
1.460° 是( ).
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
2.在 0°~360°范围内,与﹣60 °终边相同的角是( ).
A.30° B.60° C.300° D.330°
3.0°~90°间的角可表示为( ).
A.{ | 0°<α<90°} B.{ | 0°≤α< 90°}
C. { | 0°≤α<90°} D. { | 0°≤α≤90°}
4. 一个角为 30°,其终边按逆时针方向旋转一周后的角的度数为 .
5. 集合 M={α|α =k×90°,k∈Z}中,各角的终边都在 .
B
C
C
390°
坐标轴上
动手试试
练 1. 如图,终边落在 OA位置时的角的集合是 :
终边落在OB 位置,且在-360°~360°内的角的集合是_ _ ;
终边落在阴影部分(含边界)的角的集合是 _.
