2020-2021学年北师大版七年级数学下册第四章三角形 单元测试题(Word版 含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第四章三角形 单元测试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 317.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 11:40:44 | ||
图片预览




文档简介
2020-2021学年北师大版七年级数学下册第四章 三角形 单元测试题
(时间:120分钟 满分:150分)
A卷(共100分)
一、选择题(本大题共10个小题,每小题3分.)
1.下列各组数不可能是一个三角形的边长的是( )
A.1,2,3 B.4,4,4 C.6,6,8 D.7,8,9
2.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
A.DE是△ABE的高 B.DE是△BCD的高
C.AC是△ABC的高 D.AD是△ACD的高
3.下列说法不正确的是( )
A.全等三角形的对应边和对应角相等 B.全等三角形的面积相等
C.全等三角形的周长相等 D.面积相等的三角形是全等三角形
4.直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是( )
A.22.5° B.45° C.67.5° D.135°
5.如图,△ABC≌△EBD,∠E=50°,∠D=62°,则∠ABC的度数是( )
A.68° B.62° C.60° D.50°
6.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
7.如图,如果AD∥BC,AD=BC,AC与BD相交于O点,那么图中的全等三角形一共有( )
A.3对 B.4对 C.5对 D.6对
8.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
9.如图,在△ABC中,已知点D,E分别为边BC,AD上的中点,且S△ABC=4 cm2,则S△BEC的值为( )
A.2 cm2 B.1 cm2 C.0.5 cm2 D.0.25 cm2
10.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c B.b+c C.a-b+c D.a+b-c
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.△ABC中,当∠A∶∠B∶∠C=1∶2∶3时,这个三角形是_____三角形.(填“锐角”“直角”或“钝角”)
12.若△ABC≌△DEF,△DEF的周长为12 cm,且AB=4 cm,BC=3 cm,则DF的长为_____.
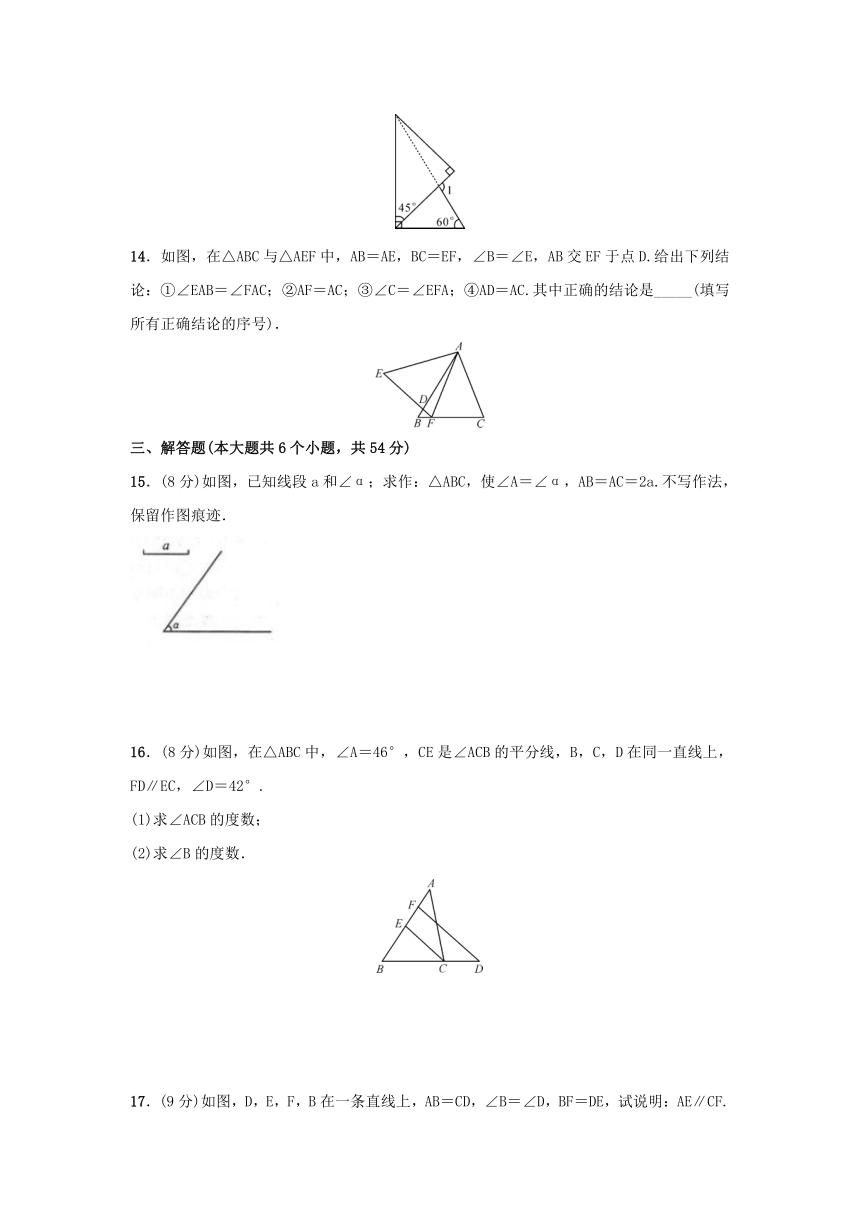
13.如果将一副三角板按如图方式叠放,那么∠1=_____.
14.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.给出下列结论:①∠EAB=∠FAC;②AF=AC;③∠C=∠EFA;④AD=AC.其中正确的结论是_____(填写所有正确结论的序号).
三、解答题(本大题共6个小题,共54分)
15.(8分)如图,已知线段a和∠α;求作:△ABC,使∠A=∠α,AB=AC=2a.不写作法,保留作图痕迹.
16.(8分)如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一直线上,FD∥EC,∠D=42°.
(1)求∠ACB的度数;
(2)求∠B的度数.
17.(9分)如图,D,E,F,B在一条直线上,AB=CD,∠B=∠D,BF=DE,试说明:AE∥CF.
18.(9分)如图,在方格纸中,△PQR的三个顶点及A,B,C,D,E五个点都在小方格的顶点上.现以A,B,C,D,E中的三个点为顶点画三角形.
(1)在图1中画出一个三角形与△PQR全等;
(2)在图2中画出一个三角形与△PQR面积相等但不全等.
19.(10分)如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于点E.
(1)试说明:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长.
20.(10分)如图,在△ABC中,∠A=60°,角平分线BD,CE交于点O.
(1)求∠BOC的度数;
(2)点F在BC上,BF=BE,试说明:△COD≌△COF;
(3)BE,CD,BC三条线段之间有怎样的数量关系?请直接写出结果.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在题中的横线上)
21.一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是_____.
22.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,EF=6,BG=3,DH=4,计算图中实线所围成的图形的面积S是_____.
23.如图,在△ABC中,∠A=84°,点O是∠ABC,∠ACB平分线的交点,点P是∠BOC,∠OCB平分线的交点.若∠P=100°,则∠ACB的度数是_____.
24.已知AD是△ABC的高,且∠BAD=35°,∠CAD=60°,则∠BAC的度数是_____.
25.如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E,F分别是CB,CD上的点,且∠EAF=70°,下列说法正确的是_____.(填写正确的序号)
①DF=BE;②△ADF≌△ABE;③FA平分∠DFE;④AE平分∠FAB;⑤BE+DF=EF;⑥CF+CE>FD+EB.
二、解答题(本大题共3个小题,共30分)
26.(8分)如图1,在△ABC中,∠ACB=90°,CA=CB,点D在CA上,点E在CB上,且CD=CE,则易证得AD=BE.
(1)若把△DCE绕点C顺时针旋转一定角度(如图2),连接AD,BE,判断AD与BE是否相等?若相等,请证明;若不相等,请说明理由;
(2)若把△ACB和△CDE都改为一般等腰三角形(如图3),且∠ACB=∠DCE,则AD=BE还成立吗?
图1 图2 图3
27.(10分)探究与发现:
如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样的图形叫做“规形图”,那么在这个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY,XZ恰好经过点B,C.若∠A=50°,则∠ABX+∠ACX=_____;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1,G2,…,G9.若∠BDC=140°,∠BG1C=77°,求∠A的度数.
28.(12分)(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于点D,CE⊥m于点E,求证:DE=BD+CE;
(2)拓展:如图2,将(1)中的条件改为在△ABC中,AB=AC,D,A,E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图3,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
图1 图2 图3
参考答案
2020-2021学年北师大版七年级数学下册第四章 三角形 单元测试题
(时间:120分钟 满分:150分)
A卷(共100分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
D
A
A
D
B
A
A
D
1.下列各组数不可能是一个三角形的边长的是(A)
A.1,2,3 B.4,4,4 C.6,6,8 D.7,8,9
2.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是(A)
A.DE是△ABE的高 B.DE是△BCD的高
C.AC是△ABC的高 D.AD是△ACD的高
3.下列说法不正确的是(D)
A.全等三角形的对应边和对应角相等 B.全等三角形的面积相等
C.全等三角形的周长相等 D.面积相等的三角形是全等三角形
4.直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是(A)
A.22.5° B.45° C.67.5° D.135°
5.如图,△ABC≌△EBD,∠E=50°,∠D=62°,则∠ABC的度数是(A)
A.68° B.62° C.60° D.50°
6.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD(D)
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
7.如图,如果AD∥BC,AD=BC,AC与BD相交于O点,那么图中的全等三角形一共有(B)
A.3对 B.4对 C.5对 D.6对
8.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=(A)
A.75° B.80° C.85° D.90°
9.如图,在△ABC中,已知点D,E分别为边BC,AD上的中点,且S△ABC=4 cm2,则S△BEC的值为(A)
A.2 cm2 B.1 cm2 C.0.5 cm2 D.0.25 cm2
10.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为(D)
A.a+c B.b+c C.a-b+c D.a+b-c
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.△ABC中,当∠A∶∠B∶∠C=1∶2∶3时,这个三角形是直角三角形.(填“锐角”“直角”或“钝角”)
12.若△ABC≌△DEF,△DEF的周长为12 cm,且AB=4 cm,BC=3 cm,则DF的长为5_cm.
13.如果将一副三角板按如图方式叠放,那么∠1=105°.
14.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.给出下列结论:①∠EAB=∠FAC;②AF=AC;③∠C=∠EFA;④AD=AC.其中正确的结论是①②③(填写所有正确结论的序号).
三、解答题(本大题共6个小题,共54分)
15.(8分)如图,已知线段a和∠α;求作:△ABC,使∠A=∠α,AB=AC=2a.不写作法,保留作图痕迹.
解:如图所示.
16.(8分)如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一直线上,FD∥EC,∠D=42°.
(1)求∠ACB的度数;
(2)求∠B的度数.
解:(1)∵FD∥EC,∠D=42°,∴∠BCE=42°.
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°.
(2)∵∠A=46°,
∴∠B=180°-84°-46°=50°.
17.(9分)如图,D,E,F,B在一条直线上,AB=CD,∠B=∠D,BF=DE,试说明:AE∥CF.
解:∵BF=DE,
∴BF+EF=DE+EF,即BE=DF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
∴∠AEB=∠CFD.∴AE∥CF.
18.(9分)如图,在方格纸中,△PQR的三个顶点及A,B,C,D,E五个点都在小方格的顶点上.现以A,B,C,D,E中的三个点为顶点画三角形.
(1)在图1中画出一个三角形与△PQR全等;
(2)在图2中画出一个三角形与△PQR面积相等但不全等.
解:
19.(10分)如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于点E.
(1)试说明:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长.
解:(1)∵∠C=90°,DE⊥AB,∴∠C=∠AED=90°.
在△ACD和△AED中,
∴△ACD≌△AED(AAS).
∴AC=AE.
(2)由(1),得△ACD≌△AED,∴DC=DE.
∵S△ACB=S△ACD+S△ADB,
∴S△ACB=AC·CD+AB·DE.
又∵AC=8,AB=10,且△ABC的面积等于24,
∴24=×8×CD+×10×DE.
∴DE=.
20.(10分)如图,在△ABC中,∠A=60°,角平分线BD,CE交于点O.
(1)求∠BOC的度数;
(2)点F在BC上,BF=BE,试说明:△COD≌△COF;
(3)BE,CD,BC三条线段之间有怎样的数量关系?请直接写出结果.
解:(1)在△ABC中,∠A=60°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×(180°-60°)=60°.
∴∠BOC=180°-60°=120°.
(2)∵BD平分∠ABC,∴∠EBO=∠FBO.
在△OBE和△OBF中,
∴△OBE≌△OBF(SAS).
∴∠BOE=∠BOF.
∵∠BOC=120°,∴∠BOE=60°.
∴∠BOF=∠COF=∠COD=60°.
在△COD和△COF中,
∴△COD≌△COF(ASA).
(3)BC=BE+CD.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在题中的横线上)
21.一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是16或17.
22.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,EF=6,BG=3,DH=4,计算图中实线所围成的图形的面积S是50.
23.如图,在△ABC中,∠A=84°,点O是∠ABC,∠ACB平分线的交点,点P是∠BOC,∠OCB平分线的交点.若∠P=100°,则∠ACB的度数是56°.
24.已知AD是△ABC的高,且∠BAD=35°,∠CAD=60°,则∠BAC的度数是95°或25°.
25.如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E,F分别是CB,CD上的点,且∠EAF=70°,下列说法正确的是③⑤⑥.(填写正确的序号)
①DF=BE;②△ADF≌△ABE;③FA平分∠DFE;④AE平分∠FAB;⑤BE+DF=EF;⑥CF+CE>FD+EB.
二、解答题(本大题共3个小题,共30分)
26.(8分)如图1,在△ABC中,∠ACB=90°,CA=CB,点D在CA上,点E在CB上,且CD=CE,则易证得AD=BE.
(1)若把△DCE绕点C顺时针旋转一定角度(如图2),连接AD,BE,判断AD与BE是否相等?若相等,请证明;若不相等,请说明理由;
(2)若把△ACB和△CDE都改为一般等腰三角形(如图3),且∠ACB=∠DCE,则AD=BE还成立吗?
图1 图2 图3
解:(1)AD=BE.
理由:∵∠ACD=∠ACB-∠DCB,∠ACB=∠DCE=90°,
∴∠ACD=∠DCE-∠DCB.
∵∠BCE=∠DCE-∠DCB,∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).∴AD=BE.
(2)AD=BE还成立.
理由:∵∠ACD=∠ACB-∠DCB,∠ACB=∠DCE,
∴∠ACD=∠DCE-∠DCB.
∵∠BCE=∠DCE-∠DCB,∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).∴AD=BE.
27.(10分)探究与发现:
如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样的图形叫做“规形图”,那么在这个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY,XZ恰好经过点B,C.若∠A=50°,则∠ABX+∠ACX=40°;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1,G2,…,G9.若∠BDC=140°,∠BG1C=77°,求∠A的度数.
图1 图2 图3 图4
解:(1)连接AD并延长至点F,
则∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,
又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠BAC+∠B+∠C.
(2)②由(1)的结论易得∠DBE=∠A+∠ADB+∠AEB,
∴∠ADB+∠AEB=∠DBE-∠A=80°.
又∵∠DCE=(∠ADB+∠AEB)+∠A,
∴∠DCE=×80°+50°=90°.
③设∠A为x°,则∠ABD+∠ACD=140°-x°.
∵∠BG1C=(∠ABD+∠ACD)+∠A,∠BG1C=77°,
∴(140-x)+x=77,解得x=70.
∴∠A=70°.
28.(12分)(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于点D,CE⊥m于点E,求证:DE=BD+CE;
(2)拓展:如图2,将(1)中的条件改为在△ABC中,AB=AC,D,A,E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图3,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
图1 图2 图3
解:(1)证明:∵BD⊥m,CE⊥m,
∴∠BDA=∠AEC=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴AE=BD,AD=CE.
∴DE=AE+AD=BD+CE.
(2)结论DE=BD+CE成立.
证明:∵∠BDA=∠BAC=α,
∴∠ABD+∠BAD=∠BAD+∠CAE=180°-α.
∴∠CAE=∠ABD.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴AE=BD,AD=CE.
∴DE=AE+AD=BD+CE.
(3)∵∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,
∴∠CAE=∠ABD.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS).
∴S△ABD=S△CAE.
设△ABC的底边BC上的高为h,则△ACF的底边CF上的高为h,
则S△ABC=BC·h,S△ACF=CF·h.
∵BC=2CF,S△ABC=12,
∴S△ACF=S△ABC=6.
∵S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6,
∴△ABD与△CEF的面积之和为6.
(时间:120分钟 满分:150分)
A卷(共100分)
一、选择题(本大题共10个小题,每小题3分.)
1.下列各组数不可能是一个三角形的边长的是( )
A.1,2,3 B.4,4,4 C.6,6,8 D.7,8,9
2.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
A.DE是△ABE的高 B.DE是△BCD的高
C.AC是△ABC的高 D.AD是△ACD的高
3.下列说法不正确的是( )
A.全等三角形的对应边和对应角相等 B.全等三角形的面积相等
C.全等三角形的周长相等 D.面积相等的三角形是全等三角形
4.直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是( )
A.22.5° B.45° C.67.5° D.135°
5.如图,△ABC≌△EBD,∠E=50°,∠D=62°,则∠ABC的度数是( )
A.68° B.62° C.60° D.50°
6.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
7.如图,如果AD∥BC,AD=BC,AC与BD相交于O点,那么图中的全等三角形一共有( )
A.3对 B.4对 C.5对 D.6对
8.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
9.如图,在△ABC中,已知点D,E分别为边BC,AD上的中点,且S△ABC=4 cm2,则S△BEC的值为( )
A.2 cm2 B.1 cm2 C.0.5 cm2 D.0.25 cm2
10.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c B.b+c C.a-b+c D.a+b-c
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.△ABC中,当∠A∶∠B∶∠C=1∶2∶3时,这个三角形是_____三角形.(填“锐角”“直角”或“钝角”)
12.若△ABC≌△DEF,△DEF的周长为12 cm,且AB=4 cm,BC=3 cm,则DF的长为_____.
13.如果将一副三角板按如图方式叠放,那么∠1=_____.
14.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.给出下列结论:①∠EAB=∠FAC;②AF=AC;③∠C=∠EFA;④AD=AC.其中正确的结论是_____(填写所有正确结论的序号).
三、解答题(本大题共6个小题,共54分)
15.(8分)如图,已知线段a和∠α;求作:△ABC,使∠A=∠α,AB=AC=2a.不写作法,保留作图痕迹.
16.(8分)如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一直线上,FD∥EC,∠D=42°.
(1)求∠ACB的度数;
(2)求∠B的度数.
17.(9分)如图,D,E,F,B在一条直线上,AB=CD,∠B=∠D,BF=DE,试说明:AE∥CF.
18.(9分)如图,在方格纸中,△PQR的三个顶点及A,B,C,D,E五个点都在小方格的顶点上.现以A,B,C,D,E中的三个点为顶点画三角形.
(1)在图1中画出一个三角形与△PQR全等;
(2)在图2中画出一个三角形与△PQR面积相等但不全等.
19.(10分)如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于点E.
(1)试说明:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长.
20.(10分)如图,在△ABC中,∠A=60°,角平分线BD,CE交于点O.
(1)求∠BOC的度数;
(2)点F在BC上,BF=BE,试说明:△COD≌△COF;
(3)BE,CD,BC三条线段之间有怎样的数量关系?请直接写出结果.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在题中的横线上)
21.一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是_____.
22.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,EF=6,BG=3,DH=4,计算图中实线所围成的图形的面积S是_____.
23.如图,在△ABC中,∠A=84°,点O是∠ABC,∠ACB平分线的交点,点P是∠BOC,∠OCB平分线的交点.若∠P=100°,则∠ACB的度数是_____.
24.已知AD是△ABC的高,且∠BAD=35°,∠CAD=60°,则∠BAC的度数是_____.
25.如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E,F分别是CB,CD上的点,且∠EAF=70°,下列说法正确的是_____.(填写正确的序号)
①DF=BE;②△ADF≌△ABE;③FA平分∠DFE;④AE平分∠FAB;⑤BE+DF=EF;⑥CF+CE>FD+EB.
二、解答题(本大题共3个小题,共30分)
26.(8分)如图1,在△ABC中,∠ACB=90°,CA=CB,点D在CA上,点E在CB上,且CD=CE,则易证得AD=BE.
(1)若把△DCE绕点C顺时针旋转一定角度(如图2),连接AD,BE,判断AD与BE是否相等?若相等,请证明;若不相等,请说明理由;
(2)若把△ACB和△CDE都改为一般等腰三角形(如图3),且∠ACB=∠DCE,则AD=BE还成立吗?
图1 图2 图3
27.(10分)探究与发现:
如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样的图形叫做“规形图”,那么在这个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY,XZ恰好经过点B,C.若∠A=50°,则∠ABX+∠ACX=_____;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1,G2,…,G9.若∠BDC=140°,∠BG1C=77°,求∠A的度数.
28.(12分)(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于点D,CE⊥m于点E,求证:DE=BD+CE;
(2)拓展:如图2,将(1)中的条件改为在△ABC中,AB=AC,D,A,E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图3,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
图1 图2 图3
参考答案
2020-2021学年北师大版七年级数学下册第四章 三角形 单元测试题
(时间:120分钟 满分:150分)
A卷(共100分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
D
A
A
D
B
A
A
D
1.下列各组数不可能是一个三角形的边长的是(A)
A.1,2,3 B.4,4,4 C.6,6,8 D.7,8,9
2.如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是(A)
A.DE是△ABE的高 B.DE是△BCD的高
C.AC是△ABC的高 D.AD是△ACD的高
3.下列说法不正确的是(D)
A.全等三角形的对应边和对应角相等 B.全等三角形的面积相等
C.全等三角形的周长相等 D.面积相等的三角形是全等三角形
4.直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是(A)
A.22.5° B.45° C.67.5° D.135°
5.如图,△ABC≌△EBD,∠E=50°,∠D=62°,则∠ABC的度数是(A)
A.68° B.62° C.60° D.50°
6.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD(D)
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
7.如图,如果AD∥BC,AD=BC,AC与BD相交于O点,那么图中的全等三角形一共有(B)
A.3对 B.4对 C.5对 D.6对
8.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=(A)
A.75° B.80° C.85° D.90°
9.如图,在△ABC中,已知点D,E分别为边BC,AD上的中点,且S△ABC=4 cm2,则S△BEC的值为(A)
A.2 cm2 B.1 cm2 C.0.5 cm2 D.0.25 cm2
10.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为(D)
A.a+c B.b+c C.a-b+c D.a+b-c
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.△ABC中,当∠A∶∠B∶∠C=1∶2∶3时,这个三角形是直角三角形.(填“锐角”“直角”或“钝角”)
12.若△ABC≌△DEF,△DEF的周长为12 cm,且AB=4 cm,BC=3 cm,则DF的长为5_cm.
13.如果将一副三角板按如图方式叠放,那么∠1=105°.
14.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.给出下列结论:①∠EAB=∠FAC;②AF=AC;③∠C=∠EFA;④AD=AC.其中正确的结论是①②③(填写所有正确结论的序号).
三、解答题(本大题共6个小题,共54分)
15.(8分)如图,已知线段a和∠α;求作:△ABC,使∠A=∠α,AB=AC=2a.不写作法,保留作图痕迹.
解:如图所示.
16.(8分)如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一直线上,FD∥EC,∠D=42°.
(1)求∠ACB的度数;
(2)求∠B的度数.
解:(1)∵FD∥EC,∠D=42°,∴∠BCE=42°.
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°.
(2)∵∠A=46°,
∴∠B=180°-84°-46°=50°.
17.(9分)如图,D,E,F,B在一条直线上,AB=CD,∠B=∠D,BF=DE,试说明:AE∥CF.
解:∵BF=DE,
∴BF+EF=DE+EF,即BE=DF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
∴∠AEB=∠CFD.∴AE∥CF.
18.(9分)如图,在方格纸中,△PQR的三个顶点及A,B,C,D,E五个点都在小方格的顶点上.现以A,B,C,D,E中的三个点为顶点画三角形.
(1)在图1中画出一个三角形与△PQR全等;
(2)在图2中画出一个三角形与△PQR面积相等但不全等.
解:
19.(10分)如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于点E.
(1)试说明:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长.
解:(1)∵∠C=90°,DE⊥AB,∴∠C=∠AED=90°.
在△ACD和△AED中,
∴△ACD≌△AED(AAS).
∴AC=AE.
(2)由(1),得△ACD≌△AED,∴DC=DE.
∵S△ACB=S△ACD+S△ADB,
∴S△ACB=AC·CD+AB·DE.
又∵AC=8,AB=10,且△ABC的面积等于24,
∴24=×8×CD+×10×DE.
∴DE=.
20.(10分)如图,在△ABC中,∠A=60°,角平分线BD,CE交于点O.
(1)求∠BOC的度数;
(2)点F在BC上,BF=BE,试说明:△COD≌△COF;
(3)BE,CD,BC三条线段之间有怎样的数量关系?请直接写出结果.
解:(1)在△ABC中,∠A=60°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×(180°-60°)=60°.
∴∠BOC=180°-60°=120°.
(2)∵BD平分∠ABC,∴∠EBO=∠FBO.
在△OBE和△OBF中,
∴△OBE≌△OBF(SAS).
∴∠BOE=∠BOF.
∵∠BOC=120°,∴∠BOE=60°.
∴∠BOF=∠COF=∠COD=60°.
在△COD和△COF中,
∴△COD≌△COF(ASA).
(3)BC=BE+CD.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在题中的横线上)
21.一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是16或17.
22.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,EF=6,BG=3,DH=4,计算图中实线所围成的图形的面积S是50.
23.如图,在△ABC中,∠A=84°,点O是∠ABC,∠ACB平分线的交点,点P是∠BOC,∠OCB平分线的交点.若∠P=100°,则∠ACB的度数是56°.
24.已知AD是△ABC的高,且∠BAD=35°,∠CAD=60°,则∠BAC的度数是95°或25°.
25.如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E,F分别是CB,CD上的点,且∠EAF=70°,下列说法正确的是③⑤⑥.(填写正确的序号)
①DF=BE;②△ADF≌△ABE;③FA平分∠DFE;④AE平分∠FAB;⑤BE+DF=EF;⑥CF+CE>FD+EB.
二、解答题(本大题共3个小题,共30分)
26.(8分)如图1,在△ABC中,∠ACB=90°,CA=CB,点D在CA上,点E在CB上,且CD=CE,则易证得AD=BE.
(1)若把△DCE绕点C顺时针旋转一定角度(如图2),连接AD,BE,判断AD与BE是否相等?若相等,请证明;若不相等,请说明理由;
(2)若把△ACB和△CDE都改为一般等腰三角形(如图3),且∠ACB=∠DCE,则AD=BE还成立吗?
图1 图2 图3
解:(1)AD=BE.
理由:∵∠ACD=∠ACB-∠DCB,∠ACB=∠DCE=90°,
∴∠ACD=∠DCE-∠DCB.
∵∠BCE=∠DCE-∠DCB,∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).∴AD=BE.
(2)AD=BE还成立.
理由:∵∠ACD=∠ACB-∠DCB,∠ACB=∠DCE,
∴∠ACD=∠DCE-∠DCB.
∵∠BCE=∠DCE-∠DCB,∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).∴AD=BE.
27.(10分)探究与发现:
如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样的图形叫做“规形图”,那么在这个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY,XZ恰好经过点B,C.若∠A=50°,则∠ABX+∠ACX=40°;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1,G2,…,G9.若∠BDC=140°,∠BG1C=77°,求∠A的度数.
图1 图2 图3 图4
解:(1)连接AD并延长至点F,
则∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,
又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠BAC+∠B+∠C.
(2)②由(1)的结论易得∠DBE=∠A+∠ADB+∠AEB,
∴∠ADB+∠AEB=∠DBE-∠A=80°.
又∵∠DCE=(∠ADB+∠AEB)+∠A,
∴∠DCE=×80°+50°=90°.
③设∠A为x°,则∠ABD+∠ACD=140°-x°.
∵∠BG1C=(∠ABD+∠ACD)+∠A,∠BG1C=77°,
∴(140-x)+x=77,解得x=70.
∴∠A=70°.
28.(12分)(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于点D,CE⊥m于点E,求证:DE=BD+CE;
(2)拓展:如图2,将(1)中的条件改为在△ABC中,AB=AC,D,A,E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图3,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
图1 图2 图3
解:(1)证明:∵BD⊥m,CE⊥m,
∴∠BDA=∠AEC=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴AE=BD,AD=CE.
∴DE=AE+AD=BD+CE.
(2)结论DE=BD+CE成立.
证明:∵∠BDA=∠BAC=α,
∴∠ABD+∠BAD=∠BAD+∠CAE=180°-α.
∴∠CAE=∠ABD.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴AE=BD,AD=CE.
∴DE=AE+AD=BD+CE.
(3)∵∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,
∴∠CAE=∠ABD.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS).
∴S△ABD=S△CAE.
设△ABC的底边BC上的高为h,则△ACF的底边CF上的高为h,
则S△ABC=BC·h,S△ACF=CF·h.
∵BC=2CF,S△ABC=12,
∴S△ACF=S△ABC=6.
∵S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6,
∴△ABD与△CEF的面积之和为6.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
