18.1.2 平行四边形的判定 课件 (第一课时 50张)
文档属性
| 名称 | 18.1.2 平行四边形的判定 课件 (第一课时 50张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 394.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览





文档简介
18.1.2
平行四边形的判定
第1课时
18.1
平行四边形
一、温故知新,引入新课
1.平行四边形的定义是什么?
2.平行四边形的对边具有什么性质?写出这条性质定理.
3.它的逆命题是什么?你认为它成立吗?
1.两组对边分别平行的四边形是平行四边形.
2.平行四边形的两组对边分别相等.
逆命题:
两组对边分别相等的四边形是平行四边形.
这个命题是否成立?
二、猜想证明,探索新知
动手操作,实验探究:
每人拿出一条长20cm的线,想一想,能否将此线分成四段,然后首尾相连,构成一个平行四边形?
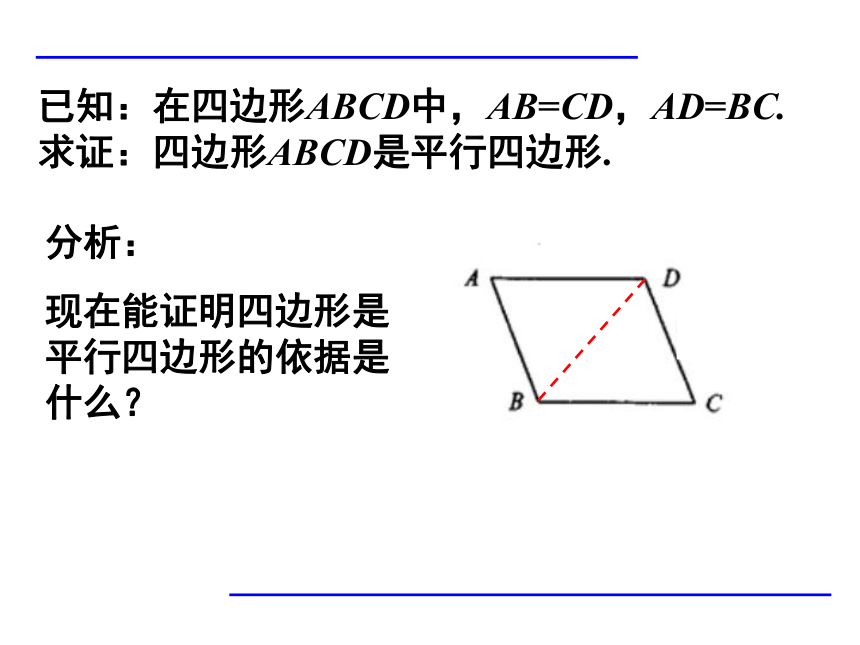
已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
分析:
现在能证明四边形是平行四边形的依据是什么?
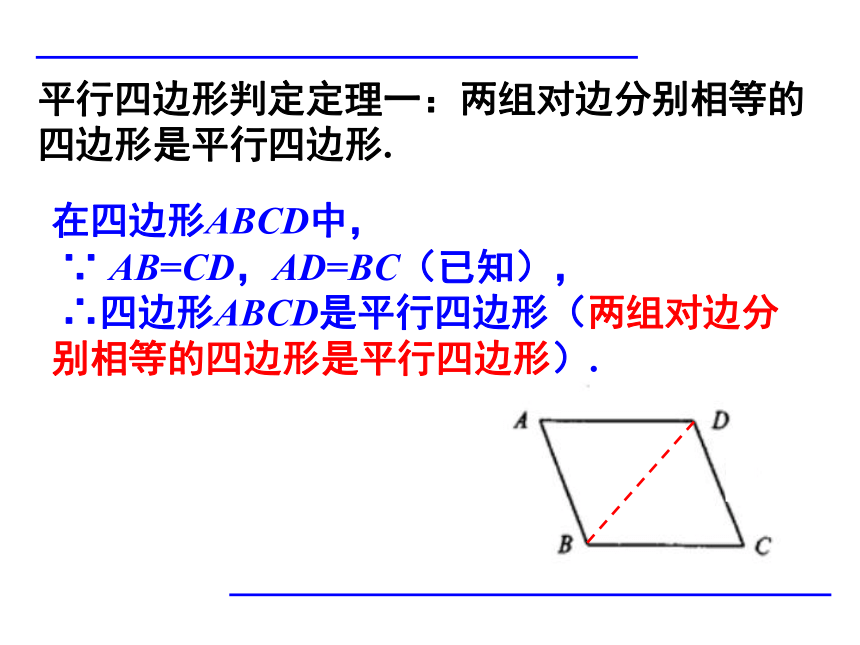
在四边形ABCD中,
∵
AB=CD,AD=BC(已知),
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
平行四边形判定定理一:两组对边分别相等的四边形是平行四边形.
探索其他判定方法:
你知道平行四边形还有哪些判定方法吗?说出这些命题,并尝试证明.
命题1:两组对角分别相等的四边形是平行四边形.
命题2:对角线互相平分的四边形是平行四边形.
请尝试用不同方法来证明.
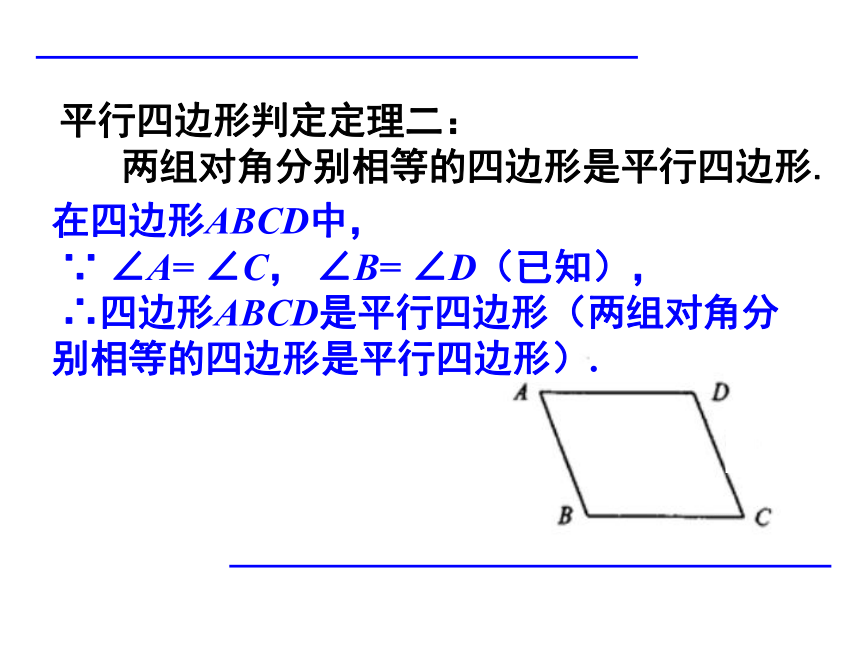
平行四边形判定定理二:
两组对角分别相等的四边形是平行四边形.
在四边形ABCD中,
∵
∠A=
∠C,
∠B=
∠D(已知),
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形).
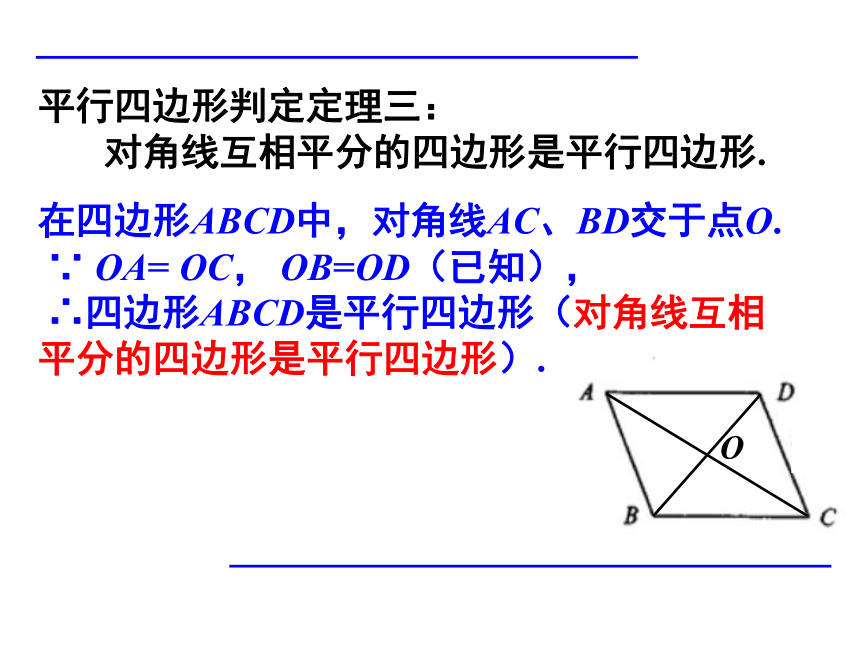
平行四边形判定定理三:
对角线互相平分的四边形是平行四边形.
在四边形ABCD中,对角线AC、BD交于点O.
∵
OA=
OC,
OB=OD(已知),
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).
O
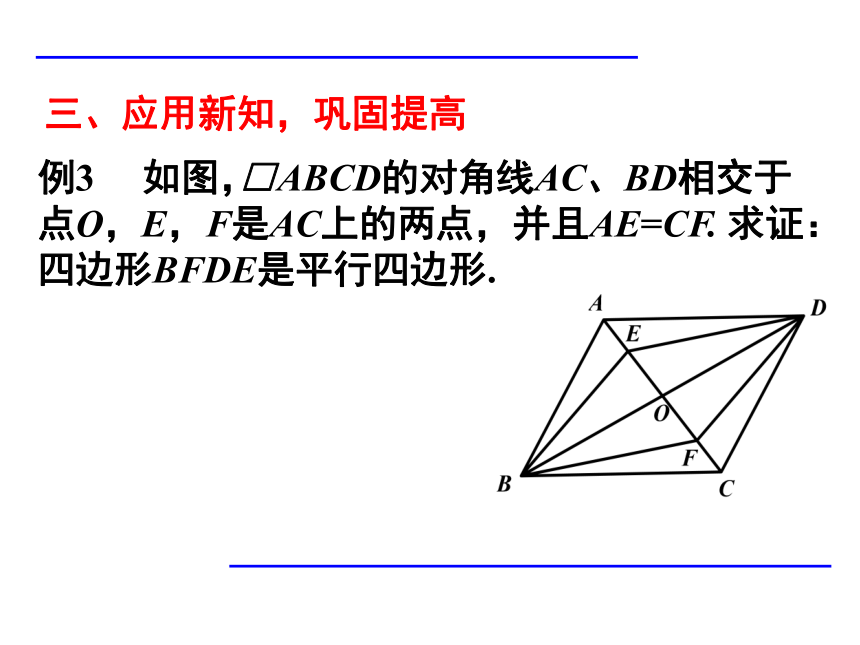
例3
如图,
ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
三、应用新知,巩固提高
□
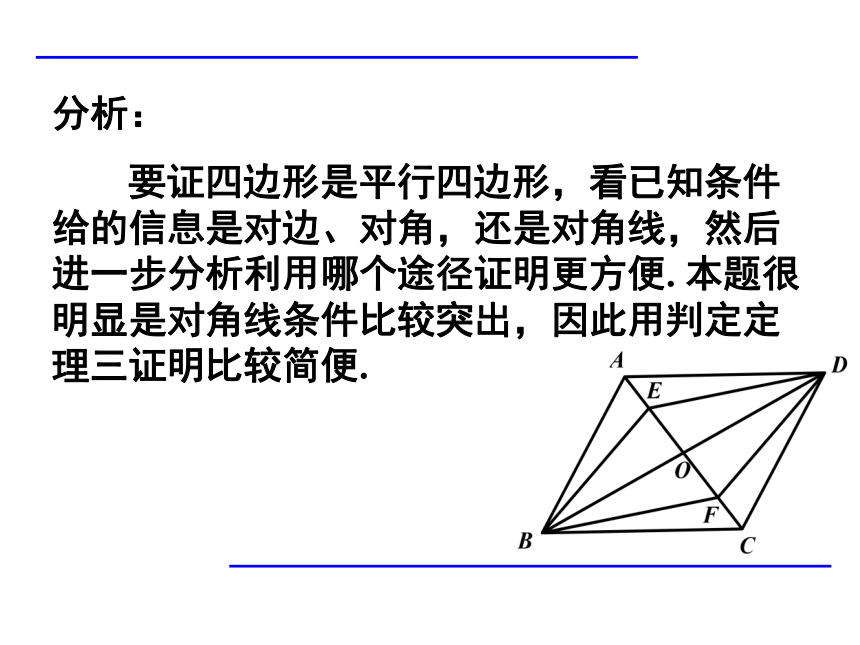
分析:
要证四边形是平行四边形,看已知条件给的信息是对边、对角,还是对角线,然后进一步分析利用哪个途径证明更方便.
本题很明显是对角线条件比较突出,因此用判定定理三证明比较简便.
提问:本题还有其他证法吗?
请从定义、几个判定定理分别考虑.
四、本课小结
本节课你学习了哪些知识?
获得了哪些研究问题的方法?
你有什么收获
?
知识上:
平行四边形的判定方法有定义、三个判定定理,分别从对边、对角和对角线来研究.
方法上:
将四边形转化为三角形是一般方法,体现了转化思想;
平行四边形的性质和判定定理是互逆命题,今后研究其他图形会类比这个研究方法进行;
先从简单问题入手研究,再扩展到其他问题,由简单到复杂.
18.1.2
平行四边形的判定
第2课时
18.1
平行四边形
一、温故知新,引入新课
1.回忆平行四边形的判定定理:
平形四边形的判定
两组对边分别平行的四边形是平行四边形
边
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
角
对角线
2.思考问题,引入新课.
思考
以小组讨论的形式探讨这一问题.
我们知道两组对边分别平行或相等的四边形是平行四边形.
请同学们猜想一下,如果只考虑四边形的一组对边,当它满足什么条件时这个四边形是平行四边形?
问题1:一组对边平行的四边形是平行四边形吗?如果是请给出证明,如果不是请举出反例说明.
二、猜想证明,探索新知
小学学习过的梯形满足一组对边平行的条件,但梯形不是平行四边形.
二、猜想证明,探索新知
问题2:满足一组对边相等的四边形是平行四边形吗?
如图1
,这个四边形EFGH满足一组对边EF=HG相等的条件,但它不是平行四边形.
二、猜想证明,探索新知
问题3:如果一组对边平行,而另一组对边相等的四边形是平行四边形吗?
如图2,等腰梯形属于一组对边平行(上底和下底),而另一组对边相等(两腰),但是等腰梯形不是平行四边形.
图2
二、猜想证明,探索新知
我们在方格纸上利用手中的木棍,做一个满足一组对边平行且相等的四边形,并判断所做的四边形是否是平行四边形.
请你猜想,这个命题成立吗?
命题:一组对边平行且相等的四边形是平行四边形.
命题:一组对边平行且相等的四边形是平行四边形.
请你将上述命题改写成已知、求证,并画出图形,然后思考如何证明.
图3
已知:如图3
,在四边
形ABCD中,AB//CD,
AB=CD.
求证:四边形ABCD是
平行四边形.
已知:如图,在四边形ABCD中,AB//CD,
AB=CD,
求证:四边形ABCD是平行四边形.
证明:方法1:如图,
连接
AC.
∵AB
//CD
,
∴∠1=∠2.
又
∵AB
=CD
,
AC
=CA
,
∴△ABC≌△CDA.
∴BC
=DA
.
∴四边形ABCD是平行四边形.
方法2:
∵AB
//CD
,
∴∠1=∠2
.
又
∵AB
=CD
,
AC
=CA
,
∴△ABC≌△CDA
.
∴∠BCA=∠DAC
.
∴AD
//BC
.
∴四边形ABCD是平行四边形.
如图,连接
AC.
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB
=CD,
∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
三、学以致用
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?
贴上图片
证明:
∵四边形ABCD是平行四边形,
∴AB
=CD,EB
//FD.
又
∵EB
=
AB
,FD
=
CD,
∴EB
=FD
.
∴四边形EBFD是平行四边形.
例
如图
,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
三、学以致用
2.
已知:如图,在四边形
ABCD中,对角线AC和BD相交于O,AO=OC,BA⊥AC,DC⊥AC.
求证:四边形ABCD是平行四边形.
四、应用新知,巩固提高
1.教材第47页练习第4题.
1.本节课你学习了哪些知识?
2.你获得了哪些研究问题的方法?
3.你有什么收获?
本课小结
两组对边分别平行的四边形是平行四边形
平形四边形的判定
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
18.1.2
平行四边形的判定
第3课时
18.1
平行四边形
温故知新
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
探究思考
请同学们按要求画图:
画任意△ABC中,画AB、AC边中点D、E,
连接DE.
D
E
定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
探究思考
问题1:
一个三角形有几条中位线?
D
E
F
三条
问题2:
三角形中位线与三角形中线有什么区别?
D
E
D
端点不同
探究思考
问题3:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
问题4:
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
探究思考
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
问题5:如何证明你的猜想?
探究思考
已知,如图,D、E分别是△ABC的边AB、
AC的中点.
求证:DE∥BC,
.
D
E
探究思考
平行
角
平行四边形
或
线段相等
一条线段是另一条线段的一半
倍长短线
分析1:
D
E
探究思考
分析2:
D
E
互相平分
构造
平行四边形
倍长DE
探究思考
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC
.
∵AE=EC,DE=EF
,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形.
证法1:
∴CF
AD
.
∴CF
BD
.
探究思考
证明:
D
E
∴
DE∥BC,
.
F
又
,
∴DF
BC
.
D
E
探究思考
证明:
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE,
(下面证明同证法1)
证法2:
,AD
CF.
∴BD
CF.
探究思考
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE=
BC.
三角形中位线定理:
符号语言:
探究思考
D
E
三角形的中位线
平行
一条线段是另一条线段的2倍或
三角形中位线定理:
学以致用
1.
如图,△ABC中,D、E分别是AB、AC中点.
(1)
若DE=5,则BC=
.
(2)
若∠B=65°,则∠ADE=
°.
(3)
若DE+BC=12,则BC=
.
10
65
x
2x
x+2x=12
x=4
8
学以致用
2.
如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么?
分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
N
M
根据是三角形中位线定理.
学以致用
例:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
连接对角线
三角形问题
(三角形中位线定理)
归纳小结
知识方面:三角形中位线概念;
三角形中位线定理.
思想方法方面:转化思想.
布置作业
必做题:教材第49页练习第1、2题.
选做题:再顺次连接本节课例题中所得到的四边形EFGH各边中点,又得到一个新的四边形,判断这个新四边形是否是平行四边形,并说明理由.
平行四边形的判定
第1课时
18.1
平行四边形
一、温故知新,引入新课
1.平行四边形的定义是什么?
2.平行四边形的对边具有什么性质?写出这条性质定理.
3.它的逆命题是什么?你认为它成立吗?
1.两组对边分别平行的四边形是平行四边形.
2.平行四边形的两组对边分别相等.
逆命题:
两组对边分别相等的四边形是平行四边形.
这个命题是否成立?
二、猜想证明,探索新知
动手操作,实验探究:
每人拿出一条长20cm的线,想一想,能否将此线分成四段,然后首尾相连,构成一个平行四边形?
已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
分析:
现在能证明四边形是平行四边形的依据是什么?
在四边形ABCD中,
∵
AB=CD,AD=BC(已知),
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
平行四边形判定定理一:两组对边分别相等的四边形是平行四边形.
探索其他判定方法:
你知道平行四边形还有哪些判定方法吗?说出这些命题,并尝试证明.
命题1:两组对角分别相等的四边形是平行四边形.
命题2:对角线互相平分的四边形是平行四边形.
请尝试用不同方法来证明.
平行四边形判定定理二:
两组对角分别相等的四边形是平行四边形.
在四边形ABCD中,
∵
∠A=
∠C,
∠B=
∠D(已知),
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形).
平行四边形判定定理三:
对角线互相平分的四边形是平行四边形.
在四边形ABCD中,对角线AC、BD交于点O.
∵
OA=
OC,
OB=OD(已知),
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).
O
例3
如图,
ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
三、应用新知,巩固提高
□
分析:
要证四边形是平行四边形,看已知条件给的信息是对边、对角,还是对角线,然后进一步分析利用哪个途径证明更方便.
本题很明显是对角线条件比较突出,因此用判定定理三证明比较简便.
提问:本题还有其他证法吗?
请从定义、几个判定定理分别考虑.
四、本课小结
本节课你学习了哪些知识?
获得了哪些研究问题的方法?
你有什么收获
?
知识上:
平行四边形的判定方法有定义、三个判定定理,分别从对边、对角和对角线来研究.
方法上:
将四边形转化为三角形是一般方法,体现了转化思想;
平行四边形的性质和判定定理是互逆命题,今后研究其他图形会类比这个研究方法进行;
先从简单问题入手研究,再扩展到其他问题,由简单到复杂.
18.1.2
平行四边形的判定
第2课时
18.1
平行四边形
一、温故知新,引入新课
1.回忆平行四边形的判定定理:
平形四边形的判定
两组对边分别平行的四边形是平行四边形
边
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
角
对角线
2.思考问题,引入新课.
思考
以小组讨论的形式探讨这一问题.
我们知道两组对边分别平行或相等的四边形是平行四边形.
请同学们猜想一下,如果只考虑四边形的一组对边,当它满足什么条件时这个四边形是平行四边形?
问题1:一组对边平行的四边形是平行四边形吗?如果是请给出证明,如果不是请举出反例说明.
二、猜想证明,探索新知
小学学习过的梯形满足一组对边平行的条件,但梯形不是平行四边形.
二、猜想证明,探索新知
问题2:满足一组对边相等的四边形是平行四边形吗?
如图1
,这个四边形EFGH满足一组对边EF=HG相等的条件,但它不是平行四边形.
二、猜想证明,探索新知
问题3:如果一组对边平行,而另一组对边相等的四边形是平行四边形吗?
如图2,等腰梯形属于一组对边平行(上底和下底),而另一组对边相等(两腰),但是等腰梯形不是平行四边形.
图2
二、猜想证明,探索新知
我们在方格纸上利用手中的木棍,做一个满足一组对边平行且相等的四边形,并判断所做的四边形是否是平行四边形.
请你猜想,这个命题成立吗?
命题:一组对边平行且相等的四边形是平行四边形.
命题:一组对边平行且相等的四边形是平行四边形.
请你将上述命题改写成已知、求证,并画出图形,然后思考如何证明.
图3
已知:如图3
,在四边
形ABCD中,AB//CD,
AB=CD.
求证:四边形ABCD是
平行四边形.
已知:如图,在四边形ABCD中,AB//CD,
AB=CD,
求证:四边形ABCD是平行四边形.
证明:方法1:如图,
连接
AC.
∵AB
//CD
,
∴∠1=∠2.
又
∵AB
=CD
,
AC
=CA
,
∴△ABC≌△CDA.
∴BC
=DA
.
∴四边形ABCD是平行四边形.
方法2:
∵AB
//CD
,
∴∠1=∠2
.
又
∵AB
=CD
,
AC
=CA
,
∴△ABC≌△CDA
.
∴∠BCA=∠DAC
.
∴AD
//BC
.
∴四边形ABCD是平行四边形.
如图,连接
AC.
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB
=CD,
∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
三、学以致用
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?
贴上图片
证明:
∵四边形ABCD是平行四边形,
∴AB
=CD,EB
//FD.
又
∵EB
=
AB
,FD
=
CD,
∴EB
=FD
.
∴四边形EBFD是平行四边形.
例
如图
,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
三、学以致用
2.
已知:如图,在四边形
ABCD中,对角线AC和BD相交于O,AO=OC,BA⊥AC,DC⊥AC.
求证:四边形ABCD是平行四边形.
四、应用新知,巩固提高
1.教材第47页练习第4题.
1.本节课你学习了哪些知识?
2.你获得了哪些研究问题的方法?
3.你有什么收获?
本课小结
两组对边分别平行的四边形是平行四边形
平形四边形的判定
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
18.1.2
平行四边形的判定
第3课时
18.1
平行四边形
温故知新
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
探究思考
请同学们按要求画图:
画任意△ABC中,画AB、AC边中点D、E,
连接DE.
D
E
定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
探究思考
问题1:
一个三角形有几条中位线?
D
E
F
三条
问题2:
三角形中位线与三角形中线有什么区别?
D
E
D
端点不同
探究思考
问题3:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
问题4:
绿色圃中小学教育网http://www.Lspjy.com
绿色圃中学资源网http://cz.Lspjy.com
探究思考
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
问题5:如何证明你的猜想?
探究思考
已知,如图,D、E分别是△ABC的边AB、
AC的中点.
求证:DE∥BC,
.
D
E
探究思考
平行
角
平行四边形
或
线段相等
一条线段是另一条线段的一半
倍长短线
分析1:
D
E
探究思考
分析2:
D
E
互相平分
构造
平行四边形
倍长DE
探究思考
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC
.
∵AE=EC,DE=EF
,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形.
证法1:
∴CF
AD
.
∴CF
BD
.
探究思考
证明:
D
E
∴
DE∥BC,
.
F
又
,
∴DF
BC
.
D
E
探究思考
证明:
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE,
(下面证明同证法1)
证法2:
,AD
CF.
∴BD
CF.
探究思考
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE=
BC.
三角形中位线定理:
符号语言:
探究思考
D
E
三角形的中位线
平行
一条线段是另一条线段的2倍或
三角形中位线定理:
学以致用
1.
如图,△ABC中,D、E分别是AB、AC中点.
(1)
若DE=5,则BC=
.
(2)
若∠B=65°,则∠ADE=
°.
(3)
若DE+BC=12,则BC=
.
10
65
x
2x
x+2x=12
x=4
8
学以致用
2.
如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么?
分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
N
M
根据是三角形中位线定理.
学以致用
例:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
连接对角线
三角形问题
(三角形中位线定理)
归纳小结
知识方面:三角形中位线概念;
三角形中位线定理.
思想方法方面:转化思想.
布置作业
必做题:教材第49页练习第1、2题.
选做题:再顺次连接本节课例题中所得到的四边形EFGH各边中点,又得到一个新的四边形,判断这个新四边形是否是平行四边形,并说明理由.
