山西省晋中市2020-2021学年九年级下学期开学数学试卷(Word版 含解析)
文档属性
| 名称 | 山西省晋中市2020-2021学年九年级下学期开学数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 633.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览


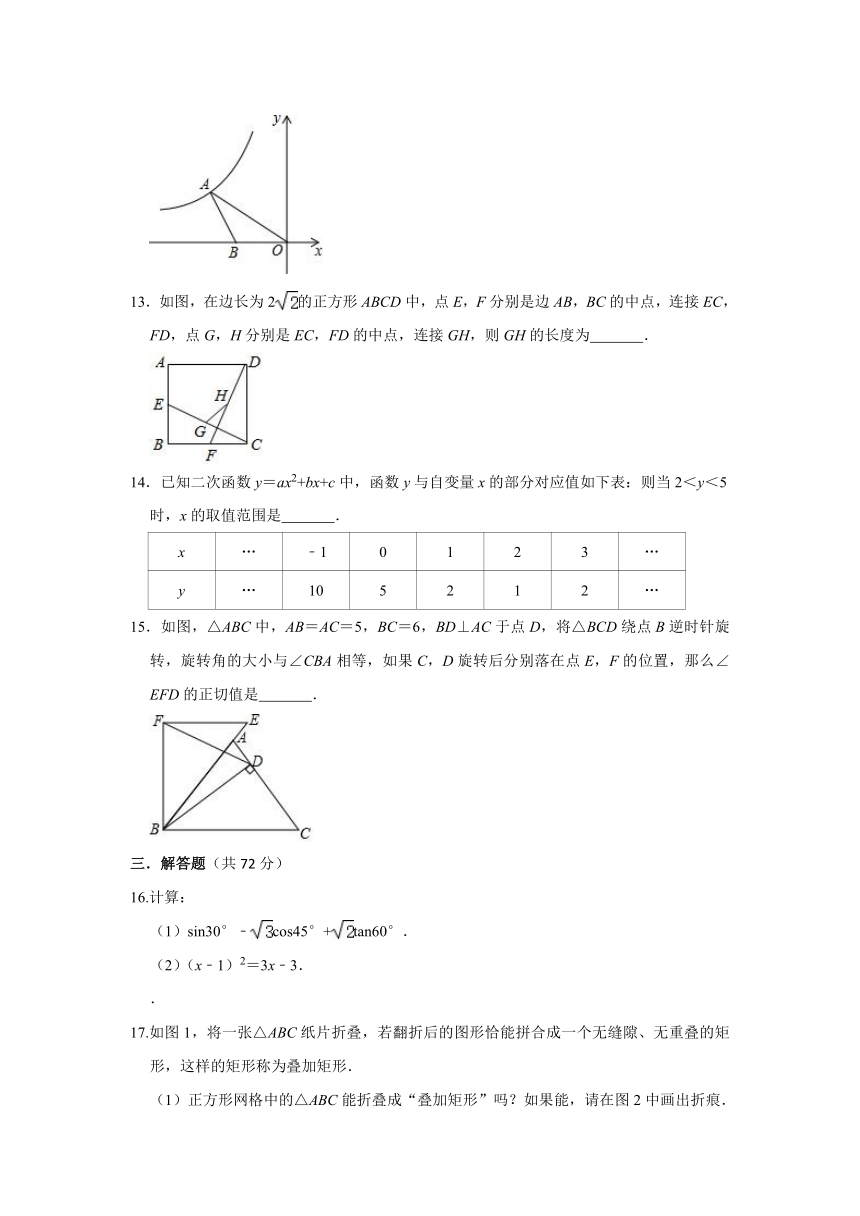
文档简介
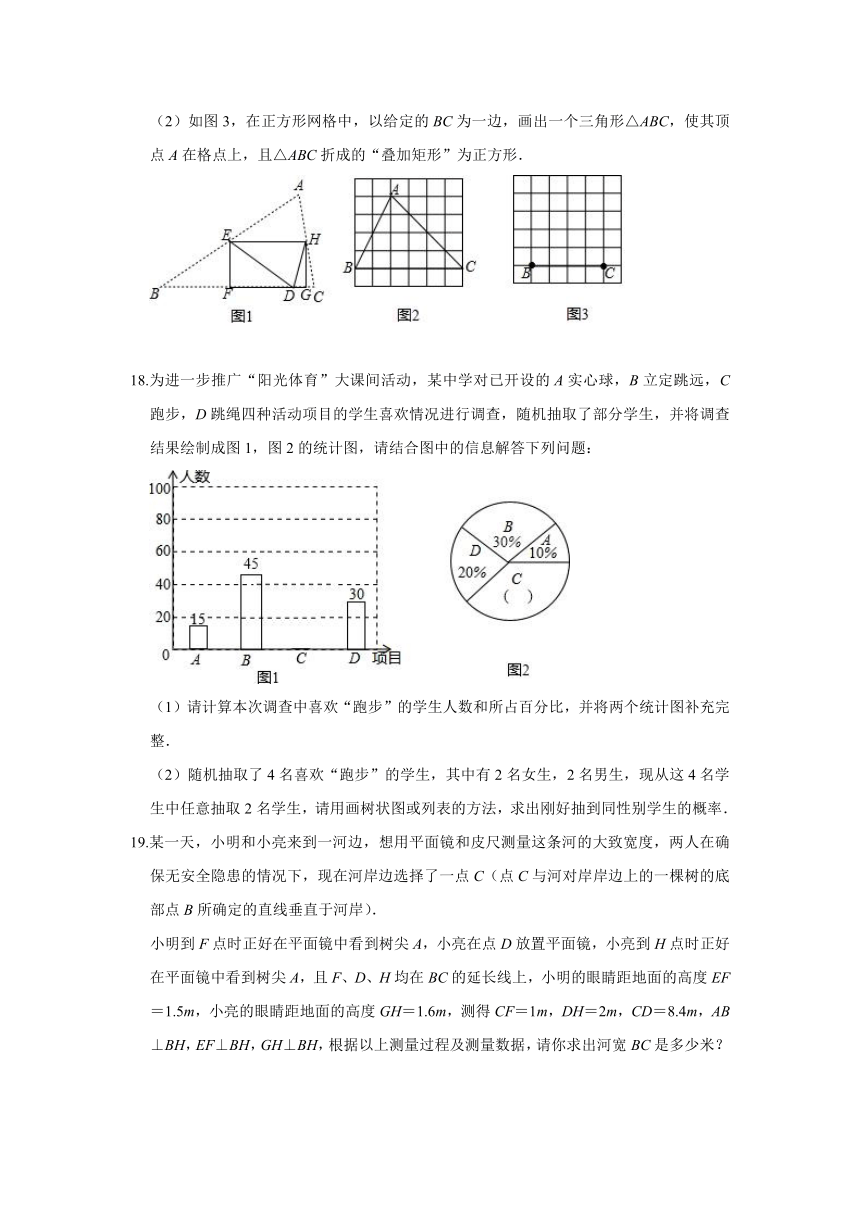
2020-2021学年山西省晋中市九年级(下)开学数学试卷
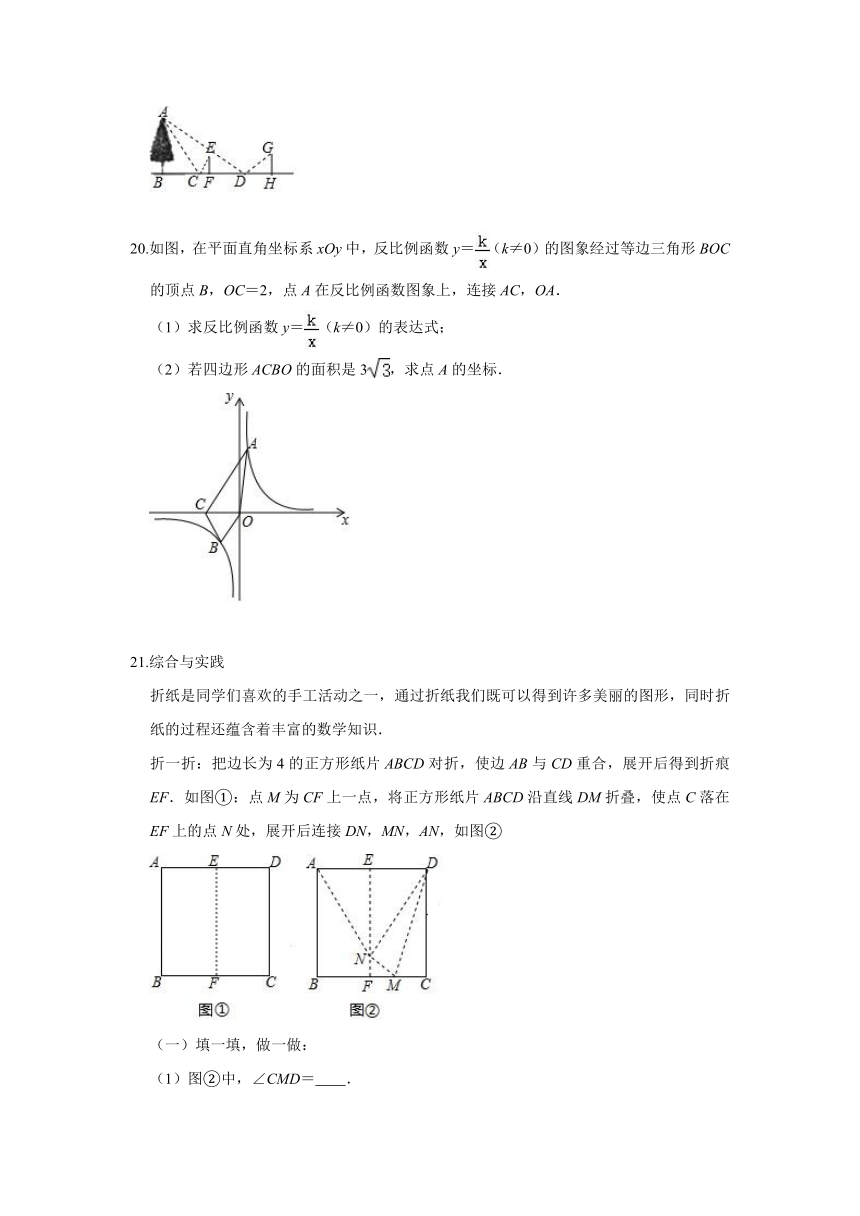
一.选择题(每小题3分,共30分)
1.对式子2a2﹣4a﹣1进行配方变形,正确的是( )
A.2(a+1)2﹣3
B.(a﹣1)2﹣
C.2(a﹣1)2﹣1
D.2(a﹣1)2﹣3
2.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A.矩形
B.菱形
C.对角线相等的四边形
D.对角线互相垂直的四边形
3.不透明的袋子里装有2个红球和1个白球,这些球除了颜色外都相同.从中任意摸一个,放回摇匀,再从中摸一个,则两次摸到球的颜色相同的概率是( )
A.
B.
C.
D.
4.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(﹣2,0)
C.(2,10)或(﹣2,0)
D.(10,2)或(﹣2,0)
5.已知反比例函数的图象经过点(﹣2,4),当x>2时,所对应的函数值y的取值范围是( )
A.﹣2<y<0
B.﹣3<y<﹣1
C.﹣4<y<0
D.0<y<1
6.将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为( )
A.y=(x+1)2﹣13
B.y=(x﹣5)2﹣3
C.y=(x﹣5)2﹣13
D.y=(x+1)2﹣3
7.如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
A.
B.
C.
D.
8.若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45°
B.45°<α<60°
C.60°<α<90°
D.30°<α<60°
9.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4
B.1:5
C.1:6
D.1:7
10.已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是( )
A.m=﹣1
B.m=3
C.m≤﹣1
D.m≥﹣1
二.填空题(
共18分)
11.观察表格,一元二次方程x2﹣x﹣1.1=0最精确的一个近似解是
(精确到0.1).
x
1.3
1.4
1.5
1.6
1.7
1.8
1.9
x2﹣x﹣1.1
﹣0.71
﹣0.54
﹣0.35
﹣0.14
0.09
0.34
0.61
12.如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=(x<0)的图象经过点A,若S△ABO=,则k的值为
.
13.如图,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为
.
14.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:则当2<y<5时,x的取值范围是
.
x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…
15.如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果C,D旋转后分别落在点E,F的位置,那么∠EFD的正切值是
.
三.解答题(共72分)
16.计算:
(1)sin30°﹣cos45°+tan60°.
(2)(x﹣1)2=3x﹣3.
.
17.如图1,将一张△ABC纸片折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠加矩形.
(1)正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕.
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个三角形△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形.
18.为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整.
(2)随机抽取了4名喜欢“跑步”的学生,其中有2名女生,2名男生,现从这4名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
19.某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸).
小明到F点时正好在平面镜中看到树尖A,小亮在点D放置平面镜,小亮到H点时正好在平面镜中看到树尖A,且F、D、H均在BC的延长线上,小明的眼睛距地面的高度EF=1.5m,小亮的眼睛距地面的高度GH=1.6m,测得CF=1m,DH=2m,CD=8.4m,AB⊥BH,EF⊥BH,GH⊥BH,根据以上测量过程及测量数据,请你求出河宽BC是多少米?
20.如图,在平面直角坐标系xOy中,反比例函数y=(k≠0)的图象经过等边三角形BOC的顶点B,OC=2,点A在反比例函数图象上,连接AC,OA.
(1)求反比例函数y=(k≠0)的表达式;
(2)若四边形ACBO的面积是3,求点A的坐标.
21.综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF.如图①:点M为CF上一点,将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,展开后连接DN,MN,AN,如图②
(一)填一填,做一做:
(1)图②中,∠CMD= .
线段NF=
(2)图②中,试判断△AND的形状,并给出证明.
剪一剪、折一折:将图②中的△AND剪下来,将其沿直线GH折叠,使点A落在点A′处,分别得到图③、图④.
(二)填一填
(3)图③中阴影部分的周长为 .
(4)图③中,若∠A′GN=80°,则∠A′HD= °.
(5)图③中的相似三角形(包括全等三角形)共有 对;
(6)如图④点A′落在边ND上,若=,则= (用含m,n的代数式表示).
22.在平面直角坐标系中,抛物线y=ax2+bx﹣3过点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D.
(1)求抛物线的解析式;
(2)点P为直线CD上的一个动点,连接BC;
①如图1,是否存在点P,使∠PBC=∠BCO?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由;
②如图2,点P在x轴上方,连接PA交抛物线于点N,∠PAB=∠BCO,点M在第三象限抛物线上,连接MN,当∠ANM=45°时,请直接写出点M的坐标.
参考答案与试题解析
一.选择题(共10小题)
1.对式子2a2﹣4a﹣1进行配方变形,正确的是( )
A.2(a+1)2﹣3
B.(a﹣1)2﹣
C.2(a﹣1)2﹣1
D.2(a﹣1)2﹣3
【分析】利用完全平方公式进行变形即可.
【解答】解:2a2﹣4a﹣1,
=2(a2﹣2a+1)﹣3,
=2(a﹣1)2﹣3.
故选:D.
2.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A.矩形
B.菱形
C.对角线相等的四边形
D.对角线互相垂直的四边形
【分析】首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.
【解答】已知:如右图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形ABCD是对角线垂直的四边形.
证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是矩形,即EF⊥FG,
∴AC⊥BD,
故选:D.
3.不透明的袋子里装有2个红球和1个白球,这些球除了颜色外都相同.从中任意摸一个,放回摇匀,再从中摸一个,则两次摸到球的颜色相同的概率是( )
A.
B.
C.
D.
【分析】列举出所有情况,看两次摸到球的情况占总情况的多少即可.
【解答】解:易得共有3×3=9种可能,两次摸到球的颜色相同的有5种,所以概率是.
故选:B.
4.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(﹣2,0)
C.(2,10)或(﹣2,0)
D.(10,2)或(﹣2,0)
【分析】分顺时针旋转和逆时针旋转两种情况讨论解答即可.
【解答】解:∵点D(5,3)在边AB上,
∴BC=5,BD=5﹣3=2,
①若顺时针旋转,则点D′在x轴上,OD′=2,
所以,D′(﹣2,0),
②若逆时针旋转,则点D′到x轴的距离为10,到y轴的距离为2,
所以,D′(2,10),
综上所述,点D′的坐标为(2,10)或(﹣2,0).
故选:C.
5.已知反比例函数的图象经过点(﹣2,4),当x>2时,所对应的函数值y的取值范围是( )
A.﹣2<y<0
B.﹣3<y<﹣1
C.﹣4<y<0
D.0<y<1
【分析】首先利用待定系数法可得反比例函数解析式,再画出反比例函数图象,求出当x=2时y的值,然后结合图象可得答案.
【解答】解:设反比例函数的关系式为y=,
∵图象经过点(﹣2,4),
∴k=﹣8,
∴y=﹣,
∴x=﹣,
当x=2时,y=﹣4,
结合图象可得当x>2时,﹣4<y<0,
故选:C.
6.将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为( )
A.y=(x+1)2﹣13
B.y=(x﹣5)2﹣3
C.y=(x﹣5)2﹣13
D.y=(x+1)2﹣3
【分析】先把一般式配成顶点式得到抛物线y=x2﹣4x﹣4的顶点坐标为(2,﹣8),再利用点平移的规律得到把点(2,﹣8)平移后所得对应点的坐标为(﹣1,﹣3),然后利用顶点式写出平移后的抛物线的函数表达式.
【解答】解:因为y=x2﹣4x﹣4=(x﹣2)2﹣8,
所以抛物线y=x2﹣4x﹣4的顶点坐标为(2,﹣8),把点(2,﹣8)向左平移3个单位,再向上平移5个单位所得对应点的坐标为(﹣1,﹣3),所以平移后的抛物线的函数表达式为y=(x+1)2﹣3.
故选:D.
7.如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
A.
B.
C.
D.
【分析】先判断出∠ADE=45°,进而判断出AE=AD,利用勾股定理即可得出结论.
【解答】
解:由折叠补全图形如图所示,
∵四边形ABCD是矩形,
∴∠ADA'=∠B=∠C=∠A=90°,AD=BC=1,CD=AB,
由第一次折叠得:∠DA'E=∠A=90°,∠ADE=∠ADC=45°,
∴∠AED=∠ADE=45°,
∴AE=AD=1,
在Rt△ADE中,根据勾股定理得,DE=AD=,
由第二次折叠知,CD=DE=,
∴AB=.
故选:A.
8.若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45°
B.45°<α<60°
C.60°<α<90°
D.30°<α<60°
【分析】先由特殊角的三角函数值及余弦函数随锐角的增大而减小,得出45°<α<90°;再由特殊角的三角函数值及正切函数随锐角的增大而增大,得出0<α<60°;从而得出45°<α<60°.
【解答】解:∵α是锐角,
∴cosα>0,
∵cosα<,
∴0<cosα<,
又∵cos90°=0,cos45°=,
∴45°<α<90°;
∵α是锐角,
∴tanα>0,
∵tanα<,
∴0<tanα<,
又∵tan0°=0,tan60°=,
0<α<60°;
故45°<α<60°.
故选:B.
9.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4
B.1:5
C.1:6
D.1:7
【分析】连接DE,连接并延长EP交BC于点F,利用DE是△ABC中位线,求出FC=BC,再用PQ是△EFC中位线,PQ=CF,即可求得答案.
【解答】解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,
,
∴△DEP≌△BFP(ASA),
∴BF=DE=BC,P是EF中点,
∴FC=BC,
PQ是△EFC中位线,
PQ=FC,
∴PQ:BC=1:4.
故选:A.
10.已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是( )
A.m=﹣1
B.m=3
C.m≤﹣1
D.m≥﹣1
【分析】根据二次函数的性质,利用二次函数的对称轴不大于1列式计算即可得解.
【解答】解:抛物线的对称轴为直线x=﹣,
∵当x>1时,y的值随x值的增大而增大,
由图象可知:﹣≤1,
解得m≥﹣1.
故选:D.
二.填空题(共5小题)
11.观察表格,一元二次方程x2﹣x﹣1.1=0最精确的一个近似解是 1.7 (精确到0.1).
x
1.3
1.4
1.5
1.6
1.7
1.8
1.9
x2﹣x﹣1.1
﹣0.71
﹣0.54
﹣0.35
﹣0.14
0.09
0.34
0.61
【分析】根据表格中的数据和题意可以解答本题.
【解答】解:由表格可知,
当x=1.7时,y=0.09与y=0最接近,
故答案为:1.7.
12.如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=(x<0)的图象经过点A,若S△ABO=,则k的值为 ﹣3 .
【分析】过点A作AD⊥x轴于点D,由∠AOB=30°可得出=,再根据BA=BO可得出∠ABD=60°,由此可得出=,根据线段间的关系即可得出线段OB、OD间的比例,结合反比例函数系数k的几何意义以及S△ABO=即可得出结论.
【解答】解:过点A作AD⊥x轴于点D,如图所示.
∵∠AOB=30°,AD⊥OD,
∴=cot∠AOB=,
∵∠AOB=30°,AB=BO,
∴∠AOB=∠BAO=30°,
∴∠ABD=60°,
∴=cot∠ABD=,
∵OB=OD﹣BD,
∴=,
∴=,
∵S△ABO=,
∴S△ADO=|k|=,
∵反比例函数图象在第二象限,
∴k=﹣3
故答案为:﹣3.
13.如图,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 1 .
【分析】方法一:连接CH并延长交AD于P,连接PE,根据正方形的性质得到∠A=90°,AD∥BC,AB=AD=BC=2,根据全等三角形的性质得到PD=CF=,根据勾股定理和三角形的中位线定理即可得到结论.
方法二:设DF,CE交于O,根据正方形的性质得到∠B=∠DCF=90°,BC=CD=AB,根据线段中点的定义得到BE=CF,根据全等三角形的性质得到CE=DF,∠BCE=∠CDF,求得DF⊥CE,根据勾股定理得到CE=DF==,点G,H分别是EC,PC的中点,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:方法一:连接CH并延长交AD于P,连接PE,
∵四边形ABCD是正方形,
∴∠A=90°,AD∥BC,AB=AD=BC=2,
∵E,F分别是边AB,BC的中点,
∴AE=CF=×2=,
∵AD∥BC,
∴∠DPH=∠FCH,
∵∠DHP=∠FHC,
∵DH=FH,
∴△PDH≌△CFH(AAS),
∴PD=CF=,
∴AP=AD﹣PD=,
∴PE===2,
∵点G,H分别是EC,CP的中点,
∴GH=EP=1;
方法二:设DF,CE交于O,
∵四边形ABCD是正方形,
∴∠B=∠DCF=90°,BC=CD=AB,
∵点E,F分别是边AB,BC的中点,
∴BE=CF,
∴△CBE≌△DCF(SAS),
∴CE=DF,∠BCE=∠CDF,
∵∠CDF+∠CFD=90°,
∴∠BCE+∠CFD=90°,
∴∠COF=90°,
∴DF⊥CE,
∴CE=DF==,
∵点G,H分别是EC,PC的中点,
∴CG=FH=,
∵∠DCF=90°,CO⊥DF,
∴∠DCO+∠FCO=∠DCO+∠CDO=90°,
∴∠FCO=∠CDO,
∵∠DCF=∠COF=90°,
∴△COF∽△DOC,
∴=,
∴CF2=OF?DF,
∴OF===,
∴OH=,OD=,
∵∠COF=∠COD=90°,
∴△COF∽△DOC,
∴,
∴OC2=OF?OD,
∴OC==,
∴OG=CG﹣OC=﹣=,
∴HG===1,
故答案为:1.
14.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:则当2<y<5时,x的取值范围是 0<x<1或3<x<4 .
x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…
【分析】根据二次函数的对称性及已知数据可知该二次函数的对称轴为x=2,结合表格中所给数据可得出答案.
【解答】解:
由所给数据可知当x=2时,y有最小值1,
∴二次函数的对称轴为x=2,
又由表格数据可知当2<y<5时,对应的x的范围为0<x<1,
又由二次函数的对称性可知当3<x<4时,y值的范围也是2<y<5,
故答案为:0<x<1或3<x<4.
15.如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果C,D旋转后分别落在点E,F的位置,那么∠EFD的正切值是 .
【分析】作AH⊥BC于H,延长CD交EF于G,根据等腰三角形的性质和勾股定理求出AH、BD、CD、AD,根据旋转变换的性质得到∠FBD=∠CBA,证明FB∥AH,根据四点共圆得到∠EFD=∠GBD,求出tan∠GBD即可.
【解答】解:作AH⊥BC于H,延长CD交EF于G,
∵AB=AC,
∴BH=CH=BC=3,
由勾股定理得,AH==4,
×BC×AH=×AC×BD,即6×4=5×BD,
解得,BD=,
∴CD==,AD=,
∵∠FBD=∠CBA,
∴∠FBE=∠DBC,
∵∠DBC+∠C=90°,∠HAC+∠C=90°,
∴∠FBE=∠BAH,
∴FB∥AH,
∴∠FBC=∠AHC=90°,
∴EF∥BC,
∴∠E=∠ABC=∠C=∠EGA,
∴AG=AE=BE﹣AB=BC﹣AB=1,
∴DG=,
∴∠F=∠BDC=90°,
∴F、B、D、G四点共圆,
∴∠EFD=∠GBD,
∴tan∠GBD==,
∴∠EFD的正切值是,
故答案为:.
三.解答题
16.计算:
(1)sin30°﹣cos45°+tan60°.
(2)(x﹣1)2=3x﹣3.
【考点】实数的运算;解一元二次方程﹣公式法;特殊角的三角函数值.版权所有
【专题】计算题;一元二次方程及应用;运算能力.
【答案】(1);
(2)x1=1,x2=4.
【分析】(1)根据特殊角的三角函数值进行实数的计算即可;
(2)运用因式分解法求解即可.
【解答】解:(1)原式=﹣×+×
=﹣+
=;
(2)(x﹣1)2=3x﹣3,
(x﹣1)2﹣3(x﹣1)=0,
(x﹣1)(x﹣1﹣3)=0,
解得,x1=1,x2=4.
17.如图1,将一张△ABC纸片折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠加矩形.
(1)正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕.
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个三角形△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形.
【考点】矩形的性质;作图—应用与设计作图;翻折变换(折叠问题).版权所有
【专题】作图题;几何直观.
【答案】(1)(2)作图见解析部分.
【分析】(1)根据要求画出图形即可.
(2)根据要求画出图形即可.
【解答】解:(1)如图2中,矩形EFGH即为所求作.
(2)如图3中,△ABC即为所求作.
18.为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整.
(2)随机抽取了4名喜欢“跑步”的学生,其中有2名女生,2名男生,现从这4名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
【考点】扇形统计图;条形统计图;列表法与树状图法.版权所有
【专题】概率及其应用;推理能力.
【答案】(1)60人,40%;
(2).
【分析】(1)用A的人数除以所占的百分比,即可求出调查的学生数,再用抽查的总人数减去A、B、D的人数,求出喜欢“跑步”的学生人数,再根据四个项目的百分比之和为1求出C对应的百分比,再补全统计图即可;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与刚好抽到同性别学生的情况,再利用概率公式即可求得答案.
【解答】解:(1)被调查的学生总人数为15÷10%=150(人),
本次调查中喜欢“跑步”的学生人数为150﹣(15+45+30)=60(人),所占百分比为1﹣(10%+30%+20%)=40%,
补全统计图如下:
(2)画树状图得:
∵共有12种等可能的结果,刚好抽到同性别学生的有4种情况,
∴刚好抽到同性别学生的概率为=.
19.某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸).
小明到F点时正好在平面镜中看到树尖A,小亮在点D放置平面镜,小亮到H点时正好在平面镜中看到树尖A,且F、D、H均在BC的延长线上,小明的眼睛距地面的高度EF=1.5m,小亮的眼睛距地面的高度GH=1.6m,测得CF=1m,DH=2m,CD=8.4m,AB⊥BH,EF⊥BH,GH⊥BH,根据以上测量过程及测量数据,请你求出河宽BC是多少米?
【考点】相似三角形的应用.版权所有
【答案】见试题解答内容
【分析】根据题意求出△ABC∽△EFC,△ABD∽△GHD,再根据相似三角形对应边成比例列式求解即可.
【解答】解:由题意可得:∠ACB=∠ECF,∠ADB=∠GDH.
∵AB⊥BH,EF⊥BH,GH⊥BH,
∴∠ABC=∠EFC=∠CHD=90°,
∴△ABC∽△EFC,
∴=,即=.
∵∠ADB=∠GDH,∠ABC=∠GHD=90°,
∴△ABD∽△GHD,
∴=,即=,
解得BC=9.6m.
答:河宽BC是9.6m.
20.如图,在平面直角坐标系xOy中,反比例函数y=(k≠0)的图象经过等边三角形BOC的顶点B,OC=2,点A在反比例函数图象上,连接AC,OA.
(1)求反比例函数y=(k≠0)的表达式;
(2)若四边形ACBO的面积是3,求点A的坐标.
【考点】反比例函数的性质;反比例函数系数k的几何意义;反比例函数图象上点的坐标特征;待定系数法求反比例函数解析式;等边三角形的性质.版权所有
【专题】反比例函数及其应用.
【答案】见试题解答内容
【分析】(1)作BD⊥OC于D,根据等边三角形的性质和勾股定理求得OD=1,BD=,进而求得三角形BOD的面积,根据系数k的几何意义即可求得k=,从而求得反比例函数的表达式;
(2)求得三角形AOC的面积,即可求得A的纵坐标,代入解析式求得横坐标,得出点A的坐标.
【解答】解:(1)作BD⊥OC于D,
∵△BOC是等边三角形,
∴OB=OC=2,OD=OC=1,
∴BD==,
∴S△OBD=OD×BD=,
S△OBD=|k|,
∴|k|=,
∵反比例函数y=(k≠0)的图象在一三象限,
∴k=,
∴反比例函数的表达式为y=;
(2)∵S△OBC=OC?BD==,
∴S△AOC=3﹣=2,
∵S△AOC=OC?yA=2,
∴yA=2,
把y=2代入y=,求得x=,
∴点A的坐标为(,2).
21.综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF.如图①:点M为CF上一点,将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,展开后连接DN,MN,AN,如图②
(一)填一填,做一做:
(1)图②中,∠CMD= .
线段NF=
(2)图②中,试判断△AND的形状,并给出证明.
剪一剪、折一折:将图②中的△AND剪下来,将其沿直线GH折叠,使点A落在点A′处,分别得到图③、图④.
(二)填一填
(3)图③中阴影部分的周长为 .
(4)图③中,若∠A′GN=80°,则∠A′HD= °.
(5)图③中的相似三角形(包括全等三角形)共有 对;
(6)如图④点A′落在边ND上,若=,则= (用含m,n的代数式表示).
【考点】相似形综合题.版权所有
【专题】几何综合题;图形的全等;等腰三角形与直角三角形;矩形
菱形
正方形;平移、旋转与对称;图形的相似.
【答案】见试题解答内容
【分析】(1)由折叠的性质得,四边形CDEF是矩形,得出EF=CD,∠DEF=90°,DE=AE=AD,由折叠的性质得出DN=CD=2DE,MN=CM,得出∠EDN=60°,得出∠CDM=∠NDM=15°,EN=DN=2,因此∠CMD=75°,NF=EF﹣EN=4﹣2;
(2)证明△AEN≌△DEN得出AN=DN,即可得出△AND是等边三角形;
(3)由折叠的性质得出A′G=AG,A′H=AH,得出图③中阴影部分的周长=△ADN的周长=12;
(4)由折叠的性质得出∠AGH=∠A′GH,∠AHG=∠A′HG,求出∠AGH=50°,得出∠AHG=∠A′HG=70°,即可得出结果;
(5)证明△NGM∽△A′NM∽△DNH,即可得出结论;
(6)设A'N=am,则A'D=an,证明△A′GH∽△HA′D,得出==,设A'G=AG=x,A'H=AH=y,则GN=4﹣x,DH=4﹣y,得出==,解得x=y,得出===.
【解答】解:(1)由折叠的性质得,四边形CDEF是矩形,
∴EF=CD,∠DEF=90°,DE=AE=AD,
∵将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,
∴DN=CD=2DE,MN=CM,
∴∠EDN=60°,
∴∠CDM=∠NDM=15°,EN=DN=2,
∴∠CMD=75°,NF=EF﹣EN=4﹣2;
故答案为:75°,4﹣2;
(2)△AND是等边三角形,理由如下:
在△AEN与△DEN中,,
∴△AEN≌△DEN(SAS),
∴AN=DN,
∵∠EDN=60°,
∴△AND是等边三角形;
(3)∵将图②中的△AND沿直线GH折叠,使点A落在点A′处,
∴A′G=AG,A′H=AH,
∴图③中阴影部分的周长=△ADN的周长=3×4=12;
故答案为:12;
(4)∵将图②中的△AND沿直线GH折叠,使点A落在点A′处,
∴∠AGH=∠A′GH,∠AHG=∠A′HG,
∵∠A′GN=80°,
∴∠AGH=50°,
∴∠AHG=∠A′HG=70°,
∴∠A′HD=180°﹣70°﹣70°=40°;
故答案为:40;
(5)如图③,
∵∠A=∠N=∠D=∠A′=60°,
∠NMG=∠A′MN,∠A′NM=∠DNH,
∴△NGM∽△A′NM∽△DNH,
∵△AGH≌△A′GH
∴图③中的相似三角形(包括全等三角形)共有4对,
故答案为:4;
(6)∵=,
设A'N=am,则A'D=an,
∵∠N=∠D=∠A=∠A′=60°,
∴∠NA′G+∠A′GN=∠NA′G+∠DA′H=120°,
∴∠A′GN=∠DA′H,
∴△A′GN∽△HA′D,
∴==,
设A'G=AG=x,A'H=AH=y,则GN=4﹣x,DH=4﹣y,
∴==,
解得:x=y,
∴===;
故答案为:.
22.在平面直角坐标系中,抛物线y=ax2+bx﹣3过点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D.
(1)求抛物线的解析式;
(2)点P为直线CD上的一个动点,连接BC;
①如图1,是否存在点P,使∠PBC=∠BCO?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由;
②如图2,点P在x轴上方,连接PA交抛物线于点N,∠PAB=∠BCO,点M在第三象限抛物线上,连接MN,当∠ANM=45°时,请直接写出点M的坐标.
【考点】二次函数综合题.版权所有
【专题】压轴题;数据分析观念.
【答案】见试题解答内容
【分析】(1)y=ax2+bx﹣3=a(x+3)(x﹣1),即可求解;
(2)①分点P(P′)在点C的右侧、点P在点C的左侧两种情况,分别求解即可;
②证明△AGR≌△RHM(AAS),则点M(m+n,n﹣m﹣3),利用点M在抛物线上和AR=NR,列出等式即可求解.
【解答】解:(1)y=ax2+bx﹣3=a(x+3)(x﹣1),
解得:a=1,
故抛物线的表达式为:y=x2+2x﹣3;
(2)由抛物线的表达式知,点C、D的坐标分别为(0,﹣3)、(﹣1,﹣4),
由点C、D的坐标知,直线CD的表达式为:y=x﹣3①;
tan∠BCO=,则cos∠BCO=;
①当点P(P′)在点C的右侧时,
∵∠P'BC=∠BCO,
故P′B∥y轴,则点P′(1,﹣2);
当点P在点C的左侧时,
设直线PB交y轴于点H,过点H作HN⊥BC于点N,
∵∠P'BC=∠BCO,
∴△BCH为等腰三角形,则BC=2CH?cos∠BCO=2×CH×=,
解得:CH=,则OH=3﹣CH=,故点H(0,﹣),
由点B、H的坐标得,直线BH的表达式为:y=x﹣②,
联立①②并解得:,
故点P的坐标为(﹣5,﹣8);
②∵∠PAB=∠BCO,而tan∠BCO=,
故设直线AP的表达式为:y=x+s,将点A的坐标代入上式并解得:s=1,
故直线AP的表达式为:y=x+1③,
联立①③并解得:,故点N(,);
设△AMN的外接圆为圆R,
当∠ANM=45°时,则∠ARM=90°,设圆心R的坐标为(m,n),
∵∠GRA+∠MRH=90°,∠MRH+∠RMH=90°,
∴∠RMH=∠GAR,
∵AR=MR,∠AGR=∠RHM=90°,
∴△AGR≌△RHM(AAS),
∴AG=m+3=RH,RG=﹣n=MH,
∴点M(m+n,n﹣m﹣3),
将点M的坐标代入抛物线表达式得:n﹣m﹣3=(m+n)2+2(m+n)﹣3④,
由题意得:AR=NR,即(m+3)2+n2=(m﹣)2+(﹣n)2⑤,
联立④⑤并解得:,
故点M(﹣,﹣).
一.选择题(每小题3分,共30分)
1.对式子2a2﹣4a﹣1进行配方变形,正确的是( )
A.2(a+1)2﹣3
B.(a﹣1)2﹣
C.2(a﹣1)2﹣1
D.2(a﹣1)2﹣3
2.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A.矩形
B.菱形
C.对角线相等的四边形
D.对角线互相垂直的四边形
3.不透明的袋子里装有2个红球和1个白球,这些球除了颜色外都相同.从中任意摸一个,放回摇匀,再从中摸一个,则两次摸到球的颜色相同的概率是( )
A.
B.
C.
D.
4.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(﹣2,0)
C.(2,10)或(﹣2,0)
D.(10,2)或(﹣2,0)
5.已知反比例函数的图象经过点(﹣2,4),当x>2时,所对应的函数值y的取值范围是( )
A.﹣2<y<0
B.﹣3<y<﹣1
C.﹣4<y<0
D.0<y<1
6.将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为( )
A.y=(x+1)2﹣13
B.y=(x﹣5)2﹣3
C.y=(x﹣5)2﹣13
D.y=(x+1)2﹣3
7.如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
A.
B.
C.
D.
8.若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45°
B.45°<α<60°
C.60°<α<90°
D.30°<α<60°
9.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4
B.1:5
C.1:6
D.1:7
10.已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是( )
A.m=﹣1
B.m=3
C.m≤﹣1
D.m≥﹣1
二.填空题(
共18分)
11.观察表格,一元二次方程x2﹣x﹣1.1=0最精确的一个近似解是
(精确到0.1).
x
1.3
1.4
1.5
1.6
1.7
1.8
1.9
x2﹣x﹣1.1
﹣0.71
﹣0.54
﹣0.35
﹣0.14
0.09
0.34
0.61
12.如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=(x<0)的图象经过点A,若S△ABO=,则k的值为
.
13.如图,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为
.
14.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:则当2<y<5时,x的取值范围是
.
x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…
15.如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果C,D旋转后分别落在点E,F的位置,那么∠EFD的正切值是
.
三.解答题(共72分)
16.计算:
(1)sin30°﹣cos45°+tan60°.
(2)(x﹣1)2=3x﹣3.
.
17.如图1,将一张△ABC纸片折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠加矩形.
(1)正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕.
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个三角形△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形.
18.为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整.
(2)随机抽取了4名喜欢“跑步”的学生,其中有2名女生,2名男生,现从这4名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
19.某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸).
小明到F点时正好在平面镜中看到树尖A,小亮在点D放置平面镜,小亮到H点时正好在平面镜中看到树尖A,且F、D、H均在BC的延长线上,小明的眼睛距地面的高度EF=1.5m,小亮的眼睛距地面的高度GH=1.6m,测得CF=1m,DH=2m,CD=8.4m,AB⊥BH,EF⊥BH,GH⊥BH,根据以上测量过程及测量数据,请你求出河宽BC是多少米?
20.如图,在平面直角坐标系xOy中,反比例函数y=(k≠0)的图象经过等边三角形BOC的顶点B,OC=2,点A在反比例函数图象上,连接AC,OA.
(1)求反比例函数y=(k≠0)的表达式;
(2)若四边形ACBO的面积是3,求点A的坐标.
21.综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF.如图①:点M为CF上一点,将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,展开后连接DN,MN,AN,如图②
(一)填一填,做一做:
(1)图②中,∠CMD= .
线段NF=
(2)图②中,试判断△AND的形状,并给出证明.
剪一剪、折一折:将图②中的△AND剪下来,将其沿直线GH折叠,使点A落在点A′处,分别得到图③、图④.
(二)填一填
(3)图③中阴影部分的周长为 .
(4)图③中,若∠A′GN=80°,则∠A′HD= °.
(5)图③中的相似三角形(包括全等三角形)共有 对;
(6)如图④点A′落在边ND上,若=,则= (用含m,n的代数式表示).
22.在平面直角坐标系中,抛物线y=ax2+bx﹣3过点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D.
(1)求抛物线的解析式;
(2)点P为直线CD上的一个动点,连接BC;
①如图1,是否存在点P,使∠PBC=∠BCO?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由;
②如图2,点P在x轴上方,连接PA交抛物线于点N,∠PAB=∠BCO,点M在第三象限抛物线上,连接MN,当∠ANM=45°时,请直接写出点M的坐标.
参考答案与试题解析
一.选择题(共10小题)
1.对式子2a2﹣4a﹣1进行配方变形,正确的是( )
A.2(a+1)2﹣3
B.(a﹣1)2﹣
C.2(a﹣1)2﹣1
D.2(a﹣1)2﹣3
【分析】利用完全平方公式进行变形即可.
【解答】解:2a2﹣4a﹣1,
=2(a2﹣2a+1)﹣3,
=2(a﹣1)2﹣3.
故选:D.
2.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A.矩形
B.菱形
C.对角线相等的四边形
D.对角线互相垂直的四边形
【分析】首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.
【解答】已知:如右图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形ABCD是对角线垂直的四边形.
证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是矩形,即EF⊥FG,
∴AC⊥BD,
故选:D.
3.不透明的袋子里装有2个红球和1个白球,这些球除了颜色外都相同.从中任意摸一个,放回摇匀,再从中摸一个,则两次摸到球的颜色相同的概率是( )
A.
B.
C.
D.
【分析】列举出所有情况,看两次摸到球的情况占总情况的多少即可.
【解答】解:易得共有3×3=9种可能,两次摸到球的颜色相同的有5种,所以概率是.
故选:B.
4.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(﹣2,0)
C.(2,10)或(﹣2,0)
D.(10,2)或(﹣2,0)
【分析】分顺时针旋转和逆时针旋转两种情况讨论解答即可.
【解答】解:∵点D(5,3)在边AB上,
∴BC=5,BD=5﹣3=2,
①若顺时针旋转,则点D′在x轴上,OD′=2,
所以,D′(﹣2,0),
②若逆时针旋转,则点D′到x轴的距离为10,到y轴的距离为2,
所以,D′(2,10),
综上所述,点D′的坐标为(2,10)或(﹣2,0).
故选:C.
5.已知反比例函数的图象经过点(﹣2,4),当x>2时,所对应的函数值y的取值范围是( )
A.﹣2<y<0
B.﹣3<y<﹣1
C.﹣4<y<0
D.0<y<1
【分析】首先利用待定系数法可得反比例函数解析式,再画出反比例函数图象,求出当x=2时y的值,然后结合图象可得答案.
【解答】解:设反比例函数的关系式为y=,
∵图象经过点(﹣2,4),
∴k=﹣8,
∴y=﹣,
∴x=﹣,
当x=2时,y=﹣4,
结合图象可得当x>2时,﹣4<y<0,
故选:C.
6.将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为( )
A.y=(x+1)2﹣13
B.y=(x﹣5)2﹣3
C.y=(x﹣5)2﹣13
D.y=(x+1)2﹣3
【分析】先把一般式配成顶点式得到抛物线y=x2﹣4x﹣4的顶点坐标为(2,﹣8),再利用点平移的规律得到把点(2,﹣8)平移后所得对应点的坐标为(﹣1,﹣3),然后利用顶点式写出平移后的抛物线的函数表达式.
【解答】解:因为y=x2﹣4x﹣4=(x﹣2)2﹣8,
所以抛物线y=x2﹣4x﹣4的顶点坐标为(2,﹣8),把点(2,﹣8)向左平移3个单位,再向上平移5个单位所得对应点的坐标为(﹣1,﹣3),所以平移后的抛物线的函数表达式为y=(x+1)2﹣3.
故选:D.
7.如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
A.
B.
C.
D.
【分析】先判断出∠ADE=45°,进而判断出AE=AD,利用勾股定理即可得出结论.
【解答】
解:由折叠补全图形如图所示,
∵四边形ABCD是矩形,
∴∠ADA'=∠B=∠C=∠A=90°,AD=BC=1,CD=AB,
由第一次折叠得:∠DA'E=∠A=90°,∠ADE=∠ADC=45°,
∴∠AED=∠ADE=45°,
∴AE=AD=1,
在Rt△ADE中,根据勾股定理得,DE=AD=,
由第二次折叠知,CD=DE=,
∴AB=.
故选:A.
8.若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45°
B.45°<α<60°
C.60°<α<90°
D.30°<α<60°
【分析】先由特殊角的三角函数值及余弦函数随锐角的增大而减小,得出45°<α<90°;再由特殊角的三角函数值及正切函数随锐角的增大而增大,得出0<α<60°;从而得出45°<α<60°.
【解答】解:∵α是锐角,
∴cosα>0,
∵cosα<,
∴0<cosα<,
又∵cos90°=0,cos45°=,
∴45°<α<90°;
∵α是锐角,
∴tanα>0,
∵tanα<,
∴0<tanα<,
又∵tan0°=0,tan60°=,
0<α<60°;
故45°<α<60°.
故选:B.
9.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4
B.1:5
C.1:6
D.1:7
【分析】连接DE,连接并延长EP交BC于点F,利用DE是△ABC中位线,求出FC=BC,再用PQ是△EFC中位线,PQ=CF,即可求得答案.
【解答】解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,
,
∴△DEP≌△BFP(ASA),
∴BF=DE=BC,P是EF中点,
∴FC=BC,
PQ是△EFC中位线,
PQ=FC,
∴PQ:BC=1:4.
故选:A.
10.已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是( )
A.m=﹣1
B.m=3
C.m≤﹣1
D.m≥﹣1
【分析】根据二次函数的性质,利用二次函数的对称轴不大于1列式计算即可得解.
【解答】解:抛物线的对称轴为直线x=﹣,
∵当x>1时,y的值随x值的增大而增大,
由图象可知:﹣≤1,
解得m≥﹣1.
故选:D.
二.填空题(共5小题)
11.观察表格,一元二次方程x2﹣x﹣1.1=0最精确的一个近似解是 1.7 (精确到0.1).
x
1.3
1.4
1.5
1.6
1.7
1.8
1.9
x2﹣x﹣1.1
﹣0.71
﹣0.54
﹣0.35
﹣0.14
0.09
0.34
0.61
【分析】根据表格中的数据和题意可以解答本题.
【解答】解:由表格可知,
当x=1.7时,y=0.09与y=0最接近,
故答案为:1.7.
12.如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=(x<0)的图象经过点A,若S△ABO=,则k的值为 ﹣3 .
【分析】过点A作AD⊥x轴于点D,由∠AOB=30°可得出=,再根据BA=BO可得出∠ABD=60°,由此可得出=,根据线段间的关系即可得出线段OB、OD间的比例,结合反比例函数系数k的几何意义以及S△ABO=即可得出结论.
【解答】解:过点A作AD⊥x轴于点D,如图所示.
∵∠AOB=30°,AD⊥OD,
∴=cot∠AOB=,
∵∠AOB=30°,AB=BO,
∴∠AOB=∠BAO=30°,
∴∠ABD=60°,
∴=cot∠ABD=,
∵OB=OD﹣BD,
∴=,
∴=,
∵S△ABO=,
∴S△ADO=|k|=,
∵反比例函数图象在第二象限,
∴k=﹣3
故答案为:﹣3.
13.如图,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 1 .
【分析】方法一:连接CH并延长交AD于P,连接PE,根据正方形的性质得到∠A=90°,AD∥BC,AB=AD=BC=2,根据全等三角形的性质得到PD=CF=,根据勾股定理和三角形的中位线定理即可得到结论.
方法二:设DF,CE交于O,根据正方形的性质得到∠B=∠DCF=90°,BC=CD=AB,根据线段中点的定义得到BE=CF,根据全等三角形的性质得到CE=DF,∠BCE=∠CDF,求得DF⊥CE,根据勾股定理得到CE=DF==,点G,H分别是EC,PC的中点,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:方法一:连接CH并延长交AD于P,连接PE,
∵四边形ABCD是正方形,
∴∠A=90°,AD∥BC,AB=AD=BC=2,
∵E,F分别是边AB,BC的中点,
∴AE=CF=×2=,
∵AD∥BC,
∴∠DPH=∠FCH,
∵∠DHP=∠FHC,
∵DH=FH,
∴△PDH≌△CFH(AAS),
∴PD=CF=,
∴AP=AD﹣PD=,
∴PE===2,
∵点G,H分别是EC,CP的中点,
∴GH=EP=1;
方法二:设DF,CE交于O,
∵四边形ABCD是正方形,
∴∠B=∠DCF=90°,BC=CD=AB,
∵点E,F分别是边AB,BC的中点,
∴BE=CF,
∴△CBE≌△DCF(SAS),
∴CE=DF,∠BCE=∠CDF,
∵∠CDF+∠CFD=90°,
∴∠BCE+∠CFD=90°,
∴∠COF=90°,
∴DF⊥CE,
∴CE=DF==,
∵点G,H分别是EC,PC的中点,
∴CG=FH=,
∵∠DCF=90°,CO⊥DF,
∴∠DCO+∠FCO=∠DCO+∠CDO=90°,
∴∠FCO=∠CDO,
∵∠DCF=∠COF=90°,
∴△COF∽△DOC,
∴=,
∴CF2=OF?DF,
∴OF===,
∴OH=,OD=,
∵∠COF=∠COD=90°,
∴△COF∽△DOC,
∴,
∴OC2=OF?OD,
∴OC==,
∴OG=CG﹣OC=﹣=,
∴HG===1,
故答案为:1.
14.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:则当2<y<5时,x的取值范围是 0<x<1或3<x<4 .
x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…
【分析】根据二次函数的对称性及已知数据可知该二次函数的对称轴为x=2,结合表格中所给数据可得出答案.
【解答】解:
由所给数据可知当x=2时,y有最小值1,
∴二次函数的对称轴为x=2,
又由表格数据可知当2<y<5时,对应的x的范围为0<x<1,
又由二次函数的对称性可知当3<x<4时,y值的范围也是2<y<5,
故答案为:0<x<1或3<x<4.
15.如图,△ABC中,AB=AC=5,BC=6,BD⊥AC于点D,将△BCD绕点B逆时针旋转,旋转角的大小与∠CBA相等,如果C,D旋转后分别落在点E,F的位置,那么∠EFD的正切值是 .
【分析】作AH⊥BC于H,延长CD交EF于G,根据等腰三角形的性质和勾股定理求出AH、BD、CD、AD,根据旋转变换的性质得到∠FBD=∠CBA,证明FB∥AH,根据四点共圆得到∠EFD=∠GBD,求出tan∠GBD即可.
【解答】解:作AH⊥BC于H,延长CD交EF于G,
∵AB=AC,
∴BH=CH=BC=3,
由勾股定理得,AH==4,
×BC×AH=×AC×BD,即6×4=5×BD,
解得,BD=,
∴CD==,AD=,
∵∠FBD=∠CBA,
∴∠FBE=∠DBC,
∵∠DBC+∠C=90°,∠HAC+∠C=90°,
∴∠FBE=∠BAH,
∴FB∥AH,
∴∠FBC=∠AHC=90°,
∴EF∥BC,
∴∠E=∠ABC=∠C=∠EGA,
∴AG=AE=BE﹣AB=BC﹣AB=1,
∴DG=,
∴∠F=∠BDC=90°,
∴F、B、D、G四点共圆,
∴∠EFD=∠GBD,
∴tan∠GBD==,
∴∠EFD的正切值是,
故答案为:.
三.解答题
16.计算:
(1)sin30°﹣cos45°+tan60°.
(2)(x﹣1)2=3x﹣3.
【考点】实数的运算;解一元二次方程﹣公式法;特殊角的三角函数值.版权所有
【专题】计算题;一元二次方程及应用;运算能力.
【答案】(1);
(2)x1=1,x2=4.
【分析】(1)根据特殊角的三角函数值进行实数的计算即可;
(2)运用因式分解法求解即可.
【解答】解:(1)原式=﹣×+×
=﹣+
=;
(2)(x﹣1)2=3x﹣3,
(x﹣1)2﹣3(x﹣1)=0,
(x﹣1)(x﹣1﹣3)=0,
解得,x1=1,x2=4.
17.如图1,将一张△ABC纸片折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠加矩形.
(1)正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕.
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个三角形△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形.
【考点】矩形的性质;作图—应用与设计作图;翻折变换(折叠问题).版权所有
【专题】作图题;几何直观.
【答案】(1)(2)作图见解析部分.
【分析】(1)根据要求画出图形即可.
(2)根据要求画出图形即可.
【解答】解:(1)如图2中,矩形EFGH即为所求作.
(2)如图3中,△ABC即为所求作.
18.为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整.
(2)随机抽取了4名喜欢“跑步”的学生,其中有2名女生,2名男生,现从这4名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
【考点】扇形统计图;条形统计图;列表法与树状图法.版权所有
【专题】概率及其应用;推理能力.
【答案】(1)60人,40%;
(2).
【分析】(1)用A的人数除以所占的百分比,即可求出调查的学生数,再用抽查的总人数减去A、B、D的人数,求出喜欢“跑步”的学生人数,再根据四个项目的百分比之和为1求出C对应的百分比,再补全统计图即可;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与刚好抽到同性别学生的情况,再利用概率公式即可求得答案.
【解答】解:(1)被调查的学生总人数为15÷10%=150(人),
本次调查中喜欢“跑步”的学生人数为150﹣(15+45+30)=60(人),所占百分比为1﹣(10%+30%+20%)=40%,
补全统计图如下:
(2)画树状图得:
∵共有12种等可能的结果,刚好抽到同性别学生的有4种情况,
∴刚好抽到同性别学生的概率为=.
19.某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸).
小明到F点时正好在平面镜中看到树尖A,小亮在点D放置平面镜,小亮到H点时正好在平面镜中看到树尖A,且F、D、H均在BC的延长线上,小明的眼睛距地面的高度EF=1.5m,小亮的眼睛距地面的高度GH=1.6m,测得CF=1m,DH=2m,CD=8.4m,AB⊥BH,EF⊥BH,GH⊥BH,根据以上测量过程及测量数据,请你求出河宽BC是多少米?
【考点】相似三角形的应用.版权所有
【答案】见试题解答内容
【分析】根据题意求出△ABC∽△EFC,△ABD∽△GHD,再根据相似三角形对应边成比例列式求解即可.
【解答】解:由题意可得:∠ACB=∠ECF,∠ADB=∠GDH.
∵AB⊥BH,EF⊥BH,GH⊥BH,
∴∠ABC=∠EFC=∠CHD=90°,
∴△ABC∽△EFC,
∴=,即=.
∵∠ADB=∠GDH,∠ABC=∠GHD=90°,
∴△ABD∽△GHD,
∴=,即=,
解得BC=9.6m.
答:河宽BC是9.6m.
20.如图,在平面直角坐标系xOy中,反比例函数y=(k≠0)的图象经过等边三角形BOC的顶点B,OC=2,点A在反比例函数图象上,连接AC,OA.
(1)求反比例函数y=(k≠0)的表达式;
(2)若四边形ACBO的面积是3,求点A的坐标.
【考点】反比例函数的性质;反比例函数系数k的几何意义;反比例函数图象上点的坐标特征;待定系数法求反比例函数解析式;等边三角形的性质.版权所有
【专题】反比例函数及其应用.
【答案】见试题解答内容
【分析】(1)作BD⊥OC于D,根据等边三角形的性质和勾股定理求得OD=1,BD=,进而求得三角形BOD的面积,根据系数k的几何意义即可求得k=,从而求得反比例函数的表达式;
(2)求得三角形AOC的面积,即可求得A的纵坐标,代入解析式求得横坐标,得出点A的坐标.
【解答】解:(1)作BD⊥OC于D,
∵△BOC是等边三角形,
∴OB=OC=2,OD=OC=1,
∴BD==,
∴S△OBD=OD×BD=,
S△OBD=|k|,
∴|k|=,
∵反比例函数y=(k≠0)的图象在一三象限,
∴k=,
∴反比例函数的表达式为y=;
(2)∵S△OBC=OC?BD==,
∴S△AOC=3﹣=2,
∵S△AOC=OC?yA=2,
∴yA=2,
把y=2代入y=,求得x=,
∴点A的坐标为(,2).
21.综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF.如图①:点M为CF上一点,将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,展开后连接DN,MN,AN,如图②
(一)填一填,做一做:
(1)图②中,∠CMD= .
线段NF=
(2)图②中,试判断△AND的形状,并给出证明.
剪一剪、折一折:将图②中的△AND剪下来,将其沿直线GH折叠,使点A落在点A′处,分别得到图③、图④.
(二)填一填
(3)图③中阴影部分的周长为 .
(4)图③中,若∠A′GN=80°,则∠A′HD= °.
(5)图③中的相似三角形(包括全等三角形)共有 对;
(6)如图④点A′落在边ND上,若=,则= (用含m,n的代数式表示).
【考点】相似形综合题.版权所有
【专题】几何综合题;图形的全等;等腰三角形与直角三角形;矩形
菱形
正方形;平移、旋转与对称;图形的相似.
【答案】见试题解答内容
【分析】(1)由折叠的性质得,四边形CDEF是矩形,得出EF=CD,∠DEF=90°,DE=AE=AD,由折叠的性质得出DN=CD=2DE,MN=CM,得出∠EDN=60°,得出∠CDM=∠NDM=15°,EN=DN=2,因此∠CMD=75°,NF=EF﹣EN=4﹣2;
(2)证明△AEN≌△DEN得出AN=DN,即可得出△AND是等边三角形;
(3)由折叠的性质得出A′G=AG,A′H=AH,得出图③中阴影部分的周长=△ADN的周长=12;
(4)由折叠的性质得出∠AGH=∠A′GH,∠AHG=∠A′HG,求出∠AGH=50°,得出∠AHG=∠A′HG=70°,即可得出结果;
(5)证明△NGM∽△A′NM∽△DNH,即可得出结论;
(6)设A'N=am,则A'D=an,证明△A′GH∽△HA′D,得出==,设A'G=AG=x,A'H=AH=y,则GN=4﹣x,DH=4﹣y,得出==,解得x=y,得出===.
【解答】解:(1)由折叠的性质得,四边形CDEF是矩形,
∴EF=CD,∠DEF=90°,DE=AE=AD,
∵将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,
∴DN=CD=2DE,MN=CM,
∴∠EDN=60°,
∴∠CDM=∠NDM=15°,EN=DN=2,
∴∠CMD=75°,NF=EF﹣EN=4﹣2;
故答案为:75°,4﹣2;
(2)△AND是等边三角形,理由如下:
在△AEN与△DEN中,,
∴△AEN≌△DEN(SAS),
∴AN=DN,
∵∠EDN=60°,
∴△AND是等边三角形;
(3)∵将图②中的△AND沿直线GH折叠,使点A落在点A′处,
∴A′G=AG,A′H=AH,
∴图③中阴影部分的周长=△ADN的周长=3×4=12;
故答案为:12;
(4)∵将图②中的△AND沿直线GH折叠,使点A落在点A′处,
∴∠AGH=∠A′GH,∠AHG=∠A′HG,
∵∠A′GN=80°,
∴∠AGH=50°,
∴∠AHG=∠A′HG=70°,
∴∠A′HD=180°﹣70°﹣70°=40°;
故答案为:40;
(5)如图③,
∵∠A=∠N=∠D=∠A′=60°,
∠NMG=∠A′MN,∠A′NM=∠DNH,
∴△NGM∽△A′NM∽△DNH,
∵△AGH≌△A′GH
∴图③中的相似三角形(包括全等三角形)共有4对,
故答案为:4;
(6)∵=,
设A'N=am,则A'D=an,
∵∠N=∠D=∠A=∠A′=60°,
∴∠NA′G+∠A′GN=∠NA′G+∠DA′H=120°,
∴∠A′GN=∠DA′H,
∴△A′GN∽△HA′D,
∴==,
设A'G=AG=x,A'H=AH=y,则GN=4﹣x,DH=4﹣y,
∴==,
解得:x=y,
∴===;
故答案为:.
22.在平面直角坐标系中,抛物线y=ax2+bx﹣3过点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D.
(1)求抛物线的解析式;
(2)点P为直线CD上的一个动点,连接BC;
①如图1,是否存在点P,使∠PBC=∠BCO?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由;
②如图2,点P在x轴上方,连接PA交抛物线于点N,∠PAB=∠BCO,点M在第三象限抛物线上,连接MN,当∠ANM=45°时,请直接写出点M的坐标.
【考点】二次函数综合题.版权所有
【专题】压轴题;数据分析观念.
【答案】见试题解答内容
【分析】(1)y=ax2+bx﹣3=a(x+3)(x﹣1),即可求解;
(2)①分点P(P′)在点C的右侧、点P在点C的左侧两种情况,分别求解即可;
②证明△AGR≌△RHM(AAS),则点M(m+n,n﹣m﹣3),利用点M在抛物线上和AR=NR,列出等式即可求解.
【解答】解:(1)y=ax2+bx﹣3=a(x+3)(x﹣1),
解得:a=1,
故抛物线的表达式为:y=x2+2x﹣3;
(2)由抛物线的表达式知,点C、D的坐标分别为(0,﹣3)、(﹣1,﹣4),
由点C、D的坐标知,直线CD的表达式为:y=x﹣3①;
tan∠BCO=,则cos∠BCO=;
①当点P(P′)在点C的右侧时,
∵∠P'BC=∠BCO,
故P′B∥y轴,则点P′(1,﹣2);
当点P在点C的左侧时,
设直线PB交y轴于点H,过点H作HN⊥BC于点N,
∵∠P'BC=∠BCO,
∴△BCH为等腰三角形,则BC=2CH?cos∠BCO=2×CH×=,
解得:CH=,则OH=3﹣CH=,故点H(0,﹣),
由点B、H的坐标得,直线BH的表达式为:y=x﹣②,
联立①②并解得:,
故点P的坐标为(﹣5,﹣8);
②∵∠PAB=∠BCO,而tan∠BCO=,
故设直线AP的表达式为:y=x+s,将点A的坐标代入上式并解得:s=1,
故直线AP的表达式为:y=x+1③,
联立①③并解得:,故点N(,);
设△AMN的外接圆为圆R,
当∠ANM=45°时,则∠ARM=90°,设圆心R的坐标为(m,n),
∵∠GRA+∠MRH=90°,∠MRH+∠RMH=90°,
∴∠RMH=∠GAR,
∵AR=MR,∠AGR=∠RHM=90°,
∴△AGR≌△RHM(AAS),
∴AG=m+3=RH,RG=﹣n=MH,
∴点M(m+n,n﹣m﹣3),
将点M的坐标代入抛物线表达式得:n﹣m﹣3=(m+n)2+2(m+n)﹣3④,
由题意得:AR=NR,即(m+3)2+n2=(m﹣)2+(﹣n)2⑤,
联立④⑤并解得:,
故点M(﹣,﹣).
同课章节目录
