2020-2021学年鲁教版(五四制)九年级下册数学 期末达标检测卷(word版含答案)
文档属性
| 名称 | 2020-2021学年鲁教版(五四制)九年级下册数学 期末达标检测卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 17:36:14 | ||
图片预览




文档简介
期末达标检测卷
一、选择题(每题3分,共30分)
1.下列结论正确的是( )
A.长度相等的两条弧是等弧
B.半圆是弧
C.相等的圆心角所对的弧相等
D.一条弦所对的所有的圆周角相等
2.如图,在半径为10的⊙O中,弦AB的长为16,则这条弦的弦心距为( )
A.
6
B.
8
C.
10
D.
12
3.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C作与边AB相切的动圆,与CB,CA分别相交于点E,F,则线段EF长度的最小值是( )
A.4
B.4.75
C.5
D.
4.8
4.如图,已知BC为⊙O的直径,AD⊥BC,垂足为D,=,
∠ABF=30°,则∠BAD等于( )
A.
30°
B.
45°
C.
60°
D.
22.5°
5.一个盒子中装有标号为1,2,3,4,5的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于5的概率为( )
A.
B.
C.
D.
6.已知圆的半径为6.5cm,圆心到直线l的距离为4.5cm,那么这条直线和这个圆的公共点的个数是( )
A.0
B.1
C.2
D.无法确定
7.在一次质检抽测中,随机抽取某摊位20袋食盐,测得各袋的质量分别为(单位:g):
492
496
494
495
498
497
501
502
504
496
497
503
506
508
507
492
496
500
501
499
根据以上抽测结果,估计任买一袋该摊位的食盐,质量在497.5
g~501.5
g之间的概率为( )
A.
B.
C.
D.
8.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
A.60°
B.90°
C.120°
D.180°
9.如图,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动地在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径与x轴围成的面积为( )
A.+
B.
+1
C.
π+1
D.
π+
10.如图,抛物线过点A(2,0),B(6,0),C,平行于x轴的直线CD交抛物线于点C,D,以AB为直径的圆交直线CD于点E,F,则CE+FD的值是( )
A.
2
B.
4
C.
3
D.
6
二、填空题(每题3分,共24分)
11.如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD.则以下结论:①=;②AD∥BC;③AE∶BE=1∶2;④△ADE∽△BCE.其中不一定成立的是________.(填序号)
12.如图,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC,BC分别相切于点D,E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则BG的长是________.
13.一个口袋中有4个黑球和若干个白球,在不允许将球倒出来数的前提下,要估算白球的个数,小明从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色……不断重复上述过程.他共摸了100次,其中20次摸到黑球,根据上述数据,小明可估计口袋中的白球有________个.
14.已知圆锥的侧面展开图的圆心角是180°,底面积为15
cm2,则圆锥的侧面积为________cm2.
15.如图,在菱形ABCD中,AB=1,∠BAD=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为,则图中阴影部分的面积为__________.
16.从半径为9
cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为________.
17.淘淘和丽丽是非常要好的九年级学生,在物理、化学、生物实验技能考试中,考试科目要求三选一,并且采取抽签方式取得,那么他们两人都抽到物理实验的概率是__________.
18.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中捕获30条鱼,在每条鱼身上做好记号后,把这些鱼放归鱼塘,再从鱼塘中打捞200条鱼.若在这200条鱼中有5条鱼是有记号的,则可估计鱼塘中有鱼________________条.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图,点A,B,C是⊙O上的三点,AB∥OC.
(1)求证:AC平分∠OAB;
(2)过点O作OE⊥AB于点E,交AC于点P.若AB=2,∠AOE=30°,求PE的长.
20.某射击运动员在同一条件下的射击成绩记录如下:
射击次数
10
20
30
40
50
60
80
100
射中8环以上的频数
6
17
25
31
39
49
65
80
射中8环以上的频率
(1)计算表中相应的频率;(精确到0.01)
(2)估计这名运动员射击一次时“射中8环以上”的概率.(精确到0.1)
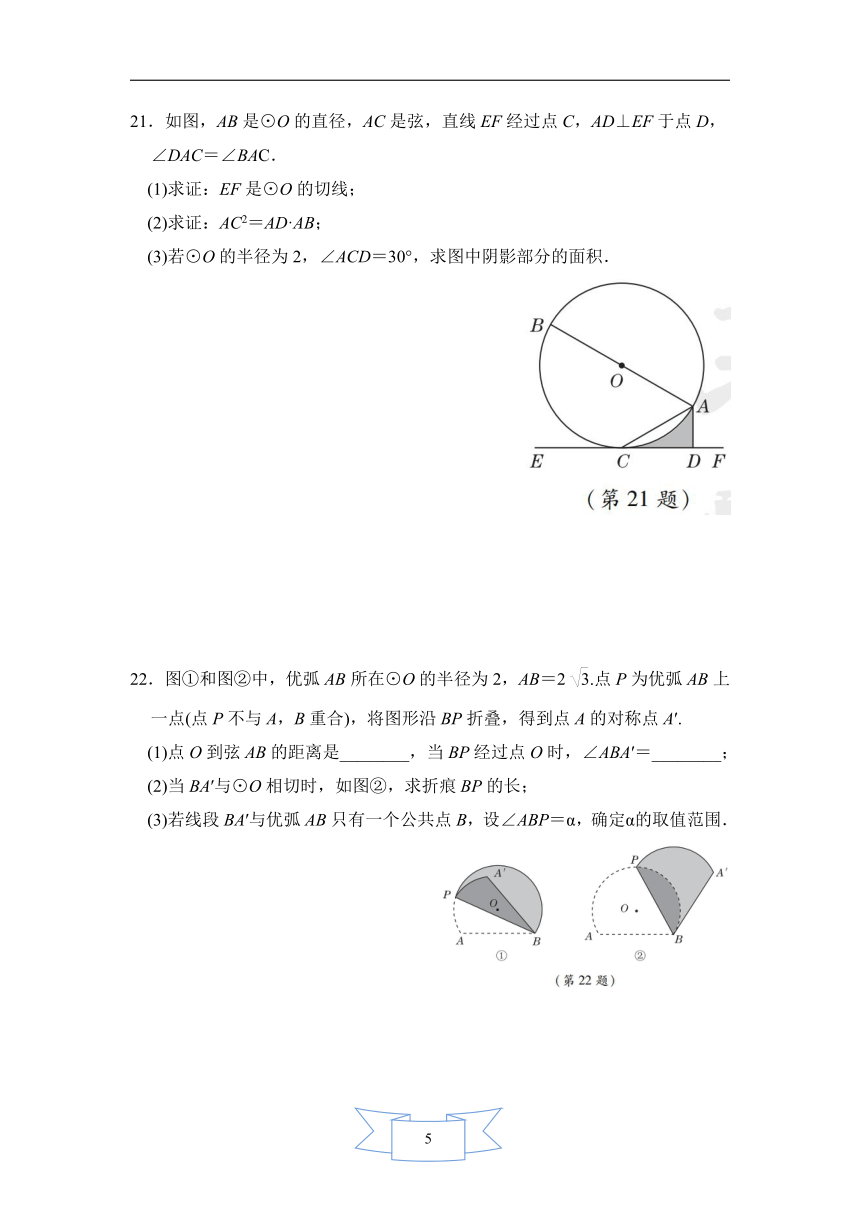
21.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
22.图①和图②中,优弧AB所在⊙O的半径为2,AB=2
.点P为优弧AB上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
(1)点O到弦AB的距离是________,当BP经过点O时,∠ABA′=________;
(2)当BA′与⊙O相切时,如图②,求折痕BP的长;
(3)若线段BA′与优弧AB只有一个公共点B,设∠ABP=α,确定α的取值范围.
23.小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下,小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和,若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率;
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
24.已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①所示),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②所示),设另一交点为E,连接AE,OC,若AE∥OC.
①AE与OD的大小有什么关系?为什么?
②求∠ODC
的度数.
答案
一、1.B 点拨:在同圆或等圆中,完全重合的弧才是等弧,长度相等的弧不一定是等弧,故A错误;半圆是弧,B正确;在同圆或等圆中,相等的圆心角所对的弧才相等,故C错误;弦为直径时所对的圆周角都相等,弦不是直径时,顶点在优弧与劣弧上的圆周角不相等,故D错误.
2.A 3.D 4.A 5.C 6.C 7.B 8.C
9.C 点拨:如图,点A运动的路径与x轴围成的面积为S1+S2+S3+S4+S5=+++2×
=π+1.故选C.
10.B 点拨:如图,∵点A,B的坐标分别是(2,0),(6,0),∴AB的中点M的坐标为(4,0),且点M是圆心,作MN⊥CD于点N,则EN=FN,又由抛物线的对称性可知CN=DN,∴CE=DF.连接EM.在Rt△EMN中,EN====1.
又CN=4-1=3,
∴CE=CN-EN=3-1=2,
∴CE+DF=2+2=4.
二、11.③ 12.2
-2 13.16 14.30
15.+- 点拨:如图,连接D′C,BC′,BD′,易知A,D′,C在同一直线上,A,B,C′在同一直线上.过D′作D′E⊥AB于E,过C作CH⊥AC′于H.由旋转可知,S阴影=S扇形CAC′-2S△D′FC.在Rt△AD′E中,∠D′AE=30°,AD′=1,∴D′E=,AE=.
在Rt△BD′E中,
BE=1-,
D′B2=2+2=2-.
可证∠D′FB=∠CFC′=90°,△D′BF是等腰直角三角形,∴D′F2=,
∴BF=D′F==,
∴CF=1-=.
在Rt△CBH中,∠CBH=60°,BC=1,
∴BH=,CH=.
∴AH=.∴AC2=3.
∴S△D′FC=×D′F×CF=××=,
S扇形CAC′=×AC2=×3=.
∴S阴影=S扇形CAC′-2×S△D′FC=-2×=+-.
16.3
cm 17. 18.1
200
三、19.(1)证明:∵AB∥OC,
∴∠C=∠BAC.
∵OA=OC,∴∠C=∠OAC.
∴∠BAC=∠OAC,
即AC平分∠OAB.
(2)解:∵OE⊥AB,
∴AE=BE=AB=1.
又∵∠AOE=30°,∠OEA=90°,
∴∠OAE=60°.
∴∠EAP=∠OAE=30°.
∵tan
∠EAP=,
∴PE=AE·tan
∠EAP=1×=.
∴PE的长是.
20.解:(1)表中的频率依次为0.60,0.85,0.83,0.78,0.78,0.82,0.81,0.80.
(2)可以看出:随着射击次数的增多,运动员射中8环以上的频率稳定在0.8左右,从而估计他射击一次时,“射中8环以上”的概率为0.8.
21.(1)证明:连接OC.
∵AD⊥EF,
∴∠ADC=90°.
∴∠ACD+∠CAD=90°.
∵OC=OA,∴∠ACO=∠CAO.
∵∠DAC=∠BAC,
∴∠ACD+∠ACO=90°,
即∠OCD=90°.
∴EF是⊙O的切线.
(2)证明:连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵AD⊥EF,
∴∠ADC=90°=∠ACB.
∵∠DAC=∠BAC,
∴△ACD∽△ABC.
∴=,即AC2=AB·AD.
(3)解:∵CD是⊙O的切线,
∴∠OCD=90°,
即∠ACD+∠ACO=90°.
∵∠ACD=30°,
∴∠OCA=60°.
∵OC=OA,
∴△ACO是等边三角形.
∴AC=OC=2,∠AOC=60°.
在Rt△ADC中,
∵∠ACD=30°,
∴AD=1,CD=.
∴S阴影=S梯形OCDA-S扇形OCA=(1+2)×-=-.
22.解:(1)1;60°
(2)作OC⊥AB于点C,连接OB,如图所示.
∵BA′与⊙O相切,
∴∠OBA′=90°.
在Rt△OBC中,OB=2,OC=1,
∴sin
∠OBC==.
∴∠OBC=30°.
∴∠ABP=∠ABA′=(∠OBA′+∠OBC)=60°.
∴∠OBP=30°.
作OD⊥BP于点D,则BP=2BD.
∵BD=OB·cos
30°=,
∴BP=2
.
(3)∵点P,A不重合,∴α>0°.
由(1)得,当α增大到30°时,点A′在优弧AB上,
∴当0°<α<30°时,点A′在⊙O内,线段BA′与优弧AB只有一个公共点B.
由(2)知,α增大到60°时,BA′与⊙O相切,即线段BA′与优弧AB只有一个公共点B.
当α继续增大时,点P逐渐靠近点B,但点P,B不重合,∴∠OBP<90°.∵α=∠OBA+∠OBP,∠OBA=30°,∴α<120°.∴当60°≤α<120°时,线段BA′与优弧AB只有一个公共点B.
综上所述,α的取值范围是0°<α<30°或60°≤α<120°.
23.解:(1)列表如下:
总共有9种结果,每种结果出现的可能性相同,而两数和为6的结果有3种,因此P(两数和为6)=.
(2)这个游戏规则对双方不公平.
理由:因为P(和为奇数)=,
P(和为偶数)=,而≠,
所以这个游戏规则对双方是不公平的.
24.解:(1)如图①所示,连接OC,
则∠OCD=90°.
∵OC=OA,CD=OA,
∴OC=CD.
∴∠ODC=∠COD.
∵∠ODC+∠COD=90°,
∴∠ODC=45°.
(2)如图②所示,连接OE.
∵CD=OA,
∴CD=OC=OE=OA.
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠1=x,
则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°-2x.
①AE=OD,理由如下:
在△AOE与△OCD中,
∴△AOE≌△OCD(SAS).
∴AE=OD.
②∵OE=OC,
∠6=∠1+∠2=2x,
∴∠5=∠6=2x,
∵AE∥OC,
∴∠4+∠5+∠6=180°,
即x+2x+2x=180°.
∴x=36°.
∴∠ODC=36°.
一、选择题(每题3分,共30分)
1.下列结论正确的是( )
A.长度相等的两条弧是等弧
B.半圆是弧
C.相等的圆心角所对的弧相等
D.一条弦所对的所有的圆周角相等
2.如图,在半径为10的⊙O中,弦AB的长为16,则这条弦的弦心距为( )
A.
6
B.
8
C.
10
D.
12
3.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C作与边AB相切的动圆,与CB,CA分别相交于点E,F,则线段EF长度的最小值是( )
A.4
B.4.75
C.5
D.
4.8
4.如图,已知BC为⊙O的直径,AD⊥BC,垂足为D,=,
∠ABF=30°,则∠BAD等于( )
A.
30°
B.
45°
C.
60°
D.
22.5°
5.一个盒子中装有标号为1,2,3,4,5的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于5的概率为( )
A.
B.
C.
D.
6.已知圆的半径为6.5cm,圆心到直线l的距离为4.5cm,那么这条直线和这个圆的公共点的个数是( )
A.0
B.1
C.2
D.无法确定
7.在一次质检抽测中,随机抽取某摊位20袋食盐,测得各袋的质量分别为(单位:g):
492
496
494
495
498
497
501
502
504
496
497
503
506
508
507
492
496
500
501
499
根据以上抽测结果,估计任买一袋该摊位的食盐,质量在497.5
g~501.5
g之间的概率为( )
A.
B.
C.
D.
8.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
A.60°
B.90°
C.120°
D.180°
9.如图,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动地在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径与x轴围成的面积为( )
A.+
B.
+1
C.
π+1
D.
π+
10.如图,抛物线过点A(2,0),B(6,0),C,平行于x轴的直线CD交抛物线于点C,D,以AB为直径的圆交直线CD于点E,F,则CE+FD的值是( )
A.
2
B.
4
C.
3
D.
6
二、填空题(每题3分,共24分)
11.如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD.则以下结论:①=;②AD∥BC;③AE∶BE=1∶2;④△ADE∽△BCE.其中不一定成立的是________.(填序号)
12.如图,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC,BC分别相切于点D,E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则BG的长是________.
13.一个口袋中有4个黑球和若干个白球,在不允许将球倒出来数的前提下,要估算白球的个数,小明从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色……不断重复上述过程.他共摸了100次,其中20次摸到黑球,根据上述数据,小明可估计口袋中的白球有________个.
14.已知圆锥的侧面展开图的圆心角是180°,底面积为15
cm2,则圆锥的侧面积为________cm2.
15.如图,在菱形ABCD中,AB=1,∠BAD=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为,则图中阴影部分的面积为__________.
16.从半径为9
cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为________.
17.淘淘和丽丽是非常要好的九年级学生,在物理、化学、生物实验技能考试中,考试科目要求三选一,并且采取抽签方式取得,那么他们两人都抽到物理实验的概率是__________.
18.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中捕获30条鱼,在每条鱼身上做好记号后,把这些鱼放归鱼塘,再从鱼塘中打捞200条鱼.若在这200条鱼中有5条鱼是有记号的,则可估计鱼塘中有鱼________________条.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图,点A,B,C是⊙O上的三点,AB∥OC.
(1)求证:AC平分∠OAB;
(2)过点O作OE⊥AB于点E,交AC于点P.若AB=2,∠AOE=30°,求PE的长.
20.某射击运动员在同一条件下的射击成绩记录如下:
射击次数
10
20
30
40
50
60
80
100
射中8环以上的频数
6
17
25
31
39
49
65
80
射中8环以上的频率
(1)计算表中相应的频率;(精确到0.01)
(2)估计这名运动员射击一次时“射中8环以上”的概率.(精确到0.1)
21.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
22.图①和图②中,优弧AB所在⊙O的半径为2,AB=2
.点P为优弧AB上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
(1)点O到弦AB的距离是________,当BP经过点O时,∠ABA′=________;
(2)当BA′与⊙O相切时,如图②,求折痕BP的长;
(3)若线段BA′与优弧AB只有一个公共点B,设∠ABP=α,确定α的取值范围.
23.小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下,小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和,若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率;
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
24.已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①所示),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②所示),设另一交点为E,连接AE,OC,若AE∥OC.
①AE与OD的大小有什么关系?为什么?
②求∠ODC
的度数.
答案
一、1.B 点拨:在同圆或等圆中,完全重合的弧才是等弧,长度相等的弧不一定是等弧,故A错误;半圆是弧,B正确;在同圆或等圆中,相等的圆心角所对的弧才相等,故C错误;弦为直径时所对的圆周角都相等,弦不是直径时,顶点在优弧与劣弧上的圆周角不相等,故D错误.
2.A 3.D 4.A 5.C 6.C 7.B 8.C
9.C 点拨:如图,点A运动的路径与x轴围成的面积为S1+S2+S3+S4+S5=+++2×
=π+1.故选C.
10.B 点拨:如图,∵点A,B的坐标分别是(2,0),(6,0),∴AB的中点M的坐标为(4,0),且点M是圆心,作MN⊥CD于点N,则EN=FN,又由抛物线的对称性可知CN=DN,∴CE=DF.连接EM.在Rt△EMN中,EN====1.
又CN=4-1=3,
∴CE=CN-EN=3-1=2,
∴CE+DF=2+2=4.
二、11.③ 12.2
-2 13.16 14.30
15.+- 点拨:如图,连接D′C,BC′,BD′,易知A,D′,C在同一直线上,A,B,C′在同一直线上.过D′作D′E⊥AB于E,过C作CH⊥AC′于H.由旋转可知,S阴影=S扇形CAC′-2S△D′FC.在Rt△AD′E中,∠D′AE=30°,AD′=1,∴D′E=,AE=.
在Rt△BD′E中,
BE=1-,
D′B2=2+2=2-.
可证∠D′FB=∠CFC′=90°,△D′BF是等腰直角三角形,∴D′F2=,
∴BF=D′F==,
∴CF=1-=.
在Rt△CBH中,∠CBH=60°,BC=1,
∴BH=,CH=.
∴AH=.∴AC2=3.
∴S△D′FC=×D′F×CF=××=,
S扇形CAC′=×AC2=×3=.
∴S阴影=S扇形CAC′-2×S△D′FC=-2×=+-.
16.3
cm 17. 18.1
200
三、19.(1)证明:∵AB∥OC,
∴∠C=∠BAC.
∵OA=OC,∴∠C=∠OAC.
∴∠BAC=∠OAC,
即AC平分∠OAB.
(2)解:∵OE⊥AB,
∴AE=BE=AB=1.
又∵∠AOE=30°,∠OEA=90°,
∴∠OAE=60°.
∴∠EAP=∠OAE=30°.
∵tan
∠EAP=,
∴PE=AE·tan
∠EAP=1×=.
∴PE的长是.
20.解:(1)表中的频率依次为0.60,0.85,0.83,0.78,0.78,0.82,0.81,0.80.
(2)可以看出:随着射击次数的增多,运动员射中8环以上的频率稳定在0.8左右,从而估计他射击一次时,“射中8环以上”的概率为0.8.
21.(1)证明:连接OC.
∵AD⊥EF,
∴∠ADC=90°.
∴∠ACD+∠CAD=90°.
∵OC=OA,∴∠ACO=∠CAO.
∵∠DAC=∠BAC,
∴∠ACD+∠ACO=90°,
即∠OCD=90°.
∴EF是⊙O的切线.
(2)证明:连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵AD⊥EF,
∴∠ADC=90°=∠ACB.
∵∠DAC=∠BAC,
∴△ACD∽△ABC.
∴=,即AC2=AB·AD.
(3)解:∵CD是⊙O的切线,
∴∠OCD=90°,
即∠ACD+∠ACO=90°.
∵∠ACD=30°,
∴∠OCA=60°.
∵OC=OA,
∴△ACO是等边三角形.
∴AC=OC=2,∠AOC=60°.
在Rt△ADC中,
∵∠ACD=30°,
∴AD=1,CD=.
∴S阴影=S梯形OCDA-S扇形OCA=(1+2)×-=-.
22.解:(1)1;60°
(2)作OC⊥AB于点C,连接OB,如图所示.
∵BA′与⊙O相切,
∴∠OBA′=90°.
在Rt△OBC中,OB=2,OC=1,
∴sin
∠OBC==.
∴∠OBC=30°.
∴∠ABP=∠ABA′=(∠OBA′+∠OBC)=60°.
∴∠OBP=30°.
作OD⊥BP于点D,则BP=2BD.
∵BD=OB·cos
30°=,
∴BP=2
.
(3)∵点P,A不重合,∴α>0°.
由(1)得,当α增大到30°时,点A′在优弧AB上,
∴当0°<α<30°时,点A′在⊙O内,线段BA′与优弧AB只有一个公共点B.
由(2)知,α增大到60°时,BA′与⊙O相切,即线段BA′与优弧AB只有一个公共点B.
当α继续增大时,点P逐渐靠近点B,但点P,B不重合,∴∠OBP<90°.∵α=∠OBA+∠OBP,∠OBA=30°,∴α<120°.∴当60°≤α<120°时,线段BA′与优弧AB只有一个公共点B.
综上所述,α的取值范围是0°<α<30°或60°≤α<120°.
23.解:(1)列表如下:
总共有9种结果,每种结果出现的可能性相同,而两数和为6的结果有3种,因此P(两数和为6)=.
(2)这个游戏规则对双方不公平.
理由:因为P(和为奇数)=,
P(和为偶数)=,而≠,
所以这个游戏规则对双方是不公平的.
24.解:(1)如图①所示,连接OC,
则∠OCD=90°.
∵OC=OA,CD=OA,
∴OC=CD.
∴∠ODC=∠COD.
∵∠ODC+∠COD=90°,
∴∠ODC=45°.
(2)如图②所示,连接OE.
∵CD=OA,
∴CD=OC=OE=OA.
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠1=x,
则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°-2x.
①AE=OD,理由如下:
在△AOE与△OCD中,
∴△AOE≌△OCD(SAS).
∴AE=OD.
②∵OE=OC,
∠6=∠1+∠2=2x,
∴∠5=∠6=2x,
∵AE∥OC,
∴∠4+∠5+∠6=180°,
即x+2x+2x=180°.
∴x=36°.
∴∠ODC=36°.
同课章节目录
