8.6.2 直线与平面垂直课件(共68张PPT)2020-2021年高一下学期数学人教版(2019)必修第二册第八章
文档属性
| 名称 | 8.6.2 直线与平面垂直课件(共68张PPT)2020-2021年高一下学期数学人教版(2019)必修第二册第八章 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 16:23:46 | ||
图片预览











文档简介
第八章 §8.6 空间直线、平面的垂直
8.6.2 直线与平面垂直
学习目标
XUE XI MU BIAO
1.了解直线与平面垂直的定义;了解直线与平面所成角的概念.
2.掌握直线与平面垂直的判定定理,并会用定理判定线面垂直.
3.掌握直线与平面垂直的性质定理,并会用定理证明相关问题.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 直线与平面垂直的定义
定义
如果直线l与平面α内的 直线都垂直,我们就说直线l与平面α互相垂直
记法
_____
有关概念
直线l叫做平面α的 ,平面α叫做直线l的 ,它们唯一的公共点P叫做_____
任意一条
l⊥α
垂线
垂面
垂足
图示
?
画法
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
注意:过一点垂直于已知平面的直线有且只有一条,该点与垂足间的线段叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
知识点二 直线与平面垂直的判定定理
文字语言
如果一条直线与一个平面内的 垂直,那么该直线与此平面垂直
符号语言
l⊥a,l⊥b,a?α,b?α, =P?l⊥α
图形语言
两条相交直线
a∩b
思考 若把定理中的“两条相交直线”改为“两条平行直线”,直线与平面一定垂直吗?
答案 当这两条直线平行时,直线可与平面平行或相交或在平面内,但不一定垂直.
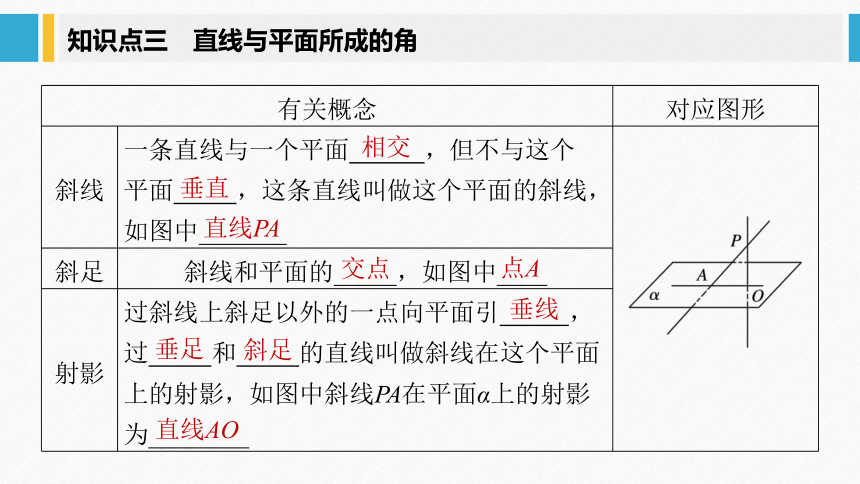
知识点三 直线与平面所成的角
有关概念
对应图形
斜线
一条直线与一个平面 ,但不与这个
平面 ,这条直线叫做这个平面的斜线,如图中_______
?
斜足
斜线和平面的_____,如图中____
射影
过斜线上斜足以外的一点向平面引 ,过 和 的直线叫做斜线在这个平面上的射影,如图中斜线PA在平面α上的射影为________
相交
垂直
直线PA
交点
点A
垂线
垂足
斜足
直线AO
直线与平面所成的角
定义:平面的一条斜线和它在平面上的
射影所成的角,如图中_______
规定:一条直线垂直于平面,它们所成
的角是 ;
一条直线和平面平行,或在平面内,它们所成的角是___
取值
范围
设直线与平面所成的角为θ,则____________
∠PAO
90°
0°
0°≤θ≤90°
知识点四 直线与平面垂直的性质定理
文字语言
垂直于同一个平面的两条直线______
符号语言
图形语言
?
a⊥α,
b⊥α
?a∥b
平行
注意:一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离,如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离.
思考 垂直于同一平面的两条垂线一定共面吗?
答案 共面,由线面垂直的性质定理可知这两条直线是平行的,故能确定一个平面.
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.若直线与平面所成角为α,则0°<α≤90°.( )
2.如果一条直线与一个平面垂直,则这条直线垂直于这个平面内的所有直线.( )
3.如果两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面.( )
√
×
√
2
题型探究
PART TWO
例1 (多选)下列命题中,不正确的是
A.若直线l与平面α内的一条直线垂直,则l⊥α
B.若直线l不垂直于平面α,则α内没有与l垂直的直线
C.若直线l不垂直于平面α,则α内也可以有无数条直线与l垂直
D.若直线l与平面α内的无数条直线垂直,则l⊥α
一、直线与平面垂直的定义以及判定定理的理解
√
√
√
解析 当l与α内的一条直线垂直时,不能保证l与平面α垂直,所以A不正确;
当l与α不垂直时,l可能与α内的无数条平行直线垂直,所以B不正确,C正确;
若l在α内,l也可以和α内的无数条直线垂直,故D错误.
反思感悟
对于线面垂直的定义要注意“直线垂直于平面内的所有直线”说法与“直线垂直于平面内无数条直线”不是一回事.
跟踪训练1 如果一条直线垂直于一个平面内的:①三角形的两边;②梯形的两边;③圆的两条直径;④正五边形的两边.能保证该直线与平面垂直的是________.(填序号)
①③④
解析 根据直线与平面垂直的判定定理,平面内这两条直线必须是相交的,①③④中给定的两直线一定相交,能保证直线与平面垂直,而②梯形的两边可能是上、下底边,它们互相平行,不满足定理条件.
二、直线与平面垂直的判定
例2 如图所示,在正方体ABCD-A1B1C1D1中,M为CC1的中点,AC与BD交于点O,求证:A1O⊥平面MBD.
证明 ∵四边形ABCD为正方形,
∴BD⊥AC,
又AA1⊥平面ABCD,
∴AA1⊥BD且AA1∩AC=A,
∴BD⊥平面AA1O,
∴BD⊥A1O,
令正方体的棱长为2,连接OM,A1M(图略),
∴A1O2+OM2=A1M2,
∴A1O⊥OM,
又OM∩BD=O,
∴A1O⊥平面MBD.
反思感悟
证明线面垂直的方法
(1)由线线垂直证明线面垂直:
①定义法(不常用);②判定定理(最常用),要着力寻找平面内的两条相交直线(有时需要作辅助线),使它们与所给直线垂直.
(2)平行转化法(利用推论):
①a∥b,a⊥α?b⊥α;②α∥β,a⊥α?a⊥β.
跟踪训练2 如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.
(1)求证:AN⊥平面PBM;
证明 ∵AB为⊙O的直径,∴AM⊥BM.
又PA⊥平面ABM,BM?平面ABM,∴PA⊥BM.
又∵PA∩AM=A,PA,AM?平面PAM,
又AN?平面PAM,∴BM⊥AN.
又AN⊥PM,且BM∩PM=M,BM,PM?平面PBM,
∴BM⊥平面PAM.
∴AN⊥平面PBM.
(2)若AQ⊥PB,垂足为Q,求证:NQ⊥PB.
证明 由(1)知AN⊥平面PBM,
PB?平面PBM,∴AN⊥PB.
又∵AQ⊥PB,AN∩AQ=A,AN,AQ?平面ANQ,
∴PB⊥平面ANQ.
又NQ?平面ANQ,∴PB⊥NQ.
三、直线与平面垂直的性质
例3 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB⊥平面PAD,AD=AP,E是PD的中点,M,N分别在AB,PC上,且MN⊥AB,MN⊥PC.证明:AE∥MN.
证明 ∵AB⊥平面PAD,AE?平面PAD,
∴AE⊥AB,
又AB∥CD,∴AE⊥CD.
∵AD=AP,E是PD的中点,∴AE⊥PD.
又CD∩PD=D,CD,PD?平面PCD,
∴AE⊥平面PCD.
∵MN⊥AB,AB∥CD,∴MN⊥CD.
又∵MN⊥PC,PC∩CD=C,PC,CD?平面PCD,
∴MN⊥平面PCD,∴AE∥MN.
反思感悟
证明线线平行的常用方法
(1)利用线线平行定义:证共面且无公共点.
(2)利用基本事实4:证两线同时平行于第三条直线.
(3)利用线面平行的性质定理:把证线线平行转化为证线面平行.
(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直.
(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.
跟踪训练3 如图,α∩β=l,PA⊥α,PB⊥β,垂足分别为A,B,a?α,a⊥AB.求证:a∥l.
证明 ∵PA⊥α,l?α,∴PA⊥l.
同理PB⊥l.
∵PA∩PB=P,PA,PB?平面PAB,∴l⊥平面PAB.
又∵PA⊥α,a?α,∴PA⊥a.
∵a⊥AB,PA∩AB=A,PA,AB?平面PAB,
∴a⊥平面PAB.
∴a∥l.
核心素养之直观想象和逻辑推理
HE XIN SU YANG ZHI ZHI GUAN XIANG XIANG HE LUO JI TUI LI
求直线与平面所成的角
典例 如图,在正方体ABCD-A1B1C1D1中.
(1)求A1B与平面AA1D1D所成的角;
解 ∵AB⊥平面AA1D1D,
∴∠AA1B就是A1B与平面AA1D1D所成的角,
在Rt△AA1B中,∠BAA1=90°,AB=AA1,
∴∠AA1B=45°,
∴A1B与平面AA1D1D所成的角是45°.
(2)求A1B与平面BB1D1D所成的角.
解 连接A1C1交B1D1于点O,连接BO.
∵A1O⊥B1D1,BB1⊥A1O,BB1∩B1D1=B1,BB1,B1D1?平面BB1D1D,
∴A1O⊥平面BB1D1D,
∴∠A1BO就是A1B与平面BB1D1D所成的角.
又∵∠A1OB=90°,
∴∠A1BO=30°,
∴A1B与平面BB1D1D所成的角是30°.
素养提升
(1)求直线与平面所成角的关键是寻找过直线上一点与平面垂直的垂线、垂足与斜足的连线即为直线在平面内的射影,直线与直线在平面内射影所成的角即为线面角.
(2)通过作辅助线找垂线,确定线面角,提升直观想象、逻辑推理的素养.
3
随堂演练
PART THREE
1.给出下列三个命题:
①一条直线垂直于一个平面内的三条直线,则这条直线和这个平面垂直;
②一条直线与一个平面内的任何直线所成的角相等,则这条直线和这个平面垂直;
③一条直线垂直于平面内的任意一条直线,则这条直线与这个平面垂直.
其中正确的个数是
A.0 B.1 C.2 D.3
1
2
3
4
5
√
解析 ①错,②③对.
1
2
3
4
5
2.(多选)下列命题正确的是
√
√
√
3.若点A,B在平面α的同侧,则点A,B到α的距离分别为3和5,则AB的中点到α的距离为
A.4 B.3 C.2 D.1
√
解析 如图,∵AC⊥α,BD⊥α,
∴AC∥BD,又AC=3,BD=5,EF为中位线,EF∥AC,
1
2
3
4
5
4.如图,在正方体ABCD-A1B1C1D1中,与AD1垂直的平面是
A.平面DD1C1C B.平面A1DB1
C.平面A1B1C1D1 D.平面A1DB
1
2
3
4
5
√
解析 ∵AD1⊥A1D,AD1⊥A1B1,A1D∩A1B1=A1,A1D,A1B1?平面A1DB1,
∴AD1⊥平面A1DB1.
1
2
3
4
5
5.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成角的度数为________.
45°
解析 因为PA⊥平面ABC,所以斜线PB在平面ABC上的射影为AB,
所以∠PBA即为直线PB与平面ABC所成的角.
在△PAB中,∠BAP=90°,PA=AB,所以∠PBA=45°,
即直线PB与平面ABC所成的角等于45°.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)直线与平面垂直的定义.
(2)直线与平面垂直的判定定理.
(3)直线与平面垂直的性质定理.
2.方法归纳:转化思想.
3.常见误区:判定定理理解“平面内找两条相交直线”与该直线垂直.
4
课时对点练
PART FOUR
基础巩固
1.已知△ABC,若直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则l,m的位置关系是
A.相交 B.异面
C.平行 D.不确定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 依题意知l⊥平面ABC,m⊥平面ABC,
∴l∥m.
2.下列说法中,正确的有
①如果一条直线垂直于平面内的四条直线,那么这条直线和这个平面垂直;
②过直线l外一点P,有且仅有一个平面与l垂直;
③如果三条共点直线两两垂直,那么其中一条直线垂直于另两条直线确定的平面;
④过点A垂直于直线a的所有直线都在过点A垂直于a的平面内.
A.1个 B.2个 C.3个 D.4个
√
解析 ①不正确,其他三项均正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.如图,α∩β=l,点A,C∈α,点B∈β,且BA⊥α,BC⊥β,那么直线l与直线AC的关系是
A.异面 B.平行
C.垂直 D.不确定
√
解析 ∵AB⊥α,l?α,∴AB⊥l,
又∵BC⊥β,l?β,∴BC⊥l,
又AB∩BC=B,AB,BC?平面ABC,
∴l⊥平面ABC,
又AC?平面ABC,∴l⊥AC.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.如图,三棱柱ABC-A1B1C1的各棱长均相等,且侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面ABC所成的角为
A.30° B.45°
C.60° D.90°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
5.如图所示,定点A和B都在平面α内,定点P?α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 易证AC⊥平面PBC,又BC?平面PBC,
所以AC⊥BC.
6.平行四边形ABCD的对角线交点为O,点P在平行四边形ABCD所在平面外,且PA=PC,PD=PB,则PO与平面ABCD的位置关系是________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
垂直
解析 在△PAC中,PA=PC,O为AC的中点,
∴PO⊥AC,
同理PO⊥BD,又AC∩BD=O,
∴PO⊥平面ABCD.
7.在长方体ABCD-A1B1C1D1中,E∈BD,F∈B1D1,且EF⊥AB,则EF与AA1的位置关系是______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
平行
解析 如图,∵AB⊥BB1,AB⊥EF,且AB不垂直于平面BB1D1D,
∴EF与BB1不相交,∴EF∥BB1,
又AA1∥BB1,∴EF∥AA1.
8.在矩形ABCD中,AB=1,BC= ,PA⊥平面ABCD,PA=1,则PC与平面ABCD所成的角是______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
30°
解析 由题意知∠PCA为PC与平面ABCD所成的角.
∴∠PCA=30°.
9.如图所示,四边形ABCD是正方形,DE⊥平面ABCD,DE=DA=2.
(1)求证:AC⊥平面BDE;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 ∵四边形ABCD是正方形,∴AC⊥BD.
∵DE⊥平面ABCD,AC?平面ABCD,∴AC⊥DE,
∵BD,DE?平面BED,BD∩DE=D,
∴AC⊥平面BDE.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求AE与平面BDE所成角的大小.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设AC∩BD=O,连接EO,如图所示.
∵AC⊥平面BDE,∴EO是直线AE在平面BDE上的射影,
∴∠AEO即为AE与平面BDE所成的角.
∴∠AEO=30°,即AE与平面BDE所成的角为30°.
10.如图,在正方体ABCD-A1B1C1D1中,EF与异面直线AC,A1D都垂直.求证:EF∥BD1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 如图所示,连接AB1,B1D1,B1C,BD,
∵DD1⊥平面ABCD,AC?平面ABCD,∴DD1⊥AC.
又AC⊥BD,DD1∩BD=D,DD1,BD?平面BDD1B1,
∴AC⊥平面BDD1B1,
又BD1?平面BDD1B1,
∴AC⊥BD1.
同理可证BD1⊥B1C,
又AC∩B1C=C,AC,B1C?平面AB1C,
∴BD1⊥平面AB1C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵EF⊥A1D,A1D∥B1C,∴EF⊥B1C.
又∵EF⊥AC,AC∩B1C=C,AC,B1C?平面AB1C,
∴EF⊥平面AB1C,∴EF∥BD1.
综合运用
11.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,那么,在这个空间图形中必有
A.AG⊥△EFH所在平面
B.AH⊥△EFH所在平面
C.HF⊥△AEF所在平面
D.HG⊥△AEF所在平面
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 根据折叠前、后AH⊥HE,AH⊥HF不变,可推出AH⊥平面EFH.
12.在四面体P-ABC中,若PA=PB=PC,则点P在平面ABC内的射影一定是△ABC的
A.外心 B.内心 C.垂心 D.重心
√
解析 如图,设点P在平面ABC内的射影为点O,连接OP,则PO⊥平面ABC,
连接OA,OB,OC,
∴PO⊥OA,PO⊥OB,PO⊥OC,
又PA=PB=PC,
∴Rt△POA≌Rt△POB≌Rt△POC,
则OA=OB=OC,
∴O为△ABC的外心.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.如图所示,在正三棱柱ABC-A1B1C1中,若AB∶BB1= ∶1,则AB1与平面BB1C1C所成角的大小为
A.45° B.60°
C.30° D.75°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 取BC的中点D,连接AD,B1D,
∵AD⊥BC且AD⊥BB1,BC∩BB1=B,BC,BB1?平面BCC1B1,
∴AD⊥平面BCC1B1,
∴∠AB1D即为AB1与平面BB1C1C所成的角.
即AB1与平面BB1C1C所成的角为45°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.如图,在直三棱柱ABC-A1B1C1中,BC=CC1,当底面A1B1C1满足条件_______________时,有AB1⊥BC1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∠A1C1B1=90°
解析 如图所示,连接B1C,
由BC=CC1,可得BC1⊥B1C,
因此,要证AB1⊥BC1,
则只要证明BC1⊥平面AB1C,
即只要证AC⊥BC1即可,
由直三棱柱可知,只要证AC⊥BC即可.
因为A1C1∥AC,B1C1∥BC,
故只要证A1C1⊥B1C1即可.(或者能推出A1C1⊥B1C1的条件,如∠A1C1B1=90°等)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.(多选)如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中正确的是
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD
所成的角
D.AB与SC所成的角等于DC与SA所成的角
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 对于选项A,由题意得SD⊥AC,AC⊥BD,SD∩BD=D,SD,BD?平面SBD,∴AC⊥平面SBD,故AC⊥SB,故A正确;
对于选项B,∵AB∥CD,AB?平面SCD,CD?平面SCD,∴AB∥平面SCD,故B正确;
对于选项C,由对称性知SA与平面SBD所成的角与SC与平面SBD所成的角相等,故C正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图,PA⊥矩形ABCD所在的平面,M,N分别是AB,PC的中点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求证:MN∥平面PAD;
证明 取PD的中点E,连接NE,AE,如图.
又∵N是PC的中点,
又∵DC∥AB且DC=AB,
∴四边形AMNE是平行四边形,∴MN∥AE.
∵AE?平面PAD,MN?平面PAD,
∴MN∥平面PAD.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若PD与平面ABCD所成的角为α,当α为多少度时,MN⊥平面PCD?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当α=45°时,MN⊥平面PCD,证明如下.
∵PA⊥平面ABCD,
∴∠PDA即为PD与平面ABCD所成的角,
∴∠PDA=45°,∴AP=AD,∴AE⊥PD.
又∵MN∥AE,∴MN⊥PD.
∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD.
又∵CD⊥AD,PA∩AD=A,PA,AD?平面PAD,
∴CD⊥平面PAD.
∵AE?平面PAD,
∴CD⊥AE,
∴CD⊥MN.
又CD∩PD=D,CD,PD?平面PCD,
∴MN⊥平面PCD.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
8.6.2 直线与平面垂直
学习目标
XUE XI MU BIAO
1.了解直线与平面垂直的定义;了解直线与平面所成角的概念.
2.掌握直线与平面垂直的判定定理,并会用定理判定线面垂直.
3.掌握直线与平面垂直的性质定理,并会用定理证明相关问题.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 直线与平面垂直的定义
定义
如果直线l与平面α内的 直线都垂直,我们就说直线l与平面α互相垂直
记法
_____
有关概念
直线l叫做平面α的 ,平面α叫做直线l的 ,它们唯一的公共点P叫做_____
任意一条
l⊥α
垂线
垂面
垂足
图示
?
画法
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
注意:过一点垂直于已知平面的直线有且只有一条,该点与垂足间的线段叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
知识点二 直线与平面垂直的判定定理
文字语言
如果一条直线与一个平面内的 垂直,那么该直线与此平面垂直
符号语言
l⊥a,l⊥b,a?α,b?α, =P?l⊥α
图形语言
两条相交直线
a∩b
思考 若把定理中的“两条相交直线”改为“两条平行直线”,直线与平面一定垂直吗?
答案 当这两条直线平行时,直线可与平面平行或相交或在平面内,但不一定垂直.
知识点三 直线与平面所成的角
有关概念
对应图形
斜线
一条直线与一个平面 ,但不与这个
平面 ,这条直线叫做这个平面的斜线,如图中_______
?
斜足
斜线和平面的_____,如图中____
射影
过斜线上斜足以外的一点向平面引 ,过 和 的直线叫做斜线在这个平面上的射影,如图中斜线PA在平面α上的射影为________
相交
垂直
直线PA
交点
点A
垂线
垂足
斜足
直线AO
直线与平面所成的角
定义:平面的一条斜线和它在平面上的
射影所成的角,如图中_______
规定:一条直线垂直于平面,它们所成
的角是 ;
一条直线和平面平行,或在平面内,它们所成的角是___
取值
范围
设直线与平面所成的角为θ,则____________
∠PAO
90°
0°
0°≤θ≤90°
知识点四 直线与平面垂直的性质定理
文字语言
垂直于同一个平面的两条直线______
符号语言
图形语言
?
a⊥α,
b⊥α
?a∥b
平行
注意:一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离,如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离.
思考 垂直于同一平面的两条垂线一定共面吗?
答案 共面,由线面垂直的性质定理可知这两条直线是平行的,故能确定一个平面.
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.若直线与平面所成角为α,则0°<α≤90°.( )
2.如果一条直线与一个平面垂直,则这条直线垂直于这个平面内的所有直线.( )
3.如果两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面.( )
√
×
√
2
题型探究
PART TWO
例1 (多选)下列命题中,不正确的是
A.若直线l与平面α内的一条直线垂直,则l⊥α
B.若直线l不垂直于平面α,则α内没有与l垂直的直线
C.若直线l不垂直于平面α,则α内也可以有无数条直线与l垂直
D.若直线l与平面α内的无数条直线垂直,则l⊥α
一、直线与平面垂直的定义以及判定定理的理解
√
√
√
解析 当l与α内的一条直线垂直时,不能保证l与平面α垂直,所以A不正确;
当l与α不垂直时,l可能与α内的无数条平行直线垂直,所以B不正确,C正确;
若l在α内,l也可以和α内的无数条直线垂直,故D错误.
反思感悟
对于线面垂直的定义要注意“直线垂直于平面内的所有直线”说法与“直线垂直于平面内无数条直线”不是一回事.
跟踪训练1 如果一条直线垂直于一个平面内的:①三角形的两边;②梯形的两边;③圆的两条直径;④正五边形的两边.能保证该直线与平面垂直的是________.(填序号)
①③④
解析 根据直线与平面垂直的判定定理,平面内这两条直线必须是相交的,①③④中给定的两直线一定相交,能保证直线与平面垂直,而②梯形的两边可能是上、下底边,它们互相平行,不满足定理条件.
二、直线与平面垂直的判定
例2 如图所示,在正方体ABCD-A1B1C1D1中,M为CC1的中点,AC与BD交于点O,求证:A1O⊥平面MBD.
证明 ∵四边形ABCD为正方形,
∴BD⊥AC,
又AA1⊥平面ABCD,
∴AA1⊥BD且AA1∩AC=A,
∴BD⊥平面AA1O,
∴BD⊥A1O,
令正方体的棱长为2,连接OM,A1M(图略),
∴A1O2+OM2=A1M2,
∴A1O⊥OM,
又OM∩BD=O,
∴A1O⊥平面MBD.
反思感悟
证明线面垂直的方法
(1)由线线垂直证明线面垂直:
①定义法(不常用);②判定定理(最常用),要着力寻找平面内的两条相交直线(有时需要作辅助线),使它们与所给直线垂直.
(2)平行转化法(利用推论):
①a∥b,a⊥α?b⊥α;②α∥β,a⊥α?a⊥β.
跟踪训练2 如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.
(1)求证:AN⊥平面PBM;
证明 ∵AB为⊙O的直径,∴AM⊥BM.
又PA⊥平面ABM,BM?平面ABM,∴PA⊥BM.
又∵PA∩AM=A,PA,AM?平面PAM,
又AN?平面PAM,∴BM⊥AN.
又AN⊥PM,且BM∩PM=M,BM,PM?平面PBM,
∴BM⊥平面PAM.
∴AN⊥平面PBM.
(2)若AQ⊥PB,垂足为Q,求证:NQ⊥PB.
证明 由(1)知AN⊥平面PBM,
PB?平面PBM,∴AN⊥PB.
又∵AQ⊥PB,AN∩AQ=A,AN,AQ?平面ANQ,
∴PB⊥平面ANQ.
又NQ?平面ANQ,∴PB⊥NQ.
三、直线与平面垂直的性质
例3 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB⊥平面PAD,AD=AP,E是PD的中点,M,N分别在AB,PC上,且MN⊥AB,MN⊥PC.证明:AE∥MN.
证明 ∵AB⊥平面PAD,AE?平面PAD,
∴AE⊥AB,
又AB∥CD,∴AE⊥CD.
∵AD=AP,E是PD的中点,∴AE⊥PD.
又CD∩PD=D,CD,PD?平面PCD,
∴AE⊥平面PCD.
∵MN⊥AB,AB∥CD,∴MN⊥CD.
又∵MN⊥PC,PC∩CD=C,PC,CD?平面PCD,
∴MN⊥平面PCD,∴AE∥MN.
反思感悟
证明线线平行的常用方法
(1)利用线线平行定义:证共面且无公共点.
(2)利用基本事实4:证两线同时平行于第三条直线.
(3)利用线面平行的性质定理:把证线线平行转化为证线面平行.
(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直.
(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.
跟踪训练3 如图,α∩β=l,PA⊥α,PB⊥β,垂足分别为A,B,a?α,a⊥AB.求证:a∥l.
证明 ∵PA⊥α,l?α,∴PA⊥l.
同理PB⊥l.
∵PA∩PB=P,PA,PB?平面PAB,∴l⊥平面PAB.
又∵PA⊥α,a?α,∴PA⊥a.
∵a⊥AB,PA∩AB=A,PA,AB?平面PAB,
∴a⊥平面PAB.
∴a∥l.
核心素养之直观想象和逻辑推理
HE XIN SU YANG ZHI ZHI GUAN XIANG XIANG HE LUO JI TUI LI
求直线与平面所成的角
典例 如图,在正方体ABCD-A1B1C1D1中.
(1)求A1B与平面AA1D1D所成的角;
解 ∵AB⊥平面AA1D1D,
∴∠AA1B就是A1B与平面AA1D1D所成的角,
在Rt△AA1B中,∠BAA1=90°,AB=AA1,
∴∠AA1B=45°,
∴A1B与平面AA1D1D所成的角是45°.
(2)求A1B与平面BB1D1D所成的角.
解 连接A1C1交B1D1于点O,连接BO.
∵A1O⊥B1D1,BB1⊥A1O,BB1∩B1D1=B1,BB1,B1D1?平面BB1D1D,
∴A1O⊥平面BB1D1D,
∴∠A1BO就是A1B与平面BB1D1D所成的角.
又∵∠A1OB=90°,
∴∠A1BO=30°,
∴A1B与平面BB1D1D所成的角是30°.
素养提升
(1)求直线与平面所成角的关键是寻找过直线上一点与平面垂直的垂线、垂足与斜足的连线即为直线在平面内的射影,直线与直线在平面内射影所成的角即为线面角.
(2)通过作辅助线找垂线,确定线面角,提升直观想象、逻辑推理的素养.
3
随堂演练
PART THREE
1.给出下列三个命题:
①一条直线垂直于一个平面内的三条直线,则这条直线和这个平面垂直;
②一条直线与一个平面内的任何直线所成的角相等,则这条直线和这个平面垂直;
③一条直线垂直于平面内的任意一条直线,则这条直线与这个平面垂直.
其中正确的个数是
A.0 B.1 C.2 D.3
1
2
3
4
5
√
解析 ①错,②③对.
1
2
3
4
5
2.(多选)下列命题正确的是
√
√
√
3.若点A,B在平面α的同侧,则点A,B到α的距离分别为3和5,则AB的中点到α的距离为
A.4 B.3 C.2 D.1
√
解析 如图,∵AC⊥α,BD⊥α,
∴AC∥BD,又AC=3,BD=5,EF为中位线,EF∥AC,
1
2
3
4
5
4.如图,在正方体ABCD-A1B1C1D1中,与AD1垂直的平面是
A.平面DD1C1C B.平面A1DB1
C.平面A1B1C1D1 D.平面A1DB
1
2
3
4
5
√
解析 ∵AD1⊥A1D,AD1⊥A1B1,A1D∩A1B1=A1,A1D,A1B1?平面A1DB1,
∴AD1⊥平面A1DB1.
1
2
3
4
5
5.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成角的度数为________.
45°
解析 因为PA⊥平面ABC,所以斜线PB在平面ABC上的射影为AB,
所以∠PBA即为直线PB与平面ABC所成的角.
在△PAB中,∠BAP=90°,PA=AB,所以∠PBA=45°,
即直线PB与平面ABC所成的角等于45°.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)直线与平面垂直的定义.
(2)直线与平面垂直的判定定理.
(3)直线与平面垂直的性质定理.
2.方法归纳:转化思想.
3.常见误区:判定定理理解“平面内找两条相交直线”与该直线垂直.
4
课时对点练
PART FOUR
基础巩固
1.已知△ABC,若直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则l,m的位置关系是
A.相交 B.异面
C.平行 D.不确定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 依题意知l⊥平面ABC,m⊥平面ABC,
∴l∥m.
2.下列说法中,正确的有
①如果一条直线垂直于平面内的四条直线,那么这条直线和这个平面垂直;
②过直线l外一点P,有且仅有一个平面与l垂直;
③如果三条共点直线两两垂直,那么其中一条直线垂直于另两条直线确定的平面;
④过点A垂直于直线a的所有直线都在过点A垂直于a的平面内.
A.1个 B.2个 C.3个 D.4个
√
解析 ①不正确,其他三项均正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.如图,α∩β=l,点A,C∈α,点B∈β,且BA⊥α,BC⊥β,那么直线l与直线AC的关系是
A.异面 B.平行
C.垂直 D.不确定
√
解析 ∵AB⊥α,l?α,∴AB⊥l,
又∵BC⊥β,l?β,∴BC⊥l,
又AB∩BC=B,AB,BC?平面ABC,
∴l⊥平面ABC,
又AC?平面ABC,∴l⊥AC.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.如图,三棱柱ABC-A1B1C1的各棱长均相等,且侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面ABC所成的角为
A.30° B.45°
C.60° D.90°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
5.如图所示,定点A和B都在平面α内,定点P?α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 易证AC⊥平面PBC,又BC?平面PBC,
所以AC⊥BC.
6.平行四边形ABCD的对角线交点为O,点P在平行四边形ABCD所在平面外,且PA=PC,PD=PB,则PO与平面ABCD的位置关系是________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
垂直
解析 在△PAC中,PA=PC,O为AC的中点,
∴PO⊥AC,
同理PO⊥BD,又AC∩BD=O,
∴PO⊥平面ABCD.
7.在长方体ABCD-A1B1C1D1中,E∈BD,F∈B1D1,且EF⊥AB,则EF与AA1的位置关系是______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
平行
解析 如图,∵AB⊥BB1,AB⊥EF,且AB不垂直于平面BB1D1D,
∴EF与BB1不相交,∴EF∥BB1,
又AA1∥BB1,∴EF∥AA1.
8.在矩形ABCD中,AB=1,BC= ,PA⊥平面ABCD,PA=1,则PC与平面ABCD所成的角是______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
30°
解析 由题意知∠PCA为PC与平面ABCD所成的角.
∴∠PCA=30°.
9.如图所示,四边形ABCD是正方形,DE⊥平面ABCD,DE=DA=2.
(1)求证:AC⊥平面BDE;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 ∵四边形ABCD是正方形,∴AC⊥BD.
∵DE⊥平面ABCD,AC?平面ABCD,∴AC⊥DE,
∵BD,DE?平面BED,BD∩DE=D,
∴AC⊥平面BDE.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求AE与平面BDE所成角的大小.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设AC∩BD=O,连接EO,如图所示.
∵AC⊥平面BDE,∴EO是直线AE在平面BDE上的射影,
∴∠AEO即为AE与平面BDE所成的角.
∴∠AEO=30°,即AE与平面BDE所成的角为30°.
10.如图,在正方体ABCD-A1B1C1D1中,EF与异面直线AC,A1D都垂直.求证:EF∥BD1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明 如图所示,连接AB1,B1D1,B1C,BD,
∵DD1⊥平面ABCD,AC?平面ABCD,∴DD1⊥AC.
又AC⊥BD,DD1∩BD=D,DD1,BD?平面BDD1B1,
∴AC⊥平面BDD1B1,
又BD1?平面BDD1B1,
∴AC⊥BD1.
同理可证BD1⊥B1C,
又AC∩B1C=C,AC,B1C?平面AB1C,
∴BD1⊥平面AB1C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵EF⊥A1D,A1D∥B1C,∴EF⊥B1C.
又∵EF⊥AC,AC∩B1C=C,AC,B1C?平面AB1C,
∴EF⊥平面AB1C,∴EF∥BD1.
综合运用
11.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,那么,在这个空间图形中必有
A.AG⊥△EFH所在平面
B.AH⊥△EFH所在平面
C.HF⊥△AEF所在平面
D.HG⊥△AEF所在平面
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 根据折叠前、后AH⊥HE,AH⊥HF不变,可推出AH⊥平面EFH.
12.在四面体P-ABC中,若PA=PB=PC,则点P在平面ABC内的射影一定是△ABC的
A.外心 B.内心 C.垂心 D.重心
√
解析 如图,设点P在平面ABC内的射影为点O,连接OP,则PO⊥平面ABC,
连接OA,OB,OC,
∴PO⊥OA,PO⊥OB,PO⊥OC,
又PA=PB=PC,
∴Rt△POA≌Rt△POB≌Rt△POC,
则OA=OB=OC,
∴O为△ABC的外心.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.如图所示,在正三棱柱ABC-A1B1C1中,若AB∶BB1= ∶1,则AB1与平面BB1C1C所成角的大小为
A.45° B.60°
C.30° D.75°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 取BC的中点D,连接AD,B1D,
∵AD⊥BC且AD⊥BB1,BC∩BB1=B,BC,BB1?平面BCC1B1,
∴AD⊥平面BCC1B1,
∴∠AB1D即为AB1与平面BB1C1C所成的角.
即AB1与平面BB1C1C所成的角为45°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.如图,在直三棱柱ABC-A1B1C1中,BC=CC1,当底面A1B1C1满足条件_______________时,有AB1⊥BC1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∠A1C1B1=90°
解析 如图所示,连接B1C,
由BC=CC1,可得BC1⊥B1C,
因此,要证AB1⊥BC1,
则只要证明BC1⊥平面AB1C,
即只要证AC⊥BC1即可,
由直三棱柱可知,只要证AC⊥BC即可.
因为A1C1∥AC,B1C1∥BC,
故只要证A1C1⊥B1C1即可.(或者能推出A1C1⊥B1C1的条件,如∠A1C1B1=90°等)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.(多选)如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中正确的是
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD
所成的角
D.AB与SC所成的角等于DC与SA所成的角
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 对于选项A,由题意得SD⊥AC,AC⊥BD,SD∩BD=D,SD,BD?平面SBD,∴AC⊥平面SBD,故AC⊥SB,故A正确;
对于选项B,∵AB∥CD,AB?平面SCD,CD?平面SCD,∴AB∥平面SCD,故B正确;
对于选项C,由对称性知SA与平面SBD所成的角与SC与平面SBD所成的角相等,故C正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图,PA⊥矩形ABCD所在的平面,M,N分别是AB,PC的中点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求证:MN∥平面PAD;
证明 取PD的中点E,连接NE,AE,如图.
又∵N是PC的中点,
又∵DC∥AB且DC=AB,
∴四边形AMNE是平行四边形,∴MN∥AE.
∵AE?平面PAD,MN?平面PAD,
∴MN∥平面PAD.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若PD与平面ABCD所成的角为α,当α为多少度时,MN⊥平面PCD?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当α=45°时,MN⊥平面PCD,证明如下.
∵PA⊥平面ABCD,
∴∠PDA即为PD与平面ABCD所成的角,
∴∠PDA=45°,∴AP=AD,∴AE⊥PD.
又∵MN∥AE,∴MN⊥PD.
∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD.
又∵CD⊥AD,PA∩AD=A,PA,AD?平面PAD,
∴CD⊥平面PAD.
∵AE?平面PAD,
∴CD⊥AE,
∴CD⊥MN.
又CD∩PD=D,CD,PD?平面PCD,
∴MN⊥平面PCD.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
