6.4.1 平面几何中的向量方法~6.4.2 向量在物理中的应用举例 课件(共55张PPT)2020-2021年高一下学期数学人教版(2019)必修第二册第六章
文档属性
| 名称 | 6.4.1 平面几何中的向量方法~6.4.2 向量在物理中的应用举例 课件(共55张PPT)2020-2021年高一下学期数学人教版(2019)必修第二册第六章 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览








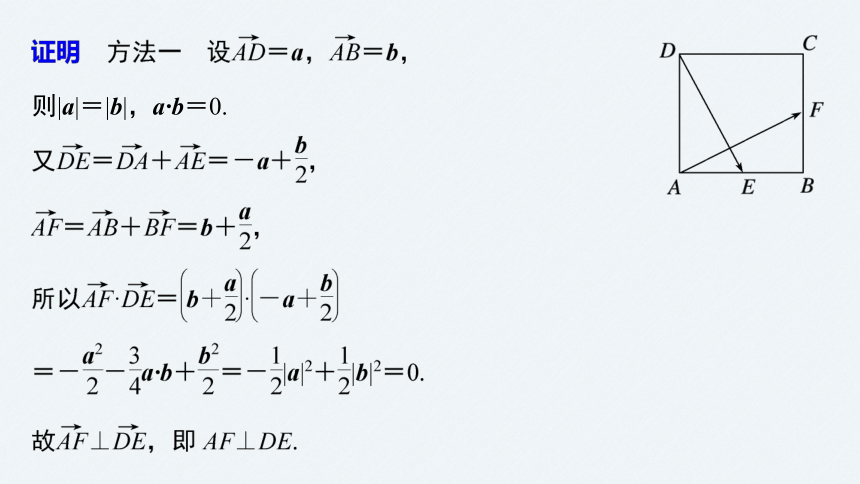


文档简介
第六章 §6.4 平面向量的应用
6.4.1 平面几何中的向量方法
6.4.2 向量在物理中的应用举例
学习目标
XUE XI MU BIAO
1.能用向量方法解决简单的几何问题.
2.能用向量方法解决简单的力学问题和其他实际问题.
3.体会向量在解决数学和实际问题中的作用,培养学生的运算、
分析和解决实际问题的能力.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
用向量方法解决平面几何问题的“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为 问题.
(2)通过 ,研究几何元素之间的关系,如距离、夹角等问题.
(3)把运算结果“ ”成几何关系.
知识点一 向量方法解决平面几何问题的步骤
向量
向量运算
翻译
(1)物理问题中常见的向量有 等.
(2)向量的加减法运算体现在 .
(3)动量mv是向量的 运算.
(4)功是 与 的数量积.
知识点二 向量在物理中的应用
力、速度、加速度、位移
力、速度、加速度、位移的合成与分解
数乘
力F
所产生的位移s
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.若△ABC为直角三角形,则有 =0.( )
2.若向量 ,则AB∥CD.( )
3.功是力F与位移s的数量积.( )
4.力的合成与分解体现了向量的加减法运算.( )
√
×
√
×
2
题型探究
PART TWO
一、利用向量证明平面几何问题
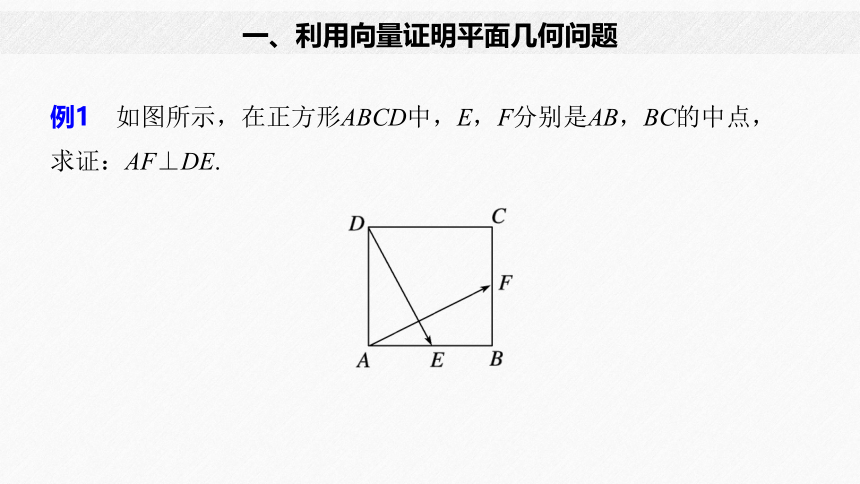
例1 如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
则|a|=|b|,a·b=0.
方法二 如图所示,建立平面直角坐标系,设正方形的边长为2,则A(0,0),D(0,2),E(1,0),F(2,1),
=2-2=0,
反思感悟
用向量证明平面几何问题的两种基本思路
(1)向量的线性运算法的四个步骤:
①选取基底;
②用基底表示相关向量;
③利用向量的线性运算或数量积找到相应关系;
④把计算所得结果转化为几何问题.
(2)向量的坐标运算法的四个步骤:
①建立适当的平面直角坐标系;
②把相关向量坐标化;
③利用向量的坐标运算找到相应关系;
④利用向量关系回答几何问题.
跟踪训练1 如图所示,在平行四边形ABCD中,BC=2BA,∠ABC=60°,作AE⊥BD交BC于点E,求BE∶EC.
即(λb-a)·(a+b)=0,
方法二 以B为坐标原点,BC所在直线为x轴建立平面直角坐标系,设B(0,0),C(2,0),
二、利用平面向量求几何中的长度问题
例2 在平行四边形ABCD中,AD=1,AB=2,对角线BD=2,求对角线AC的长.
反思感悟
用向量法求长度的策略
(1)根据图形特点选择基底,利用向量的数量积转化,用公式|a|2=a2求解.
(2)建立坐标系,确定相应向量的坐标,代入公式:若a=(x,y),则|a|= .
跟踪训练2 在△ABC中,已知A(4,1),B(7,5),C(-4,7),则BC边上的中线AD的长是
√
三、向量在物理中的应用
例3 一条宽为 km的河,水流速度为2 km/h,在河两岸有两个码头A,B,已知AB= km,船在水中的最大航速为4 km/h,问该船怎样安排航行速度可使它从A码头最快到达彼岸B码头?用时多少?
以AC和AD为邻边作?ACED,且当AE与AB重合时能最快到达彼岸,
根据题意知AC⊥AE,在Rt△ADE和?ACED中,
∴∠EAD=30°.
答 该船实际航行速度大小为4 km/h,与水流方向成120°角时能最快到达B码头,用时0.5 h.
反思感悟
用向量解决物理问题的一般步骤
(1)问题的转化,即把物理问题转化为数学问题.
(2)模型的建立,即建立以向量为主体的数学模型.
(3)参数的获得,即求出数学模型的有关解——理论参数值.
(4)问题的答案,即回到问题的初始状态,解释相关的物理现象.
跟踪训练3 一物体在力F1=(3,-4),F2=(2,-5),F3=(3,1)的共同作用下从点A(1,1)移动到点B(0,5).在这个过程中三个力的合力所做的功为________.
-40
解析 ∵F1=(3,-4),F2=(2,-5),F3=(3,1),
∴合力F=F1+F2+F3=(8,-8).
即三个力的合力做的功等于-40.
核心素养之逻辑推理、数学建模
HE XIN SU YANG ZHI LUO JI TUI LI SHU XUE JIAN MO
平面几何中的平行(或共线)问题
典例 如图,点O是平行四边形ABCD的中心,E,F分别在边CD,
AB上,且
求证:点E,O,F在同一直线上.
知E,F分别是CD,AB的三等分点,
故点E,O,F在同一直线上.
素养提升
(1)利用向量方法可以解决平面几何中的平行(共线)等问题,有两种思路:一种思路是选择一组基底,利用基向量表示涉及的向量,另一种思路是建立坐标系,求出题目中涉及的向量的坐标.
(2)通过用向量方法解决平面几何问题,培养数学建模、逻辑推理素养.
3
随堂演练
PART THREE
1.人骑自行车的速度是v1,风速为v2,则逆风行驶的速度为
A.v1-v2 B.v1+v2
C.|v1|-|v2| D.
√
1
2
3
4
5
解析 由向量的加法法则可得逆风行驶的速度为v1+v2.
注意速度是有方向和大小的,是一个向量.故选B.
A.是正三角形 B.是直角三角形
C.是等腰三角形 D.形状无法确定
√
∴CA=CB,则△ABC是等腰三角形.
1
2
3
4
5
3.已知A,B,C,D四点的坐标分别为(1,0),(4,3),(2,4),(0,2),则此四边形为
A.梯形 B.菱形
C.矩形 D.正方形
√
1
2
3
4
5
4.当两人提起重量为|G|的旅行包时,两人用力方向的夹角为θ,用力大小都为|F|,若|F|=|G|,则θ的值为
A.30° B.60° C.90° D.120°
√
当|F1|=|F2|=|G|时,△OAC为正三角形,
所以∠AOC=60°,从而∠AOB=120°.
1
2
3
4
5
1
2
3
4
5
=______.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)平面几何中的向量方法.
(2)向量在物理中的应用.
2.方法归纳:化归转化、数形结合.
3.常见误区:要注意选择恰当的基底.
4
课时对点练
PART FOUR
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.已知力F的大小|F|=10,在F的作用下产生的位移s的大小|s|=14,F与s的夹角为60°,则F做的功为
A.7 B.10
C.14 D.70
√
2.已知点A(-2,-3),B(19,4),C(-1,-6),则△ABC是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
∴△ABC为直角三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(多选)关于船从两平行河岸的一岸驶向另一岸所用的时间,正确的是
A.船垂直到达对岸所用时间最少
B.当船速v的方向与河岸垂直时用时最少
C.沿任意直线运动到达对岸的时间都一样
D.船垂直到达对岸时航行的距离最短
√
√
解析 根据向量将船速v分解,当v垂直河岸时,用时最少.
船垂直到达对岸时航行的距离最短.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.三个内角的角平分线的交点
B.三条边的垂直平分线的交点
C.三条中线的交点
D.三条高所在直线的交点
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
同理OA⊥BC,OC⊥AB,
∴O为三条高所在直线的交点.
√
∴四边形ABCD的面积
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
∴AP为Rt△ABC斜边BC的中线.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.一条河宽为8 000 m,一船从A处出发垂直航行到达河正对岸的B处,船速为20 km/h,水速为12 km/h,则船到达B处所需时间为_____ h.
0.5
解析 如图,v实际=v船+v水=v1+v2,
|v1|=20,|v2|=12,
∴该船到达B处所需的时间为0.5 h.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,以A为坐标原点,以AB所在直线为x轴,以AD所在直线为y轴建立平面直角坐标系,
则A(0,0),B(2,0),D(0,1),∴C(2,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.如图所示,若D是△ABC内的一点,且AB2-AC2=DB2-DC2,求证:AD⊥BC.
则a=e+c,b=e+d,
所以a2-b2=(e+c)2-(e+d)2=c2+2e·c-2e·d-d2,
由条件知,a2=c2-d2+b2,
所以AD⊥BC.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0).
(1)求F1,F2分别对质点所做的功;
=3×(-13)+4×(-15)=-99(J),
=6×(-13)+(-5)×(-15)=-3(J).
∴力F1,F2对质点所做的功分别为-99 J和-3 J.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求F1,F2的合力F对质点所做的功.
=[(3,4)+(6,-5)]·(-13,-15)
=(9,-1)·(-13,-15)
=9×(-13)+(-1)×(-15)
=-117+15=-102(J).
∴合力F对质点所做的功为-102 J.
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立如图所示的直角坐标系.
所以2×4+(-a)·a=0,即a2=8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.若点M是△ABC所在平面内的一点,且满足 =0,则△ABM与△ABC的面积之比为
A.1∶2 B.1∶3
C.1∶4 D.2∶5
√
解析 如图,D为BC边的中点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.用两条成120°角的等长的绳子悬挂一个灯具,如图所示,已知灯具重10 N,则每根绳子的拉力大小为_____ N.
10
解析 设重力为G,每根绳的拉力分别为F1,F2,
则由题意得F1,F2与-G都成60°角,
且|F1|=|F2|,F1+F2+G=0.
∴|F1|=|F2|=|G|=10 N,
∴每根绳子的拉力都为10 N.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
A.垂心 B.内心 C.外心 D.重心
√
所以动点M在线段BC的中垂线上,
所以动点M形成的图形必通过△ABC的外心,选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.一艘船从南岸出发,向北岸横渡.根据测量,这一天水流速度为3 km/h,方向正东,风吹向北偏西30°,受风力影响,静水中船的漂行速度为3 km/h,若要使该船由南向北沿垂直于河岸的方向以
2 km/h的速度横渡,求船本身的速度大小及方向.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 如图,设水的速度为v1,风的速度为v2,v1+v2=a.
可求得a的方向是北偏东30°,a的大小是3 km/h.
船本身的速度为v3,则a+v3=v,即v3=v-a,
本课结束
6.4.1 平面几何中的向量方法
6.4.2 向量在物理中的应用举例
学习目标
XUE XI MU BIAO
1.能用向量方法解决简单的几何问题.
2.能用向量方法解决简单的力学问题和其他实际问题.
3.体会向量在解决数学和实际问题中的作用,培养学生的运算、
分析和解决实际问题的能力.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
用向量方法解决平面几何问题的“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为 问题.
(2)通过 ,研究几何元素之间的关系,如距离、夹角等问题.
(3)把运算结果“ ”成几何关系.
知识点一 向量方法解决平面几何问题的步骤
向量
向量运算
翻译
(1)物理问题中常见的向量有 等.
(2)向量的加减法运算体现在 .
(3)动量mv是向量的 运算.
(4)功是 与 的数量积.
知识点二 向量在物理中的应用
力、速度、加速度、位移
力、速度、加速度、位移的合成与分解
数乘
力F
所产生的位移s
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.若△ABC为直角三角形,则有 =0.( )
2.若向量 ,则AB∥CD.( )
3.功是力F与位移s的数量积.( )
4.力的合成与分解体现了向量的加减法运算.( )
√
×
√
×
2
题型探究
PART TWO
一、利用向量证明平面几何问题
例1 如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
则|a|=|b|,a·b=0.
方法二 如图所示,建立平面直角坐标系,设正方形的边长为2,则A(0,0),D(0,2),E(1,0),F(2,1),
=2-2=0,
反思感悟
用向量证明平面几何问题的两种基本思路
(1)向量的线性运算法的四个步骤:
①选取基底;
②用基底表示相关向量;
③利用向量的线性运算或数量积找到相应关系;
④把计算所得结果转化为几何问题.
(2)向量的坐标运算法的四个步骤:
①建立适当的平面直角坐标系;
②把相关向量坐标化;
③利用向量的坐标运算找到相应关系;
④利用向量关系回答几何问题.
跟踪训练1 如图所示,在平行四边形ABCD中,BC=2BA,∠ABC=60°,作AE⊥BD交BC于点E,求BE∶EC.
即(λb-a)·(a+b)=0,
方法二 以B为坐标原点,BC所在直线为x轴建立平面直角坐标系,设B(0,0),C(2,0),
二、利用平面向量求几何中的长度问题
例2 在平行四边形ABCD中,AD=1,AB=2,对角线BD=2,求对角线AC的长.
反思感悟
用向量法求长度的策略
(1)根据图形特点选择基底,利用向量的数量积转化,用公式|a|2=a2求解.
(2)建立坐标系,确定相应向量的坐标,代入公式:若a=(x,y),则|a|= .
跟踪训练2 在△ABC中,已知A(4,1),B(7,5),C(-4,7),则BC边上的中线AD的长是
√
三、向量在物理中的应用
例3 一条宽为 km的河,水流速度为2 km/h,在河两岸有两个码头A,B,已知AB= km,船在水中的最大航速为4 km/h,问该船怎样安排航行速度可使它从A码头最快到达彼岸B码头?用时多少?
以AC和AD为邻边作?ACED,且当AE与AB重合时能最快到达彼岸,
根据题意知AC⊥AE,在Rt△ADE和?ACED中,
∴∠EAD=30°.
答 该船实际航行速度大小为4 km/h,与水流方向成120°角时能最快到达B码头,用时0.5 h.
反思感悟
用向量解决物理问题的一般步骤
(1)问题的转化,即把物理问题转化为数学问题.
(2)模型的建立,即建立以向量为主体的数学模型.
(3)参数的获得,即求出数学模型的有关解——理论参数值.
(4)问题的答案,即回到问题的初始状态,解释相关的物理现象.
跟踪训练3 一物体在力F1=(3,-4),F2=(2,-5),F3=(3,1)的共同作用下从点A(1,1)移动到点B(0,5).在这个过程中三个力的合力所做的功为________.
-40
解析 ∵F1=(3,-4),F2=(2,-5),F3=(3,1),
∴合力F=F1+F2+F3=(8,-8).
即三个力的合力做的功等于-40.
核心素养之逻辑推理、数学建模
HE XIN SU YANG ZHI LUO JI TUI LI SHU XUE JIAN MO
平面几何中的平行(或共线)问题
典例 如图,点O是平行四边形ABCD的中心,E,F分别在边CD,
AB上,且
求证:点E,O,F在同一直线上.
知E,F分别是CD,AB的三等分点,
故点E,O,F在同一直线上.
素养提升
(1)利用向量方法可以解决平面几何中的平行(共线)等问题,有两种思路:一种思路是选择一组基底,利用基向量表示涉及的向量,另一种思路是建立坐标系,求出题目中涉及的向量的坐标.
(2)通过用向量方法解决平面几何问题,培养数学建模、逻辑推理素养.
3
随堂演练
PART THREE
1.人骑自行车的速度是v1,风速为v2,则逆风行驶的速度为
A.v1-v2 B.v1+v2
C.|v1|-|v2| D.
√
1
2
3
4
5
解析 由向量的加法法则可得逆风行驶的速度为v1+v2.
注意速度是有方向和大小的,是一个向量.故选B.
A.是正三角形 B.是直角三角形
C.是等腰三角形 D.形状无法确定
√
∴CA=CB,则△ABC是等腰三角形.
1
2
3
4
5
3.已知A,B,C,D四点的坐标分别为(1,0),(4,3),(2,4),(0,2),则此四边形为
A.梯形 B.菱形
C.矩形 D.正方形
√
1
2
3
4
5
4.当两人提起重量为|G|的旅行包时,两人用力方向的夹角为θ,用力大小都为|F|,若|F|=|G|,则θ的值为
A.30° B.60° C.90° D.120°
√
当|F1|=|F2|=|G|时,△OAC为正三角形,
所以∠AOC=60°,从而∠AOB=120°.
1
2
3
4
5
1
2
3
4
5
=______.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)平面几何中的向量方法.
(2)向量在物理中的应用.
2.方法归纳:化归转化、数形结合.
3.常见误区:要注意选择恰当的基底.
4
课时对点练
PART FOUR
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.已知力F的大小|F|=10,在F的作用下产生的位移s的大小|s|=14,F与s的夹角为60°,则F做的功为
A.7 B.10
C.14 D.70
√
2.已知点A(-2,-3),B(19,4),C(-1,-6),则△ABC是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
∴△ABC为直角三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(多选)关于船从两平行河岸的一岸驶向另一岸所用的时间,正确的是
A.船垂直到达对岸所用时间最少
B.当船速v的方向与河岸垂直时用时最少
C.沿任意直线运动到达对岸的时间都一样
D.船垂直到达对岸时航行的距离最短
√
√
解析 根据向量将船速v分解,当v垂直河岸时,用时最少.
船垂直到达对岸时航行的距离最短.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.三个内角的角平分线的交点
B.三条边的垂直平分线的交点
C.三条中线的交点
D.三条高所在直线的交点
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
同理OA⊥BC,OC⊥AB,
∴O为三条高所在直线的交点.
√
∴四边形ABCD的面积
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
∴AP为Rt△ABC斜边BC的中线.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.一条河宽为8 000 m,一船从A处出发垂直航行到达河正对岸的B处,船速为20 km/h,水速为12 km/h,则船到达B处所需时间为_____ h.
0.5
解析 如图,v实际=v船+v水=v1+v2,
|v1|=20,|v2|=12,
∴该船到达B处所需的时间为0.5 h.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,以A为坐标原点,以AB所在直线为x轴,以AD所在直线为y轴建立平面直角坐标系,
则A(0,0),B(2,0),D(0,1),∴C(2,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.如图所示,若D是△ABC内的一点,且AB2-AC2=DB2-DC2,求证:AD⊥BC.
则a=e+c,b=e+d,
所以a2-b2=(e+c)2-(e+d)2=c2+2e·c-2e·d-d2,
由条件知,a2=c2-d2+b2,
所以AD⊥BC.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0).
(1)求F1,F2分别对质点所做的功;
=3×(-13)+4×(-15)=-99(J),
=6×(-13)+(-5)×(-15)=-3(J).
∴力F1,F2对质点所做的功分别为-99 J和-3 J.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求F1,F2的合力F对质点所做的功.
=[(3,4)+(6,-5)]·(-13,-15)
=(9,-1)·(-13,-15)
=9×(-13)+(-1)×(-15)
=-117+15=-102(J).
∴合力F对质点所做的功为-102 J.
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立如图所示的直角坐标系.
所以2×4+(-a)·a=0,即a2=8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.若点M是△ABC所在平面内的一点,且满足 =0,则△ABM与△ABC的面积之比为
A.1∶2 B.1∶3
C.1∶4 D.2∶5
√
解析 如图,D为BC边的中点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.用两条成120°角的等长的绳子悬挂一个灯具,如图所示,已知灯具重10 N,则每根绳子的拉力大小为_____ N.
10
解析 设重力为G,每根绳的拉力分别为F1,F2,
则由题意得F1,F2与-G都成60°角,
且|F1|=|F2|,F1+F2+G=0.
∴|F1|=|F2|=|G|=10 N,
∴每根绳子的拉力都为10 N.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
A.垂心 B.内心 C.外心 D.重心
√
所以动点M在线段BC的中垂线上,
所以动点M形成的图形必通过△ABC的外心,选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.一艘船从南岸出发,向北岸横渡.根据测量,这一天水流速度为3 km/h,方向正东,风吹向北偏西30°,受风力影响,静水中船的漂行速度为3 km/h,若要使该船由南向北沿垂直于河岸的方向以
2 km/h的速度横渡,求船本身的速度大小及方向.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 如图,设水的速度为v1,风的速度为v2,v1+v2=a.
可求得a的方向是北偏东30°,a的大小是3 km/h.
船本身的速度为v3,则a+v3=v,即v3=v-a,
本课结束
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
