6.4.3 第4课时 余弦定理、正弦定理应用举例课件(共65张PPT)2020-2021学年高一下学期数学人教A版(2019)必修第二册第六章
文档属性
| 名称 | 6.4.3 第4课时 余弦定理、正弦定理应用举例课件(共65张PPT)2020-2021学年高一下学期数学人教A版(2019)必修第二册第六章 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 20:23:07 | ||
图片预览









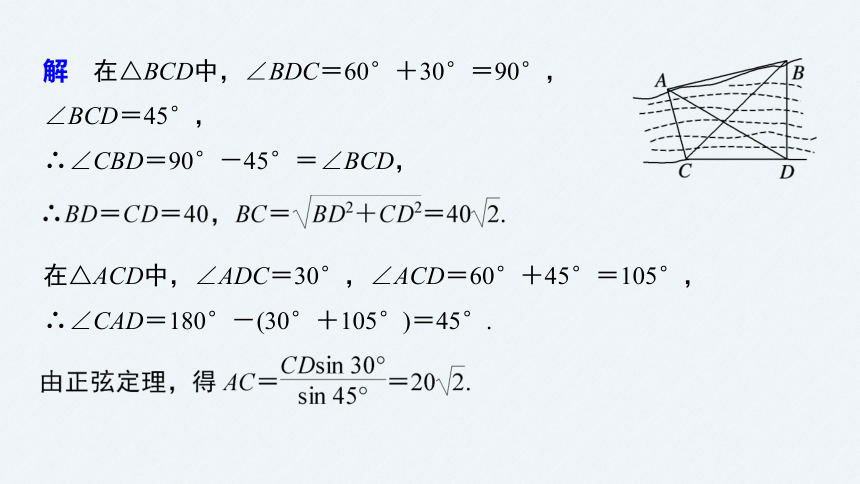

文档简介
第六章 6.4.3 余弦定理、正弦定理
第4课时 余弦定理、正弦定理应用举例
学习目标
XUE XI MU BIAO
1.会用正弦定理、余弦定理解决生产实践中有关距离、高度、
角度的测量问题.
2.培养提出问题、正确分析问题、独立解决问题的能力.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 基线的概念与选择原则
1.定义
在测量过程中,我们把根据测量的需要而确定的 叫做基线.
2.性质
在测量过程中,应根据实际需要选取合适的 ,使测量具有较高的精确度.一般来说,基线越长,测量的精确度越 .
线段
基线长度
高
知识点二 测量中的有关角的概念
1.仰角和俯角
在同一铅垂平面内的水平线和目标视线的夹角,目标视线在水平线上方时叫 ,目标视线在水平线下方时叫 .(如图所示)
2.方向角
从指定方向线到目标方向线所成的水平角.如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°. (如图所示)
仰角
俯角
思考 李尧出校向南前进了200米,再向东走了200米,回到自己家中,你认为李尧的家在学校的哪个方向?
答案 东南方向.
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.仰角是视线与视线在水平面的射影的夹角.( )
2.两点间不可到达又不可视问题的测量方案实质是构造已知两边及夹角的三角形并求解.( )
3.两点间可视但不可到达问题的测量方案实质是构造已知两角及一边的三角形并求解.( )
4.高度问题大多通过正(余)弦定理构造直角三角形来解决.( )
√
√
√
√
2
题型探究
PART TWO
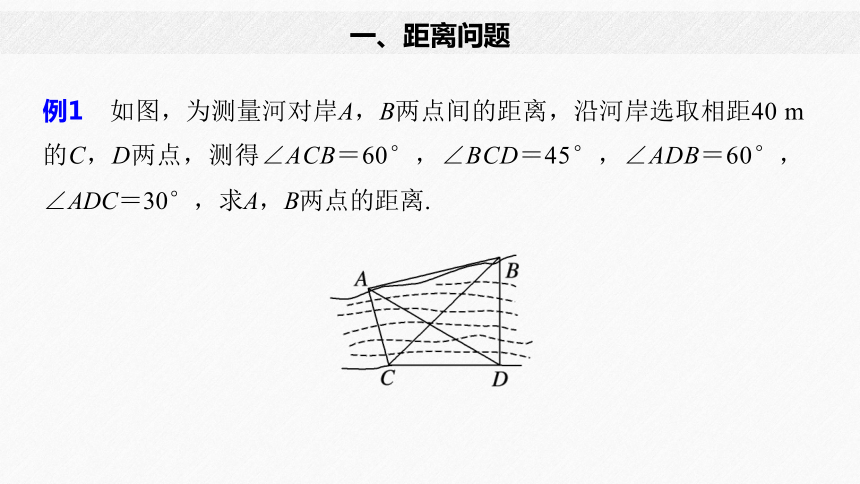
例1 如图,为测量河对岸A,B两点间的距离,沿河岸选取相距40 m的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,求A,B两点的距离.
一、距离问题
解 在△BCD中,∠BDC=60°+30°=90°,∠BCD=45°,
∴∠CBD=90°-45°=∠BCD,
在△ACD中,∠ADC=30°,∠ACD=60°+45°=105°,
∴∠CAD=180°-(30°+105°)=45°.
反思感悟
求两个不可到达的点之间的距离问题,一般是把问题转化为求三角形的边长问题,基本方法是
(1)认真理解题意,正确作出图形,根据条件和图形特点寻找可解的三角形.
(2)把实际问题里的条件和所求转换成三角形中的已知和未知的边和角,利用正、余弦定理求解.
跟踪训练1 (1)A,B两地之间隔着一个山岗,如图,现选择另一点C,测得CA=7 km,CB=5 km,C=60°,则A,B两点之间的距离为______ km.
解析 由余弦定理,
得AB2=CA2+CB2-2CA·CB·cos C
=39.
(2)如图,为了测量河的宽度,在一岸边选定两点A,B,望对岸的标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m,则河的宽度是_____ m.
60
又AD+DB=120,
∴AD·tan 30°=(120-AD)·tan 75°,
即河的宽度是60 m.
二、高度问题
例2 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高是
√
解析 在△BCD中,CD=10 m,∠BDC=45°,
∠BCD=15°+90°=105°,∠DBC=30°,
反思感悟
测量高度问题的解题策略
(1)“空间”向“平面”的转化:测量高度问题往往是空间中的问题,因此先要选好所求线段所在的平面,将空间问题转化为平面问题.
(2)“解直角三角形”与“解非直角三角形”结合,全面分析所有三角形,仔细规划解题思路.
跟踪训练2 珠穆朗玛峰是印度洋板块和欧亚板块碰撞挤压形成的.这种挤压一直在进行,珠穆朗玛峰的高度也一直在变化.由于地势险峻,气候恶劣,通常采用人工攀登的方式为珠峰“量身高”.攀登者们肩负高精度测量仪器,采用了分段测量的方法,从山脚开始,直到到达山顶,再把所有的高度差累加,就会得到珠峰的高度.2020年5月,中国珠峰高程测量登山队8名队员开始新一轮的珠峰测量工作.在测量
过程中,已知竖立在B点处的测量觇标高10米,攀登
者们在A处测得到觇标底点B和顶点C的仰角分别为
70°,80°,则A,B的高度差约为
A.10米 B.9.72米
C.9.40米 D.8.62米
√
解析 根据题意画出如图的模型,
则CB=10,∠OAB=70°,∠OAC=80°,
所以∠CAB=10°,∠ACB=10°,
所以AB=10,
所以在Rt△AOB中,BO=10sin 70°≈9.4(米).
三、角度问题
例3 甲船在A点发现乙船在北偏东60°的B处,乙船以每小时a海里的速度向北行驶,已知甲船的速度是每小时 a海里,问甲船应沿着什么方向前进,才能最快与乙船相遇?
解 如图所示.
设经过t小时两船在C点相遇,
B=180°-60°=120°,
∵0°<∠CAB<60°,∴∠CAB=30°,
∴∠DAC=60°-30°=30°,
∴甲船应沿着北偏东30°的方向前进,才能最快与乙船相遇.
反思感悟
测量角度问题的基本思路
测量角度问题的关键是在弄清题意的基础上,画出表示实际问题的图形,并在图形中标出有关的角和距离,再用正弦定理或余弦定理解三角形,最后将解得的结果转化为实际问题的解.
跟踪训练3 地图测绘人员在点A测得某一目标参照物P在他的北偏东30°的方向,且距离为40 m,之后该测绘人员沿正北方向行走了40 m,到达点B.试确定此时目标参照物P在他北偏东的度数以及他与目标参照物P的距离.
因为AB=40 m,所以AB=PB,
所以∠APB=∠PAB=30°,
所以∠PBA=120°.
因此测绘人员到达点B时,目标参照物P在他的北偏东60°方向上,
且目标参照物P与他的距离为40 m.
3
随堂演练
PART THREE
1.如图所示,设A,B两点在河的两岸,一测量者与A在河的同侧,在所在的河岸边先确定一点C,测出A,C的距离为50 m,∠ACB=45°,∠CAB=105°后,可以计算出A,B两点的距离为
√
解析 ∠ABC=180°-45°-105°=30°,
1
2
3
4
5
2.若点A在点C的北偏东30°方向上,点B在点C的南偏东60°方向上,且AC=BC,则点A在点B的
A.北偏东15°方向上 B.北偏西15°方向上
C.北偏东10°方向上 D.北偏西10°方向上
√
解析 如图所示,∠ACB=90°.
又因为AC=BC,
所以∠CBA=45°.
因为β=30°,所以α=90°-45°-30°=15°.
所以点A在点B的北偏西15°方向上.
1
2
3
4
5
3.如图,要测出山上一座天文台BC的高,从山腰A处测得AC=60 m,天文台最高处B的仰角为45°,天文台底部C的仰角为15°,则天文台BC的高为
√
解析 由题图,可得B=45°,∠BAC=30°,
1
2
3
4
5
4.甲骑电动车以24 km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15 min后到点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是
√
解析 由题意知,AB=24× =6(km),∠BAS=30°,∠ASB=75°-30°=45°.
1
2
3
4
5
5.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡度为θ,则cos θ等于
1
2
3
4
5
√
1
2
3
4
5
课堂小结
KE TANG XIAO JIE
1.知识清单:不可到达的距离、高度、角度等实际问题的测量方案.
2.方法归纳:数形结合.
3.常见误区:方位角是易错点.
4
课时对点练
PART FOUR
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.已知海上A,B两个小岛相距10海里,C岛临近陆地,若从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B岛与C岛之间的距离是
√
解析 如图所示,C=180°-60°-75°=45°,AB=10 (海里).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(多选)某人向正东方向走了x km后向右转了150°,然后沿新方向走了3 km,结果离出发点恰好 km,则x的值为
√
√
解析 如图所示,在△ABC中,AB=x,BC=3,AC= ,∠ABC=30°,
由余弦定理得,AC2=AB2+BC2-2AB·BC·cos∠ABC.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.一艘船向正北方向航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°方向上,另一灯塔在船的南偏西75°方向上,则这艘船的速度是
A.5 海里/时 B.5海里/时
C.10 海里/时 D.10海里/时
√
解析 如图,依题意有∠BAC=60°,∠BAD=75°,
所以∠CAD=∠CDA=15°,从而CD=CA=10(海里),
在Rt△ABC中,由正弦定理,可得AB=5(海里),
所以这艘船的速度是10海里/时.故选D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.从高出海平面h米的小岛上看正东方向有一只船俯角为30°,看正南方向一只船俯角为45°,则此时两船间的距离为
√
即此时两船间的距离为2h米.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.如图所示,为测一建筑物的高度,在地面上选取A,B两点,从A,B两点测得建筑物顶端的仰角分别为30°,45°,且A,B两点间的距离为60 m,则该建筑物的高度为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 在△PAB中,∠PAB=30°,∠APB=15°,AB=60 m,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.一角槽的横断面如图所示,四边形ABED是矩形,已知∠DAC=50°,∠CBE=70°,AC=90,BC=150,则DE=______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
210
解析 由题意知∠ACB=120°,在△ACB中,
由余弦定理,得AB2=AC2+BC2-2AC·BC·cos∠ACB=902+1502
-2×90×150× =44 100.
∴AB=210,DE=210.
7.如图,为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,A,B,C,D四点共圆,则AC的长为____ km.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为A,B,C,D四点共圆,
所以D+B=π.
在△ABC和△ADC中,
由余弦定理,可得82+52-2×8×5×cos(π-D)
故AC=7(km),即AC的长为7 km.
8.一艘船以每小时15 km的速度向东航行,船在A处看到一个灯塔B在北偏东60°方向上,行驶4 h后,船到达C处,看到这个灯塔在北偏东15°方向上,这时船与灯塔间的距离为_______ km.
解析 如图所示,在△ABC中,∠BAC=30°,∠ACB=105°,
则∠ABC=45°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6 n mile,渔船乙以5 n mile/h的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2 h追上.
(1)求渔船甲的速度;
解 依题意,知∠BAC=120°,AB=6,AC=5×2=10.
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB×AC×cos∠BAC=62+102-2×6×10×cos 120°=196,
所以渔船甲的速度为7 n mile/h.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求sin α.
解 在△ABC中,AB=6,∠BAC=120°,BC=14,∠BCA=α.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图,游客从某旅游景区的景点A处下山至C处有两种路径:一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.山路AC长为1 260 m,经测量,cos A= ,cos C= .
求索道AB的长.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
从而sin B=sin[π-(A+C)]=sin(A+C)
所以索道AB的长为1 040 m.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.(多选)如图所示,为了测量某湖泊两侧A,B间的距离,李宁同学首先选定了与A,B不共线的一点C,然后给出了三种测量方案(△ABC的角A,B,C所对的边分别记为a,b,c),则一定能确定A,B间距离的所有方案为
A.测量A,B,b B.测量a,b,C
C.测量A,B,a D.测量A,B,C
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 对于A,利用内角和定理先求出C=π-A-B,
对于B,直接利用余弦定理c2=a2+b2-2abcos C即可解出c;
对于C,先利用内角和定理求出C=π-A-B,
对于D,不知道长度,显然不能求c.
12.如图所示,D,C,B在地平面同一直线上,DC=10 m,从D,C两地测得A点的仰角分别为30°和45°,则A点离地面的高AB等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 方法一 设AB=x,则BC=x.
方法二 ∵∠ACB=45°,∠ADC=30°,
∴∠CAD=45°-30°=15°.
∴BD=10+x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.如图,两座相距60 m的建筑物AB,CD的高度分别为20 m,50 m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角为
A.30° B.45°
C.60° D.75°
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又CD=50,所以在△ACD中,
又0°<∠CAD<180°,
所以∠CAD=45°,
所以从顶端A看建筑物CD的张角为45°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°,沿点A向北偏东30°前进100 m 到达点B,在B点测得水柱顶端的仰角为30°,则水柱的高度是
A.50 m B.100 m
C.120 m D.150 m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 如图,设水柱的高度是h m,水柱底端为C,
即h2+50h-5 000=0,
即(h-50)(h+100)=0,
解得h=50或h=-100(舍去),故水柱的高度是50 m.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.在某次地震时,震中A(产生震动的中心位置)的南面有三座东西方向的城市B,C,D.已知B,C两市相距20 km,C,D两市相距34 km,C市在B,D两市之间,如图所示,某时刻C市感到地表震动,8 s后B市感到地表震动,20 s后D市感到地表震动,已知震波在地表传播的速度为每秒
1.5 km.,则震中A到B,C,D三市的距离分别为_________________________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意得,在△ABC中,
AB-AC=1.5×8=12(km).
在△ACD中,AD-AC=1.5×20=30(km).
设AC=x (km),
则AB=(12+x)(km),AD=(30+x)(km).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵B,C,D在一条直线上,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图,在海岸A处发现北偏东45°方向,距A处( -1)海里的B处有一艘走私船.在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以10 海里/时的速度追截走私船,此时走私船正以10海里/时的速度,从B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
解 设缉私船应沿CD方向行驶t小时,才能最快截获(在D点)走私船,
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·ACcos ∠BAC
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又0°<∠ABC<60°,∴∠ABC=45°,
∴B点在C点的正东方向上,
∴∠CBD=90°+30°=120°,
又∵0°<∠BCD<60°,∴∠BCD=30°,
∴缉私船沿北偏东60°的方向行驶.
又在△BCD中,∠CBD=120°,∠BCD=30°,
∴∠CDB=30°,∴BD=BC,
∴缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
第4课时 余弦定理、正弦定理应用举例
学习目标
XUE XI MU BIAO
1.会用正弦定理、余弦定理解决生产实践中有关距离、高度、
角度的测量问题.
2.培养提出问题、正确分析问题、独立解决问题的能力.
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 基线的概念与选择原则
1.定义
在测量过程中,我们把根据测量的需要而确定的 叫做基线.
2.性质
在测量过程中,应根据实际需要选取合适的 ,使测量具有较高的精确度.一般来说,基线越长,测量的精确度越 .
线段
基线长度
高
知识点二 测量中的有关角的概念
1.仰角和俯角
在同一铅垂平面内的水平线和目标视线的夹角,目标视线在水平线上方时叫 ,目标视线在水平线下方时叫 .(如图所示)
2.方向角
从指定方向线到目标方向线所成的水平角.如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°. (如图所示)
仰角
俯角
思考 李尧出校向南前进了200米,再向东走了200米,回到自己家中,你认为李尧的家在学校的哪个方向?
答案 东南方向.
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
1.仰角是视线与视线在水平面的射影的夹角.( )
2.两点间不可到达又不可视问题的测量方案实质是构造已知两边及夹角的三角形并求解.( )
3.两点间可视但不可到达问题的测量方案实质是构造已知两角及一边的三角形并求解.( )
4.高度问题大多通过正(余)弦定理构造直角三角形来解决.( )
√
√
√
√
2
题型探究
PART TWO
例1 如图,为测量河对岸A,B两点间的距离,沿河岸选取相距40 m的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,求A,B两点的距离.
一、距离问题
解 在△BCD中,∠BDC=60°+30°=90°,∠BCD=45°,
∴∠CBD=90°-45°=∠BCD,
在△ACD中,∠ADC=30°,∠ACD=60°+45°=105°,
∴∠CAD=180°-(30°+105°)=45°.
反思感悟
求两个不可到达的点之间的距离问题,一般是把问题转化为求三角形的边长问题,基本方法是
(1)认真理解题意,正确作出图形,根据条件和图形特点寻找可解的三角形.
(2)把实际问题里的条件和所求转换成三角形中的已知和未知的边和角,利用正、余弦定理求解.
跟踪训练1 (1)A,B两地之间隔着一个山岗,如图,现选择另一点C,测得CA=7 km,CB=5 km,C=60°,则A,B两点之间的距离为______ km.
解析 由余弦定理,
得AB2=CA2+CB2-2CA·CB·cos C
=39.
(2)如图,为了测量河的宽度,在一岸边选定两点A,B,望对岸的标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m,则河的宽度是_____ m.
60
又AD+DB=120,
∴AD·tan 30°=(120-AD)·tan 75°,
即河的宽度是60 m.
二、高度问题
例2 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高是
√
解析 在△BCD中,CD=10 m,∠BDC=45°,
∠BCD=15°+90°=105°,∠DBC=30°,
反思感悟
测量高度问题的解题策略
(1)“空间”向“平面”的转化:测量高度问题往往是空间中的问题,因此先要选好所求线段所在的平面,将空间问题转化为平面问题.
(2)“解直角三角形”与“解非直角三角形”结合,全面分析所有三角形,仔细规划解题思路.
跟踪训练2 珠穆朗玛峰是印度洋板块和欧亚板块碰撞挤压形成的.这种挤压一直在进行,珠穆朗玛峰的高度也一直在变化.由于地势险峻,气候恶劣,通常采用人工攀登的方式为珠峰“量身高”.攀登者们肩负高精度测量仪器,采用了分段测量的方法,从山脚开始,直到到达山顶,再把所有的高度差累加,就会得到珠峰的高度.2020年5月,中国珠峰高程测量登山队8名队员开始新一轮的珠峰测量工作.在测量
过程中,已知竖立在B点处的测量觇标高10米,攀登
者们在A处测得到觇标底点B和顶点C的仰角分别为
70°,80°,则A,B的高度差约为
A.10米 B.9.72米
C.9.40米 D.8.62米
√
解析 根据题意画出如图的模型,
则CB=10,∠OAB=70°,∠OAC=80°,
所以∠CAB=10°,∠ACB=10°,
所以AB=10,
所以在Rt△AOB中,BO=10sin 70°≈9.4(米).
三、角度问题
例3 甲船在A点发现乙船在北偏东60°的B处,乙船以每小时a海里的速度向北行驶,已知甲船的速度是每小时 a海里,问甲船应沿着什么方向前进,才能最快与乙船相遇?
解 如图所示.
设经过t小时两船在C点相遇,
B=180°-60°=120°,
∵0°<∠CAB<60°,∴∠CAB=30°,
∴∠DAC=60°-30°=30°,
∴甲船应沿着北偏东30°的方向前进,才能最快与乙船相遇.
反思感悟
测量角度问题的基本思路
测量角度问题的关键是在弄清题意的基础上,画出表示实际问题的图形,并在图形中标出有关的角和距离,再用正弦定理或余弦定理解三角形,最后将解得的结果转化为实际问题的解.
跟踪训练3 地图测绘人员在点A测得某一目标参照物P在他的北偏东30°的方向,且距离为40 m,之后该测绘人员沿正北方向行走了40 m,到达点B.试确定此时目标参照物P在他北偏东的度数以及他与目标参照物P的距离.
因为AB=40 m,所以AB=PB,
所以∠APB=∠PAB=30°,
所以∠PBA=120°.
因此测绘人员到达点B时,目标参照物P在他的北偏东60°方向上,
且目标参照物P与他的距离为40 m.
3
随堂演练
PART THREE
1.如图所示,设A,B两点在河的两岸,一测量者与A在河的同侧,在所在的河岸边先确定一点C,测出A,C的距离为50 m,∠ACB=45°,∠CAB=105°后,可以计算出A,B两点的距离为
√
解析 ∠ABC=180°-45°-105°=30°,
1
2
3
4
5
2.若点A在点C的北偏东30°方向上,点B在点C的南偏东60°方向上,且AC=BC,则点A在点B的
A.北偏东15°方向上 B.北偏西15°方向上
C.北偏东10°方向上 D.北偏西10°方向上
√
解析 如图所示,∠ACB=90°.
又因为AC=BC,
所以∠CBA=45°.
因为β=30°,所以α=90°-45°-30°=15°.
所以点A在点B的北偏西15°方向上.
1
2
3
4
5
3.如图,要测出山上一座天文台BC的高,从山腰A处测得AC=60 m,天文台最高处B的仰角为45°,天文台底部C的仰角为15°,则天文台BC的高为
√
解析 由题图,可得B=45°,∠BAC=30°,
1
2
3
4
5
4.甲骑电动车以24 km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15 min后到点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是
√
解析 由题意知,AB=24× =6(km),∠BAS=30°,∠ASB=75°-30°=45°.
1
2
3
4
5
5.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡度为θ,则cos θ等于
1
2
3
4
5
√
1
2
3
4
5
课堂小结
KE TANG XIAO JIE
1.知识清单:不可到达的距离、高度、角度等实际问题的测量方案.
2.方法归纳:数形结合.
3.常见误区:方位角是易错点.
4
课时对点练
PART FOUR
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.已知海上A,B两个小岛相距10海里,C岛临近陆地,若从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B岛与C岛之间的距离是
√
解析 如图所示,C=180°-60°-75°=45°,AB=10 (海里).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(多选)某人向正东方向走了x km后向右转了150°,然后沿新方向走了3 km,结果离出发点恰好 km,则x的值为
√
√
解析 如图所示,在△ABC中,AB=x,BC=3,AC= ,∠ABC=30°,
由余弦定理得,AC2=AB2+BC2-2AB·BC·cos∠ABC.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.一艘船向正北方向航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°方向上,另一灯塔在船的南偏西75°方向上,则这艘船的速度是
A.5 海里/时 B.5海里/时
C.10 海里/时 D.10海里/时
√
解析 如图,依题意有∠BAC=60°,∠BAD=75°,
所以∠CAD=∠CDA=15°,从而CD=CA=10(海里),
在Rt△ABC中,由正弦定理,可得AB=5(海里),
所以这艘船的速度是10海里/时.故选D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.从高出海平面h米的小岛上看正东方向有一只船俯角为30°,看正南方向一只船俯角为45°,则此时两船间的距离为
√
即此时两船间的距离为2h米.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.如图所示,为测一建筑物的高度,在地面上选取A,B两点,从A,B两点测得建筑物顶端的仰角分别为30°,45°,且A,B两点间的距离为60 m,则该建筑物的高度为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 在△PAB中,∠PAB=30°,∠APB=15°,AB=60 m,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.一角槽的横断面如图所示,四边形ABED是矩形,已知∠DAC=50°,∠CBE=70°,AC=90,BC=150,则DE=______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
210
解析 由题意知∠ACB=120°,在△ACB中,
由余弦定理,得AB2=AC2+BC2-2AC·BC·cos∠ACB=902+1502
-2×90×150× =44 100.
∴AB=210,DE=210.
7.如图,为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,A,B,C,D四点共圆,则AC的长为____ km.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为A,B,C,D四点共圆,
所以D+B=π.
在△ABC和△ADC中,
由余弦定理,可得82+52-2×8×5×cos(π-D)
故AC=7(km),即AC的长为7 km.
8.一艘船以每小时15 km的速度向东航行,船在A处看到一个灯塔B在北偏东60°方向上,行驶4 h后,船到达C处,看到这个灯塔在北偏东15°方向上,这时船与灯塔间的距离为_______ km.
解析 如图所示,在△ABC中,∠BAC=30°,∠ACB=105°,
则∠ABC=45°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6 n mile,渔船乙以5 n mile/h的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2 h追上.
(1)求渔船甲的速度;
解 依题意,知∠BAC=120°,AB=6,AC=5×2=10.
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB×AC×cos∠BAC=62+102-2×6×10×cos 120°=196,
所以渔船甲的速度为7 n mile/h.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求sin α.
解 在△ABC中,AB=6,∠BAC=120°,BC=14,∠BCA=α.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图,游客从某旅游景区的景点A处下山至C处有两种路径:一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.山路AC长为1 260 m,经测量,cos A= ,cos C= .
求索道AB的长.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
从而sin B=sin[π-(A+C)]=sin(A+C)
所以索道AB的长为1 040 m.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.(多选)如图所示,为了测量某湖泊两侧A,B间的距离,李宁同学首先选定了与A,B不共线的一点C,然后给出了三种测量方案(△ABC的角A,B,C所对的边分别记为a,b,c),则一定能确定A,B间距离的所有方案为
A.测量A,B,b B.测量a,b,C
C.测量A,B,a D.测量A,B,C
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 对于A,利用内角和定理先求出C=π-A-B,
对于B,直接利用余弦定理c2=a2+b2-2abcos C即可解出c;
对于C,先利用内角和定理求出C=π-A-B,
对于D,不知道长度,显然不能求c.
12.如图所示,D,C,B在地平面同一直线上,DC=10 m,从D,C两地测得A点的仰角分别为30°和45°,则A点离地面的高AB等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 方法一 设AB=x,则BC=x.
方法二 ∵∠ACB=45°,∠ADC=30°,
∴∠CAD=45°-30°=15°.
∴BD=10+x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.如图,两座相距60 m的建筑物AB,CD的高度分别为20 m,50 m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角为
A.30° B.45°
C.60° D.75°
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又CD=50,所以在△ACD中,
又0°<∠CAD<180°,
所以∠CAD=45°,
所以从顶端A看建筑物CD的张角为45°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°,沿点A向北偏东30°前进100 m 到达点B,在B点测得水柱顶端的仰角为30°,则水柱的高度是
A.50 m B.100 m
C.120 m D.150 m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 如图,设水柱的高度是h m,水柱底端为C,
即h2+50h-5 000=0,
即(h-50)(h+100)=0,
解得h=50或h=-100(舍去),故水柱的高度是50 m.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.在某次地震时,震中A(产生震动的中心位置)的南面有三座东西方向的城市B,C,D.已知B,C两市相距20 km,C,D两市相距34 km,C市在B,D两市之间,如图所示,某时刻C市感到地表震动,8 s后B市感到地表震动,20 s后D市感到地表震动,已知震波在地表传播的速度为每秒
1.5 km.,则震中A到B,C,D三市的距离分别为_________________________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意得,在△ABC中,
AB-AC=1.5×8=12(km).
在△ACD中,AD-AC=1.5×20=30(km).
设AC=x (km),
则AB=(12+x)(km),AD=(30+x)(km).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵B,C,D在一条直线上,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图,在海岸A处发现北偏东45°方向,距A处( -1)海里的B处有一艘走私船.在A处北偏西75°方向,距A处2海里的C处的我方缉私船奉命以10 海里/时的速度追截走私船,此时走私船正以10海里/时的速度,从B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
解 设缉私船应沿CD方向行驶t小时,才能最快截获(在D点)走私船,
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·ACcos ∠BAC
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又0°<∠ABC<60°,∴∠ABC=45°,
∴B点在C点的正东方向上,
∴∠CBD=90°+30°=120°,
又∵0°<∠BCD<60°,∴∠BCD=30°,
∴缉私船沿北偏东60°的方向行驶.
又在△BCD中,∠CBD=120°,∠BCD=30°,
∴∠CDB=30°,∴BD=BC,
∴缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
