苏科版 七下 7.4认识三角形同步课时训练试卷(word版含答案)
文档属性
| 名称 | 苏科版 七下 7.4认识三角形同步课时训练试卷(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 550.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览

文档简介
7.4认识三角形同步课时训练
一、单选题
1.长度分别为3,4,4,5的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.7 B.8 C.9 D.10
2.将一副三角板如图放置,其中,其中点D落在线段上,且,则的度数为( )
A. B. C. D.
3.如图,在ABC中,∠B+∠C=α,按图进行翻折,使,则∠FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
4.三角形的角平分线、中线和高都是 ( )
A.直线 B.线段 C.射线 D.以上答案都不对
5.将一副三角板如图放置,∠FDE=∠A=90°,∠C=45°,∠E=60°,且点D在BC上,点B在EF上,AC∥EF,则∠FDC的度数为( )
A.150° B.160° C.165° D.155°
6.如图,已知,,,,则( )
A.60° B.80° C.90° D.100°
7.小芳有长度分别为和的两根木条,桌上有下列长度的四根木条,她要用其中的一根与原有的两根木条钉成一个首尾相接的三角形木框,则这根木条的长度为( )
A. B. C. D.
8.如图,ABCD,BE交AD于点E,若∠B=18°,∠D=32°,则∠BED的度数为( )
A.18° B.32° C.50° D.60°
9.如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小5,则△ADE的面积为( )
A.5 B.4 C.3 D.2
10.如图,在折纸活动中,小明制作了一张纸片,点分别是边上的点,将沿着折叠压平,与重合,若,则( )
A. B. C. D.
二、填空题
11.如图,是两外角平分线的交点,是的两外角平分线的交点,,在上,又,在上;如果,那么__度.
12.在ABC中,∠A=∠B=∠C,则∠B=____度.
13.如图,直线,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=65°,则∠2的度数为_______.
14.如图,已知直线,直线,分别是截线,,,,分别平分,.则______.
15.如图,,点,分别在射线,上,平分,的反向延长线与的平分线交于点,则的度数是_______.
16.如图,若,点E在直线的上方,连接,延长交于点F,已知,,则_________°.
三、解答题
17.阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“梦想三角形”例如:一个三角形三个内角的度数分别是,,,这个三角形就是一个“梦想三角形”.反之,若一个三角形是“梦想三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
(1)如果一个“梦想三角形”有一个角为,那么这个“梦想三角形”的最小内角的度数为 .
(2)如图,已知,在射线上取一点,过点作交于点,以为端点作射线,交线段于点(点不与、重合),若,判定、是否是“梦想三角形”,为什么?
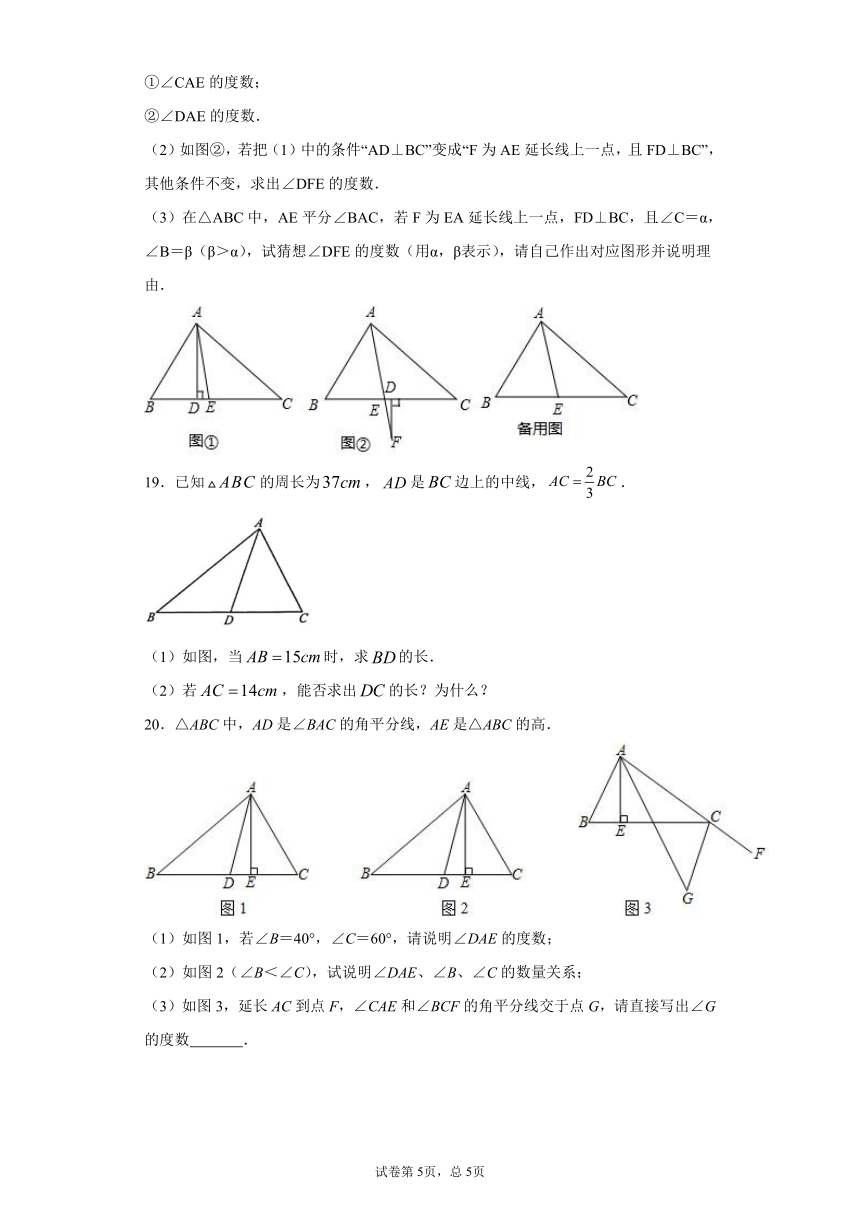
18.(1)如图①,△ABC中,点D、E在边BC上,AE平分∠BAC,AD⊥BC,∠C=40°,∠B=60°,求:
①∠CAE的度数;
②∠DAE的度数.
(2)如图②,若把(1)中的条件“AD⊥BC”变成“F为AE延长线上一点,且FD⊥BC”,其他条件不变,求出∠DFE的度数.
(3)在△ABC中,AE平分∠BAC,若F为EA延长线上一点,FD⊥BC,且∠C=α,∠B=β(β>α),试猜想∠DFE的度数(用α,β表示),请自己作出对应图形并说明理由.
19.已知的周长为,是边上的中线,.
(1)如图,当时,求的长.
(2)若,能否求出的长?为什么?
20.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=60°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,请直接写出∠G的度数 .
参考答案
1.A
2.D
3.D
4.B
5.C
6.C
7.B
8.C
9.A
10.B
11.66
12.60
13.
14.170°
15.
16.134
17.(1)或;(2),都是“梦想三角形”,理由见解析
【详解】
解:(1)当108°是三角形的一个内角的3倍,则有这个内角为36°,第三个内角也是36°,故最小的内角是36°,
当另外两个内角是3倍关系,则有另外两个内角分别为:54°,18°,最小的内角是18°
故答案为:36°或18°.
(2)结论:,都是“梦想三角形”
理由:,,
,
,
为“梦想三角形”,
,,,
,
,
“梦想三角形”.
18.(1)①40°;②10°;(2)10°;(3)∠DFE=(α﹣β),见解析
【详解】
解:(1)如图(1).
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣60°=30°,
∵∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣40°=80°,
而AE平分∠BAC,
∴∠CAE=∠BAE=∠BAC=×80°=40°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°;
(2)如图2中,作AH⊥BC于H.
由(1)可知∠HAE=10°,
∵AH∥EF,
∴∠DFE=∠HAE=10°
(3)结论:∠DFE=(∠B﹣∠C).理由如下:
如图3中,作AH⊥BC于H,FD⊥BC于D.
∵∠HAE=∠EAB﹣∠BAH,∠BAH=90°﹣∠B,∠BAE=(180°﹣∠B﹣∠C),
∴∠HAE=90°﹣∠B﹣∠C﹣(90°﹣∠B)
=(∠B﹣∠C),
∵AH∥FD,
∴∠DFE=∠HAE,
∴∠DFE=(α-β).
19.(1)6cm;(2)不能求出的长,理由见解析
【详解】
解:(1)∵,,
∴,
又∵的周长为,
∴,
∴,
又∵是边上的中线,
∴;
(2)不能,理由如下:
∵,,
∴,
又∵的周长为,
∴,
∴,
∴BC+AC=16∴不能构成三角形,故不能求出DC的长.
20.(1)∠DAE=10°;(2)∠DAE=∠C﹣∠B;(3)45°.
【详解】
解:(1)
是的高,
是的角平分线,
,
.
(2)
是的高,
是的角平分线,
,
即;
(3)和的角平分线交于点,
,即,
是的高,
,
.
故答案为:45°.
一、单选题
1.长度分别为3,4,4,5的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.7 B.8 C.9 D.10
2.将一副三角板如图放置,其中,其中点D落在线段上,且,则的度数为( )
A. B. C. D.
3.如图,在ABC中,∠B+∠C=α,按图进行翻折,使,则∠FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
4.三角形的角平分线、中线和高都是 ( )
A.直线 B.线段 C.射线 D.以上答案都不对
5.将一副三角板如图放置,∠FDE=∠A=90°,∠C=45°,∠E=60°,且点D在BC上,点B在EF上,AC∥EF,则∠FDC的度数为( )
A.150° B.160° C.165° D.155°
6.如图,已知,,,,则( )
A.60° B.80° C.90° D.100°
7.小芳有长度分别为和的两根木条,桌上有下列长度的四根木条,她要用其中的一根与原有的两根木条钉成一个首尾相接的三角形木框,则这根木条的长度为( )
A. B. C. D.
8.如图,ABCD,BE交AD于点E,若∠B=18°,∠D=32°,则∠BED的度数为( )
A.18° B.32° C.50° D.60°
9.如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小5,则△ADE的面积为( )
A.5 B.4 C.3 D.2
10.如图,在折纸活动中,小明制作了一张纸片,点分别是边上的点,将沿着折叠压平,与重合,若,则( )
A. B. C. D.
二、填空题
11.如图,是两外角平分线的交点,是的两外角平分线的交点,,在上,又,在上;如果,那么__度.
12.在ABC中,∠A=∠B=∠C,则∠B=____度.
13.如图,直线,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=65°,则∠2的度数为_______.
14.如图,已知直线,直线,分别是截线,,,,分别平分,.则______.
15.如图,,点,分别在射线,上,平分,的反向延长线与的平分线交于点,则的度数是_______.
16.如图,若,点E在直线的上方,连接,延长交于点F,已知,,则_________°.
三、解答题
17.阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“梦想三角形”例如:一个三角形三个内角的度数分别是,,,这个三角形就是一个“梦想三角形”.反之,若一个三角形是“梦想三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
(1)如果一个“梦想三角形”有一个角为,那么这个“梦想三角形”的最小内角的度数为 .
(2)如图,已知,在射线上取一点,过点作交于点,以为端点作射线,交线段于点(点不与、重合),若,判定、是否是“梦想三角形”,为什么?
18.(1)如图①,△ABC中,点D、E在边BC上,AE平分∠BAC,AD⊥BC,∠C=40°,∠B=60°,求:
①∠CAE的度数;
②∠DAE的度数.
(2)如图②,若把(1)中的条件“AD⊥BC”变成“F为AE延长线上一点,且FD⊥BC”,其他条件不变,求出∠DFE的度数.
(3)在△ABC中,AE平分∠BAC,若F为EA延长线上一点,FD⊥BC,且∠C=α,∠B=β(β>α),试猜想∠DFE的度数(用α,β表示),请自己作出对应图形并说明理由.
19.已知的周长为,是边上的中线,.
(1)如图,当时,求的长.
(2)若,能否求出的长?为什么?
20.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=60°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,请直接写出∠G的度数 .
参考答案
1.A
2.D
3.D
4.B
5.C
6.C
7.B
8.C
9.A
10.B
11.66
12.60
13.
14.170°
15.
16.134
17.(1)或;(2),都是“梦想三角形”,理由见解析
【详解】
解:(1)当108°是三角形的一个内角的3倍,则有这个内角为36°,第三个内角也是36°,故最小的内角是36°,
当另外两个内角是3倍关系,则有另外两个内角分别为:54°,18°,最小的内角是18°
故答案为:36°或18°.
(2)结论:,都是“梦想三角形”
理由:,,
,
,
为“梦想三角形”,
,,,
,
,
“梦想三角形”.
18.(1)①40°;②10°;(2)10°;(3)∠DFE=(α﹣β),见解析
【详解】
解:(1)如图(1).
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣60°=30°,
∵∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣40°=80°,
而AE平分∠BAC,
∴∠CAE=∠BAE=∠BAC=×80°=40°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°;
(2)如图2中,作AH⊥BC于H.
由(1)可知∠HAE=10°,
∵AH∥EF,
∴∠DFE=∠HAE=10°
(3)结论:∠DFE=(∠B﹣∠C).理由如下:
如图3中,作AH⊥BC于H,FD⊥BC于D.
∵∠HAE=∠EAB﹣∠BAH,∠BAH=90°﹣∠B,∠BAE=(180°﹣∠B﹣∠C),
∴∠HAE=90°﹣∠B﹣∠C﹣(90°﹣∠B)
=(∠B﹣∠C),
∵AH∥FD,
∴∠DFE=∠HAE,
∴∠DFE=(α-β).
19.(1)6cm;(2)不能求出的长,理由见解析
【详解】
解:(1)∵,,
∴,
又∵的周长为,
∴,
∴,
又∵是边上的中线,
∴;
(2)不能,理由如下:
∵,,
∴,
又∵的周长为,
∴,
∴,
∴BC+AC=16
20.(1)∠DAE=10°;(2)∠DAE=∠C﹣∠B;(3)45°.
【详解】
解:(1)
是的高,
是的角平分线,
,
.
(2)
是的高,
是的角平分线,
,
即;
(3)和的角平分线交于点,
,即,
是的高,
,
.
故答案为:45°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
