苏科版 八下 9.1图形的旋转同步课时训练试卷(word版含答案)
文档属性
| 名称 | 苏科版 八下 9.1图形的旋转同步课时训练试卷(word版含答案) | 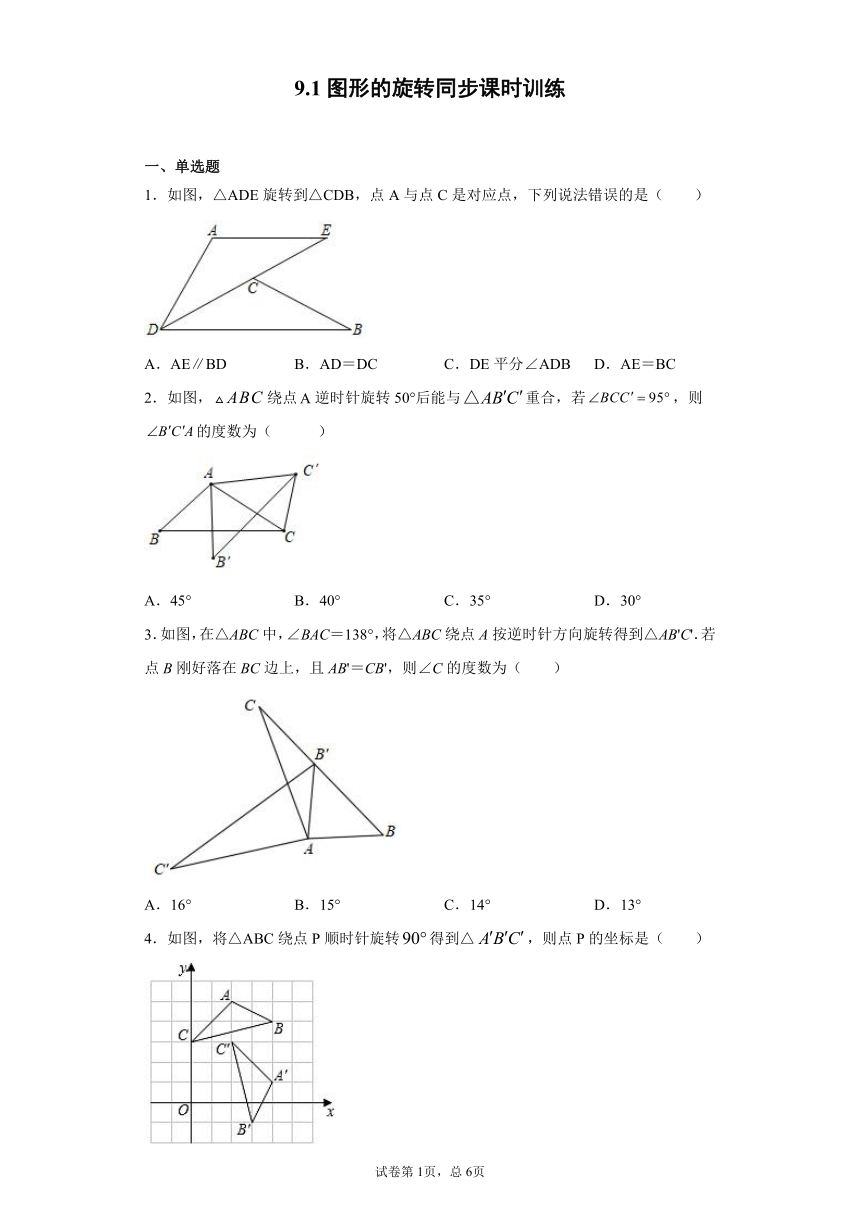 | |
| 格式 | docx | ||
| 文件大小 | 486.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 14:37:16 | ||
图片预览




文档简介
9.1图形的旋转同步课时训练
一、单选题
1.如图,△ADE旋转到△CDB,点A与点C是对应点,下列说法错误的是( )
A.AE∥BD B.AD=DC C.DE平分∠ADB D.AE=BC
2.如图,绕点逆时针旋转50°后能与重合,若,则的度数为( )
A.45° B.40° C.35° D.30°
3.如图,在△ABC中,∠BAC=138°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B刚好落在BC边上,且AB'=CB',则∠C的度数为( )
A.16° B.15° C.14° D.13°
4.如图,将△ABC绕点P顺时针旋转得到△,则点P的坐标是( )
A. B. C. D.
5.如图,已知OAB是正三角形,OP⊥OB,OP=OA,将OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到OPQ,则旋转的角度是( )
A.60° B.90° C.120° D.150°
6.如图,将等边三角形放在平面直角坐标系中,A点坐标,将绕点O逆时针旋转60°,则旋转后点B的对应点的坐标为( )
A. B. C. D.
7.如图,将△ABC绕着点B逆时针旋转45°后得到△A'BC′,若∠A=120°,∠C=35°,则∠A'BC的度数为( )
A.20° B.25° C.30° D.35°
8.将点绕原点顺时针旋转得到的点的坐标是( )
A. B. C. D.
9.将点绕原点顺时针旋转得到点的坐标为( )
A. B. C. D.
10.如图,在平面直角坐标系中,点的坐标分别为和,月牙绕点B旋转得到新的月牙,则点A的对应点的坐标是( )
A.或 B.或 C.或 D.或
二、填空题
11.如图,在中,,将绕着点顺时针旋转后,得到,且点在上,则的度数为__________.
12.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为__.
13.如图在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°),得到△A′B′C,设A′C交AB边于D,连结AA′,若△AA′D是等腰三角形,则旋转角α的度数为_____.
14.如图,在中,,,将绕点顺时针旋转至(点与点对应),连结,若,则的度数为______度.
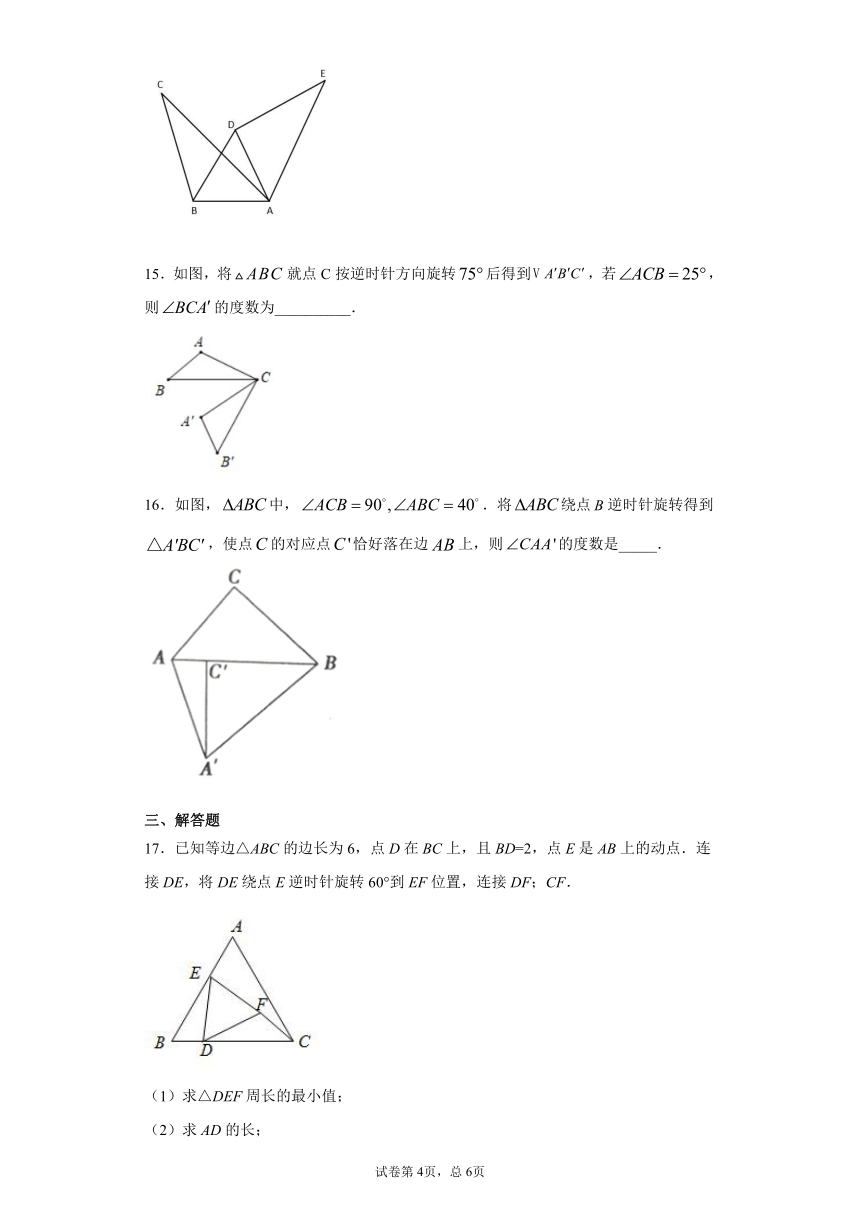
15.如图,将就点C按逆时针方向旋转后得到,若,则的度数为__________.
16.如图,中,.将绕点逆时针旋转得到,使点的对应点恰好落在边上,则的度数是_____.
三、解答题
17.已知等边△ABC的边长为6,点D在BC上,且BD=2,点E是AB上的动点.连接DE,将DE绕点E逆时针旋转60°到EF位置,连接DF;CF.
(1)求△DEF周长的最小值;
(2)求AD的长;
(3)当点E在AB运动时,△CDF的面积是否发生变化,若不变求出这个面积的值;若变化,请说明理由.
18.如图,是等边内的一点,且,,,将绕点逆时针旋转,得到.
(1)求点与点之间的距离;
(2)求的度数;
(3)求的面积.
19.在平面直角坐标系中,O为原点,点A(2,0),点B(0,2),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′.记旋转角为α.
(1)如图①,当点O′落在边AB上时,求点O′的坐标;
(2)如图②,当α=60°时,求AA′的长及点A′的坐标.
20.如图,在正方形中,请仅用无刻度直尺按下列要求作图(保留作图痕迹,不写作法).
(1)在图①中,将线段绕点逆时针旋转一定角度,使点与点重合,点与点重合,作出点的位置.
(2)在图②中,为的中点,将绕点逆时针旋转某个角度,得到,使与重合,作出.
参考答案
1.A
2.D
3.C
4.B
5.D
6.A
7.A
8.B
9.D
10.B
11.52°
12.24°
13.20°或40°
14.30
15.50°
16.120?
17.(1);(2)(或);(3)不变,
【详解】
解:(1)当DE⊥AB时DE最小,即△DEF周长最小,
由旋转的性质得,DE=EF,∠DEF=60°,
∴△DEF是等边三角形,
∴DE=EF=DF.
∵△ABC是等边三角形,
∴∠B=60°,
∴∠BDE=30°,
∴,
∴=,
∴△DEF周长的最小值为3;
(2)作AG⊥BC于G,
∵等边△ABC的边长为6,
∴,
∴DG=3-2=1,,
∴=(或);
(3)△CDF的面积不变化,作DM⊥AB于M,作FN⊥BC于N,
∵∠B=60°,
∴∠BDM=30°,
∵△DEF是等边三角形,
∴∠EDF=60°,
∴∠EDM+∠FDN=180°-30°-60°=90°,
∵∠DFN+∠FDN=90°,
∴∠EDM=∠DFN.
在△DEM和△FDN中
,
∴△DEM≌△FDN,
∴NF=DM,
由(1)可知,DM=,
∴NF=.
∵BC=6,BD=2,
∴CD=4,
∴.
18.(1);(2);(3).
【详解】
解:(1)如图1,连接,
∵绕点逆时针旋转得到,
∴,,
∴为等边三角形 ,
∴;
(2)∵绕点逆时针旋转得到,
∴,
∴
在中,∵,,,
∴,
∴ ,
∵,
∴ ;
(3)如图,作交于点,
∵为等边三角形,
∴,,
∴在中,,
∴ ,
同理:
将绕点逆时针旋转,得到,易得,
将绕点逆时针旋转,得到,易得,
.
19.(1)点O′的坐标为(,2﹣);(2)AA′=2,点A′的坐标为(1+,1+)
【详解】
解:(1)如图①,
∵点A(2,0),点B(0,2),
∴OA=OB=2,△ABO是等腰直角三角形,
∴AB=2,
当点O′落在边AB上时,α=45°,
∴点O′的横坐标为O′B=,纵坐标为2﹣,
∴点O′的坐标为(,2﹣);
(2)如图②,当α=60°时,
∴∠ABA′=60°,AB=A′B,
∴△ABA′为等边三角形,
∴AA′=A′B=AB=2,
连接OA′,
在△OBA′和△OAA′中,
,
∴△OBA′≌△OAA′(SSS),
∴∠BOA′=∠AOA′,∠BA′O=∠AA′O,
∴直线OA′的函数解析式为y=x,
∴OA′⊥AB,
∴OA′=+,
∴点A′的坐标为(1+ ,1+).
20.(1)如图所示,点即为所求.见解析;(2)如图所示,即为所求.见解析.
【详解】
(1)如图所示,点即为所求.
(2)如图所示,即为所求.
一、单选题
1.如图,△ADE旋转到△CDB,点A与点C是对应点,下列说法错误的是( )
A.AE∥BD B.AD=DC C.DE平分∠ADB D.AE=BC
2.如图,绕点逆时针旋转50°后能与重合,若,则的度数为( )
A.45° B.40° C.35° D.30°
3.如图,在△ABC中,∠BAC=138°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B刚好落在BC边上,且AB'=CB',则∠C的度数为( )
A.16° B.15° C.14° D.13°
4.如图,将△ABC绕点P顺时针旋转得到△,则点P的坐标是( )
A. B. C. D.
5.如图,已知OAB是正三角形,OP⊥OB,OP=OA,将OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到OPQ,则旋转的角度是( )
A.60° B.90° C.120° D.150°
6.如图,将等边三角形放在平面直角坐标系中,A点坐标,将绕点O逆时针旋转60°,则旋转后点B的对应点的坐标为( )
A. B. C. D.
7.如图,将△ABC绕着点B逆时针旋转45°后得到△A'BC′,若∠A=120°,∠C=35°,则∠A'BC的度数为( )
A.20° B.25° C.30° D.35°
8.将点绕原点顺时针旋转得到的点的坐标是( )
A. B. C. D.
9.将点绕原点顺时针旋转得到点的坐标为( )
A. B. C. D.
10.如图,在平面直角坐标系中,点的坐标分别为和,月牙绕点B旋转得到新的月牙,则点A的对应点的坐标是( )
A.或 B.或 C.或 D.或
二、填空题
11.如图,在中,,将绕着点顺时针旋转后,得到,且点在上,则的度数为__________.
12.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为__.
13.如图在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°),得到△A′B′C,设A′C交AB边于D,连结AA′,若△AA′D是等腰三角形,则旋转角α的度数为_____.
14.如图,在中,,,将绕点顺时针旋转至(点与点对应),连结,若,则的度数为______度.
15.如图,将就点C按逆时针方向旋转后得到,若,则的度数为__________.
16.如图,中,.将绕点逆时针旋转得到,使点的对应点恰好落在边上,则的度数是_____.
三、解答题
17.已知等边△ABC的边长为6,点D在BC上,且BD=2,点E是AB上的动点.连接DE,将DE绕点E逆时针旋转60°到EF位置,连接DF;CF.
(1)求△DEF周长的最小值;
(2)求AD的长;
(3)当点E在AB运动时,△CDF的面积是否发生变化,若不变求出这个面积的值;若变化,请说明理由.
18.如图,是等边内的一点,且,,,将绕点逆时针旋转,得到.
(1)求点与点之间的距离;
(2)求的度数;
(3)求的面积.
19.在平面直角坐标系中,O为原点,点A(2,0),点B(0,2),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′.记旋转角为α.
(1)如图①,当点O′落在边AB上时,求点O′的坐标;
(2)如图②,当α=60°时,求AA′的长及点A′的坐标.
20.如图,在正方形中,请仅用无刻度直尺按下列要求作图(保留作图痕迹,不写作法).
(1)在图①中,将线段绕点逆时针旋转一定角度,使点与点重合,点与点重合,作出点的位置.
(2)在图②中,为的中点,将绕点逆时针旋转某个角度,得到,使与重合,作出.
参考答案
1.A
2.D
3.C
4.B
5.D
6.A
7.A
8.B
9.D
10.B
11.52°
12.24°
13.20°或40°
14.30
15.50°
16.120?
17.(1);(2)(或);(3)不变,
【详解】
解:(1)当DE⊥AB时DE最小,即△DEF周长最小,
由旋转的性质得,DE=EF,∠DEF=60°,
∴△DEF是等边三角形,
∴DE=EF=DF.
∵△ABC是等边三角形,
∴∠B=60°,
∴∠BDE=30°,
∴,
∴=,
∴△DEF周长的最小值为3;
(2)作AG⊥BC于G,
∵等边△ABC的边长为6,
∴,
∴DG=3-2=1,,
∴=(或);
(3)△CDF的面积不变化,作DM⊥AB于M,作FN⊥BC于N,
∵∠B=60°,
∴∠BDM=30°,
∵△DEF是等边三角形,
∴∠EDF=60°,
∴∠EDM+∠FDN=180°-30°-60°=90°,
∵∠DFN+∠FDN=90°,
∴∠EDM=∠DFN.
在△DEM和△FDN中
,
∴△DEM≌△FDN,
∴NF=DM,
由(1)可知,DM=,
∴NF=.
∵BC=6,BD=2,
∴CD=4,
∴.
18.(1);(2);(3).
【详解】
解:(1)如图1,连接,
∵绕点逆时针旋转得到,
∴,,
∴为等边三角形 ,
∴;
(2)∵绕点逆时针旋转得到,
∴,
∴
在中,∵,,,
∴,
∴ ,
∵,
∴ ;
(3)如图,作交于点,
∵为等边三角形,
∴,,
∴在中,,
∴ ,
同理:
将绕点逆时针旋转,得到,易得,
将绕点逆时针旋转,得到,易得,
.
19.(1)点O′的坐标为(,2﹣);(2)AA′=2,点A′的坐标为(1+,1+)
【详解】
解:(1)如图①,
∵点A(2,0),点B(0,2),
∴OA=OB=2,△ABO是等腰直角三角形,
∴AB=2,
当点O′落在边AB上时,α=45°,
∴点O′的横坐标为O′B=,纵坐标为2﹣,
∴点O′的坐标为(,2﹣);
(2)如图②,当α=60°时,
∴∠ABA′=60°,AB=A′B,
∴△ABA′为等边三角形,
∴AA′=A′B=AB=2,
连接OA′,
在△OBA′和△OAA′中,
,
∴△OBA′≌△OAA′(SSS),
∴∠BOA′=∠AOA′,∠BA′O=∠AA′O,
∴直线OA′的函数解析式为y=x,
∴OA′⊥AB,
∴OA′=+,
∴点A′的坐标为(1+ ,1+).
20.(1)如图所示,点即为所求.见解析;(2)如图所示,即为所求.见解析.
【详解】
(1)如图所示,点即为所求.
(2)如图所示,即为所求.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
