苏科版 九下 6.7用位似三角形解决问题同步课时训练试卷(word版含答案)
文档属性
| 名称 | 苏科版 九下 6.7用位似三角形解决问题同步课时训练试卷(word版含答案) |

|
|
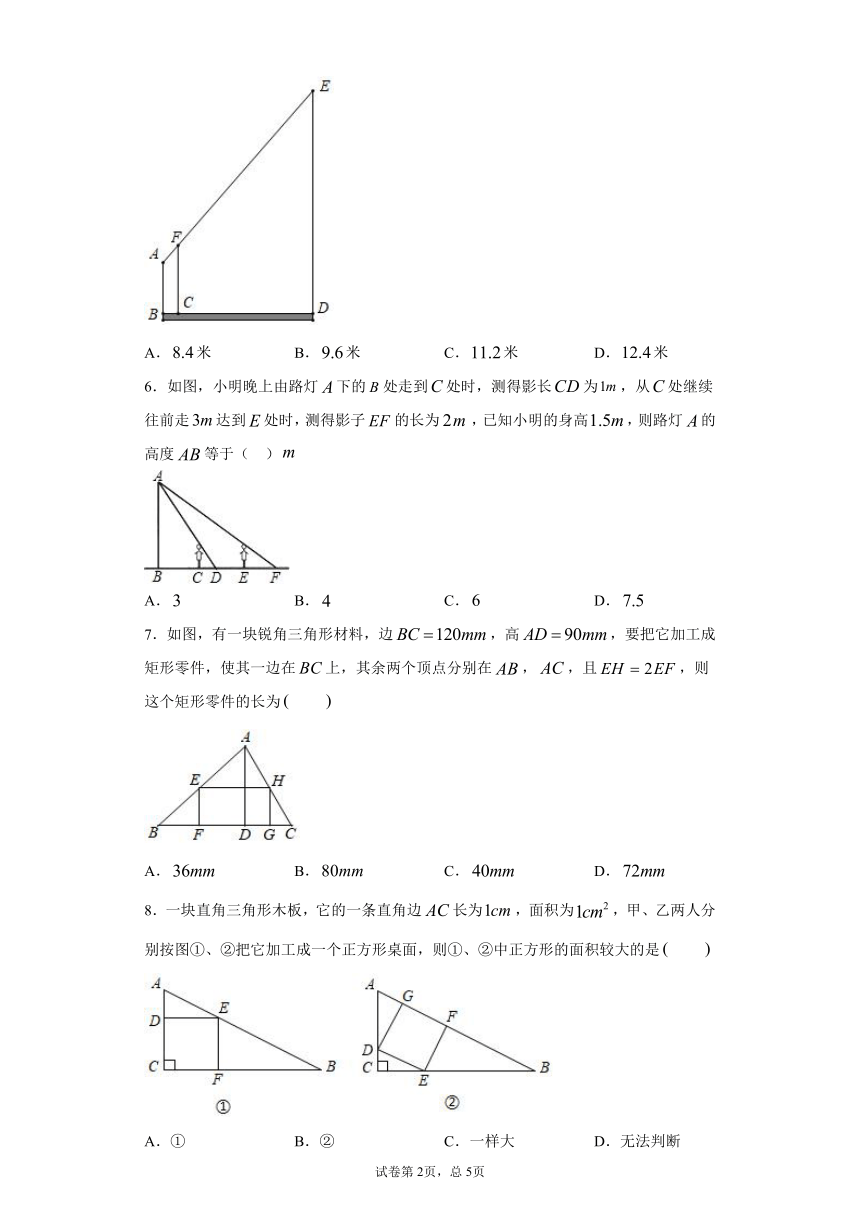
| 格式 | docx | ||
| 文件大小 | 312.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览


文档简介
6.7用位似三角形解决问题同步课时训练
一、单选题
1.如图是一块三角形钢材ABC,其中边,高,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
2.有一个三角形木架三边长分别是15cm,20cm,24cm,现要再做一个与其相似的三角形木架,而只有长为12cm和24cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
3.小明身高为1.6米,他在距路灯5米处的位置发现自己的影长为1米,他继续向前走,当他距离路灯为7米时,他的影长将( )
A.增长0.4米 B.减少0.4米 C.增长1.4米 D.减少1.4米
4.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,BC=7m,则建筑物CD的高是( )
A.3.5m B.4m C.4.5m D.5m
5.如图,某测量工作人员站在地面点B处利用标杆FC测量一旗杆ED的高度.测量人员眼睛处点A与标杆顶端处点F,旗杆顶端处点E在同一直线上,点B,C,D也在同一条直线上.已知此人眼睛到地面距离米,标杆高米,且米,米,则旗杆的高度为( )
A.米 B.米 C.米 D.米
6.如图,小明晚上由路灯下的处走到处时,测得影长为,从处继续往前走达到处时,测得影子的长为,已知小明的身高,则路灯的高度等于( )
A. B. C. D.
7.如图,有一块锐角三角形材料,边,高,要把它加工成矩形零件,使其一边在上,其余两个顶点分别在,,且,则这个矩形零件的长为
A. B. C. D.
8.一块直角三角形木板,它的一条直角边长为,面积为,甲、乙两人分别按图①、②把它加工成一个正方形桌面,则①、②中正方形的面积较大的是
A.① B.② C.一样大 D.无法判断
9.学校教学楼前面有一根高是4.2米的旗杆,在某时刻太阳光下的影子长是6.3米,与此同时, 在旗杆周边的一棵大树在地面上投影出的影子长是9米,则此大树的高度是( )
A.4.8米 B.8.4米 C.6米 D.9米
10.在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1米得竹竿的影长为3米,某高楼的影长为60米,那么高楼的高度是( )
A.1米 B.10米 C.20米 D.30米
二、填空题
11.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,AC=10m,则建筑物CD的高是_____m.
12.《九章算术》中记载了一种测量井深的方法.如图,在井口处立一根垂直于井口的木杆,从木杆的顶端观察井水水岸,视线与井口的直径交于点,如果测得米,米,米,那么井深为________米.
13.小明和他的同学在太阳下行走,小明身高米,他的影长为米,他同学的身高为米,则此时他的同学的影长为__________米.
14.如图,是斜靠在墙壁上的长梯,梯脚B到墙距离是1.6米梯上的点D到墙距离是1.4米,的长是0.55米,则梯子的长为__________米.
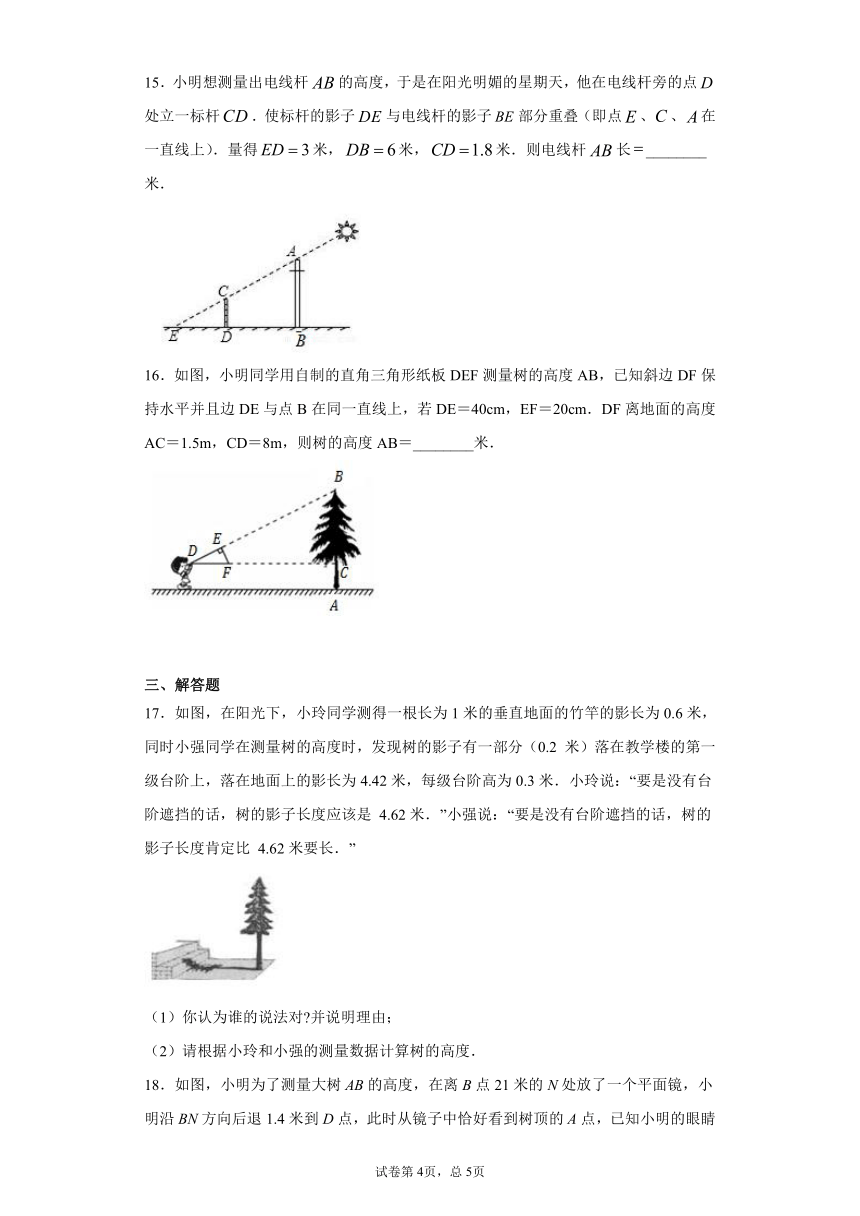
15.小明想测量出电线杆的高度,于是在阳光明媚的星期天,他在电线杆旁的点处立一标杆.使标杆的影子与电线杆的影子部分重叠(即点、、在一直线上).量得米,米,米.则电线杆长________米.
16.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,已知斜边DF保持水平并且边DE与点B在同一直线上,若DE=40cm,EF=20cm.DF离地面的高度AC=1.5m,CD=8m,则树的高度AB=________米.
三、解答题
17.如图,在阳光下,小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时小强同学在测量树的高度时,发现树的影子有一部分(0.2 米)落在教学楼的第一级台阶上,落在地面上的影长为4.42米,每级台阶高为0.3米.小玲说:“要是没有台阶遮挡的话,树的影子长度应该是 4.62米.”小强说:“要是没有台阶遮挡的话,树的影子长度肯定比 4.62米要长.”
(1)你认为谁的说法对?并说明理由;
(2)请根据小玲和小强的测量数据计算树的高度.
18.如图,小明为了测量大树AB的高度,在离B点21米的N处放了一个平面镜,小明沿BN方向后退1.4米到D点,此时从镜子中恰好看到树顶的A点,已知小明的眼睛(点C)到地面的高度CD是1.6米,求大树AB的高度.
19.如图,小明与同学合作利用太阳光线测量旗杆的高度,身高的小明()落在地面上的影长.
(1)请画出旗杆在同一时刻阳光照射下在地面上的影子.
(2)若小明测得此刻旗杆落在地面上的影长,求旗杆的高度.
20.在一次数学活动课上,王老师带领学生去测量教学楼的高度.在太阳光下,测得身高米的小同学(用线段表示)的影长为米,与此同时,测得教学楼(用线段表示)的影长为米.
(1)请你在图中画出影长;
(2)求教学楼的高度.
参考答案
1.B
2.B
3.A
4.D
5.C
6.C
7.D
8.A
9.C
10.C
11.5
12.6
13.2.
14.4.4
15.5.4
16.5.5
17.(1)小强的说法对,理由见解析;(2)8米.
【详解】
解:(1)小强的说法对;
根据题意画出图形,如图所示,
根据题意,得,
∵DE=0.3米,
∴(米).
∵GD∥FH,FG∥DH,
∴四边形DGFH是平行四边形,
∴米.
∵AE=4.42米,
∴AF=AE+EH+FH=4.42+0.18+0.2=4.8(米),
即要是没有台阶遮挡的话,树的影子长度是4.8米,
∴小强的说法对;
(2)由(1)可知:AF=4.8米.
∵,
∴米.
答:树的高度为8米.
18.24米
【详解】
解:∵AB⊥DB,DC⊥DB,
∴∠CDN=∠ABN=90°,
∵∠CND=∠ANB,
∴△CDN∽△ABN.
∴,
即,
∴AB=1.6×21÷1.4=24(米),
答:大树AB的高度为24米.
19.(1)见解析;(2)12m
【详解】
(1)如图;
(2)由题意可知:△ABC∽△DGE
∴,即
解得,
所以旗杆的长为12.
20.(1)见解析 (2)17.6米
【详解】
(1)画射线AC,过E点作EF∥AC,交AD于点F,
就是所求画影长.
(2)根据题意,∠EDF=∠CBA=90°,
∵EF∥AC,
∴∠EFD=∠CAB,
∴.
,
,
(米),
答:教学楼的高度为17.6米.
一、单选题
1.如图是一块三角形钢材ABC,其中边,高,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
2.有一个三角形木架三边长分别是15cm,20cm,24cm,现要再做一个与其相似的三角形木架,而只有长为12cm和24cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
3.小明身高为1.6米,他在距路灯5米处的位置发现自己的影长为1米,他继续向前走,当他距离路灯为7米时,他的影长将( )
A.增长0.4米 B.减少0.4米 C.增长1.4米 D.减少1.4米
4.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,BC=7m,则建筑物CD的高是( )
A.3.5m B.4m C.4.5m D.5m
5.如图,某测量工作人员站在地面点B处利用标杆FC测量一旗杆ED的高度.测量人员眼睛处点A与标杆顶端处点F,旗杆顶端处点E在同一直线上,点B,C,D也在同一条直线上.已知此人眼睛到地面距离米,标杆高米,且米,米,则旗杆的高度为( )
A.米 B.米 C.米 D.米
6.如图,小明晚上由路灯下的处走到处时,测得影长为,从处继续往前走达到处时,测得影子的长为,已知小明的身高,则路灯的高度等于( )
A. B. C. D.
7.如图,有一块锐角三角形材料,边,高,要把它加工成矩形零件,使其一边在上,其余两个顶点分别在,,且,则这个矩形零件的长为
A. B. C. D.
8.一块直角三角形木板,它的一条直角边长为,面积为,甲、乙两人分别按图①、②把它加工成一个正方形桌面,则①、②中正方形的面积较大的是
A.① B.② C.一样大 D.无法判断
9.学校教学楼前面有一根高是4.2米的旗杆,在某时刻太阳光下的影子长是6.3米,与此同时, 在旗杆周边的一棵大树在地面上投影出的影子长是9米,则此大树的高度是( )
A.4.8米 B.8.4米 C.6米 D.9米
10.在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1米得竹竿的影长为3米,某高楼的影长为60米,那么高楼的高度是( )
A.1米 B.10米 C.20米 D.30米
二、填空题
11.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,AC=10m,则建筑物CD的高是_____m.
12.《九章算术》中记载了一种测量井深的方法.如图,在井口处立一根垂直于井口的木杆,从木杆的顶端观察井水水岸,视线与井口的直径交于点,如果测得米,米,米,那么井深为________米.
13.小明和他的同学在太阳下行走,小明身高米,他的影长为米,他同学的身高为米,则此时他的同学的影长为__________米.
14.如图,是斜靠在墙壁上的长梯,梯脚B到墙距离是1.6米梯上的点D到墙距离是1.4米,的长是0.55米,则梯子的长为__________米.
15.小明想测量出电线杆的高度,于是在阳光明媚的星期天,他在电线杆旁的点处立一标杆.使标杆的影子与电线杆的影子部分重叠(即点、、在一直线上).量得米,米,米.则电线杆长________米.
16.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,已知斜边DF保持水平并且边DE与点B在同一直线上,若DE=40cm,EF=20cm.DF离地面的高度AC=1.5m,CD=8m,则树的高度AB=________米.
三、解答题
17.如图,在阳光下,小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时小强同学在测量树的高度时,发现树的影子有一部分(0.2 米)落在教学楼的第一级台阶上,落在地面上的影长为4.42米,每级台阶高为0.3米.小玲说:“要是没有台阶遮挡的话,树的影子长度应该是 4.62米.”小强说:“要是没有台阶遮挡的话,树的影子长度肯定比 4.62米要长.”
(1)你认为谁的说法对?并说明理由;
(2)请根据小玲和小强的测量数据计算树的高度.
18.如图,小明为了测量大树AB的高度,在离B点21米的N处放了一个平面镜,小明沿BN方向后退1.4米到D点,此时从镜子中恰好看到树顶的A点,已知小明的眼睛(点C)到地面的高度CD是1.6米,求大树AB的高度.
19.如图,小明与同学合作利用太阳光线测量旗杆的高度,身高的小明()落在地面上的影长.
(1)请画出旗杆在同一时刻阳光照射下在地面上的影子.
(2)若小明测得此刻旗杆落在地面上的影长,求旗杆的高度.
20.在一次数学活动课上,王老师带领学生去测量教学楼的高度.在太阳光下,测得身高米的小同学(用线段表示)的影长为米,与此同时,测得教学楼(用线段表示)的影长为米.
(1)请你在图中画出影长;
(2)求教学楼的高度.
参考答案
1.B
2.B
3.A
4.D
5.C
6.C
7.D
8.A
9.C
10.C
11.5
12.6
13.2.
14.4.4
15.5.4
16.5.5
17.(1)小强的说法对,理由见解析;(2)8米.
【详解】
解:(1)小强的说法对;
根据题意画出图形,如图所示,
根据题意,得,
∵DE=0.3米,
∴(米).
∵GD∥FH,FG∥DH,
∴四边形DGFH是平行四边形,
∴米.
∵AE=4.42米,
∴AF=AE+EH+FH=4.42+0.18+0.2=4.8(米),
即要是没有台阶遮挡的话,树的影子长度是4.8米,
∴小强的说法对;
(2)由(1)可知:AF=4.8米.
∵,
∴米.
答:树的高度为8米.
18.24米
【详解】
解:∵AB⊥DB,DC⊥DB,
∴∠CDN=∠ABN=90°,
∵∠CND=∠ANB,
∴△CDN∽△ABN.
∴,
即,
∴AB=1.6×21÷1.4=24(米),
答:大树AB的高度为24米.
19.(1)见解析;(2)12m
【详解】
(1)如图;
(2)由题意可知:△ABC∽△DGE
∴,即
解得,
所以旗杆的长为12.
20.(1)见解析 (2)17.6米
【详解】
(1)画射线AC,过E点作EF∥AC,交AD于点F,
就是所求画影长.
(2)根据题意,∠EDF=∠CBA=90°,
∵EF∥AC,
∴∠EFD=∠CAB,
∴.
,
,
(米),
答:教学楼的高度为17.6米.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
