苏科版七年级下11.3探索三角形全等的条件(4)教学案
文档属性
| 名称 | 苏科版七年级下11.3探索三角形全等的条件(4)教学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 56.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-02 15:31:57 | ||
图片预览

文档简介
11.3探索三角形全等的条件(4)
班级___________ 姓名___________学号___________
【学习目标】
⒈让学生进一步了解全等三角形在生活和生产中的应用,增强应用数学的意识;
⒉会用直尺和圆规作角平分线,并能有条理地说理和表达;
3.使学生掌握角平分线的性质和识别的方法,并会用解决有关简单问题.
【课前准备】
1、三角形全等的判定有哪几个?
2、如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,
③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有 ( )个. A.4 B.3 C.2 D.1
3.角平分线的定义: .
4.角平分线的性质: .
【探索新知】
小时候,我们都折过纸飞机,它的翼面如右图形状,你能说出它的特征吗?这样做有什么好处?
活动1.不利用任何工具,请你将一张用纸片做的角分成两个相等的角.你有什么方法?
活动2.如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
数学来源于生活,古代的能工巧匠就找到了解决的办法
如右图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB 、A沿着角的两边放下,沿AC画一条射线AE,则AE就是角平分线,你能说出其中的道理吗?
2. 工人师傅常常用角尺平分一个任意角,在∠COD的两边OC、OD上分别取OA=OB,移动角尺,使角的两边相同刻度分别与点A、B重合,这时过角尺顶点M的射线OM就是∠COD的平分线,请你说明这样画角平分线的道理.
【探究新知】
那么根据角平分仪的制作原理怎样作一个角的平分线?
画法 图形
1.以O为圆心,任意长为半径画弧,分别交射线OA、OB于点D、E2.分别以D、E为圆心,大于 DE的长度画弧,两弧在∠AOB的内部交于点C.3.画射线OC,OC就是∠AOB的角平分线
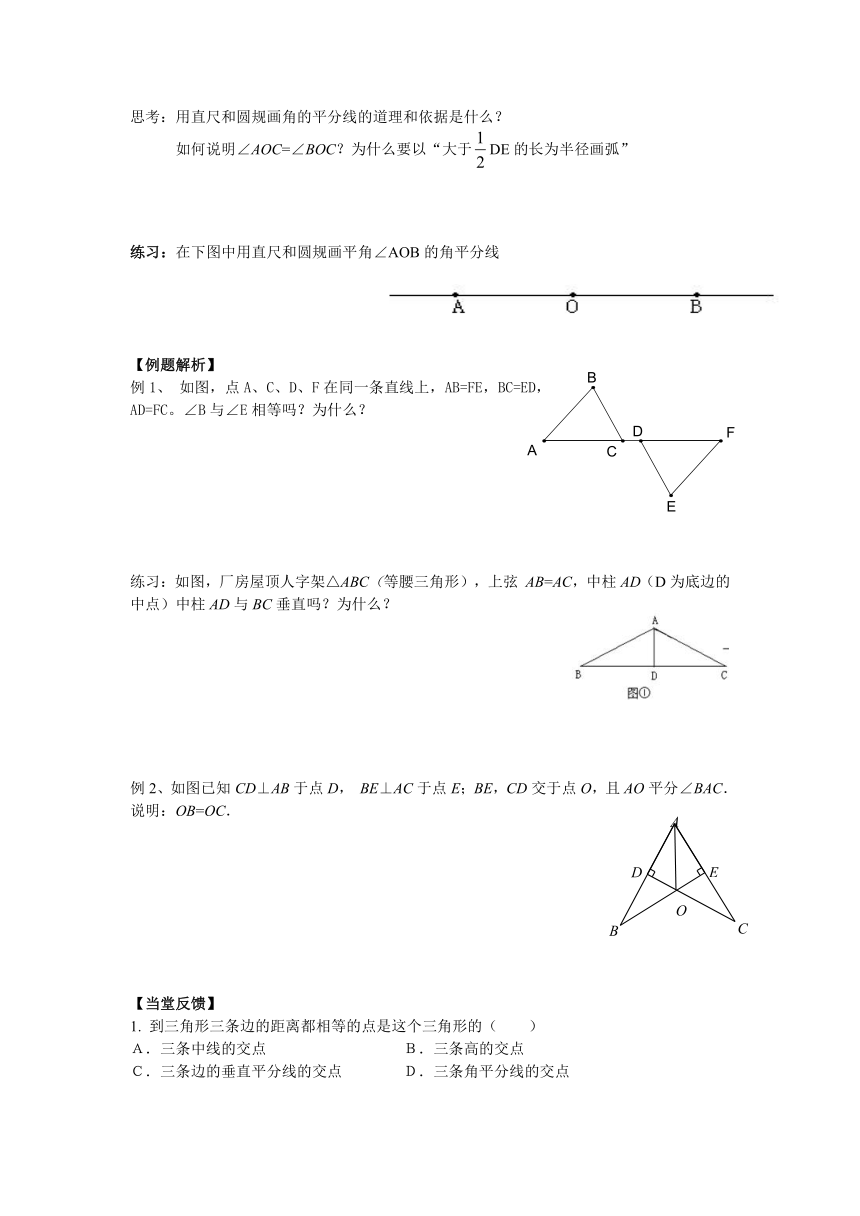
思考:用直尺和圆规画角的平分线的道理和依据是什么?
如何说明∠AOC=∠BOC?为什么要以“大于DE的长为半径画弧”
练习:在下图中用直尺和圆规画平角∠AOB的角平分线
【例题解析】
例1、 如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,
AD=FC。∠B与∠E相等吗?为什么?
练习:如图,厂房屋顶人字架△ABC(等腰三角形),上弦 AB=AC,中柱AD(D为底边的中点)中柱AD与BC垂直吗?为什么?
例2、如图已知CD⊥AB于点D, BE⊥AC于点E;BE,CD交于点O,且AO平分∠BAC.
说明:OB=OC.
【当堂反馈】
1. 到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
2. 如图,的角平分线AD交BC于 点D,,则点D到AB的距离是( )A.1 B.2 C.3 D.4
(2题) (3题) (4题)
3. 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=3,则点P到AB的距离是( )
A.3 B.4 C.5 D.6
4. 如图,OP平分,,,垂足分别为A,B.下列结论中不一定成立的是( )
A. B.平分
C. D.垂直平分
5.如图,已知△ABC中,AB=AC,D是BC的中点,求证:D到AB、AC的距离相等.
【课后作业】
1. 如图, 点 P到∠AOB两边的距离相等,若∠POB=30°,
则 ∠AOB=_____度.
2.在△ABC和△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.试说明:CE=BD.
3.架设电线杆时,小明想,如果我们先剪4根无弹性的绳索,将长度不等的两根绳索的一端分别重合打结C,D,然后将长度相等的两根绳索的另一端也分别重合打结,将结点C、D放在架设点两侧的地面上,并使它们距架设点的距离相等,三点C,O,D在同一直线上,最后将结点A、B分别系在电线杆上,调节电线杆的倾斜度和结点A、B的位置,使绳索充分拉紧.这样,从现在这个方向看电线杆便垂直于地面.你认为他说的有道理吗?
【拓展延伸】
1.已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,说明:点F在∠A的平分线上.
A
B
C
D
E
O
O
B
A
P
A
D
B
C
E
A
C
B
O
D
班级___________ 姓名___________学号___________
【学习目标】
⒈让学生进一步了解全等三角形在生活和生产中的应用,增强应用数学的意识;
⒉会用直尺和圆规作角平分线,并能有条理地说理和表达;
3.使学生掌握角平分线的性质和识别的方法,并会用解决有关简单问题.
【课前准备】
1、三角形全等的判定有哪几个?
2、如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,
③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有 ( )个. A.4 B.3 C.2 D.1
3.角平分线的定义: .
4.角平分线的性质: .
【探索新知】
小时候,我们都折过纸飞机,它的翼面如右图形状,你能说出它的特征吗?这样做有什么好处?
活动1.不利用任何工具,请你将一张用纸片做的角分成两个相等的角.你有什么方法?
活动2.如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
数学来源于生活,古代的能工巧匠就找到了解决的办法
如右图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB 、A沿着角的两边放下,沿AC画一条射线AE,则AE就是角平分线,你能说出其中的道理吗?
2. 工人师傅常常用角尺平分一个任意角,在∠COD的两边OC、OD上分别取OA=OB,移动角尺,使角的两边相同刻度分别与点A、B重合,这时过角尺顶点M的射线OM就是∠COD的平分线,请你说明这样画角平分线的道理.
【探究新知】
那么根据角平分仪的制作原理怎样作一个角的平分线?
画法 图形
1.以O为圆心,任意长为半径画弧,分别交射线OA、OB于点D、E2.分别以D、E为圆心,大于 DE的长度画弧,两弧在∠AOB的内部交于点C.3.画射线OC,OC就是∠AOB的角平分线
思考:用直尺和圆规画角的平分线的道理和依据是什么?
如何说明∠AOC=∠BOC?为什么要以“大于DE的长为半径画弧”
练习:在下图中用直尺和圆规画平角∠AOB的角平分线
【例题解析】
例1、 如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,
AD=FC。∠B与∠E相等吗?为什么?
练习:如图,厂房屋顶人字架△ABC(等腰三角形),上弦 AB=AC,中柱AD(D为底边的中点)中柱AD与BC垂直吗?为什么?
例2、如图已知CD⊥AB于点D, BE⊥AC于点E;BE,CD交于点O,且AO平分∠BAC.
说明:OB=OC.
【当堂反馈】
1. 到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
2. 如图,的角平分线AD交BC于 点D,,则点D到AB的距离是( )A.1 B.2 C.3 D.4
(2题) (3题) (4题)
3. 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=3,则点P到AB的距离是( )
A.3 B.4 C.5 D.6
4. 如图,OP平分,,,垂足分别为A,B.下列结论中不一定成立的是( )
A. B.平分
C. D.垂直平分
5.如图,已知△ABC中,AB=AC,D是BC的中点,求证:D到AB、AC的距离相等.
【课后作业】
1. 如图, 点 P到∠AOB两边的距离相等,若∠POB=30°,
则 ∠AOB=_____度.
2.在△ABC和△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.试说明:CE=BD.
3.架设电线杆时,小明想,如果我们先剪4根无弹性的绳索,将长度不等的两根绳索的一端分别重合打结C,D,然后将长度相等的两根绳索的另一端也分别重合打结,将结点C、D放在架设点两侧的地面上,并使它们距架设点的距离相等,三点C,O,D在同一直线上,最后将结点A、B分别系在电线杆上,调节电线杆的倾斜度和结点A、B的位置,使绳索充分拉紧.这样,从现在这个方向看电线杆便垂直于地面.你认为他说的有道理吗?
【拓展延伸】
1.已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,说明:点F在∠A的平分线上.
A
B
C
D
E
O
O
B
A
P
A
D
B
C
E
A
C
B
O
D
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
