湘教版 七下 4.3平行线的性质同步课时训练试卷(word版含答案)
文档属性
| 名称 | 湘教版 七下 4.3平行线的性质同步课时训练试卷(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 370.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 15:18:49 | ||
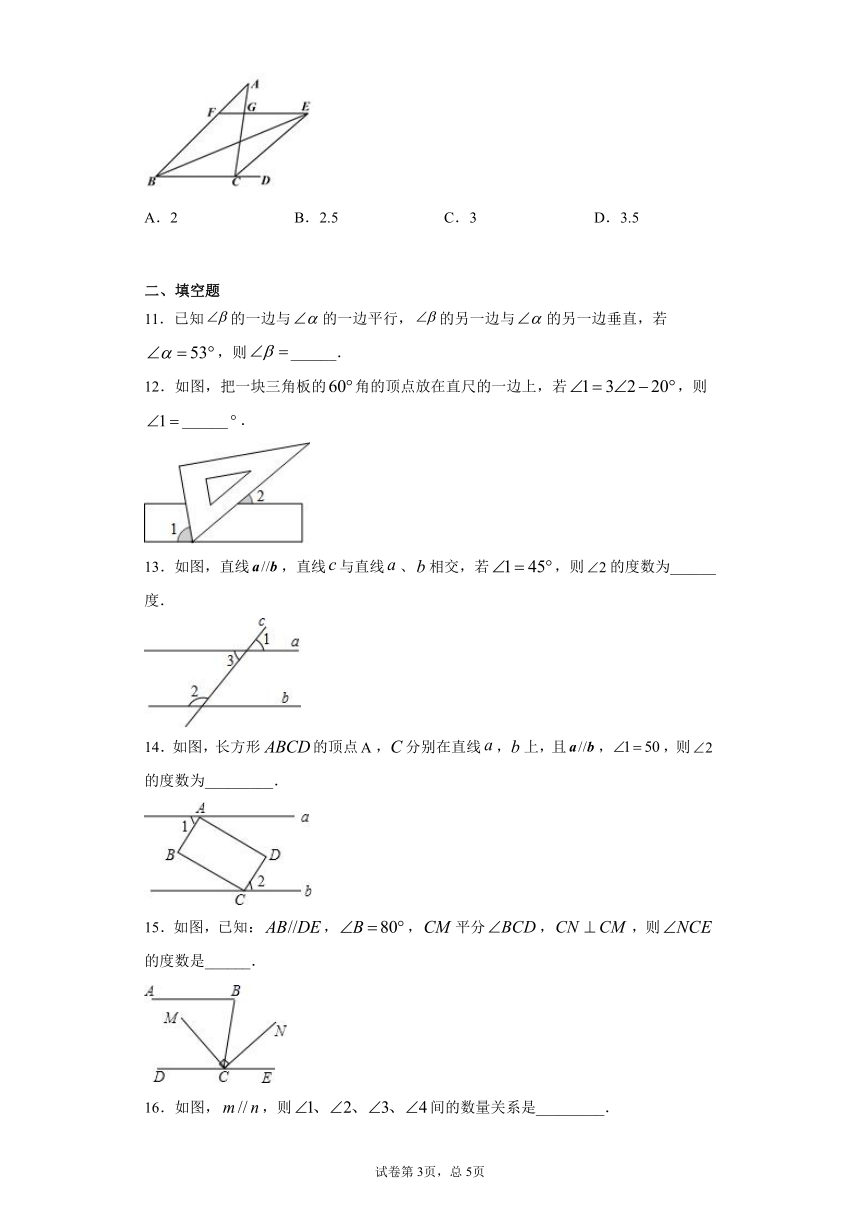
图片预览



文档简介
4.3平行线的性质同步课时训练
一、单选题
1.如图,平行线,被直线所截.若,则的度数为( )
A. B. C. D.
2.如图,将直尺与含30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )
A.40° B.60° C.70° D.80°
3.如图,,那么图中与∠AFE相等的角的个数是( )
A.4 B.5 C.6 D.7
4.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35° B.45° C.50° D.55°
5.如图,直线,,则的度数为( ).
A. B. C. D.
6.如图,直线与直线相交,将直线沿的方向平移得到直线,若,则的度数为( )
A.105° B.115° C.120° D.125°
7.如图,平分,,若,则的度数为( )
A. B. C. D.
8.已知的两边与的两边分别平行,若的度数比的2倍少30°,则的度数是( )
A.30° B.50° C.30°或70° D.50°或70°
9.一把直尺与30°的直角三角板如图所示,,则( )
A.50° B.60° C.70° D.80°
10.如图,BE,CE分别平分∠ABC,∠ACD,EF∥BC,交AB于点F,交AC于点G,若BF=7,CG=5,则FG长为( )
A.2 B.2.5 C.3 D.3.5
二、填空题
11.已知的一边与的一边平行,的另一边与的另一边垂直,若,则______.
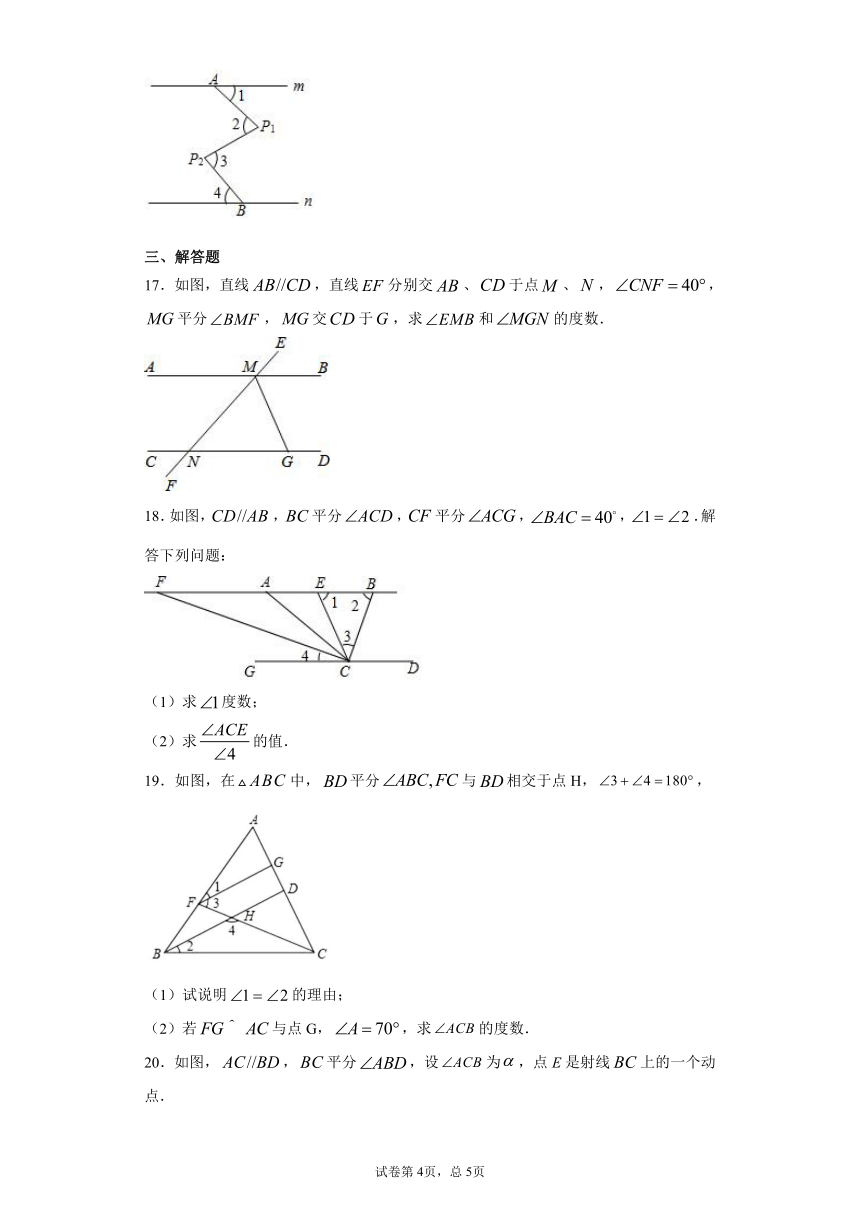
12.如图,把一块三角板的角的顶点放在直尺的一边上,若,则______.
13.如图,直线,直线与直线、相交,若,则的度数为______度.
14.如图,长方形的顶点,分别在直线,上,且,,则的度数为_________.
15.如图,已知:,,平分,,则的度数是______.
16.如图,,则间的数量关系是_________.
三、解答题
17.如图,直线,直线分别交、于点、,,平分,交于,求和的度数.
18.如图,,平分,平分,,.解答下列问题:
(1)求度数;
(2)求的值.
19.如图,在中,平分与相交于点H,,
(1)试说明的理由;
(2)若与点G,,求的度数.
20.如图,,平分,设为,点E是射线上的一个动点.
(1)若时,且,求的度数;
(2)若点E运动到上方,且满足,,求的值;
(3)若,求的度数(用含n和的代数式表示).
参考答案
1.A
2.D
3.B
4.A
5.C
6.B
7.C
8.C
9.C
10.A
11.143°或37°
12.85
13.135°
14.50°
15.40°
16.∠2+∠4=∠1+∠3
17.∠EMB=40°,∠MGN=70°
【详解】
解:∵AB∥CD,
∴∠AMN=∠CNF=40°,
∴∠EMB=∠AMN=40°,
∴∠BMN=140°,
又∵MG平分∠BMF,
∴∠BMG=∠BMN=70°,
∵AB∥CD,
∴∠MGN=∠BMG=70°.
18.(1)70°;(2)
【详解】
解:(1)∵BC平分∠ACD,CF平分∠ACG,
∴∠ACB=∠ACD,∠ACF=∠ACG,
∵∠ACG+∠ACD=180°,
∴∠ACF+∠ACB=90°,
∴CB⊥CF,
∵∠BAC=40°,∵CD//AB,
∴∠ACG=40°,
∴∠ACF=20°,
∴∠ACB=90°-20°=70°,
∴∠BCD=70°,
∵CD∥AB,
∴∠2=∠BCD=70°,
∵∠1=∠2,
∴∠1=70°;
(2)∵∠BCD=70°,
∴∠ACB=70°,
∵∠1=∠2=70°,
∴∠3=40°,
∴∠ACE=30°,
∵CF平分∠ACG,
∴∠ACF=∠4=20°,
∴==.
19.(1)见解析;(2)70°
【详解】
解:(1)∵∠3+∠4=180°,∠FHD=∠4,
∴∠3+∠FHD=180°,
∴FG∥BD,
∴∠1=∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠2,
∴∠1=∠2;
(2)∵FG⊥AC,∠A=70°,
∴∠1=90°-70°=20°,
∴∠2=∠ABD=∠1=20°,
∴∠ABC=∠2+∠ABD=40°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ACB=180°-∠A-∠ABC=180°-70°-40°=70°.
20.(1)60°;(2)50°;(3)或
【详解】
解:(1),,
,
平分,
,
,
又,
;
(2)根据题意画图,如图1所示,
,,
,
,
,
,
又平分,
,
;
(3)①如图2所示,
,
,
平分,
,
,
又,
,
,
解得;
②如图3所示,
,
,
平分,
,
,
又,
,
,
解得.
综上的度数为或.
一、单选题
1.如图,平行线,被直线所截.若,则的度数为( )
A. B. C. D.
2.如图,将直尺与含30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )
A.40° B.60° C.70° D.80°
3.如图,,那么图中与∠AFE相等的角的个数是( )
A.4 B.5 C.6 D.7
4.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35° B.45° C.50° D.55°
5.如图,直线,,则的度数为( ).
A. B. C. D.
6.如图,直线与直线相交,将直线沿的方向平移得到直线,若,则的度数为( )
A.105° B.115° C.120° D.125°
7.如图,平分,,若,则的度数为( )
A. B. C. D.
8.已知的两边与的两边分别平行,若的度数比的2倍少30°,则的度数是( )
A.30° B.50° C.30°或70° D.50°或70°
9.一把直尺与30°的直角三角板如图所示,,则( )
A.50° B.60° C.70° D.80°
10.如图,BE,CE分别平分∠ABC,∠ACD,EF∥BC,交AB于点F,交AC于点G,若BF=7,CG=5,则FG长为( )
A.2 B.2.5 C.3 D.3.5
二、填空题
11.已知的一边与的一边平行,的另一边与的另一边垂直,若,则______.
12.如图,把一块三角板的角的顶点放在直尺的一边上,若,则______.
13.如图,直线,直线与直线、相交,若,则的度数为______度.
14.如图,长方形的顶点,分别在直线,上,且,,则的度数为_________.
15.如图,已知:,,平分,,则的度数是______.
16.如图,,则间的数量关系是_________.
三、解答题
17.如图,直线,直线分别交、于点、,,平分,交于,求和的度数.
18.如图,,平分,平分,,.解答下列问题:
(1)求度数;
(2)求的值.
19.如图,在中,平分与相交于点H,,
(1)试说明的理由;
(2)若与点G,,求的度数.
20.如图,,平分,设为,点E是射线上的一个动点.
(1)若时,且,求的度数;
(2)若点E运动到上方,且满足,,求的值;
(3)若,求的度数(用含n和的代数式表示).
参考答案
1.A
2.D
3.B
4.A
5.C
6.B
7.C
8.C
9.C
10.A
11.143°或37°
12.85
13.135°
14.50°
15.40°
16.∠2+∠4=∠1+∠3
17.∠EMB=40°,∠MGN=70°
【详解】
解:∵AB∥CD,
∴∠AMN=∠CNF=40°,
∴∠EMB=∠AMN=40°,
∴∠BMN=140°,
又∵MG平分∠BMF,
∴∠BMG=∠BMN=70°,
∵AB∥CD,
∴∠MGN=∠BMG=70°.
18.(1)70°;(2)
【详解】
解:(1)∵BC平分∠ACD,CF平分∠ACG,
∴∠ACB=∠ACD,∠ACF=∠ACG,
∵∠ACG+∠ACD=180°,
∴∠ACF+∠ACB=90°,
∴CB⊥CF,
∵∠BAC=40°,∵CD//AB,
∴∠ACG=40°,
∴∠ACF=20°,
∴∠ACB=90°-20°=70°,
∴∠BCD=70°,
∵CD∥AB,
∴∠2=∠BCD=70°,
∵∠1=∠2,
∴∠1=70°;
(2)∵∠BCD=70°,
∴∠ACB=70°,
∵∠1=∠2=70°,
∴∠3=40°,
∴∠ACE=30°,
∵CF平分∠ACG,
∴∠ACF=∠4=20°,
∴==.
19.(1)见解析;(2)70°
【详解】
解:(1)∵∠3+∠4=180°,∠FHD=∠4,
∴∠3+∠FHD=180°,
∴FG∥BD,
∴∠1=∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠2,
∴∠1=∠2;
(2)∵FG⊥AC,∠A=70°,
∴∠1=90°-70°=20°,
∴∠2=∠ABD=∠1=20°,
∴∠ABC=∠2+∠ABD=40°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ACB=180°-∠A-∠ABC=180°-70°-40°=70°.
20.(1)60°;(2)50°;(3)或
【详解】
解:(1),,
,
平分,
,
,
又,
;
(2)根据题意画图,如图1所示,
,,
,
,
,
,
又平分,
,
;
(3)①如图2所示,
,
,
平分,
,
,
又,
,
,
解得;
②如图3所示,
,
,
平分,
,
,
又,
,
,
解得.
综上的度数为或.
