苏科版七年级下11.3探索三角形全等的条件(3)教学案
文档属性
| 名称 | 苏科版七年级下11.3探索三角形全等的条件(3)教学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 55.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-02 00:00:00 | ||
图片预览

文档简介
11.3探索三角形全等的条件(3)
主备:吕云华 审核:
班级___________ 姓名___________学号__________
【学习目标】
1. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2. 记住全等三角形的识别方法(S.S.S),并会运用该方法判断三角形是否全等.
3. 了解三角形的稳定性.
【课前准备】
1.三角形全等的判定学过哪几个?
2.角平分线上的点到________________________________相等
3.如图,已知AC与BD相交于点O,AD//BC,AD=BC,△AOD≌△COB吗?为什么?
【探索新知】
情景1:小张用分别为5、6、7的3根木棒搭出了△ABC,试问:小美应选用怎样的3根木棒才能搭出△MNP与△ABC全等?
活动一: 用铁丝围全等三角形
课前准备长20cm的细铁丝或者铝丝,小组分别讨论,尝试探索,设计可行的方案,并制作三角形,展示各组成果.怎样才能使你和同学围成的三角形全等?
活动二:用直尺和圆规作三角形
每一位学生按下列步骤作图
画线段AB=4cm.
分别以点A点B为圆心,3cm,2cm的长为半径画弧,两弧相交于点C.
连接AC、BC
作图区域
归纳___________________两个三角形全等.简写为“边边边”或简记为(SSS.)
上面的结论告诉我们,如果一个三角形的三边确定,那么这个三角形的形状和大小就完全确定,三角形的这种性质叫做三角形的稳定性。
活动三:学生利用周末制作木制三角形和四边形,探究图形的稳定性
思考:三角形为什么具备稳定性?有什么办法让四边形也具备稳定性?
说说你周围应用三角形稳定性的实际例子,以感受数学的价值,增强应用数学的意识,学会用数学的眼光去观察、分析周围的事物。
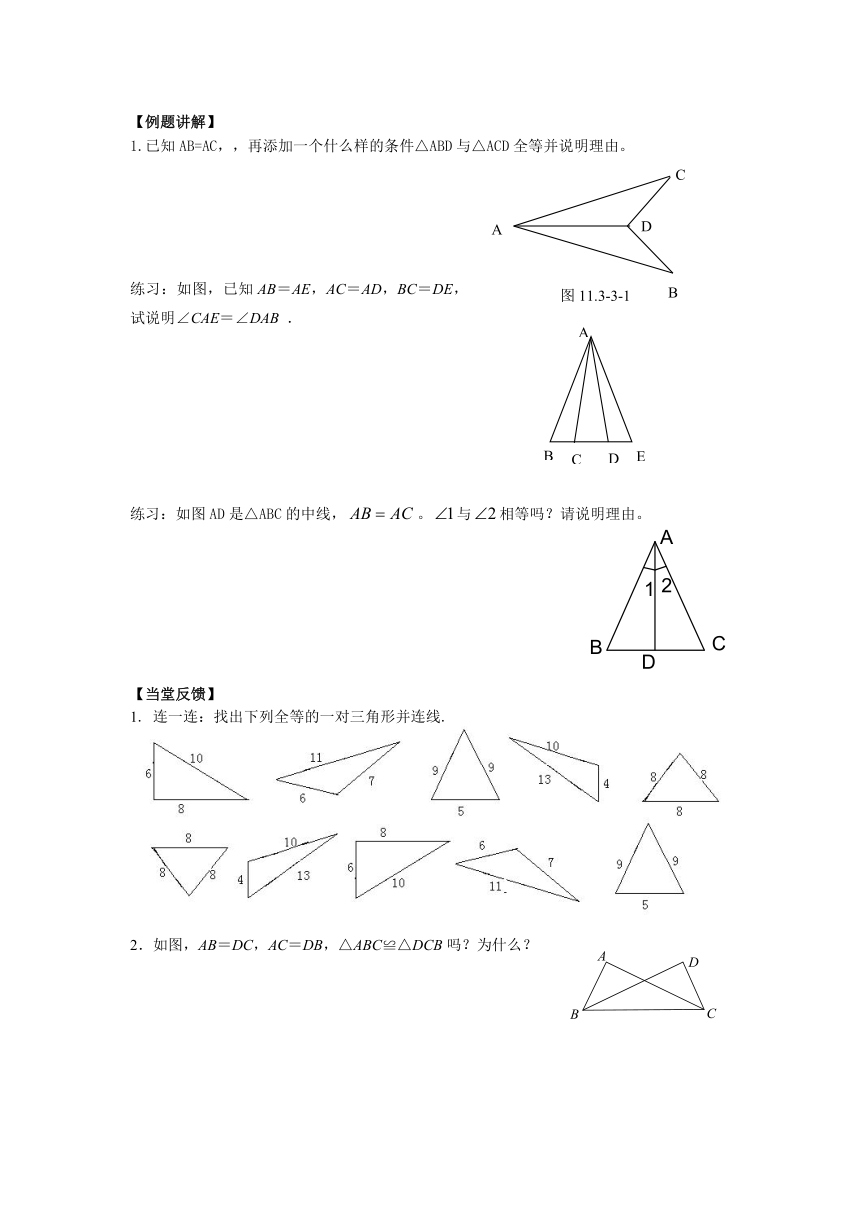
【例题讲解】
1.已知AB=AC,,再添加一个什么样的条件△ABD与△ACD全等并说明理由。
练习:如图,已知AB=AE,AC=AD,BC=DE,试说明∠CAE=∠DAB .
练习:如图AD是△ABC的中线,。与相等吗?请说明理由。
【当堂反馈】
1. 连一连:找出下列全等的一对三角形并连线.
2.如图,AB=DC,AC=DB,△ABC≌△DCB吗?为什么?
3、如图5-5-4,AB=DF,AC=DE,BE=CF。你能找到一对全等三角形吗?说明你的理由。
【课后作业】
1. 已知图中的两个三角形全等,则的度数是( )
A.72° B.60° C.58° D.50°
2.如图,在与中,已有条件,还需添加两个条件才能使,不能添加的一组条件是( )
A.,
B.,
C., D.,
3. 如图,给出下列四组条件:
①;
②;
③;
④.
其中,能使的条件共有( )
A.1组 B.2组 C.3组 D.4组
4. 如图,若,且,则= .
5如图,在ΔABC与ΔAED中,AB=AE,AC=AD,请补充一个已知条件:____________(写一个即可),使ΔABC≌ΔAED. 试说明理由.
【拓展延伸】
1..你还记得怎样用尺规作一个角等于已知角吗?你能说明其中的道理吗?
2.已知如图,AB=CD,CE=DF,AE=BF,则AE∥DF吗 为什么
3.如图,已知AB=AC,BD=CD,试用“边边边”识别法说明:∠B=∠Cw ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
4.如图方格纸中的3个顶点分别在小正方形的顶点(格点)上,这样的三角形角格点三角形。请你在图中画一个格点△ABC,且使△ABC≌,这样的格点三角形你能花几个?
A
D
O
C
B
A
B
C
D
图11.3-3-1
C
B
A
E
D
a
c
c
a
b
50°
58°
72°
A
B
C
D
E
F
A
C
B
D
F
E
图3
A
B
C
C1
A1
B1
图8
主备:吕云华 审核:
班级___________ 姓名___________学号__________
【学习目标】
1. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2. 记住全等三角形的识别方法(S.S.S),并会运用该方法判断三角形是否全等.
3. 了解三角形的稳定性.
【课前准备】
1.三角形全等的判定学过哪几个?
2.角平分线上的点到________________________________相等
3.如图,已知AC与BD相交于点O,AD//BC,AD=BC,△AOD≌△COB吗?为什么?
【探索新知】
情景1:小张用分别为5、6、7的3根木棒搭出了△ABC,试问:小美应选用怎样的3根木棒才能搭出△MNP与△ABC全等?
活动一: 用铁丝围全等三角形
课前准备长20cm的细铁丝或者铝丝,小组分别讨论,尝试探索,设计可行的方案,并制作三角形,展示各组成果.怎样才能使你和同学围成的三角形全等?
活动二:用直尺和圆规作三角形
每一位学生按下列步骤作图
画线段AB=4cm.
分别以点A点B为圆心,3cm,2cm的长为半径画弧,两弧相交于点C.
连接AC、BC
作图区域
归纳___________________两个三角形全等.简写为“边边边”或简记为(SSS.)
上面的结论告诉我们,如果一个三角形的三边确定,那么这个三角形的形状和大小就完全确定,三角形的这种性质叫做三角形的稳定性。
活动三:学生利用周末制作木制三角形和四边形,探究图形的稳定性
思考:三角形为什么具备稳定性?有什么办法让四边形也具备稳定性?
说说你周围应用三角形稳定性的实际例子,以感受数学的价值,增强应用数学的意识,学会用数学的眼光去观察、分析周围的事物。
【例题讲解】
1.已知AB=AC,,再添加一个什么样的条件△ABD与△ACD全等并说明理由。
练习:如图,已知AB=AE,AC=AD,BC=DE,试说明∠CAE=∠DAB .
练习:如图AD是△ABC的中线,。与相等吗?请说明理由。
【当堂反馈】
1. 连一连:找出下列全等的一对三角形并连线.
2.如图,AB=DC,AC=DB,△ABC≌△DCB吗?为什么?
3、如图5-5-4,AB=DF,AC=DE,BE=CF。你能找到一对全等三角形吗?说明你的理由。
【课后作业】
1. 已知图中的两个三角形全等,则的度数是( )
A.72° B.60° C.58° D.50°
2.如图,在与中,已有条件,还需添加两个条件才能使,不能添加的一组条件是( )
A.,
B.,
C., D.,
3. 如图,给出下列四组条件:
①;
②;
③;
④.
其中,能使的条件共有( )
A.1组 B.2组 C.3组 D.4组
4. 如图,若,且,则= .
5如图,在ΔABC与ΔAED中,AB=AE,AC=AD,请补充一个已知条件:____________(写一个即可),使ΔABC≌ΔAED. 试说明理由.
【拓展延伸】
1..你还记得怎样用尺规作一个角等于已知角吗?你能说明其中的道理吗?
2.已知如图,AB=CD,CE=DF,AE=BF,则AE∥DF吗 为什么
3.如图,已知AB=AC,BD=CD,试用“边边边”识别法说明:∠B=∠Cw ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
4.如图方格纸中的3个顶点分别在小正方形的顶点(格点)上,这样的三角形角格点三角形。请你在图中画一个格点△ABC,且使△ABC≌,这样的格点三角形你能花几个?
A
D
O
C
B
A
B
C
D
图11.3-3-1
C
B
A
E
D
a
c
c
a
b
50°
58°
72°
A
B
C
D
E
F
A
C
B
D
F
E
图3
A
B
C
C1
A1
B1
图8
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
