湘教版 八下 1.2直角三角形的性质与判定(二)同步课时训练试卷(word版含答案)
文档属性
| 名称 | 湘教版 八下 1.2直角三角形的性质与判定(二)同步课时训练试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 427.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览


文档简介
1.2直角三角形的性质与判定(二)同步课时训练
一、单选题(共40分)
1.(本题4分)已知三角形的三边长a、b、c满足+ +|c-|=0,则三角形的形状是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.不能确定
2.(本题4分)在中,已知,AD是的角平分线,于点E.若 的面积为S,则的面积为( )
A. B. C. D.
3.(本题4分)已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件中不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠C=∠A﹣∠B
C.a2﹣b2=c2 D.a:b:c=7:24:25
4.(本题4分)已知点P是内一点,且它到三角形的三个顶点距离之和最小,则P点叫的费马点(Fermat point).已经证明:在三个内角均小于的中,当时,P就是的费马点.若点P是腰长为的等腰直角三角形的费马点,则( )
A.6 B. C. D.9
5.(本题4分)如图,已知图中所有的四边形都是正方形,所有的三角形都是直角三角形.若其中每个直角三角形的最长边与最短边的长度之比均为k,正方形A,B,C,D的面积分别为S1,S2,S3,S4,且S1>S2,S3>S4,则下列结论正确的是( )
A.S1?S4=k2S2 B.S1+S4=S22 C.S1?S4=S22 D.S1+S4=kS2
6.(本题4分)在一个直角三角形中,如果一条直角边长是3,另一条直角边长是4,那么斜边长是( )
A.5 B. C.5或 D.不确定
7.(本题4分)如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为(?? )
A.2a B.2 a C.3a D.
8.(本题4分)如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可以表示为( )
A.S1﹣S2 B.S1+S2 C.2S1﹣S2 D.S1+2S2
9.(本题4分)在平面直角坐标系中,A(0,3),B(4,0),把△AOB绕点O旋转,使点A,B分别落在点A′,B′处,若A′B′∥x轴,点B′在第一象限,则点A的对应点A′的坐标为( )
A.() B.() C.() D.()
10.(本题4分)如图,平面直角坐标系中,O是坐标原点,点A(3,2),点P(m,0),若△POA是等腰三角形,则m可取的值最多有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(共24分)
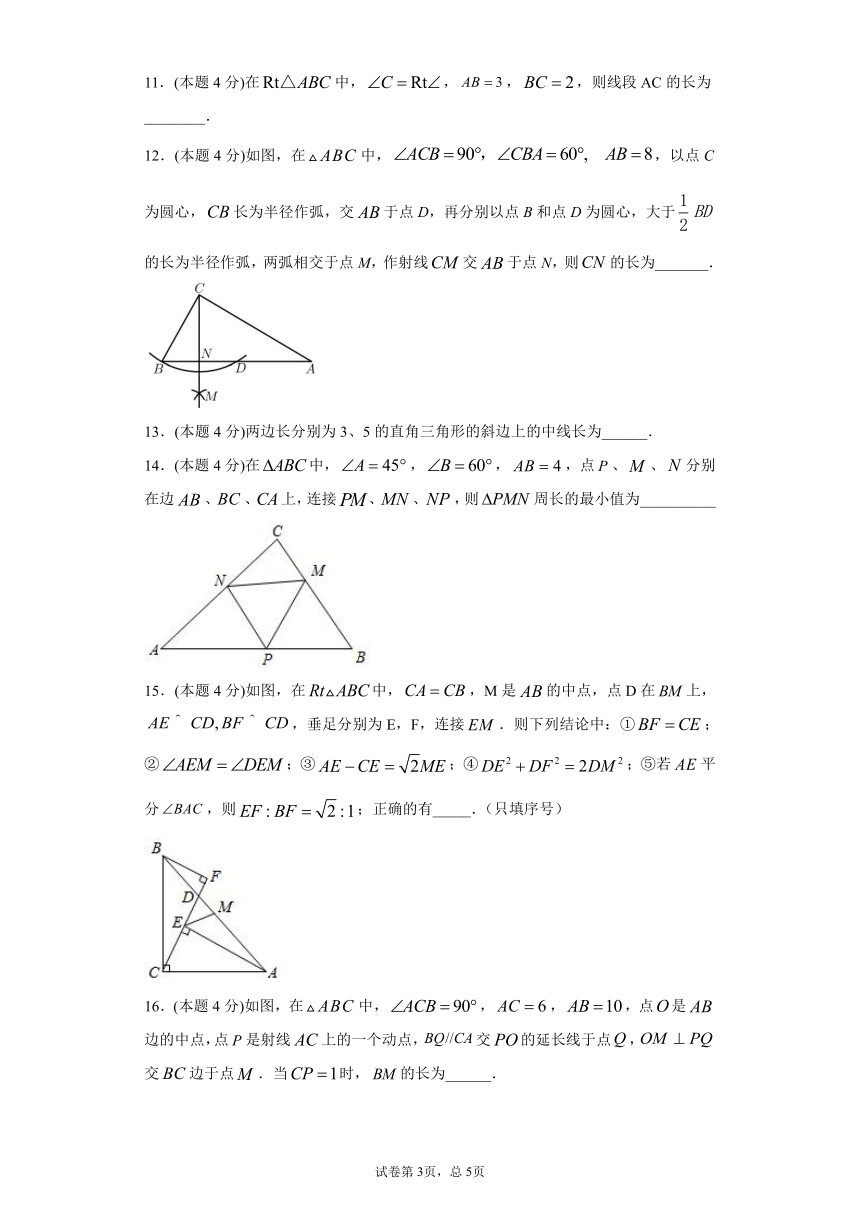
11.(本题4分)在中,,,,则线段AC的长为________.
12.(本题4分)如图,在中,,以点C为圆心,长为半径作弧,交于点D,再分别以点B和点D为圆心,大于的长为半径作弧,两弧相交于点M,作射线交于点N,则的长为_______.
13.(本题4分)两边长分别为3、5的直角三角形的斜边上的中线长为______.
14.(本题4分)在中,,,,点、、分别在边、、上,连接、、,则周长的最小值为__________
15.(本题4分)如图,在中,,M是的中点,点D在上,,垂足分别为E,F,连接.则下列结论中:①;②;③;④;⑤若平分,则;正确的有_____.(只填序号)
16.(本题4分)如图,在中,,,,点是边的中点,点是射线上的一个动点,交的延长线于点,交边于点.当时,的长为______.
三、解答题(共36分)
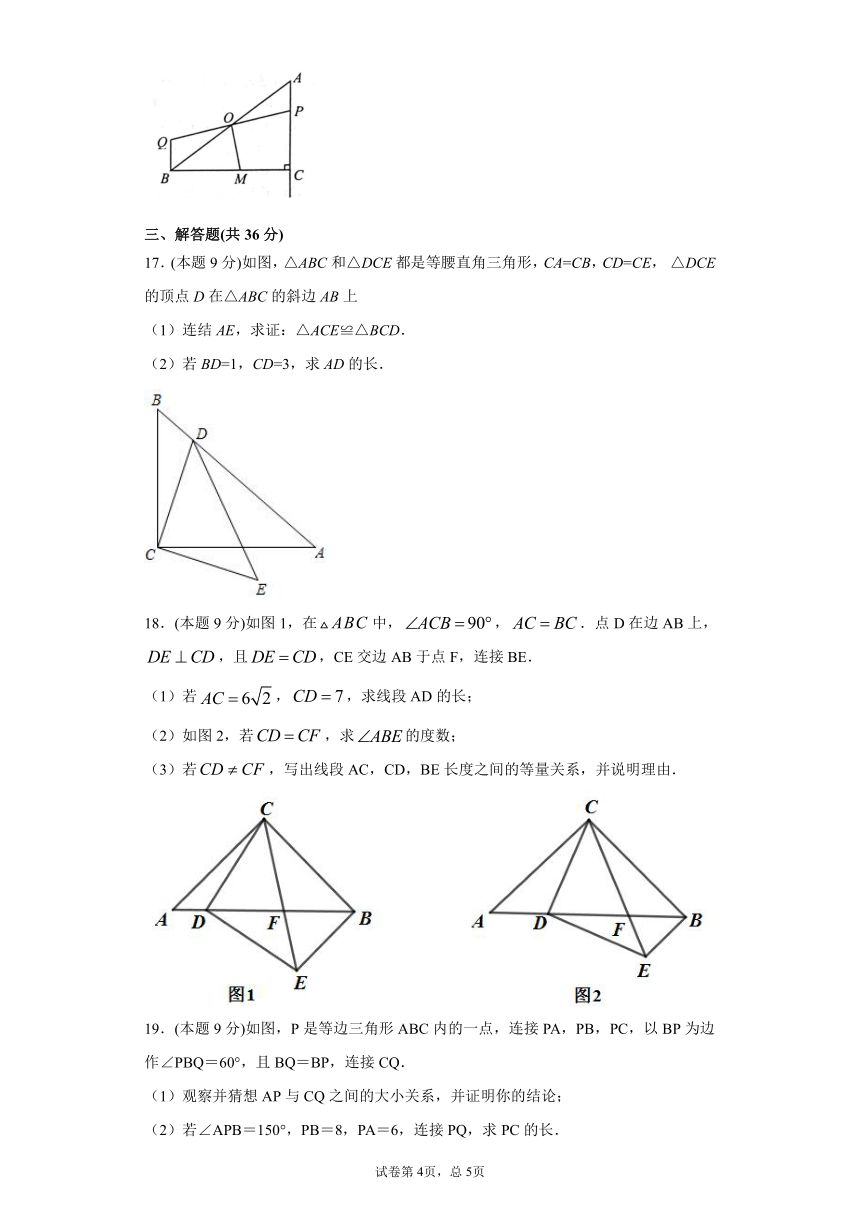
17.(本题9分)如图,△ABC和△DCE都是等腰直角三角形,CA=CB,CD=CE, △DCE的顶点D在△ABC的斜边AB上
(1)连结AE,求证:△ACE≌△BCD.
(2)若BD=1,CD=3,求AD的长.
18.(本题9分)如图1,在中,,.点D在边AB上,,且,CE交边AB于点F,连接BE.
(1)若,,求线段AD的长;
(2)如图2,若,求的度数;
(3)若,写出线段AC,CD,BE长度之间的等量关系,并说明理由.
19.(本题9分)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2)若∠APB=150°,PB=8,PA=6,连接PQ,求PC的长.
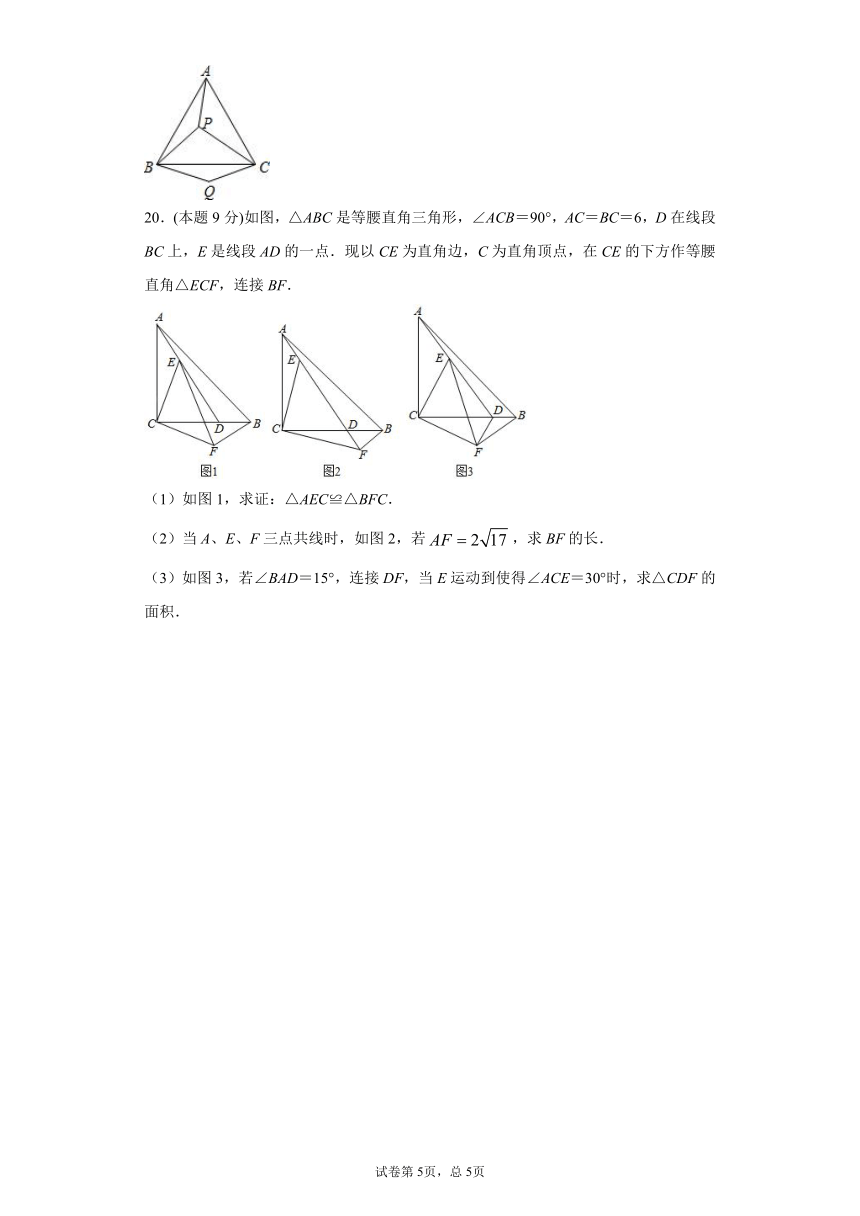
20.(本题9分)如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=6,D在线段BC上,E是线段AD的一点.现以CE为直角边,C为直角顶点,在CE的下方作等腰直角△ECF,连接BF.
(1)如图1,求证:△AEC≌△BFC.
(2)当A、E、F三点共线时,如图2,若,求BF的长.
(3)如图3,若∠BAD=15°,连接DF,当E运动到使得∠ACE=30°时,求△CDF的面积.
参考答案
1.C
2.B
3.A
4.B
5.C
6.A
7.B
8.C
9.A
10.C
11.
12.
13.或
14.2
15.①②③④⑤
16.2.5或1
17.(1)见解析;(2)
【详解】
(1)△ABC和△DCE都是等腰直角三角形
,,
,
△ACE≌△BCD(SAS);
(2)△ACE≌△BCD
为直角三角形
为等腰直角三角形
△ACE≌△BCD
BD=AE=1
18.(1);(2)∠ABE=45°;(3),证明见解析.
【详解】
解:(1)如下图,过点C作CM⊥AB,
∵,,
∴,
∵CM⊥AB,
∴,
∵,
∴,
∴;
(2)如下图,过点C作CM⊥AB于点M,EN⊥AB于点N,
∴∠CMD=∠DNE=90°,
∴∠MCD+∠MDC=90°,
又∵,
∴∠MDC+∠NDE=90°,
∴∠MCD=∠NDE,
在△CDM和△DEN中,
,
∴△CDM≌△DEN(AAS)
,
∴,
∴,
∴△BNE为等腰直角三角形,
∴∠ABE=45°,
(3)由(2)可知,,
∴,
又∵,
∴,
在Rt△ACM中,,
∴,
在Rt△CDM中,,
∴,
∴,
故线段AC,CD,BE长度之间等量关系为:.
19.(1)AP=CQ,证明见解析;(2)10.
【详解】
解:(1)AP=CQ.
证明:∵△ABC为等边三角形,
∴∠ABC=60°,AB=CB,
∴∠ABP+∠PBC=60°.
又∵∠PBQ=∠PBC+∠CBQ=60°,
∴∠ABP=∠CBQ.
在△ABP和△CBQ中,
,
∴△ABP≌△CBQ(SAS),
∴AP=CQ.
(2)连接PQ,如图所示.
∵△ABP≌△CBQ,
∴∠BQC=∠BPA=150°.
∵BP=BQ,∠PBQ=60°,
∴△PBQ为等边三角形,
∴PQ=PB=8,∠BQP=60°,
∴∠PQC=90°.
在Rt△PQC中,∠PQC=90°,PQ=8,CQ=AP=6,
∴PC==10.
20.(1)证明见解析;(2);(3)
【详解】
(1)证明: ∵△ACB,△ECF都是等腰三角形,
∴CA=CB,CE=CF,∠ACB=∠ECF=90°,
∴∠ACE=∠BCF,
∴△AEC≌△BFC(SAS),
(2)解:∵CA=CB=6,∠ACB=90°,
∴,
∵△ACE≌△BCF,
∴∠CAD=∠DBF,
∵∠ADC=∠BDF,
∴∠ACD=∠DFB=90°,
∴
(3)如图,作FH⊥BC于H.
∠ACE=∠CAE=30°,
∴AE=EC,
∵△ACE≌△BCF,
∴BF=AE,CF=CE,
∴CF=BF,∠FCB=∠CBF=30°,
∵FC=FB,FH⊥BC,
∴CH=BH=3,
由
(负根舍去),,
∵∠CED=∠CAE+∠ACE=60°,∠ECD=90°﹣30°=60°,
∴△ECD是等边三角形,
∴,
∴.
一、单选题(共40分)
1.(本题4分)已知三角形的三边长a、b、c满足+ +|c-|=0,则三角形的形状是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.不能确定
2.(本题4分)在中,已知,AD是的角平分线,于点E.若 的面积为S,则的面积为( )
A. B. C. D.
3.(本题4分)已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件中不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠C=∠A﹣∠B
C.a2﹣b2=c2 D.a:b:c=7:24:25
4.(本题4分)已知点P是内一点,且它到三角形的三个顶点距离之和最小,则P点叫的费马点(Fermat point).已经证明:在三个内角均小于的中,当时,P就是的费马点.若点P是腰长为的等腰直角三角形的费马点,则( )
A.6 B. C. D.9
5.(本题4分)如图,已知图中所有的四边形都是正方形,所有的三角形都是直角三角形.若其中每个直角三角形的最长边与最短边的长度之比均为k,正方形A,B,C,D的面积分别为S1,S2,S3,S4,且S1>S2,S3>S4,则下列结论正确的是( )
A.S1?S4=k2S2 B.S1+S4=S22 C.S1?S4=S22 D.S1+S4=kS2
6.(本题4分)在一个直角三角形中,如果一条直角边长是3,另一条直角边长是4,那么斜边长是( )
A.5 B. C.5或 D.不确定
7.(本题4分)如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为(?? )
A.2a B.2 a C.3a D.
8.(本题4分)如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可以表示为( )
A.S1﹣S2 B.S1+S2 C.2S1﹣S2 D.S1+2S2
9.(本题4分)在平面直角坐标系中,A(0,3),B(4,0),把△AOB绕点O旋转,使点A,B分别落在点A′,B′处,若A′B′∥x轴,点B′在第一象限,则点A的对应点A′的坐标为( )
A.() B.() C.() D.()
10.(本题4分)如图,平面直角坐标系中,O是坐标原点,点A(3,2),点P(m,0),若△POA是等腰三角形,则m可取的值最多有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(共24分)
11.(本题4分)在中,,,,则线段AC的长为________.
12.(本题4分)如图,在中,,以点C为圆心,长为半径作弧,交于点D,再分别以点B和点D为圆心,大于的长为半径作弧,两弧相交于点M,作射线交于点N,则的长为_______.
13.(本题4分)两边长分别为3、5的直角三角形的斜边上的中线长为______.
14.(本题4分)在中,,,,点、、分别在边、、上,连接、、,则周长的最小值为__________
15.(本题4分)如图,在中,,M是的中点,点D在上,,垂足分别为E,F,连接.则下列结论中:①;②;③;④;⑤若平分,则;正确的有_____.(只填序号)
16.(本题4分)如图,在中,,,,点是边的中点,点是射线上的一个动点,交的延长线于点,交边于点.当时,的长为______.
三、解答题(共36分)
17.(本题9分)如图,△ABC和△DCE都是等腰直角三角形,CA=CB,CD=CE, △DCE的顶点D在△ABC的斜边AB上
(1)连结AE,求证:△ACE≌△BCD.
(2)若BD=1,CD=3,求AD的长.
18.(本题9分)如图1,在中,,.点D在边AB上,,且,CE交边AB于点F,连接BE.
(1)若,,求线段AD的长;
(2)如图2,若,求的度数;
(3)若,写出线段AC,CD,BE长度之间的等量关系,并说明理由.
19.(本题9分)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2)若∠APB=150°,PB=8,PA=6,连接PQ,求PC的长.
20.(本题9分)如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=6,D在线段BC上,E是线段AD的一点.现以CE为直角边,C为直角顶点,在CE的下方作等腰直角△ECF,连接BF.
(1)如图1,求证:△AEC≌△BFC.
(2)当A、E、F三点共线时,如图2,若,求BF的长.
(3)如图3,若∠BAD=15°,连接DF,当E运动到使得∠ACE=30°时,求△CDF的面积.
参考答案
1.C
2.B
3.A
4.B
5.C
6.A
7.B
8.C
9.A
10.C
11.
12.
13.或
14.2
15.①②③④⑤
16.2.5或1
17.(1)见解析;(2)
【详解】
(1)△ABC和△DCE都是等腰直角三角形
,,
,
△ACE≌△BCD(SAS);
(2)△ACE≌△BCD
为直角三角形
为等腰直角三角形
△ACE≌△BCD
BD=AE=1
18.(1);(2)∠ABE=45°;(3),证明见解析.
【详解】
解:(1)如下图,过点C作CM⊥AB,
∵,,
∴,
∵CM⊥AB,
∴,
∵,
∴,
∴;
(2)如下图,过点C作CM⊥AB于点M,EN⊥AB于点N,
∴∠CMD=∠DNE=90°,
∴∠MCD+∠MDC=90°,
又∵,
∴∠MDC+∠NDE=90°,
∴∠MCD=∠NDE,
在△CDM和△DEN中,
,
∴△CDM≌△DEN(AAS)
,
∴,
∴,
∴△BNE为等腰直角三角形,
∴∠ABE=45°,
(3)由(2)可知,,
∴,
又∵,
∴,
在Rt△ACM中,,
∴,
在Rt△CDM中,,
∴,
∴,
故线段AC,CD,BE长度之间等量关系为:.
19.(1)AP=CQ,证明见解析;(2)10.
【详解】
解:(1)AP=CQ.
证明:∵△ABC为等边三角形,
∴∠ABC=60°,AB=CB,
∴∠ABP+∠PBC=60°.
又∵∠PBQ=∠PBC+∠CBQ=60°,
∴∠ABP=∠CBQ.
在△ABP和△CBQ中,
,
∴△ABP≌△CBQ(SAS),
∴AP=CQ.
(2)连接PQ,如图所示.
∵△ABP≌△CBQ,
∴∠BQC=∠BPA=150°.
∵BP=BQ,∠PBQ=60°,
∴△PBQ为等边三角形,
∴PQ=PB=8,∠BQP=60°,
∴∠PQC=90°.
在Rt△PQC中,∠PQC=90°,PQ=8,CQ=AP=6,
∴PC==10.
20.(1)证明见解析;(2);(3)
【详解】
(1)证明: ∵△ACB,△ECF都是等腰三角形,
∴CA=CB,CE=CF,∠ACB=∠ECF=90°,
∴∠ACE=∠BCF,
∴△AEC≌△BFC(SAS),
(2)解:∵CA=CB=6,∠ACB=90°,
∴,
∵△ACE≌△BCF,
∴∠CAD=∠DBF,
∵∠ADC=∠BDF,
∴∠ACD=∠DFB=90°,
∴
(3)如图,作FH⊥BC于H.
∠ACE=∠CAE=30°,
∴AE=EC,
∵△ACE≌△BCF,
∴BF=AE,CF=CE,
∴CF=BF,∠FCB=∠CBF=30°,
∵FC=FB,FH⊥BC,
∴CH=BH=3,
由
(负根舍去),,
∵∠CED=∠CAE+∠ACE=60°,∠ECD=90°﹣30°=60°,
∴△ECD是等边三角形,
∴,
∴.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
