湘教版 八下 3.2简单图形的坐标表示同步课时训练试卷(word版含答案)
文档属性
| 名称 | 湘教版 八下 3.2简单图形的坐标表示同步课时训练试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 537.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 15:33:00 | ||
图片预览




文档简介
3.2简单图形的坐标表示同步课时训练
一、单选题
1.在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )
A.1个 B.2个 C.3个 D.4个
2.在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:①f(x,y)=(y,x).如f(2,3)=(3,2);②g(x,y)=(﹣x,﹣y),如g(2,3)=(﹣2,﹣3).按照以上变换有:f(g(2,3))=f(﹣2,﹣3)=(﹣3,﹣2),那么g(f(﹣6,7))等于( ????)
A.(7,6) B.(7,﹣6) C.(﹣7,6) D.(﹣7,﹣6)
3.如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别为(0,0)、(4,0)、(2,4),则顶点C的坐标是( )
A.(4,6) B.(4,2) C.(6,4) D.(8,2)
4.在平面直角坐标系中,第一象限的点是( )
A.(﹣1,2) B.(1,3) C.(0,0) D.(2,﹣1)
5.经过点作直线,则直线( )
A.过点 B.平行于轴 C.经过原点 D.平行于轴
6.在平面直角坐标系中,点A(x,y)位于y轴正半轴,距离原点3个单位长度,则点A的坐标为( )
A.(3,0) B.(0,3) C.(﹣3,0) D.(0,﹣3)
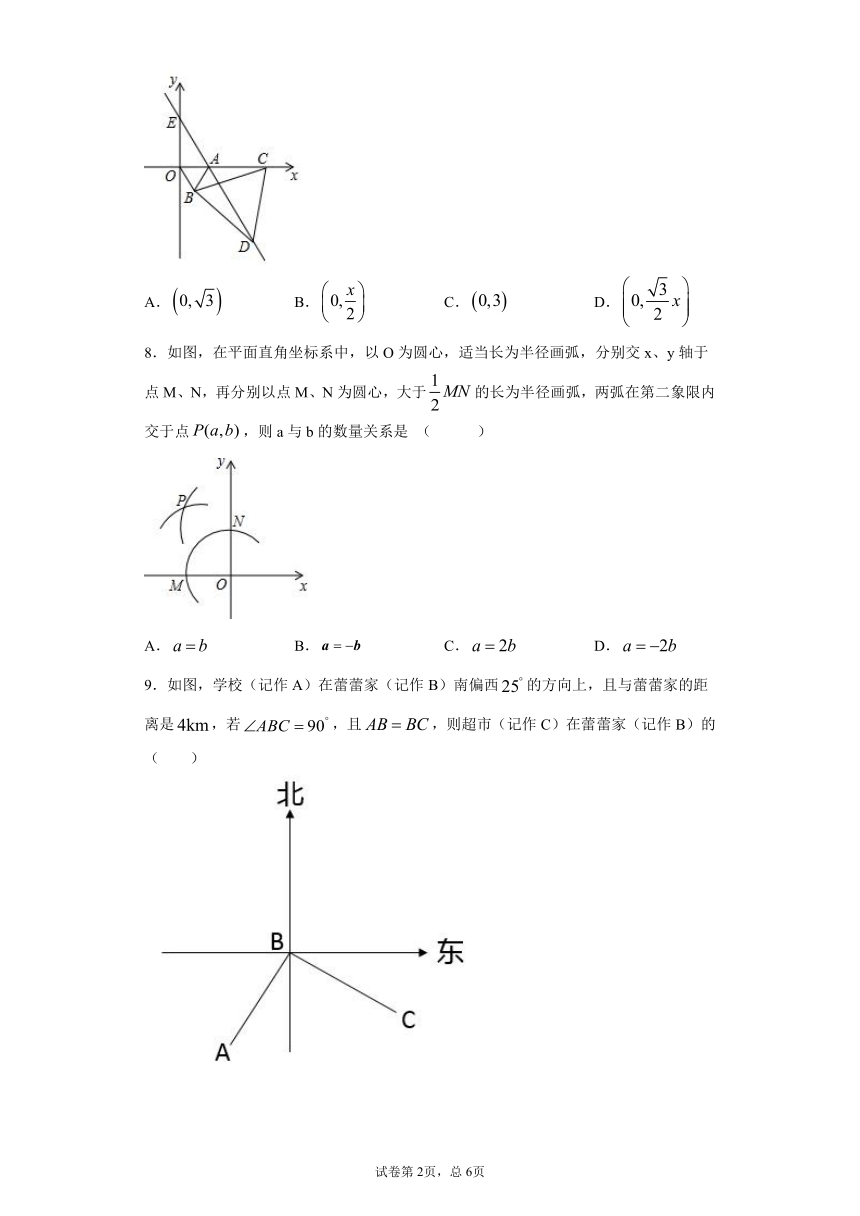
7.如图,在平面直角坐标系中,点的坐标为,以线段为边在第四象限内作等边,点为轴正半轴上一动点(),设点的坐标为,连结,以线段为边的第四象限内作等边,直线交轴于点,点的坐标是( )
A. B. C. D.
8.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,分别交x、y轴于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧在第二象限内交于点,则a与b的数量关系是 ( )
A. B. C. D.
9.如图,学校(记作A)在蕾蕾家(记作B)南偏西的方向上,且与蕾蕾家的距离是,若,且,则超市(记作C)在蕾蕾家(记作B)的( )
A.南偏东的方向上,相距 B.南偏东的方向上,相距
C.北偏东的方向上,相距 D.北偏东的方向上,相距
10.在平面直角坐标系中,已知点和点,经过点的直线轴,是直线上的一个动点,当线段的长度最短时,点的坐标为( )
A. B. C. D.
二、填空题
11.在平面直角坐标系中,有点,点,当线段轴,且时,则__.
12.已知点Q(2m2+4,2m2+m+6)在第一象限角平分线上,则m=________.
13.如图,A、B、C三点分别代表邮局、医院学校中的某一处,邮局和医院分别在学校的北偏西方向,邮局又在医院的北偏东方向,那么图中的点A应该是__________,点B应该是__________.
14.如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为_____.
15.平面直角坐标系上有点A(﹣3,4),则它到坐标原点的距离为_____.
16.如图,在平面直角坐标系中,,,以为直角边作,并使,再以为直角边作,并使,再以为直角边作,并使,…,按此规律进行下去,则的坐标是_______.
三、解答题
17.已知,,,且.
(1)如图1,求、、三点的坐标.
(2)如图2,延长至,连、,求.
(3)将线段平移,使点的对应点恰好落在轴正半轴上,点的对应点为,连交轴于,当时,求点的坐标.
18.在平面直角坐标系中,已知点A(),B(),其中满足.
(1)求点A,B的坐标;
(2)如图,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使CE=CB,连结BE交AD于点F,恰好有AF+AE=2,点G是CB上一点,且CG=1,连结FG,求证:EF=FG.
19.在平面直角坐标系中,已知A(x,y),且满足x2+6x+y2﹣6y+18=0,过点A作AB⊥y轴,垂足为B.
(1)求A点坐标;
(2)如图1,若分别以AB、AO为边作等边△ABC和等边△AOD,试判定线段AC和CD的数量关系和位置关系,并说明理由;
(3)如图2,若在x轴正半轴上取一点M,连接BM并延长至N,以BN为直角边作等腰Rt△BNE,∠BNE=90°,过点A作AF∥y轴交BE于点F,连接MF,设OM=a,MF=b,AF=c,试证明:.
20.如图,在平面直角坐标系中,点在轴上,点在第一象限,,,平分,,点,的横坐标分别为,,且.
(1)求的度数;
(2)求证:;
(3)设点的横坐标为,求证:.
参考答案
1.D
2.C
3.C
4.B
5.D
6.B
7.A
8.B
9.A
10.D
11.或0
12.-2
13.邮局 医院
14.
15.5
16.(,)
17.(1),,;(2)4;(3)或
【详解】
(1)∵,
又∵,,,
∴,,,
∴,,,
∴点,点,点.
(2)连接,如图1,
∵,,,,
∴,轴,,
∴,
,
,
,
∴
,
∴.
(3)①如图2,当,在原点同侧时,由平移性质可知,,
∴,
在和中,
,
∴≌(AAS),
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
②如图3,当,在原点两侧时,同理可证≌,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
综上的坐标为或.
18.(1)A(?1,1),B(1,?1);(2)见详解
【详解】
解:(1)∵,
∴m2+2mn+n2+n2?2n+1=0,
∴(m+n)2+(n?1)2=0,
∴m+n=0,n?1=0,
∴n=1,m=?1,
∴A(?1,1),B(1,?1);
(2)证明:如图,过点B作BH⊥AF交AF延长线于点H,连接EH,
∵点A的坐标为(?1,1),点B的坐标为(1,?1),
∴H(?1,?1),
∴AF+FH=2,
又∵AF+AE=2,
∴AE=FH,
又∵CG=1,AC=1,CE=CB,
∴AE=FH=BG,AH=BH=2,
∵AC⊥y轴,AD⊥x轴,BH⊥AH,
∴∠FHB=∠EAH=90°,
又∵AH=BH=2,
∴△EAH≌△FHB(SAS),
∴EH=FB,∠EHA=∠FBH,
∵CE=CB,
∴∠CEB=∠CBE,
又∵∠HBE=∠CEB,
∴∠HBE=∠EBC,
∴∠FBG=∠EHF,
在△EFH与△FBG中,
EH=FB,∠EHF=∠FBG,FH=BG,
∴△EFH≌△FBG(SAS),
∴EF=FG.
19.(1)点A的坐标为(﹣3,3);(2)CD=AC,CD⊥AC.理由见解析;(3)见解析.
【详解】
(1)∵x2+6x+y2﹣6y+18=0,
∴(x+3)2+(y﹣3)2=0,
∴x+3=0,y﹣3=0,
∴x=﹣3,y=3,
∴点A的坐标为(﹣3,3);
(2)CD=AC,CD⊥AC.
理由如下:
∵△ABC和△AOD为等边三角形,
∴AB=AC,AO=AD,∠DAO=∠CAB=60°,
∴∠DAO﹣∠CAO=∠CAB﹣∠CAO,
∴∠DAC=∠OAB,
∴△DAC≌△OAB(SAS),
∴CD=OB,∠ACD=∠ABO=90°,
由(1)可知BO=AB=3,
又∵AB=AC,
∴CD=OB=AB=AC,且CD⊥AC,
(3)证明:在AF上取一点P,使得AP=OM=a,连接BP,
∵AB=BO,AP=OM,∠PAB=∠MOB=90°,
∴△BAP≌△BOM(SAS),
∴∠ABP=∠OBM,BP=BM,
∵∠ABP+∠PBO=90°,
∴∠OBM+∠PBO=90°,
又∵△BEN为等腰直角三角形,
∴∠FBN=45°,
∴∠PBF=90°﹣45°=45°=∠FBN,
又∵BF=BF,
∴△FBP≌△FBM(SAS),
∴FP=FM=b,
∴AF=FP+AP,
即c=a+b.
∴ .
20.(1)60°;(2)见解析;(3)见解析
【详解】
解:(1),,
平分,
,
;
(2)如图,过点作轴于点,作于.
平分,
.
在和中,
.
;
(3)如图,作于,过点作轴于点.
平分,
.
在和中,
,
.
.
由(2)得,,
.
,
.
在中,,
.
.
,
,
.
一、单选题
1.在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )
A.1个 B.2个 C.3个 D.4个
2.在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:①f(x,y)=(y,x).如f(2,3)=(3,2);②g(x,y)=(﹣x,﹣y),如g(2,3)=(﹣2,﹣3).按照以上变换有:f(g(2,3))=f(﹣2,﹣3)=(﹣3,﹣2),那么g(f(﹣6,7))等于( ????)
A.(7,6) B.(7,﹣6) C.(﹣7,6) D.(﹣7,﹣6)
3.如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别为(0,0)、(4,0)、(2,4),则顶点C的坐标是( )
A.(4,6) B.(4,2) C.(6,4) D.(8,2)
4.在平面直角坐标系中,第一象限的点是( )
A.(﹣1,2) B.(1,3) C.(0,0) D.(2,﹣1)
5.经过点作直线,则直线( )
A.过点 B.平行于轴 C.经过原点 D.平行于轴
6.在平面直角坐标系中,点A(x,y)位于y轴正半轴,距离原点3个单位长度,则点A的坐标为( )
A.(3,0) B.(0,3) C.(﹣3,0) D.(0,﹣3)
7.如图,在平面直角坐标系中,点的坐标为,以线段为边在第四象限内作等边,点为轴正半轴上一动点(),设点的坐标为,连结,以线段为边的第四象限内作等边,直线交轴于点,点的坐标是( )
A. B. C. D.
8.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,分别交x、y轴于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧在第二象限内交于点,则a与b的数量关系是 ( )
A. B. C. D.
9.如图,学校(记作A)在蕾蕾家(记作B)南偏西的方向上,且与蕾蕾家的距离是,若,且,则超市(记作C)在蕾蕾家(记作B)的( )
A.南偏东的方向上,相距 B.南偏东的方向上,相距
C.北偏东的方向上,相距 D.北偏东的方向上,相距
10.在平面直角坐标系中,已知点和点,经过点的直线轴,是直线上的一个动点,当线段的长度最短时,点的坐标为( )
A. B. C. D.
二、填空题
11.在平面直角坐标系中,有点,点,当线段轴,且时,则__.
12.已知点Q(2m2+4,2m2+m+6)在第一象限角平分线上,则m=________.
13.如图,A、B、C三点分别代表邮局、医院学校中的某一处,邮局和医院分别在学校的北偏西方向,邮局又在医院的北偏东方向,那么图中的点A应该是__________,点B应该是__________.
14.如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为_____.
15.平面直角坐标系上有点A(﹣3,4),则它到坐标原点的距离为_____.
16.如图,在平面直角坐标系中,,,以为直角边作,并使,再以为直角边作,并使,再以为直角边作,并使,…,按此规律进行下去,则的坐标是_______.
三、解答题
17.已知,,,且.
(1)如图1,求、、三点的坐标.
(2)如图2,延长至,连、,求.
(3)将线段平移,使点的对应点恰好落在轴正半轴上,点的对应点为,连交轴于,当时,求点的坐标.
18.在平面直角坐标系中,已知点A(),B(),其中满足.
(1)求点A,B的坐标;
(2)如图,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使CE=CB,连结BE交AD于点F,恰好有AF+AE=2,点G是CB上一点,且CG=1,连结FG,求证:EF=FG.
19.在平面直角坐标系中,已知A(x,y),且满足x2+6x+y2﹣6y+18=0,过点A作AB⊥y轴,垂足为B.
(1)求A点坐标;
(2)如图1,若分别以AB、AO为边作等边△ABC和等边△AOD,试判定线段AC和CD的数量关系和位置关系,并说明理由;
(3)如图2,若在x轴正半轴上取一点M,连接BM并延长至N,以BN为直角边作等腰Rt△BNE,∠BNE=90°,过点A作AF∥y轴交BE于点F,连接MF,设OM=a,MF=b,AF=c,试证明:.
20.如图,在平面直角坐标系中,点在轴上,点在第一象限,,,平分,,点,的横坐标分别为,,且.
(1)求的度数;
(2)求证:;
(3)设点的横坐标为,求证:.
参考答案
1.D
2.C
3.C
4.B
5.D
6.B
7.A
8.B
9.A
10.D
11.或0
12.-2
13.邮局 医院
14.
15.5
16.(,)
17.(1),,;(2)4;(3)或
【详解】
(1)∵,
又∵,,,
∴,,,
∴,,,
∴点,点,点.
(2)连接,如图1,
∵,,,,
∴,轴,,
∴,
,
,
,
∴
,
∴.
(3)①如图2,当,在原点同侧时,由平移性质可知,,
∴,
在和中,
,
∴≌(AAS),
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
②如图3,当,在原点两侧时,同理可证≌,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
综上的坐标为或.
18.(1)A(?1,1),B(1,?1);(2)见详解
【详解】
解:(1)∵,
∴m2+2mn+n2+n2?2n+1=0,
∴(m+n)2+(n?1)2=0,
∴m+n=0,n?1=0,
∴n=1,m=?1,
∴A(?1,1),B(1,?1);
(2)证明:如图,过点B作BH⊥AF交AF延长线于点H,连接EH,
∵点A的坐标为(?1,1),点B的坐标为(1,?1),
∴H(?1,?1),
∴AF+FH=2,
又∵AF+AE=2,
∴AE=FH,
又∵CG=1,AC=1,CE=CB,
∴AE=FH=BG,AH=BH=2,
∵AC⊥y轴,AD⊥x轴,BH⊥AH,
∴∠FHB=∠EAH=90°,
又∵AH=BH=2,
∴△EAH≌△FHB(SAS),
∴EH=FB,∠EHA=∠FBH,
∵CE=CB,
∴∠CEB=∠CBE,
又∵∠HBE=∠CEB,
∴∠HBE=∠EBC,
∴∠FBG=∠EHF,
在△EFH与△FBG中,
EH=FB,∠EHF=∠FBG,FH=BG,
∴△EFH≌△FBG(SAS),
∴EF=FG.
19.(1)点A的坐标为(﹣3,3);(2)CD=AC,CD⊥AC.理由见解析;(3)见解析.
【详解】
(1)∵x2+6x+y2﹣6y+18=0,
∴(x+3)2+(y﹣3)2=0,
∴x+3=0,y﹣3=0,
∴x=﹣3,y=3,
∴点A的坐标为(﹣3,3);
(2)CD=AC,CD⊥AC.
理由如下:
∵△ABC和△AOD为等边三角形,
∴AB=AC,AO=AD,∠DAO=∠CAB=60°,
∴∠DAO﹣∠CAO=∠CAB﹣∠CAO,
∴∠DAC=∠OAB,
∴△DAC≌△OAB(SAS),
∴CD=OB,∠ACD=∠ABO=90°,
由(1)可知BO=AB=3,
又∵AB=AC,
∴CD=OB=AB=AC,且CD⊥AC,
(3)证明:在AF上取一点P,使得AP=OM=a,连接BP,
∵AB=BO,AP=OM,∠PAB=∠MOB=90°,
∴△BAP≌△BOM(SAS),
∴∠ABP=∠OBM,BP=BM,
∵∠ABP+∠PBO=90°,
∴∠OBM+∠PBO=90°,
又∵△BEN为等腰直角三角形,
∴∠FBN=45°,
∴∠PBF=90°﹣45°=45°=∠FBN,
又∵BF=BF,
∴△FBP≌△FBM(SAS),
∴FP=FM=b,
∴AF=FP+AP,
即c=a+b.
∴ .
20.(1)60°;(2)见解析;(3)见解析
【详解】
解:(1),,
平分,
,
;
(2)如图,过点作轴于点,作于.
平分,
.
在和中,
.
;
(3)如图,作于,过点作轴于点.
平分,
.
在和中,
,
.
.
由(2)得,,
.
,
.
在中,,
.
.
,
,
.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
