湘教版 八下 4.5一次函数的应用同步课时训练试卷(word版含答案)
文档属性
| 名称 | 湘教版 八下 4.5一次函数的应用同步课时训练试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 424.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览




文档简介
4.5一次函数的应用同步课时训练
一、单选题
1.已知直线与的交点的坐标为,则方程组的解是( )
A. B. C. D.
2.小甬,小真两人的跑步路程y(米)和跑步时间x(分)之间的关系如图所示,已知小甬的跑步速度比小真快,则下列说法正确的是( )
A.小甬每分钟跑200米.小真每分钟跑100米
B.小甬每跑100米时,小真只能跑60米
C.相遇时,小甬、小真两人都跑了500米
D.经过4分钟时,小甬、小真两人都跑800米
3.如图,一次函数y=kx+b(k,b为常数,且k≠0)的图象过点A(0,﹣1),B(1,1),则不等式kx+b>1的解集为( )
A.x>0 B.x<0 C.x>1 D.x<1
4.已知一次函数y1=kx+1(k<0)的图象与正比例函数y2=mx(m>0)的图象交于点(,),则不等式组的解集为( )
A. B. C. D.0<x<2
5.如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣1,0),B(4,0),则不等式(kx+b)(mx+n)>0的解集为( )
A.x>2 B.0<x<4 C.﹣1<x<4 D.x<﹣1或x>4
6.如图,直线和直线相交于点,根据图象可知,关于的方程的解是( )
A. B. C. D.
7.如图,已知一次函数y=kx+b的图象经过点A(﹣1,2)和点B(﹣2,0),一次函数y=mx的图象经过点A,则关于x的不等式组0<kx+b<mx的解集为( )
A.﹣2<x<﹣1 B.﹣1<x<0 C.x<﹣1 D.x>﹣1
8.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A. B. C. D.
9.下列关于一次函数y=﹣2x+2的图象的说法中,错误的是( )
A.函数图象经过第一、二、四象限
B.函数图象与x轴的交点坐标为(2,0)
C.当x>0时,y<2
D.y的值随着x值的增大而减小
10.一次函数与正比例函数,若,则自变量的取值范围是( )
A. B. C. D.
二、填空题
11.小明和小杰在同一直道的A,B两点间作匀速往返走锻炼(忽略掉头等时间).小明从A地出发,同时小杰从B地出发,两人第一次相遇时小明曾停下接电话数分钟.图中的折线表示从开始到小杰第一次到达A地止,两人之间的距离y(米)与行走时间x(分)的函数关系图象.则图中的________米,________分.
12.如图,在平面直角坐标系中,直线l1:y=ax+b(a、b为常数且a≠0)和直线l2:y=mx+n(m、n为常数且m≠0)相交于点A,若点A的坐标是(4,5),则关于x、y的二元一次方程组的解为_____.
13.一次函数y=ax+a+2的图象在﹣2≤x≤1的一段都在x轴的上方,那么a的取值范围是_____________.
14.如图,函数和的图象相交于点,点的纵坐标为40,则关于,的方程组的解是______.
15.如图,在平面直角坐标系中,A(2,0),B(0,1),AC=AB且AC⊥AB于点A,则OC所在直线的关系式是_____.
16.一次函数y=kx+b,(k,b为常数)的图象如图所示,则关于x的不等式kx+2b<0的解集是_____.
三、解答题
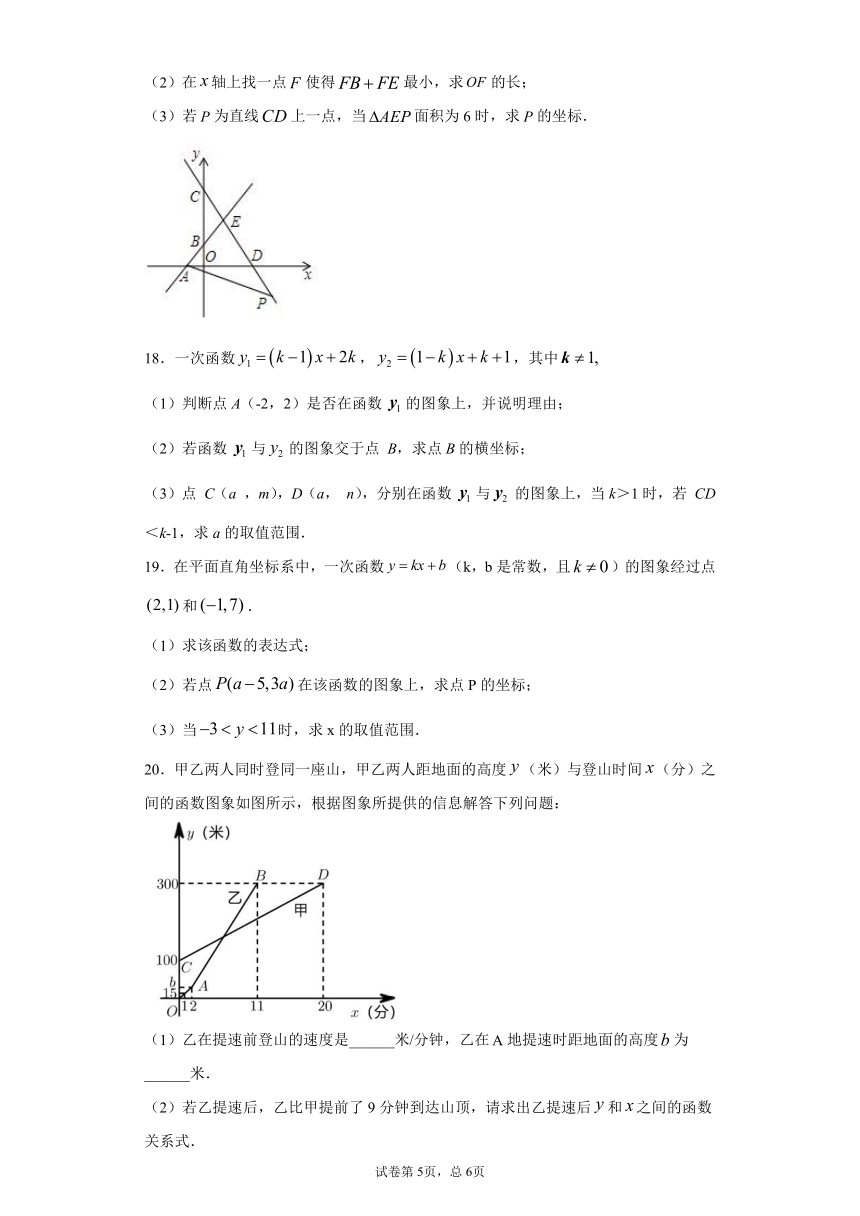
17.如图,直线与直线交于点.
(1)求点坐标;
(2)在轴上找一点使得最小,求的长;
(3)若为直线上一点,当面积为6时,求的坐标.
18.一次函数,,其中
(1)判断点A(-2,2)是否在函数的图象上,并说明理由;
(2)若函数与的图象交于点 B,求点B的横坐标;
(3)点 C(a ,m),D(a, n),分别在函数与的图象上,当k>1时,若 CD<k-1,求a的取值范围.
19.在平面直角坐标系中,一次函数(k,b是常数,且)的图象经过点和.
(1)求该函数的表达式;
(2)若点在该函数的图象上,求点P的坐标;
(3)当时,求x的取值范围.
20.甲乙两人同时登同一座山,甲乙两人距地面的高度(米)与登山时间(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)乙在提速前登山的速度是______米/分钟,乙在地提速时距地面的高度为______米.
(2)若乙提速后,乙比甲提前了9分钟到达山顶,请求出乙提速后和之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时甲距山顶的高度为多少米?
参考答案
1.A
2.B
3.C
4.A
5.C
6.A
7.A
8.C
9.B
10.A
11.3600 62.5
12.
13.﹣1<a<2且a≠0
14.
15.y=x.
16.x>6
17.(1);(2);(3),
【详解】
(1)联立,解得:,
∴;
(2)如图所示,将B沿着x轴对称至B1,
由直线AB的解析式可得:,则,
此时,连接B1E,与x轴交点即为所求F点,
设直线B1E的解析式为:,
将,代入得:
,解得:,
∴直线B1E的解析式为:,
令,解得:,
即:F的坐标为,
∴;
(3)由两直线解析式可得,,
,
①当P点在x轴下方时,,
即:,
则,
解得:或(舍去),
将代入,解得:,
∴;
②当P点在x轴上方时,,
即:,
则,
解得:或(舍去),
将代入,解得:,
∴;
综上,所有满足条件的P的坐标为,.
18.(1)在,见解析;(2)- ;(3)
【详解】
解:(1)在,理由如下
当x=-2时,,
故不论k为何值时,A(-2,2)始终在直线的图象上.
(2)令,
解得,
∵k≠1,
∴x=-,
∴点B的横坐标为-.
(3)将C(a ,m),D(a, n)分别代入,,可得:,,
∴,
解得:,
∵k>1,
∴k-1>0,
∴,
CD<k-1,
可得:,
解得.
19.(1);(2);(3).
【详解】
解:(1)一次函数过(2,1)和(-1,7),
∴,
解得:,
∴;
(2)由(1)可知:,
将代入,
∴,解得,
即,
∴;
(3)∵,
当时,
则,
解得:,
∴x的取值范围:.
20.(1)15;30;(2);(3)登山6.5分钟,乙追上了甲,此时甲距山顶的高度为135米
【详解】
(1)乙在提速前登山的速度是(米/分钟),乙在地提速时距地面的高度为(米).
(2),
设乙提速后的函数关系式为:,
∵图象经过,,
则,
解得:,,
所以乙提速后的关系式:.
(3)设甲的函数关系式为:,将点和点代入,则
,
解得:,,
甲的函数关系式为:;
由题意得:
解得:,,
相遇时甲距离山顶的高度为:(米),
答:登山6.5分钟,乙追上了甲,此时甲距离山顶的高度为135米.
一、单选题
1.已知直线与的交点的坐标为,则方程组的解是( )
A. B. C. D.
2.小甬,小真两人的跑步路程y(米)和跑步时间x(分)之间的关系如图所示,已知小甬的跑步速度比小真快,则下列说法正确的是( )
A.小甬每分钟跑200米.小真每分钟跑100米
B.小甬每跑100米时,小真只能跑60米
C.相遇时,小甬、小真两人都跑了500米
D.经过4分钟时,小甬、小真两人都跑800米
3.如图,一次函数y=kx+b(k,b为常数,且k≠0)的图象过点A(0,﹣1),B(1,1),则不等式kx+b>1的解集为( )
A.x>0 B.x<0 C.x>1 D.x<1
4.已知一次函数y1=kx+1(k<0)的图象与正比例函数y2=mx(m>0)的图象交于点(,),则不等式组的解集为( )
A. B. C. D.0<x<2
5.如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣1,0),B(4,0),则不等式(kx+b)(mx+n)>0的解集为( )
A.x>2 B.0<x<4 C.﹣1<x<4 D.x<﹣1或x>4
6.如图,直线和直线相交于点,根据图象可知,关于的方程的解是( )
A. B. C. D.
7.如图,已知一次函数y=kx+b的图象经过点A(﹣1,2)和点B(﹣2,0),一次函数y=mx的图象经过点A,则关于x的不等式组0<kx+b<mx的解集为( )
A.﹣2<x<﹣1 B.﹣1<x<0 C.x<﹣1 D.x>﹣1
8.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A. B. C. D.
9.下列关于一次函数y=﹣2x+2的图象的说法中,错误的是( )
A.函数图象经过第一、二、四象限
B.函数图象与x轴的交点坐标为(2,0)
C.当x>0时,y<2
D.y的值随着x值的增大而减小
10.一次函数与正比例函数,若,则自变量的取值范围是( )
A. B. C. D.
二、填空题
11.小明和小杰在同一直道的A,B两点间作匀速往返走锻炼(忽略掉头等时间).小明从A地出发,同时小杰从B地出发,两人第一次相遇时小明曾停下接电话数分钟.图中的折线表示从开始到小杰第一次到达A地止,两人之间的距离y(米)与行走时间x(分)的函数关系图象.则图中的________米,________分.
12.如图,在平面直角坐标系中,直线l1:y=ax+b(a、b为常数且a≠0)和直线l2:y=mx+n(m、n为常数且m≠0)相交于点A,若点A的坐标是(4,5),则关于x、y的二元一次方程组的解为_____.
13.一次函数y=ax+a+2的图象在﹣2≤x≤1的一段都在x轴的上方,那么a的取值范围是_____________.
14.如图,函数和的图象相交于点,点的纵坐标为40,则关于,的方程组的解是______.
15.如图,在平面直角坐标系中,A(2,0),B(0,1),AC=AB且AC⊥AB于点A,则OC所在直线的关系式是_____.
16.一次函数y=kx+b,(k,b为常数)的图象如图所示,则关于x的不等式kx+2b<0的解集是_____.
三、解答题
17.如图,直线与直线交于点.
(1)求点坐标;
(2)在轴上找一点使得最小,求的长;
(3)若为直线上一点,当面积为6时,求的坐标.
18.一次函数,,其中
(1)判断点A(-2,2)是否在函数的图象上,并说明理由;
(2)若函数与的图象交于点 B,求点B的横坐标;
(3)点 C(a ,m),D(a, n),分别在函数与的图象上,当k>1时,若 CD<k-1,求a的取值范围.
19.在平面直角坐标系中,一次函数(k,b是常数,且)的图象经过点和.
(1)求该函数的表达式;
(2)若点在该函数的图象上,求点P的坐标;
(3)当时,求x的取值范围.
20.甲乙两人同时登同一座山,甲乙两人距地面的高度(米)与登山时间(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)乙在提速前登山的速度是______米/分钟,乙在地提速时距地面的高度为______米.
(2)若乙提速后,乙比甲提前了9分钟到达山顶,请求出乙提速后和之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时甲距山顶的高度为多少米?
参考答案
1.A
2.B
3.C
4.A
5.C
6.A
7.A
8.C
9.B
10.A
11.3600 62.5
12.
13.﹣1<a<2且a≠0
14.
15.y=x.
16.x>6
17.(1);(2);(3),
【详解】
(1)联立,解得:,
∴;
(2)如图所示,将B沿着x轴对称至B1,
由直线AB的解析式可得:,则,
此时,连接B1E,与x轴交点即为所求F点,
设直线B1E的解析式为:,
将,代入得:
,解得:,
∴直线B1E的解析式为:,
令,解得:,
即:F的坐标为,
∴;
(3)由两直线解析式可得,,
,
①当P点在x轴下方时,,
即:,
则,
解得:或(舍去),
将代入,解得:,
∴;
②当P点在x轴上方时,,
即:,
则,
解得:或(舍去),
将代入,解得:,
∴;
综上,所有满足条件的P的坐标为,.
18.(1)在,见解析;(2)- ;(3)
【详解】
解:(1)在,理由如下
当x=-2时,,
故不论k为何值时,A(-2,2)始终在直线的图象上.
(2)令,
解得,
∵k≠1,
∴x=-,
∴点B的横坐标为-.
(3)将C(a ,m),D(a, n)分别代入,,可得:,,
∴,
解得:,
∵k>1,
∴k-1>0,
∴,
CD<k-1,
可得:,
解得.
19.(1);(2);(3).
【详解】
解:(1)一次函数过(2,1)和(-1,7),
∴,
解得:,
∴;
(2)由(1)可知:,
将代入,
∴,解得,
即,
∴;
(3)∵,
当时,
则,
解得:,
∴x的取值范围:.
20.(1)15;30;(2);(3)登山6.5分钟,乙追上了甲,此时甲距山顶的高度为135米
【详解】
(1)乙在提速前登山的速度是(米/分钟),乙在地提速时距地面的高度为(米).
(2),
设乙提速后的函数关系式为:,
∵图象经过,,
则,
解得:,,
所以乙提速后的关系式:.
(3)设甲的函数关系式为:,将点和点代入,则
,
解得:,,
甲的函数关系式为:;
由题意得:
解得:,,
相遇时甲距离山顶的高度为:(米),
答:登山6.5分钟,乙追上了甲,此时甲距离山顶的高度为135米.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
