湘教版 九下 2.7正多边形与圆同步课时训练试卷(word版含答案)
文档属性
| 名称 | 湘教版 九下 2.7正多边形与圆同步课时训练试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 290.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 15:47:34 | ||
图片预览


文档简介
2.7正多边形与圆同步课时训练
一、单选题
1.如图所示,为的内接三角形,,则的内接正方形的面积( )
A. B. C. D.
2.如图,两个正六边形ABCDEF、EDGHIJ的顶点A、B、H、I在同一个圆上,点P在上,则tan∠API的值是( )
A.2 B.2 C.2 D.1
3.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2 B.2 C. D.4
4.已知正六边形内接于,若的直径为,则该正六边形的周长是( )
A. B. C. D.
5.如图,有一个半径为的圆形纸片,若在该纸片上沿虚线剪一个最大正六边形纸片,则这个正六边形纸片的边心距是( ).
A. B. C. D.
6.正多边形的内切圆与外接圆的半径之比为,则这个正多边形为( )
A.正十二边形 B.正六边形 C.正四边形 D.正三角形
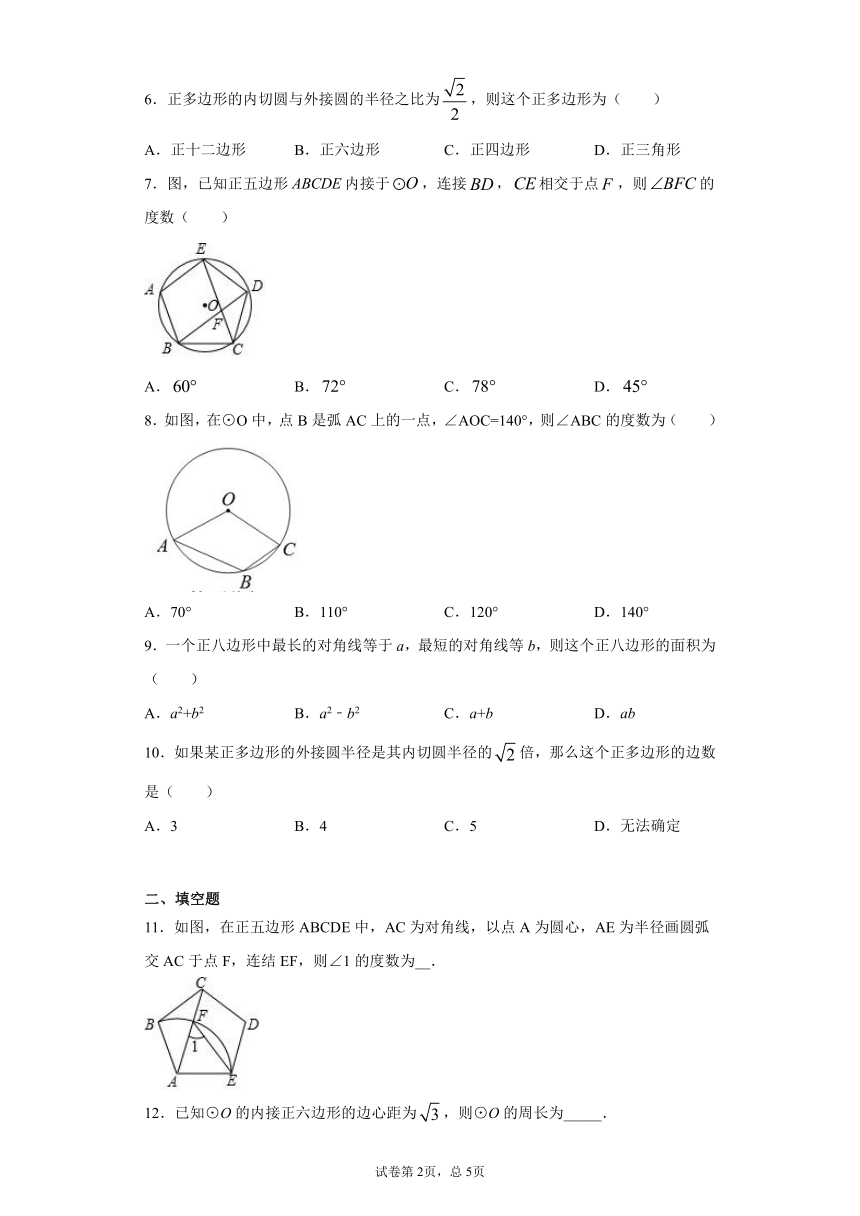
7.图,已知正五边形内接于,连接,相交于点,则的度数( )
A. B. C. D.
8.如图,在⊙O中,点B是弧AC上的一点,∠AOC=140°,则∠ABC的度数为( )
A.70° B.110° C.120° D.140°
9.一个正八边形中最长的对角线等于a,最短的对角线等b,则这个正八边形的面积为( )
A.a2+b2 B.a2﹣b2 C.a+b D.ab
10.如果某正多边形的外接圆半径是其内切圆半径的倍,那么这个正多边形的边数是( )
A.3 B.4 C.5 D.无法确定
二、填空题
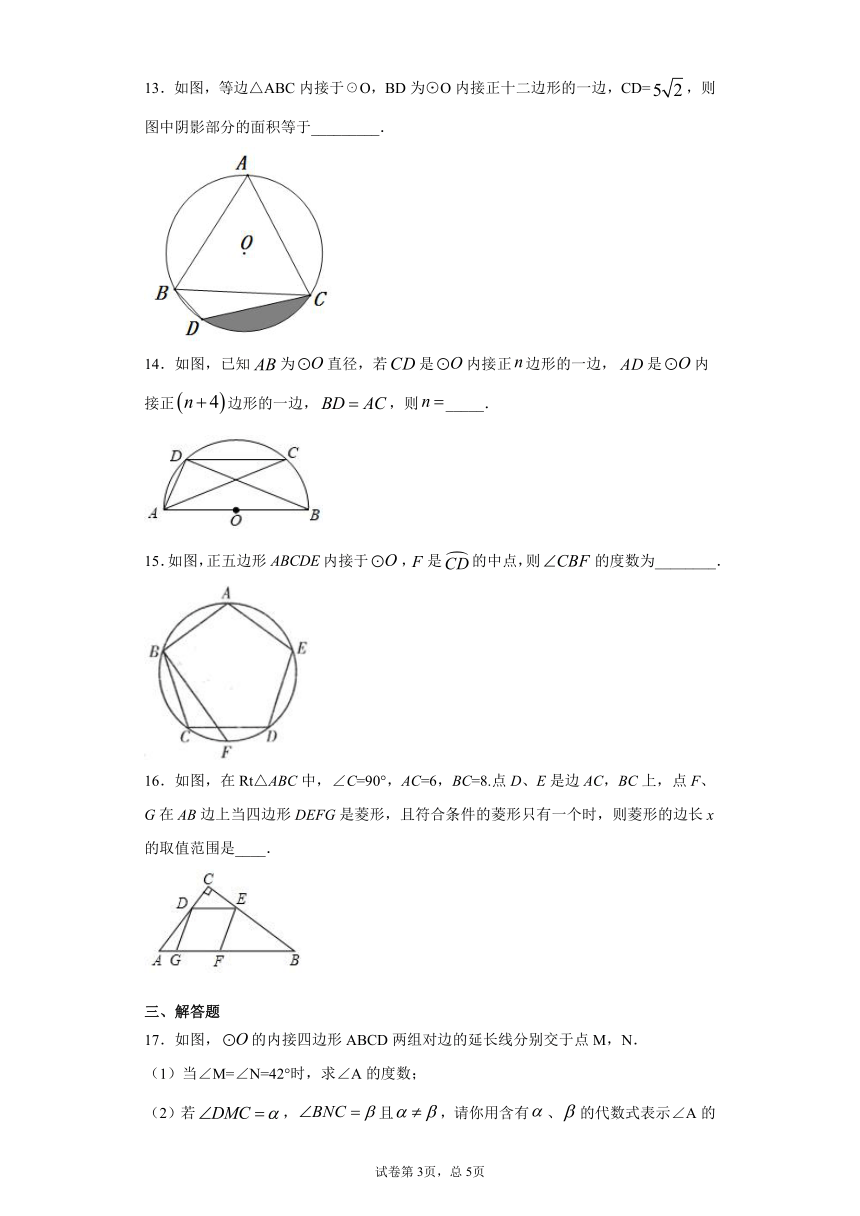
11.如图,在正五边形ABCDE中,AC为对角线,以点A为圆心,AE为半径画圆弧交AC于点F,连结EF,则∠1的度数为__.
12.已知⊙O的内接正六边形的边心距为,则⊙O的周长为_____.
13.如图,等边△ABC内接于☉O,BD为⊙O内接正十二边形的一边,CD=,则图中阴影部分的面积等于_________.
14.如图,已知为直径,若是内接正边形的一边,是内接正边形的一边,,则_____.
15.如图,正五边形内接于,是的中点,则的度数为________.
16.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.点D、E是边AC,BC上,点F、G在AB边上当四边形DEFG是菱形,且符合条件的菱形只有一个时,则菱形的边长x的取值范围是____.
三、解答题
17.如图,的内接四边形ABCD两组对边的延长线分别交于点M,N.
(1)当∠M=∠N=42°时,求∠A的度数;
(2)若,且,请你用含有、的代数式表示∠A的度数.
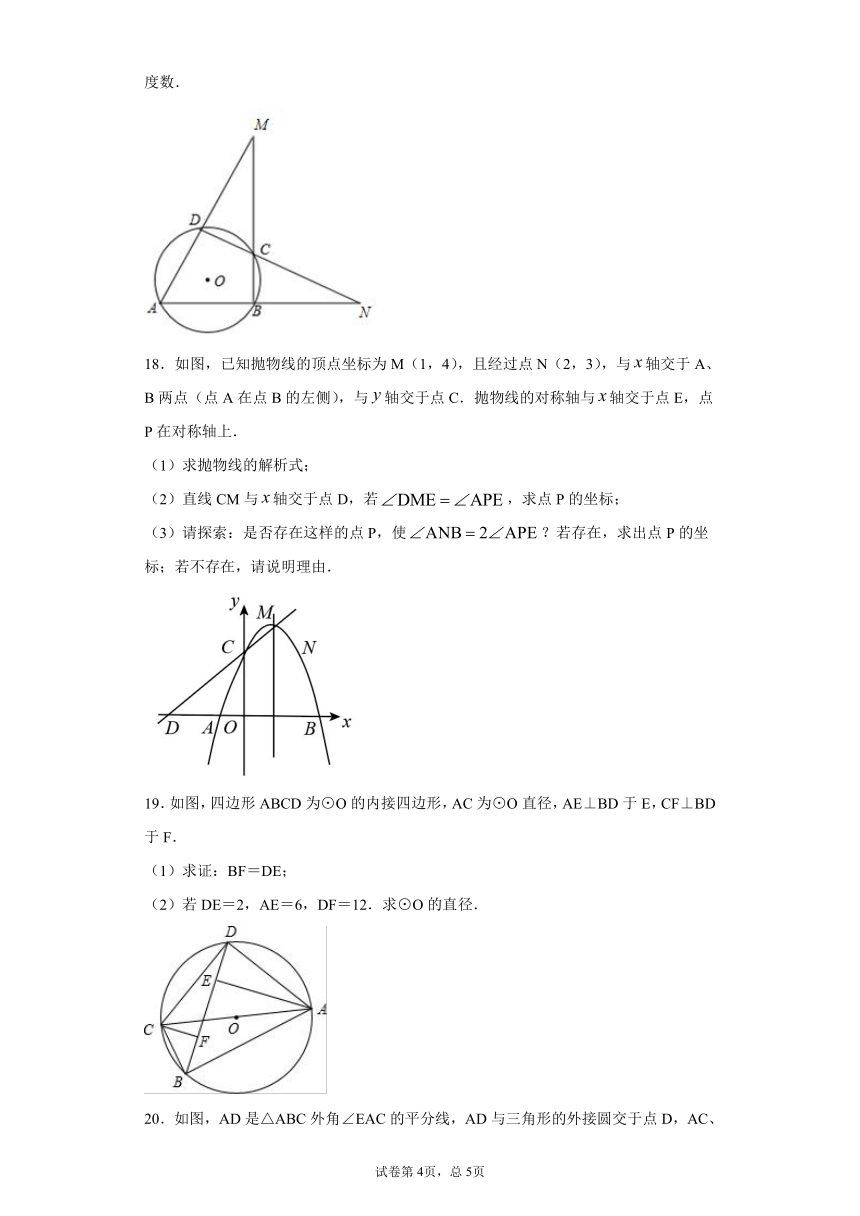
18.如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与轴交于A、B两点(点A在点B的左侧),与轴交于点C.抛物线的对称轴与轴交于点E,点P在对称轴上.
(1)求抛物线的解析式;
(2)直线CM与轴交于点D,若,求点P的坐标;
(3)请探索:是否存在这样的点P,使?若存在,求出点P的坐标;若不存在,请说明理由.
19.如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
(1)求证:BF=DE;
(2)若DE=2,AE=6,DF=12.求⊙O的直径.
20.如图,AD是△ABC外角∠EAC的平分线,AD与三角形的外接圆交于点D,AC、BD相交于点P.
求证:(1)△DBC为等腰三角形;
(2)AB∶BD=PB∶PC.
参考答案
1.C
2.A
3.A
4.C
5.C
6.C
7.B
8.B
9.D
10.B
11.54°
12.4π
13.
14.
15.
16.或
17.(1)∠A=48°;(2)∠A=90°.
【详解】
解:(1)在△CDM与△CBN中,∵∠M=∠N=42°,∠MCD=∠NCB,
∴∠CDM=∠CBN,
∴180°-∠CDM=180°-∠CBN,即∠ADC=∠ABC,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠ABC=90°;
∵∠M =42°,
∴∠A=90°-∠M=48°;
(2)∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠MDC+∠NBC=180°,
∵∠M+∠MDC+∠MCD=180°,∠N+∠NCB+∠NBC=180°,
∴∠M+∠N+∠MCD+∠NCB=180°,
又,
∴∠MCD+∠NCB=180°-(α+β),
∴∠BCD+∠NCM=360°-(∠MCD+∠NCB)=180°+(α+β),
∵∠BCD=∠NCM,
∴∠BCD=90°+,
∵∠A+∠BCD=180°,
∴∠A=90°-;
18.(1)y=-x2+2x+3;(2)P(1,2)或(1,-2);(3)P(1,+1)或(1,--1).
【详解】
解:(1)设抛物线为y=a(x-1)2+4.
∵抛物线过点(2,3)
∴3=a(2-1)2+4,解得a=-1
∴抛物线的解析式为y=-(x-1)2+4,即y=-x2+2x+3;
(2)如图1,令y=0,则-(x-1)2+4=0,解得x=-1或x=3,
∴A(-1,0),B(3,0),
令x=0,可得y=3
∴C(0,3),
∵M(1,4)
∴运用待定系数法可得:直线CM的解析式为y=x+3
令y=0,则x+3=0,x=-3,
∴D(-3,0)
∵∠DEM=∠AEP=90°,∠DMB=∠APE.
∴△DEM∽△AEP,
∴
∵A(-1,0),E(1,0),D(-3,0),M(1,4).
∴DE=4,ME=4,AE=2.
∴,即PE=2
∴P(1,2)或(1,-2);
(3)存在,P的坐标为(1,+1)或(1,--1),理由如下:
如图2,①当点P在x轴上方时,连接BP,
∵PE是抛物线的对称轴,
∴∠APE=∠BPE,∠APB=2∠APE
∵∠ANB=2∠APE
∴∠ANB=∠APB
∴点A,B,N,P四点共圆,
设圆心F的坐标为(1,n),即PF=AF=NF,
∵A(-1,0),N(2,3)
∴
∴n2+4=1+(3-n)2,解得n=1
∴F(1,1),即PF=AF=
∴PE=+1,P(1,+1);
②当点P在x轴下方时,由对称知,P(1,--1);
综上,点P的坐标为P(1,+1)或(1,--1).
19.(1)证明见解析;(2)圆的直径为10.
【详解】
(1)证明:延长CF交⊙O于H,连接AH,作OM⊥BD于M,延长MO交AH于N,如图,
∵OM⊥BD,
∴BM=DM,
∵AC为直径,
∴∠AHC=90°,
∵AE⊥BD于E,CF⊥BD,
∴四边形AHFE为矩形,MN∥AE∥FH,
∵ON∥CH,点O为AC的中点,
∴点N为AH的中点,
∴M点为EF的中点,
∴FM=EM,
∴BM﹣FM=DM﹣EM,
即BF=DE;
(2)解:易得四边形ANME为矩形,则MN=AE=6,
∵DE=2,DF=12,
∴BF=2,EF=12﹣2=10,BE=12,
∴AH=EF=10,
在Rt△ADE中,AD2,
在Rt△ABE中,AB6,
∵AC为直径,
∴∠ABC=90°,
∵∠ACB=∠ADE,
∴Rt△ACB∽Rt△ADE,
∴,即,
解得:AC=10,
即圆的直径为10.
20.(1)见解析;(2)见解析.
【详解】
证明:(1)∵AD是∠EAC的平分线,
∴∠EAD=∠DAC,
∵∠EAD是圆内接四边形ABCD的外角,
∴∠EAD=∠DCB,
∵∠DAC=∠DBC,
∴∠DCB=∠DBC,
∴BD=DC,
∴△DBC为等腰三角形;
(2)在△ABP和△DCP中,
∵∠BAP=∠CDP,∠APB=∠DPC,
∴△ABP∽△DCP,
∴AB:DC=PB:PC,
∵BD=DC,
∴AB:BD=PB:PC.
一、单选题
1.如图所示,为的内接三角形,,则的内接正方形的面积( )
A. B. C. D.
2.如图,两个正六边形ABCDEF、EDGHIJ的顶点A、B、H、I在同一个圆上,点P在上,则tan∠API的值是( )
A.2 B.2 C.2 D.1
3.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2 B.2 C. D.4
4.已知正六边形内接于,若的直径为,则该正六边形的周长是( )
A. B. C. D.
5.如图,有一个半径为的圆形纸片,若在该纸片上沿虚线剪一个最大正六边形纸片,则这个正六边形纸片的边心距是( ).
A. B. C. D.
6.正多边形的内切圆与外接圆的半径之比为,则这个正多边形为( )
A.正十二边形 B.正六边形 C.正四边形 D.正三角形
7.图,已知正五边形内接于,连接,相交于点,则的度数( )
A. B. C. D.
8.如图,在⊙O中,点B是弧AC上的一点,∠AOC=140°,则∠ABC的度数为( )
A.70° B.110° C.120° D.140°
9.一个正八边形中最长的对角线等于a,最短的对角线等b,则这个正八边形的面积为( )
A.a2+b2 B.a2﹣b2 C.a+b D.ab
10.如果某正多边形的外接圆半径是其内切圆半径的倍,那么这个正多边形的边数是( )
A.3 B.4 C.5 D.无法确定
二、填空题
11.如图,在正五边形ABCDE中,AC为对角线,以点A为圆心,AE为半径画圆弧交AC于点F,连结EF,则∠1的度数为__.
12.已知⊙O的内接正六边形的边心距为,则⊙O的周长为_____.
13.如图,等边△ABC内接于☉O,BD为⊙O内接正十二边形的一边,CD=,则图中阴影部分的面积等于_________.
14.如图,已知为直径,若是内接正边形的一边,是内接正边形的一边,,则_____.
15.如图,正五边形内接于,是的中点,则的度数为________.
16.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.点D、E是边AC,BC上,点F、G在AB边上当四边形DEFG是菱形,且符合条件的菱形只有一个时,则菱形的边长x的取值范围是____.
三、解答题
17.如图,的内接四边形ABCD两组对边的延长线分别交于点M,N.
(1)当∠M=∠N=42°时,求∠A的度数;
(2)若,且,请你用含有、的代数式表示∠A的度数.
18.如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与轴交于A、B两点(点A在点B的左侧),与轴交于点C.抛物线的对称轴与轴交于点E,点P在对称轴上.
(1)求抛物线的解析式;
(2)直线CM与轴交于点D,若,求点P的坐标;
(3)请探索:是否存在这样的点P,使?若存在,求出点P的坐标;若不存在,请说明理由.
19.如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
(1)求证:BF=DE;
(2)若DE=2,AE=6,DF=12.求⊙O的直径.
20.如图,AD是△ABC外角∠EAC的平分线,AD与三角形的外接圆交于点D,AC、BD相交于点P.
求证:(1)△DBC为等腰三角形;
(2)AB∶BD=PB∶PC.
参考答案
1.C
2.A
3.A
4.C
5.C
6.C
7.B
8.B
9.D
10.B
11.54°
12.4π
13.
14.
15.
16.或
17.(1)∠A=48°;(2)∠A=90°.
【详解】
解:(1)在△CDM与△CBN中,∵∠M=∠N=42°,∠MCD=∠NCB,
∴∠CDM=∠CBN,
∴180°-∠CDM=180°-∠CBN,即∠ADC=∠ABC,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠ABC=90°;
∵∠M =42°,
∴∠A=90°-∠M=48°;
(2)∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠MDC+∠NBC=180°,
∵∠M+∠MDC+∠MCD=180°,∠N+∠NCB+∠NBC=180°,
∴∠M+∠N+∠MCD+∠NCB=180°,
又,
∴∠MCD+∠NCB=180°-(α+β),
∴∠BCD+∠NCM=360°-(∠MCD+∠NCB)=180°+(α+β),
∵∠BCD=∠NCM,
∴∠BCD=90°+,
∵∠A+∠BCD=180°,
∴∠A=90°-;
18.(1)y=-x2+2x+3;(2)P(1,2)或(1,-2);(3)P(1,+1)或(1,--1).
【详解】
解:(1)设抛物线为y=a(x-1)2+4.
∵抛物线过点(2,3)
∴3=a(2-1)2+4,解得a=-1
∴抛物线的解析式为y=-(x-1)2+4,即y=-x2+2x+3;
(2)如图1,令y=0,则-(x-1)2+4=0,解得x=-1或x=3,
∴A(-1,0),B(3,0),
令x=0,可得y=3
∴C(0,3),
∵M(1,4)
∴运用待定系数法可得:直线CM的解析式为y=x+3
令y=0,则x+3=0,x=-3,
∴D(-3,0)
∵∠DEM=∠AEP=90°,∠DMB=∠APE.
∴△DEM∽△AEP,
∴
∵A(-1,0),E(1,0),D(-3,0),M(1,4).
∴DE=4,ME=4,AE=2.
∴,即PE=2
∴P(1,2)或(1,-2);
(3)存在,P的坐标为(1,+1)或(1,--1),理由如下:
如图2,①当点P在x轴上方时,连接BP,
∵PE是抛物线的对称轴,
∴∠APE=∠BPE,∠APB=2∠APE
∵∠ANB=2∠APE
∴∠ANB=∠APB
∴点A,B,N,P四点共圆,
设圆心F的坐标为(1,n),即PF=AF=NF,
∵A(-1,0),N(2,3)
∴
∴n2+4=1+(3-n)2,解得n=1
∴F(1,1),即PF=AF=
∴PE=+1,P(1,+1);
②当点P在x轴下方时,由对称知,P(1,--1);
综上,点P的坐标为P(1,+1)或(1,--1).
19.(1)证明见解析;(2)圆的直径为10.
【详解】
(1)证明:延长CF交⊙O于H,连接AH,作OM⊥BD于M,延长MO交AH于N,如图,
∵OM⊥BD,
∴BM=DM,
∵AC为直径,
∴∠AHC=90°,
∵AE⊥BD于E,CF⊥BD,
∴四边形AHFE为矩形,MN∥AE∥FH,
∵ON∥CH,点O为AC的中点,
∴点N为AH的中点,
∴M点为EF的中点,
∴FM=EM,
∴BM﹣FM=DM﹣EM,
即BF=DE;
(2)解:易得四边形ANME为矩形,则MN=AE=6,
∵DE=2,DF=12,
∴BF=2,EF=12﹣2=10,BE=12,
∴AH=EF=10,
在Rt△ADE中,AD2,
在Rt△ABE中,AB6,
∵AC为直径,
∴∠ABC=90°,
∵∠ACB=∠ADE,
∴Rt△ACB∽Rt△ADE,
∴,即,
解得:AC=10,
即圆的直径为10.
20.(1)见解析;(2)见解析.
【详解】
证明:(1)∵AD是∠EAC的平分线,
∴∠EAD=∠DAC,
∵∠EAD是圆内接四边形ABCD的外角,
∴∠EAD=∠DCB,
∵∠DAC=∠DBC,
∴∠DCB=∠DBC,
∴BD=DC,
∴△DBC为等腰三角形;
(2)在△ABP和△DCP中,
∵∠BAP=∠CDP,∠APB=∠DPC,
∴△ABP∽△DCP,
∴AB:DC=PB:PC,
∵BD=DC,
∴AB:BD=PB:PC.
