7.3 万有引力理论的成就—2020-2021学年【新教材】人教版(2019)高中物理必修二课件(31张PPT)
文档属性
| 名称 | 7.3 万有引力理论的成就—2020-2021学年【新教材】人教版(2019)高中物理必修二课件(31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览








文档简介
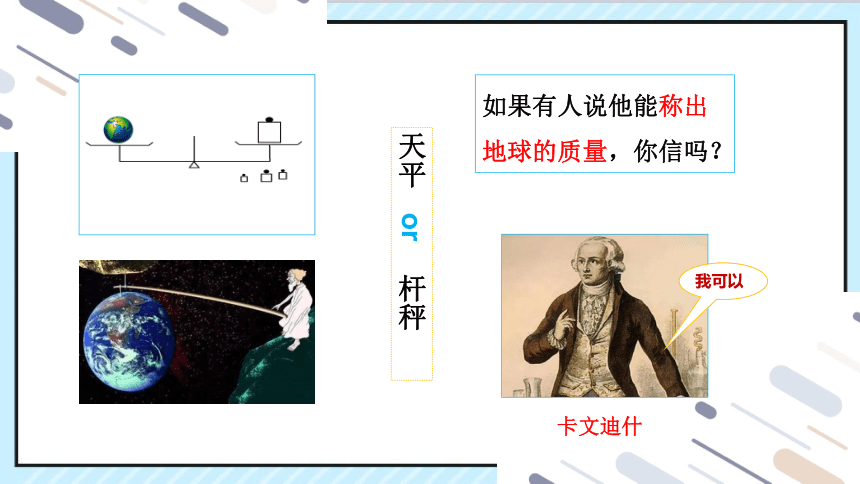
阿基米德在研究杠杆原理后,曾经说过一句什么名言?
“给我一个支点,我可以撬动地球。”
那给我们一个天平是否就可以称量地球的质量了呢?
不能
如果有人说他能称出地球的质量,你信吗?
我可以
天平 or 杆秤
卡文迪什
第七章 万有引力与宇宙航行
7.3 万有引力理论的成就
M=
若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的引力
卡文迪什
被称为能称出地球质量的人
GM=gR2
一、“称量”地球的质量
黄金代换公式
例题1:地球的质量到底有多大?已知:地球表面g=9.8m/s2,地球半径R=6400km,引力常量G=6.67×10-11Nm2/kg2。请你根据这些数据计算地球的质量。
M=6.0×1024kg
M=
如果测出了某行星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?
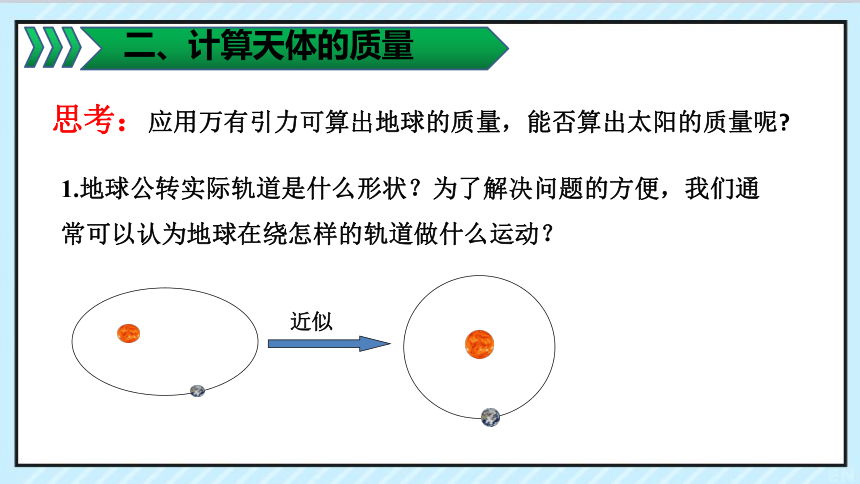
思考:应用万有引力可算出地球的质量,能否算出太阳的质量呢?
1.地球公转实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
近似
二、计算天体的质量
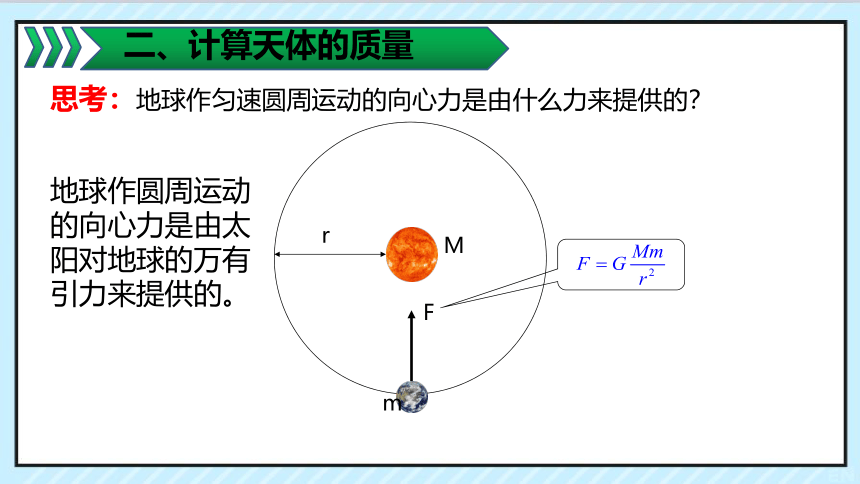
思考:地球作匀速圆周运动的向心力是由什么力来提供的?
r
M
m
F
地球作圆周运动的向心力是由太阳对地球的万有引力来提供的。
二、计算天体的质量
【注意】行星绕太阳做匀速圆周运动,向心力是由它们之间的万有引力提供的,即Fn=F万
二、计算天体的质量
r
M
m
F
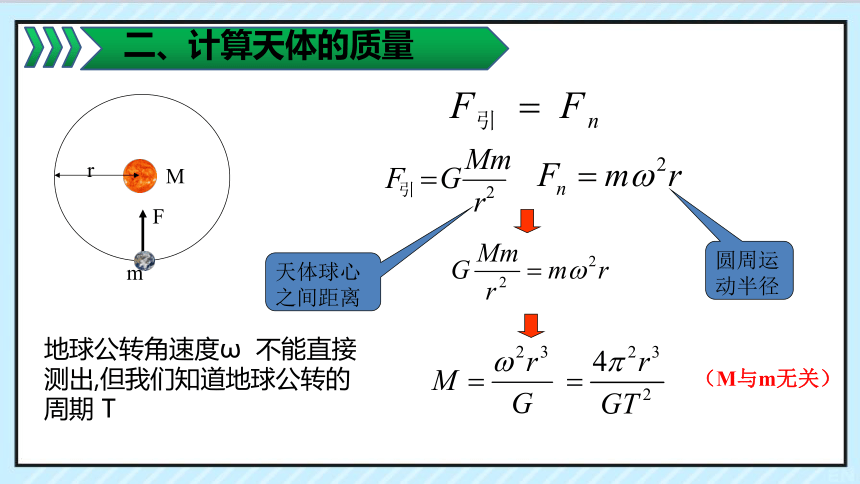
地球公转角速度ω 不能直接测出,但我们知道地球公转的周期 T
(M与m无关)
二、计算天体的质量
天体球心之间距离
圆周运动半径
中心天体M
环绕天体m
求解思路:
环行天体的向心力由中心天体对其万有引力独家提供
具体方法:
二、计算天体的质量
注意:只能求解中心天体质量
中心天体M
环绕天体m
二、计算天体的质量
注意:只能求解中心天体质量
思考:如何求解环绕天体质量?
把环绕天体变成中心天体
思考:如何把环绕天体变成中心天体?
发射一颗卫星绕其运动测出卫星周期T、转动半径r即可。
拓展:利用月球求地球质量
月球绕地球运行的周期T=27.3天,月球与地球的平均距离r=3.84×108m
M地=5.98×1024kg
二、计算天体的质量
已知太阳与地球间的平均距离约为1.5x1011m,你能估算太阳的质量吗?换用其他行星的相关数据进行估算,结果会相近吗?为什么?
解:地球绕太阳运转的周期:
T=365×24×60×60s=3.15×107s
地球绕太阳做匀速圆周运动的向心力由万有引力提供,
虽然不同行星与太阳间的距离r和绕太阳公转的周期T 各不相同,但是根据开普勒第三定律,所有行星的 均相同,所以无论选择哪颗行星的轨道半径和公转周期进行计算,所得的太阳质量均相同。
已知引力常量G、月球中心到地球中心的距离r和月球绕地球运行的
周期T。仅利用这三个数据,可以估算出的物理量有( )
A.月球的质量 B.地球的质量
C.地球的半径 D.月球绕地球运行速度的大小
BD
【针对训练】
天体质量和密度的两种思路
1.重力加速度法:在天体表面,重力近似等于万有引力
M=
三、计算天体的密度
天体的体积:
2.环绕法:万有引力提供向心力F引=Fn
①已知环绕天体运动的轨道半径r、速度V、引力常量G,中心天体半径R
三、计算天体的密度
注意:r为环绕天体运动的轨道半径,R为中心天体的半径
2.环绕法:
①已知环绕天体运动的轨道半径r、速度V、引力常量G,中心天体半径R
三、计算天体的密度
②已知环绕天体运动的轨道半径r、角速度ω、引力常量G,中心天体半径R
③已知环绕天体运动的轨道半径r、周期T、引力常量G,中心天体半径R
④已知环绕天体运动的速度v、周期T、引力常量G,中心天体半径R
如何列式求解?
2.环绕法:
②已知环绕天体运动的轨道半径r、角速度ω、引力常量G,中心天体半径R
三、计算天体的密度
注意:r为环绕天体运动的轨道半径,R为中心天体的半径
2.环绕法:
③已知环绕天体运动的轨道半径r、周期T、引力常量G,中心天体半径R
注意:r为环绕天体运动的轨道半径,R为中心天体的半径
三、计算天体的密度
2.环绕法:
④已知环绕天体运动的速度v、周期T、引力常量G,中心天体半径R
注意:R为中心天体的半径
三、计算天体的密度
思考:如何求解r?
?
重力加速度法
环绕法
情景
已知天体(如地球)的半径R和天体(如地球)表面的重力加速度g
行星或卫星绕中心
天体做匀速圆周运动
思路
物体在表面的重力近似等于天体(如地球)与物体间的万有引力:
行星或卫星受到的万有引力充当向心力:
天体质量
天体(如地球)质量:
中心天体质量:
天体密度
?
?
说明
g为天体表面重力加速度,未知星球表面重力加速度通常利用实验测出,例如让小球做自由落体、平抛、上抛等运动
这种方法只能求中心天体质量,不能求卫星质量,T为公转周期r为轨道半径
R为中心天体半径
【针对训练】
宇航员为测量某一星球的质量,在该星球表面用弹簧测力计称得质量为m的物体,弹簧测力计示数为F,已知星球半径为R,引力常量为G,不考虑星球自转,求该星球质量M?
F引=G?
忽略星球自转
【针对训练】
课本P58面第1题
到了 18 世纪,人们已经知道太阳系有 7 颗行星,其中1781 年发现的第七颗行星 —— 天王星的运动轨道有些“古怪”:根据万有引力定律计算出来的轨道与实际观测的结果总有一些偏差。
?是天文观测数据不准确?
?是万有引力定律的准确性有问题?
?是天王星轨道外面还有一颗未发现的行星?
四、发现未知天体
英国剑桥大学的学生亚当斯和法国年轻的天文学家勒维耶相信未知行星的存在。他们根据天王星的观测资料,各自独立地利用万有引力定律计算出这颗“新”行星的轨道。1846 年 9 月 23 日晚,德国的伽勒在勒维耶预言的位置附近发现了这颗行星,人们称其为“笔尖下发现的行星”。后来,这颗行星被命名为海王星(图 7.3-2)。海王星的发现过程充分显示了理论对于实践的巨大指导作用,所用的“计算预测和观察”的方法指导人们寻找新的天体。
理论轨道
实际轨道
海王星发现之后,人们发现它的轨道也与理论计算的不一致。于是几位学者用亚当斯和勒维耶列的方法预言另一颗行星的存在。
在预言提出之后,1930年3月14日,汤博发现了这颗行
星——冥王星。
哈雷依据万有引力定律,用一年时间计算了它们的轨道。发现 1531 年、1607 年和 1682 年出现的这三颗彗星轨道看起来如出一辙,他大胆预言,这三次出现的彗星是同一颗星(图 7.3-3),周期约为 76 年,并预言它将于 1758 年底或 1759 年初再次回归。1759 年 3 月这颗彗星如期通过了近日点,它最近一次回归是 1986 年,它的下次回归将在2061 年左右。
五 、预言哈雷彗星回归
两
条
基
本
思
路
1、重力等于万有引力
2、万有引力提供向心力
课堂小结
谢谢观看
THANK YOU!
“给我一个支点,我可以撬动地球。”
那给我们一个天平是否就可以称量地球的质量了呢?
不能
如果有人说他能称出地球的质量,你信吗?
我可以
天平 or 杆秤
卡文迪什
第七章 万有引力与宇宙航行
7.3 万有引力理论的成就
M=
若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的引力
卡文迪什
被称为能称出地球质量的人
GM=gR2
一、“称量”地球的质量
黄金代换公式
例题1:地球的质量到底有多大?已知:地球表面g=9.8m/s2,地球半径R=6400km,引力常量G=6.67×10-11Nm2/kg2。请你根据这些数据计算地球的质量。
M=6.0×1024kg
M=
如果测出了某行星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?
思考:应用万有引力可算出地球的质量,能否算出太阳的质量呢?
1.地球公转实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
近似
二、计算天体的质量
思考:地球作匀速圆周运动的向心力是由什么力来提供的?
r
M
m
F
地球作圆周运动的向心力是由太阳对地球的万有引力来提供的。
二、计算天体的质量
【注意】行星绕太阳做匀速圆周运动,向心力是由它们之间的万有引力提供的,即Fn=F万
二、计算天体的质量
r
M
m
F
地球公转角速度ω 不能直接测出,但我们知道地球公转的周期 T
(M与m无关)
二、计算天体的质量
天体球心之间距离
圆周运动半径
中心天体M
环绕天体m
求解思路:
环行天体的向心力由中心天体对其万有引力独家提供
具体方法:
二、计算天体的质量
注意:只能求解中心天体质量
中心天体M
环绕天体m
二、计算天体的质量
注意:只能求解中心天体质量
思考:如何求解环绕天体质量?
把环绕天体变成中心天体
思考:如何把环绕天体变成中心天体?
发射一颗卫星绕其运动测出卫星周期T、转动半径r即可。
拓展:利用月球求地球质量
月球绕地球运行的周期T=27.3天,月球与地球的平均距离r=3.84×108m
M地=5.98×1024kg
二、计算天体的质量
已知太阳与地球间的平均距离约为1.5x1011m,你能估算太阳的质量吗?换用其他行星的相关数据进行估算,结果会相近吗?为什么?
解:地球绕太阳运转的周期:
T=365×24×60×60s=3.15×107s
地球绕太阳做匀速圆周运动的向心力由万有引力提供,
虽然不同行星与太阳间的距离r和绕太阳公转的周期T 各不相同,但是根据开普勒第三定律,所有行星的 均相同,所以无论选择哪颗行星的轨道半径和公转周期进行计算,所得的太阳质量均相同。
已知引力常量G、月球中心到地球中心的距离r和月球绕地球运行的
周期T。仅利用这三个数据,可以估算出的物理量有( )
A.月球的质量 B.地球的质量
C.地球的半径 D.月球绕地球运行速度的大小
BD
【针对训练】
天体质量和密度的两种思路
1.重力加速度法:在天体表面,重力近似等于万有引力
M=
三、计算天体的密度
天体的体积:
2.环绕法:万有引力提供向心力F引=Fn
①已知环绕天体运动的轨道半径r、速度V、引力常量G,中心天体半径R
三、计算天体的密度
注意:r为环绕天体运动的轨道半径,R为中心天体的半径
2.环绕法:
①已知环绕天体运动的轨道半径r、速度V、引力常量G,中心天体半径R
三、计算天体的密度
②已知环绕天体运动的轨道半径r、角速度ω、引力常量G,中心天体半径R
③已知环绕天体运动的轨道半径r、周期T、引力常量G,中心天体半径R
④已知环绕天体运动的速度v、周期T、引力常量G,中心天体半径R
如何列式求解?
2.环绕法:
②已知环绕天体运动的轨道半径r、角速度ω、引力常量G,中心天体半径R
三、计算天体的密度
注意:r为环绕天体运动的轨道半径,R为中心天体的半径
2.环绕法:
③已知环绕天体运动的轨道半径r、周期T、引力常量G,中心天体半径R
注意:r为环绕天体运动的轨道半径,R为中心天体的半径
三、计算天体的密度
2.环绕法:
④已知环绕天体运动的速度v、周期T、引力常量G,中心天体半径R
注意:R为中心天体的半径
三、计算天体的密度
思考:如何求解r?
?
重力加速度法
环绕法
情景
已知天体(如地球)的半径R和天体(如地球)表面的重力加速度g
行星或卫星绕中心
天体做匀速圆周运动
思路
物体在表面的重力近似等于天体(如地球)与物体间的万有引力:
行星或卫星受到的万有引力充当向心力:
天体质量
天体(如地球)质量:
中心天体质量:
天体密度
?
?
说明
g为天体表面重力加速度,未知星球表面重力加速度通常利用实验测出,例如让小球做自由落体、平抛、上抛等运动
这种方法只能求中心天体质量,不能求卫星质量,T为公转周期r为轨道半径
R为中心天体半径
【针对训练】
宇航员为测量某一星球的质量,在该星球表面用弹簧测力计称得质量为m的物体,弹簧测力计示数为F,已知星球半径为R,引力常量为G,不考虑星球自转,求该星球质量M?
F引=G?
忽略星球自转
【针对训练】
课本P58面第1题
到了 18 世纪,人们已经知道太阳系有 7 颗行星,其中1781 年发现的第七颗行星 —— 天王星的运动轨道有些“古怪”:根据万有引力定律计算出来的轨道与实际观测的结果总有一些偏差。
?是天文观测数据不准确?
?是万有引力定律的准确性有问题?
?是天王星轨道外面还有一颗未发现的行星?
四、发现未知天体
英国剑桥大学的学生亚当斯和法国年轻的天文学家勒维耶相信未知行星的存在。他们根据天王星的观测资料,各自独立地利用万有引力定律计算出这颗“新”行星的轨道。1846 年 9 月 23 日晚,德国的伽勒在勒维耶预言的位置附近发现了这颗行星,人们称其为“笔尖下发现的行星”。后来,这颗行星被命名为海王星(图 7.3-2)。海王星的发现过程充分显示了理论对于实践的巨大指导作用,所用的“计算预测和观察”的方法指导人们寻找新的天体。
理论轨道
实际轨道
海王星发现之后,人们发现它的轨道也与理论计算的不一致。于是几位学者用亚当斯和勒维耶列的方法预言另一颗行星的存在。
在预言提出之后,1930年3月14日,汤博发现了这颗行
星——冥王星。
哈雷依据万有引力定律,用一年时间计算了它们的轨道。发现 1531 年、1607 年和 1682 年出现的这三颗彗星轨道看起来如出一辙,他大胆预言,这三次出现的彗星是同一颗星(图 7.3-3),周期约为 76 年,并预言它将于 1758 年底或 1759 年初再次回归。1759 年 3 月这颗彗星如期通过了近日点,它最近一次回归是 1986 年,它的下次回归将在2061 年左右。
五 、预言哈雷彗星回归
两
条
基
本
思
路
1、重力等于万有引力
2、万有引力提供向心力
课堂小结
谢谢观看
THANK YOU!
